ESE 680 Lecture 2 01112007 ESE 680 Special

ESE 680 Lecture 2 01/11/2007 ESE 680 Special topics in ESE Distributed Dynamical Systems Ali Jadbabaie Department of Electrical and Systems Engineering and GRASP Laboratory University of Pennsylvania 365 GRW jadbabai@seas. upenn. edu http: //www. seas. upenn. edu/~jadbabai/ESE 680/ese 680. html A. Jadbabaie “ESE 680: Distributed Dynamical systems”

Course Info This is a RESEARCH SEMINAR Requires a lot of INDEPENDENT, critical reading of literature You are expected to actively PARTICIPATE in discussions A LOT of reading is required and you need to be able to present papers There are very few didactic lectures Here is a brief summary of last time A. Jadbabaie “ESE 680: Distributed Dynamical systems”

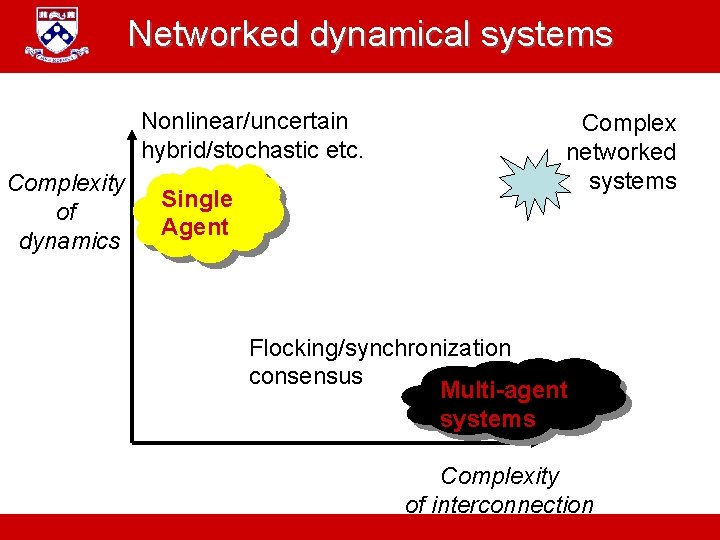
Networked dynamical systems Nonlinear/uncertain hybrid/stochastic etc. Complexity of dynamics Single Agent Complex networked systems Flocking/synchronization consensus Multi-agent systems Complexity of interconnection A. Jadbabaie “ESE 680: Distributed Dynamical systems”

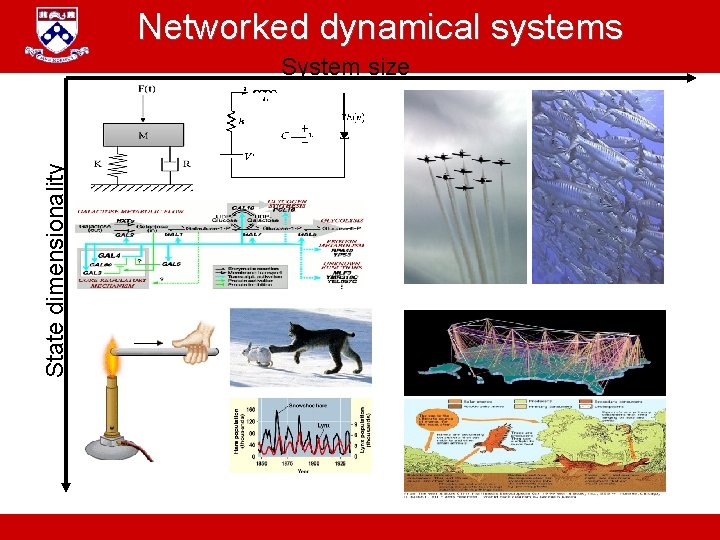
Networked dynamical systems State dimensionality System size A. Jadbabaie “ESE 680: Distributed Dynamical systems”

Statistical Physics and emergence of collective behavior f t u b s e r u t c e onj c d n sa n o i t ula Sim A. Jadbabaie “ESE 680: Distributed Dynamical systems” p “ ew ’ s f roo

p “ ew ’ s f o o r i k r o W f t u b s m ste y s ng A. Jadbabaie “ESE 680: Distributed Dynamical systems”

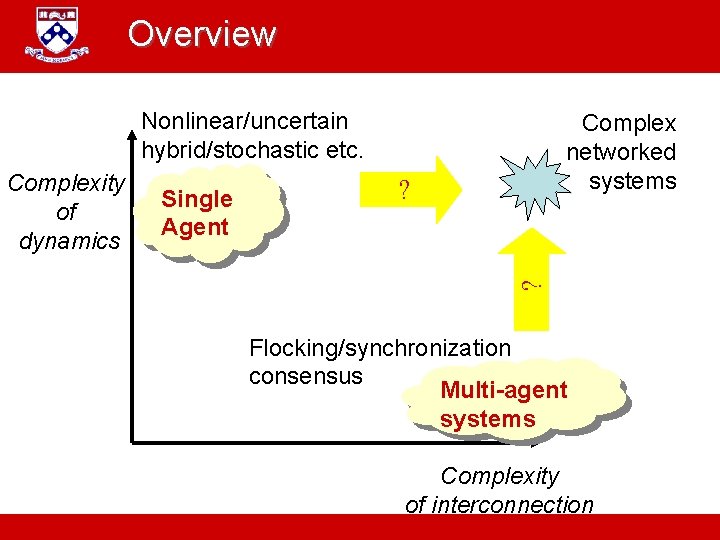
Overview Nonlinear/uncertain hybrid/stochastic etc. ? Single Agent ? Complexity of dynamics Complex networked systems Flocking/synchronization consensus Multi-agent systems Complexity of interconnection A. Jadbabaie “ESE 680: Distributed Dynamical systems”

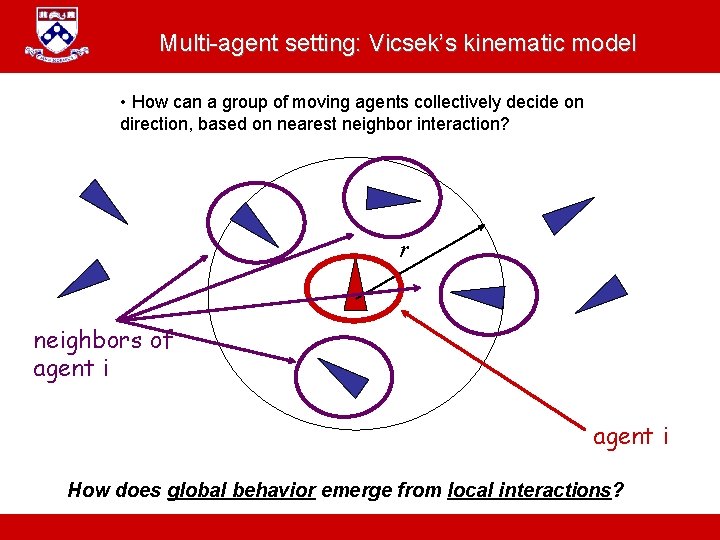
Multi-agent setting: Vicsek’s kinematic model • How can a group of moving agents collectively decide on direction, based on nearest neighbor interaction? r neighbors of agent i How does global behavior emerge from local interactions? A. Jadbabaie “ESE 680: Distributed Dynamical systems”

Synchronization Fireflies Flashing From D. Attenborough “Trials of Life – Talking to strangers” A. Jadbabaie “ESE 680: Distributed Dynamical systems”

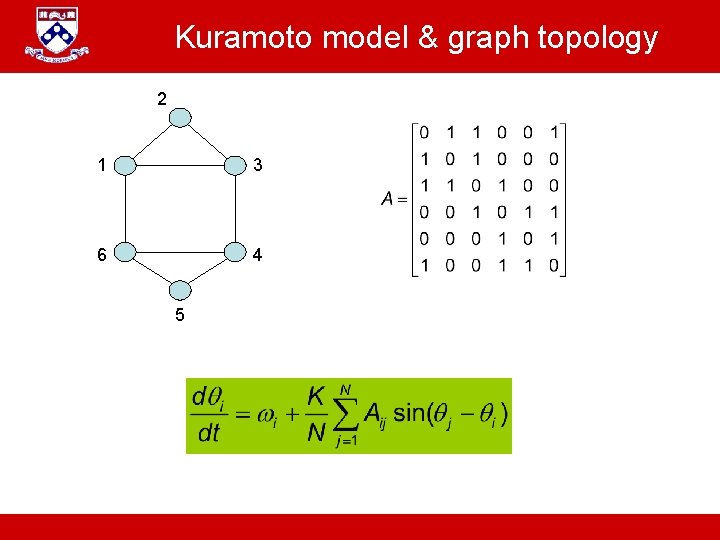
Kuramoto Model All-to-all interaction This is the Kuramoto model We assume throughout homogeneous coupling. A. Jadbabaie “ESE 680: Distributed Dynamical systems”

Kuramoto model & graph topology 2 1 3 6 4 5 A. Jadbabaie “ESE 680: Distributed Dynamical systems”

Ubiquity of Dual Decompositions Dual Decomposition is THE key idea that makes the internet protocols “work” in a distributed asynchronous fashion What is the connection between flocking, oscillator synchronization, and the internet? But, how DO “these internets” work? Senator Ted Stevens (R-Alaska), (the architect of the 280 million dollar bridge to nowhere: “ …and again, the Internet is not something you just dump something on. It's not a big truck. It's a series of tubes. And if you don't understand those tubes can be filled and if they are filled, when you put your message in, it gets in line and it's going to be delayed by anyone that puts into that tube enormous amounts of material, enormous amounts of material. ” A. Jadbabaie “ESE 680: Distributed Dynamical systems”

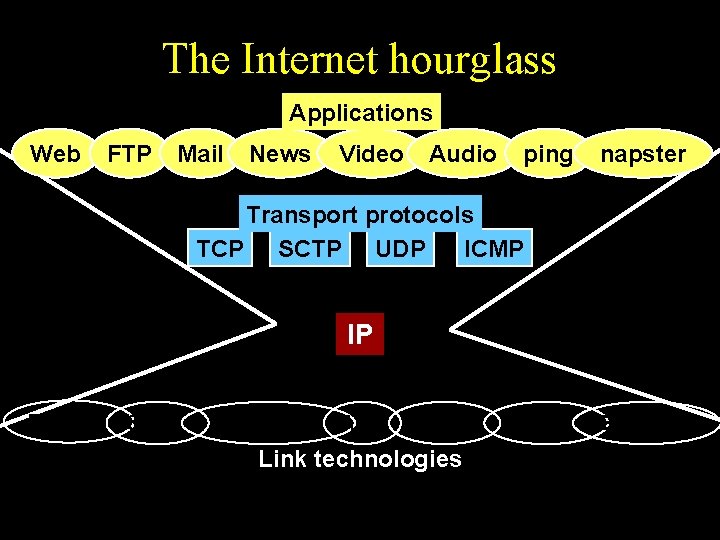
The Internet hourglass Applications Web FTP Mail News Video Audio ping napster Transport protocols TCP SCTP UDP ICMP IP Ethernet 802. 11 Power lines ATM Optical Link technologies Satellite Bluetooth

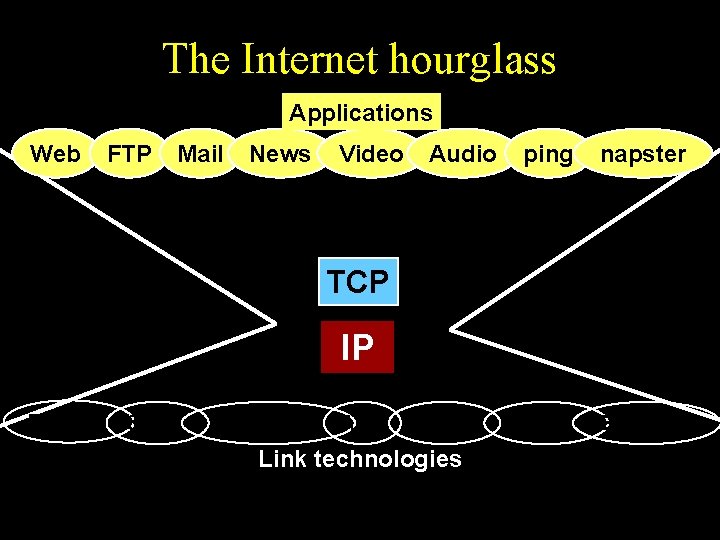
The Internet hourglass Applications Web FTP Mail News Video Audio ping napster TCP IP Ethernet 802. 11 Power lines ATM Optical Link technologies Satellite Bluetooth

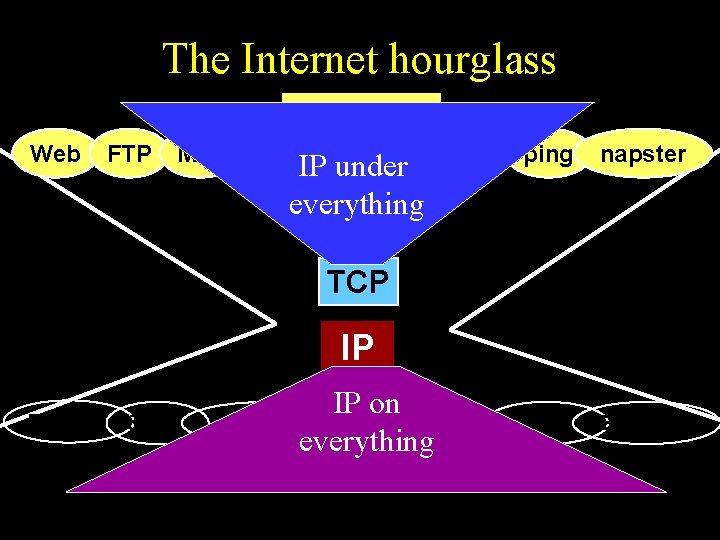
The Internet hourglass Applications Web FTP Mail News Video Audio IP under everything ping napster TCP IP Ethernet 802. 11 IP on Power lines ATM Optical everything Link technologies Satellite Bluetooth

Congestion Control for the Internet Aims to avoid congestion collapse • Congestion collapse appeared in the late 80’s because of the lack of congestion control • Intuitive congestion control design alleviated the problem… • Until a few years ago when it was shown to be unstable! New designs aim to achieve: • Optimal sharing of available resources at equilibrium; • Scalable stability for • arbitrary topologies (size and connectivity) • arbitrary links’ capacities • arbitrary, inhomogeneous round trip times (time delays) Last property has been proven only for the linearized system – here we provide a proof for the nonlinear case A. Jadbabaie “ESE 680: Distributed Dynamical systems”

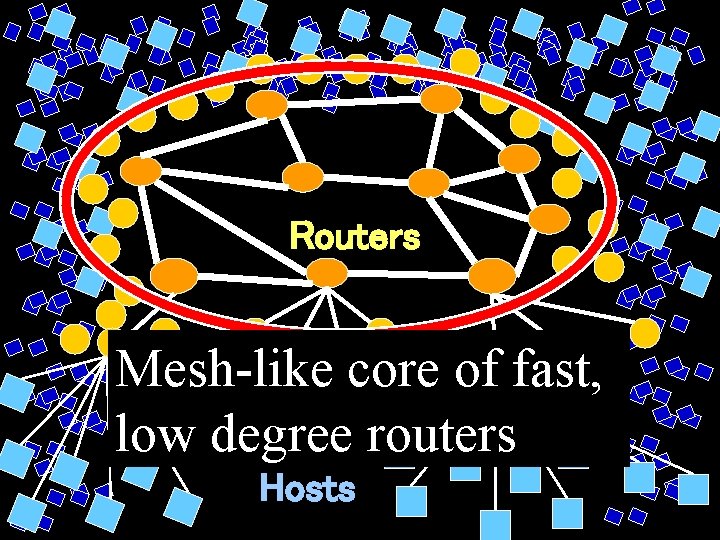
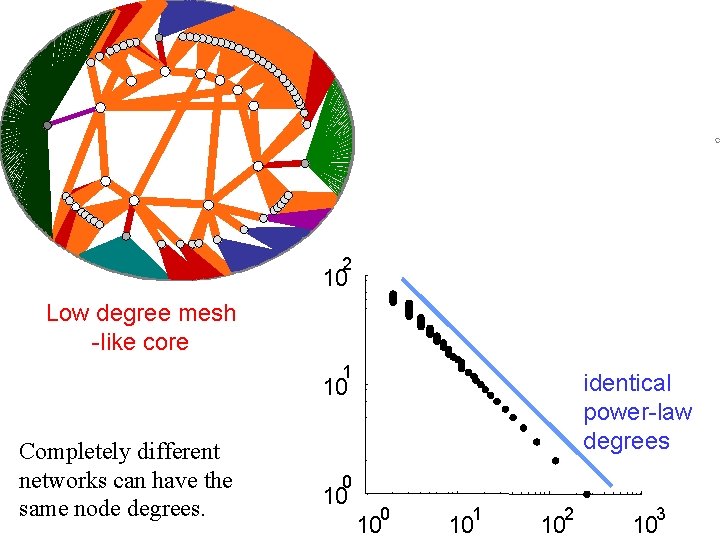
Routers Mesh-like core of fast, low degree routers Hosts

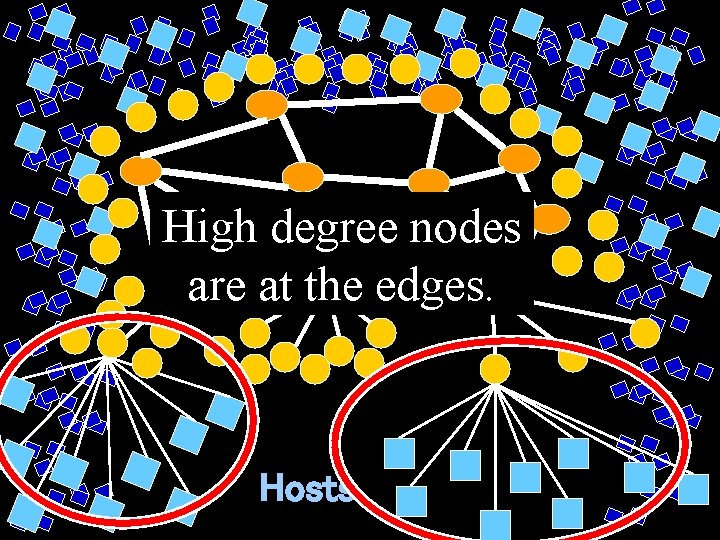
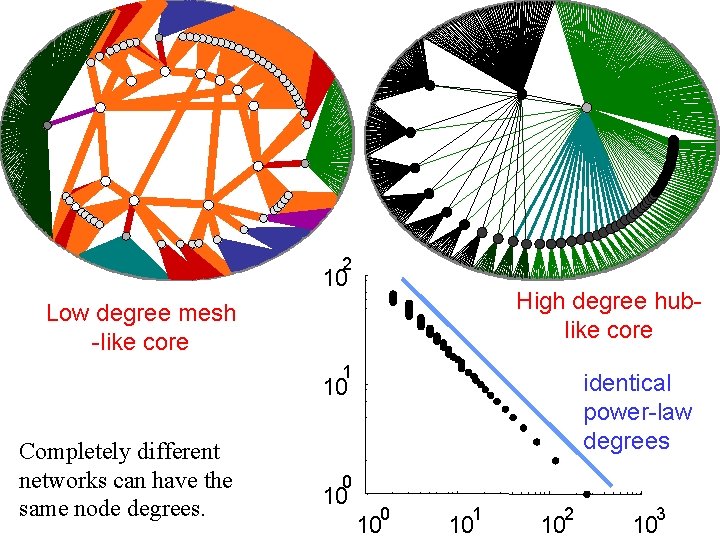
High degree Routersnodes are at the edges. Hosts

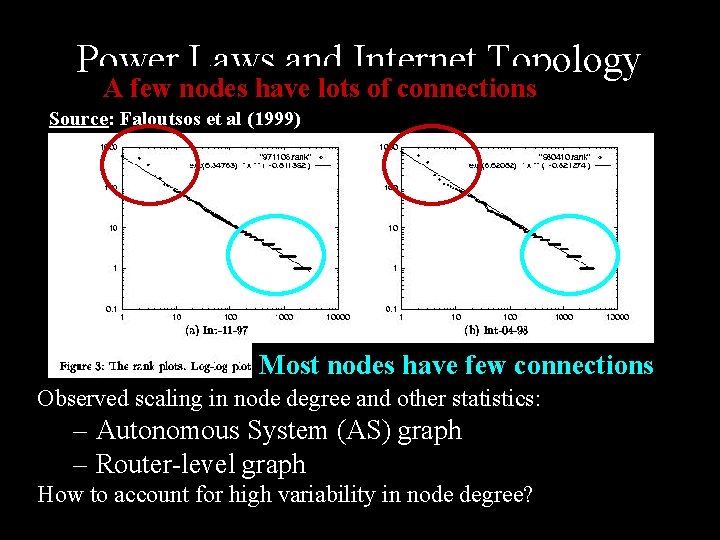
Power Laws and Internet Topology A few nodes have lots of connections number of connections Source: Faloutsos et al (1999) rank Most nodes have few connections Observed scaling in node degree and other statistics: – Autonomous System (AS) graph – Router-level graph How to account for high variability in node degree?

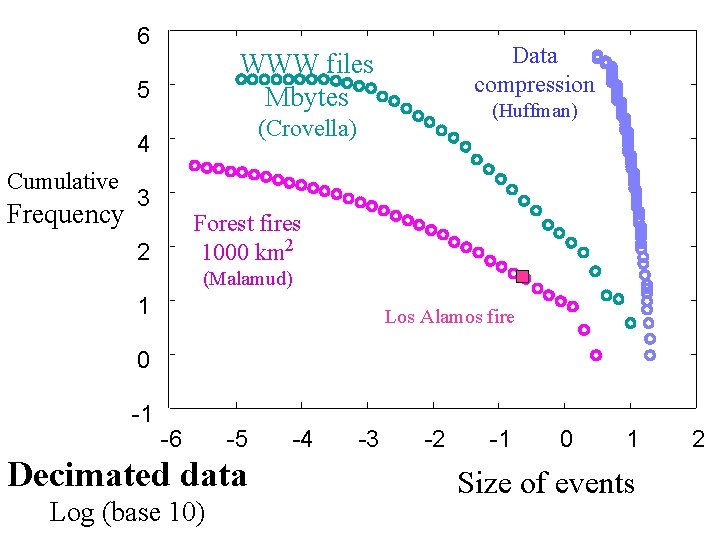
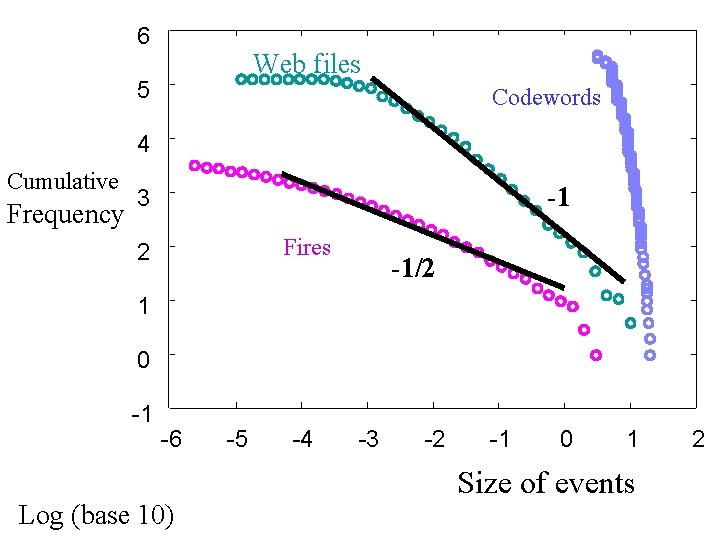
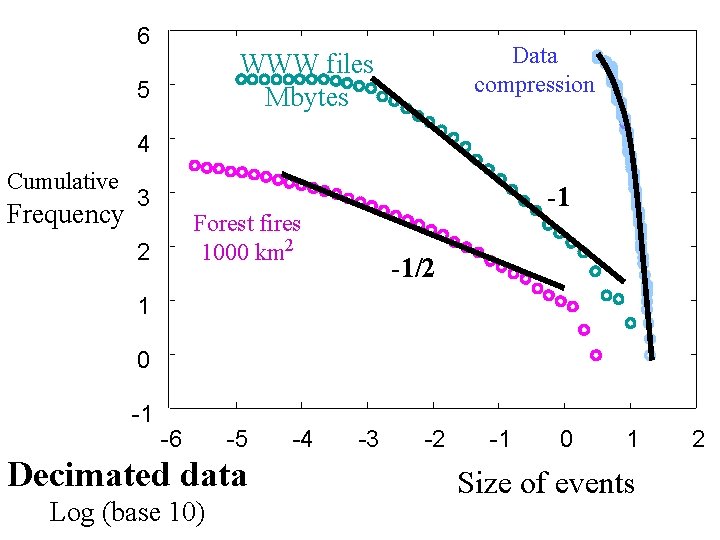
6 5 Frequency (Huffman) (Crovella) 4 Cumulative Data compression WWW files Mbytes 3 Forest fires 1000 km 2 2 (Malamud) 1 Los Alamos fire 0 -1 -6 -5 Decimated data Log (base 10) -4 -3 -2 -1 0 1 Size of events 2

18 Sep 1998 Forest Fires: An Example of Self-Organized Critical Behavior Bruce D. Malamud, Gleb Morein, Donald L. Turcotte 4 data sets

6 Web files 5 Codewords 4 Cumulative Frequency -1 3 Fires 2 -1/2 1 0 -1 -6 Log (base 10) -5 -4 -3 -2 -1 0 1 Size of events 2

>1 e 5 6 files Data compression WWW files Mbytes 5 (Huffman) (Crovella) >4 e 3 fires 4 Cumulative 3 Frequency Forest fires 1000 km 2 2 (Malamud) 1 Los Alamos fire 0 -1 -6 -5 Decimated data Log (base 10) -4 -3 -2 -1 0 1 Size of events 2

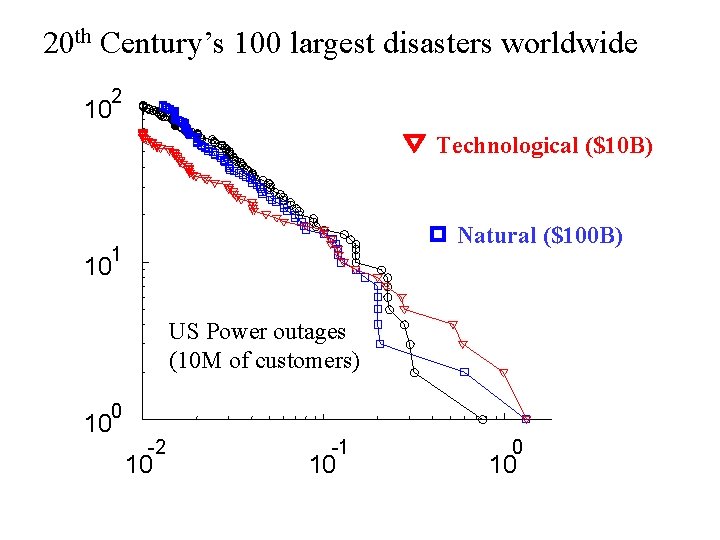
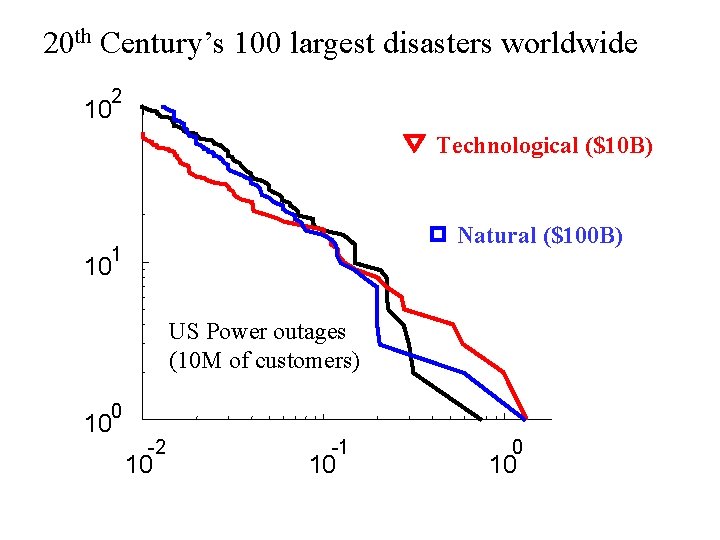
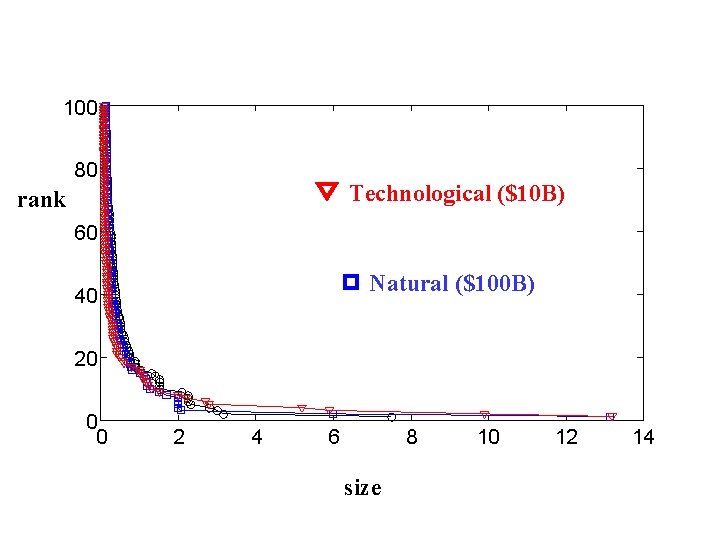
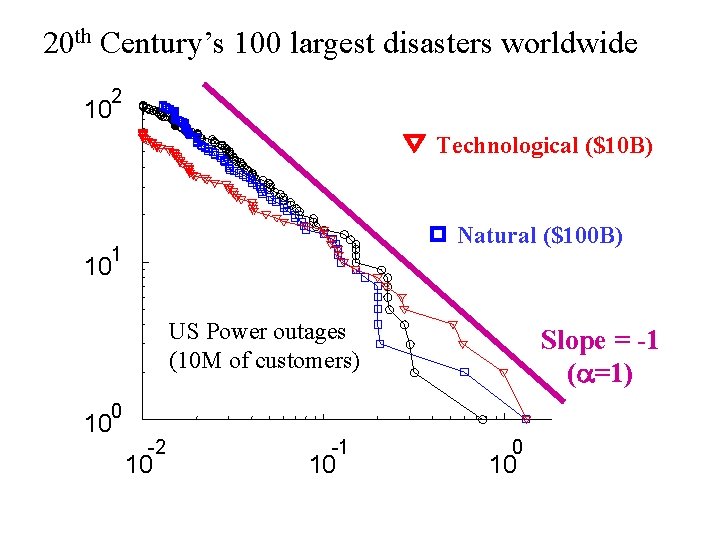
20 th Century’s 100 largest disasters worldwide 2 10 Technological ($10 B) Natural ($100 B) 1 10 US Power outages (10 M of customers) 0 10 -2 10 -1 10 0 10

20 th Century’s 100 largest disasters worldwide 2 10 Technological ($10 B) Natural ($100 B) 1 10 US Power outages (10 M of customers) 0 10 -2 10 -1 10 0 10

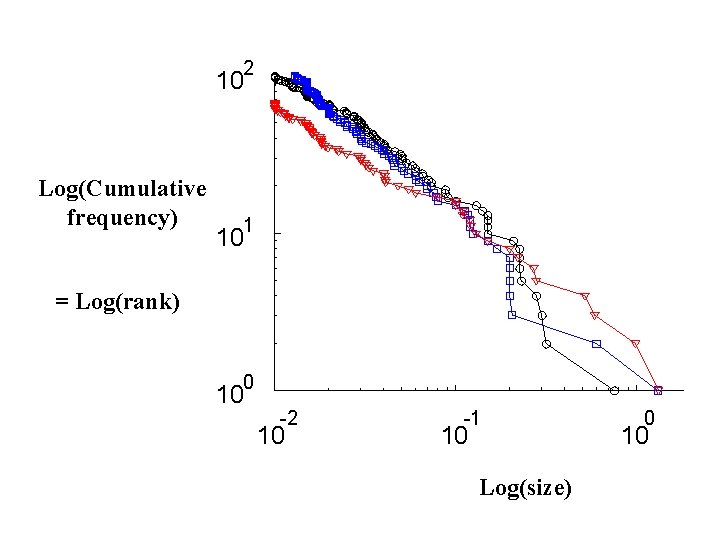
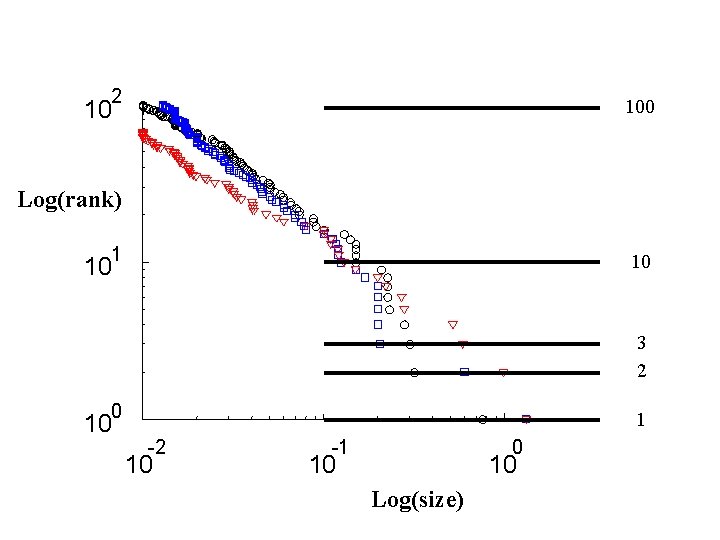
2 10 Log(Cumulative frequency) 1 10 = Log(rank) 0 10 -2 10 -1 10 Log(size) 0 10

100 80 Technological ($10 B) rank 60 Natural ($100 B) 40 20 0 0 2 4 6 8 size 10 12 14

2 10 100 Log(rank) 1 10 10 3 2 0 10 1 -2 10 -1 0 10 10 Log(size)

20 th Century’s 100 largest disasters worldwide 2 10 Technological ($10 B) Natural ($100 B) 1 10 US Power outages (10 M of customers) Slope = -1 ( =1) 0 10 -2 10 -1 10 0 10

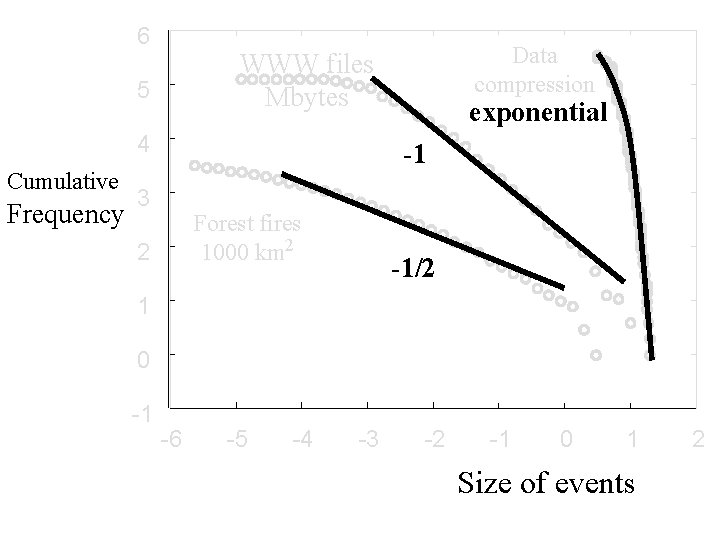
6 Data compression WWW files Mbytes 5 4 Cumulative Frequency 3 -1 Forest fires 1000 km 2 2 -1/2 1 0 -1 -6 -5 Decimated data Log (base 10) -4 -3 -2 -1 0 1 Size of events 2

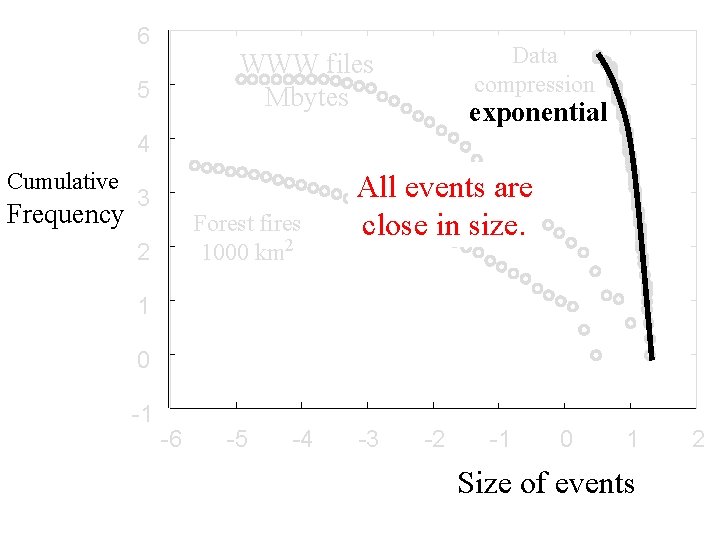
6 5 4 Cumulative Frequency Data compression WWW files Mbytes exponential -1 3 Forest fires 1000 km 2 2 -1/2 1 0 -1 -6 -5 -4 -3 -2 -1 0 1 Size of events 2

6 Data compression WWW files Mbytes 5 exponential 4 Cumulative Frequency 3 Forest fires 1000 km 2 2 All events are close in size. 1 0 -1 -6 -5 -4 -3 -2 -1 0 1 Size of events 2

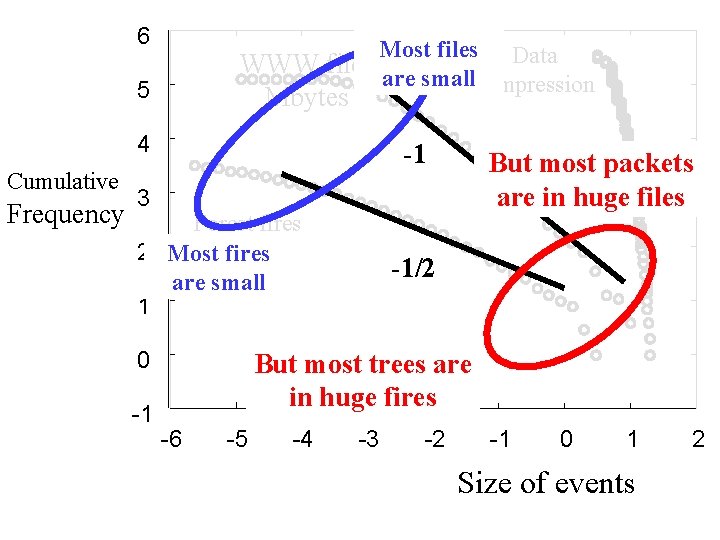
6 5 4 Cumulative Frequency Data compression WWW files Mbytes -1 3 Forest fires 1000 km 2 Most 2 events are small 1 0 -1 -1/2 But the large events are huge -6 -5 -4 -3 -2 -1 0 1 Size of events 2

6 Cumulative Frequency 5 Most files Data WWW files are small compression 4 -1 Mbytes But most packets are in huge files 3 Forest fires 1000 km 2 2 Most fires are small 1 0 -1 -1/2 But most trees are in huge fires -6 -5 -4 -3 -2 -1 0 1 Size of events 2

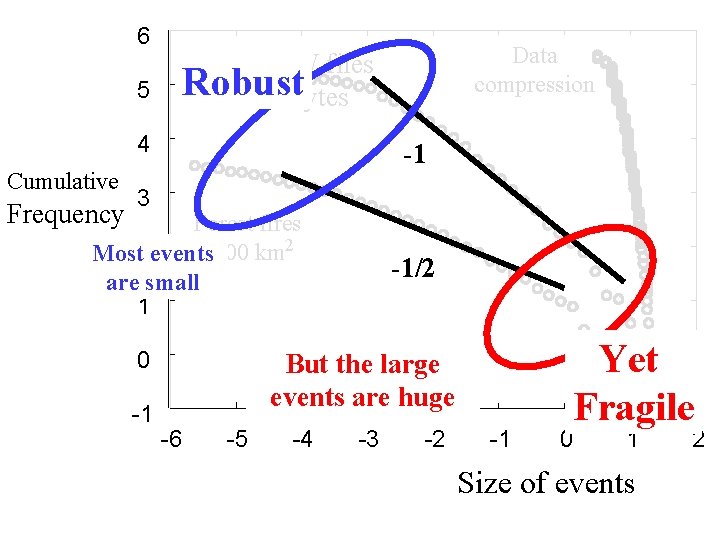
6 5 4 Cumulative Frequency Data compression WWW files Robust Mbytes -1 3 Forest fires 1000 km 2 Most 2 events are small 1 0 -1 -1/2 But the large events are huge -6 -5 -4 -3 -2 -1 Yet Fragile 0 1 Size of events 2

Large scale phenomena is extremely non -Gaussian • The microscopic world is largely exponential • The laboratory world is largely Gaussian because of the central limit theorem • The large scale phenomena has heavy tails (fat tails) and power laws

Power Laws in Topology Modeling • Recent emphasis has been on whether or not a given topology model/generator can reproduce the same types of macroscopic statistics, especially power law-type degree distributions • Lots of degree-based models have been proposed – All of them are based on random graphs, usually with some form of preferential attachment

Models of Internet Topology • These topology models are merely descriptive – Measure some feature of interest (connectivity) – Develop a model that replicates that feature – Make claims about the similarity between the real system and the model – A type of “curve fitting”? • Unfortunately, by focusing exclusively on node degree distribution, these models that get the story wrong • We seek something that is explanatory – Consistent with the drivers of topology design and deployment – Consistent with the engineering-related details

Heuristically Optimal Network Mesh-like core of fast, Coresrouters low degree High degree Edges nodes are at the edges. Hosts

Abilene Backbone Physical Connectivity (as of December 16, 2003) Intermountain Giga. Po. P Front Range Giga. Po. P Arizona St. Oregon Giga. Po. P Internet routerlevel topology U. Memphis Indiana Giga. Po. P Pacific Northwest Giga. Po. P U. Louisville Great Plains OARNET Star. Light MREN NYSERNet Kansas Denver City UNM WPI Indianapolis Chicago Seattle U. Hawaii GEANT Sunnyvale SURFNet Rutgers U. Wash D. C. Los Angeles Uni. Net Trans. PAC/APAN MANLAN Houston North Texas Giga. Po. P Texas Tech SOX Miss State Giga. Po. P UT Austin UT-SW Med Ctr. Atlanta SFGP/ AMPATH Texas Giga. Po P La. Net Tulane U. Northern Crossroads SINet New York ESnet AMES NGIX WIDE Wisc. REN NCSA Iowa St. CENIC 0. 1 -0. 5 Gbps 0. 5 -1. 0 Gbps 1. 0 -5. 0 Gbps 5. 0 -10. 0 Gbps Merit One. Net Qwest Labs U. Arizona Pacific Wave Northern Lights Florida A&M U. So. Florida MAGPI PSC DARPA Boss. Net UMD NGIX U. Florida NCNI/MCNC Mid-Atlantic Crossroads Drexel U. U. Delaware

2 10 Low degree mesh -like core 1 identical power-law degrees 10 Completely different networks can have the same node degrees. 0 10 1 10 2 10 3 10

2 10 High degree hublike core Low degree mesh -like core 1 identical power-law degrees 10 Completely different networks can have the same node degrees. 0 10 1 10 2 10 3 10

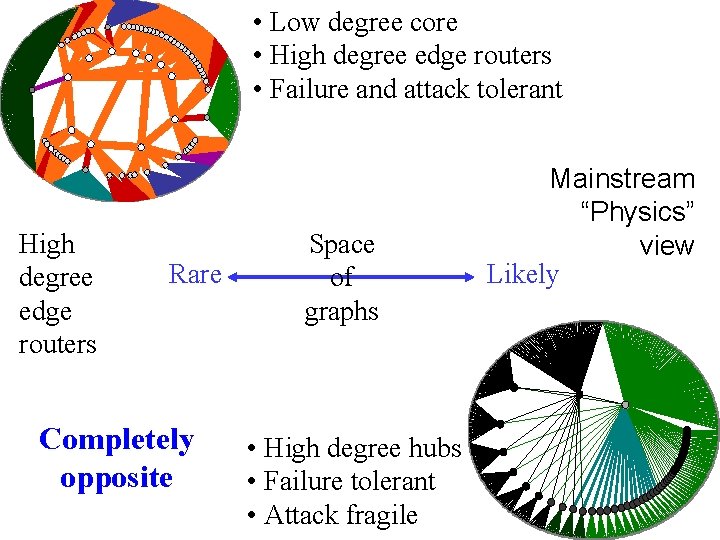
• Low degree core • High degree edge routers • Failure and attack tolerant High degree edge routers Rare Completely opposite Space of graphs • High degree hubs • Failure tolerant • Attack fragile Mainstream “Physics” view Likely

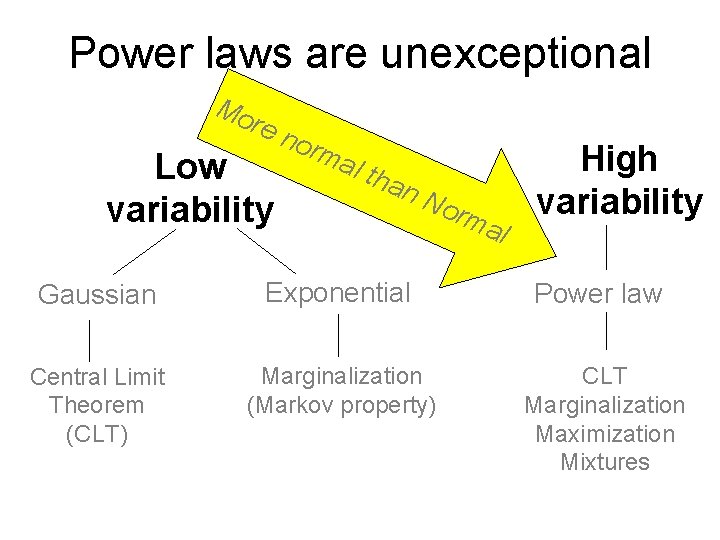
Power laws are ubiquitous, not. M just the internet ore Low variability nor ma l th an No rma l High variability Gaussian Exponential Power law Central Limit Theorem (CLT) Marginalization (Markov property) CLT Marginalization Maximization Mixtures

Power laws are unexceptional Mo re n Low variability orm al t han No rma l High variability Gaussian Exponential Power law Central Limit Theorem (CLT) Marginalization (Markov property) CLT Marginalization Maximization Mixtures

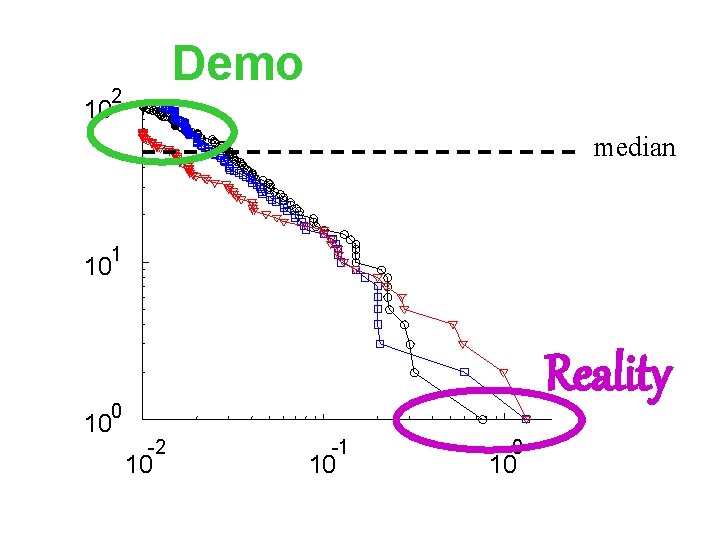
Demo 2 10 median 1 10 Reality 0 10 -2 10 -1 10 0 10

2 Robust 10 median 1 10 0 10 -2 10 -1 10 0 10 Yet Fragile

Lessons learnt • You cant just analyze graphs of complex networks without domain knowledge. A network is much more than a graph. • Degree distributions DO NOT tell us everything • Need to couple GRAPH with DYNAMICS • This is the essential message of the course

Course Road Map Theme is dynamics+ graph theory Tentative flow of presentations: Linear algebra of non-negative matrices and basics of graph theory Markov chains and Perron Frobenius Theory Graph Laplacians Synchronization, agreement and consensus control theory and robotics Networking Physics Complex networks, power laws Kleinberg’s model, Barabassi’s preferential attachment Newman’s survey papers Small world networks, Watts Strogatz Model Google’s Page. Rank Reaction rate equations, metabolic networks, systems biology Internet, degree distributions, internet topology Random graph models Dual decomposition theory Beyond graphs Simplicial complexes and algebraic topology Coverage problems Distributed optimal control A. Jadbabaie “ESE 680: Distributed Dynamical systems”

Need volunteers for each section We have about 12 weeks, 24 sessions, we could read about 18 -20 papers A. Jadbabaie “ESE 680: Distributed Dynamical systems”

Beyond Graphs in Networked Systems Main Idea: understanding global properties with local information: algebraic topology For certain problems, e. g. coverage, makes sense to go beyond graphs and pair-wise interactions Example: Given a set of sensor nodes in a given domain (possibly bounded by a fence), is every point of the domain under surveillance by at least one node? A. Jadbabaie “ESE 680: Distributed Dynamical systems”

Coverage Problems Problem: Given a set of sensor nodes in a domain (possibly bounded by a fence), is every point of the domain under surveillance by at least one node? A. Jadbabaie “ESE 680: Distributed Dynamical systems”

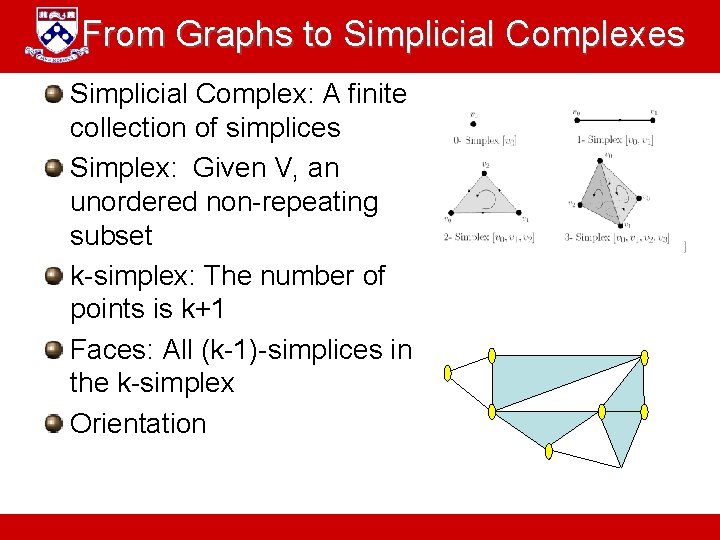
From Graphs to Simplicial Complexes Simplicial Complex: A finite collection of simplices Simplex: Given V, an unordered non-repeating subset k-simplex: The number of points is k+1 Faces: All (k-1)-simplices in the k-simplex Orientation A. Jadbabaie “ESE 680: Distributed Dynamical systems”

From Graphs to Simplicial Complexes Simplicial complex: made up of simplices of several dimensions Properties Whenever a simplex lies in the collection then so does each of its faces Whenever two simplices intersect, they do so in a common face. Valid Examples Graphs Triangulations Invalid examples A. Jadbabaie “ESE 680: Distributed Dynamical systems”

Rips-Vietoris Simplicial Complex 0 -simplices : Nodes 1 -simplices : Edges 2 -simplices: A triangle in the connectivity graph ~ 2 simplex (Fill in with a face) K-simplices: a complete subgraph on k+1 vertices k-simplex in the Rips complex ~ (k+1) points within communication range of each other A. Jadbabaie “ESE 680: Distributed Dynamical systems” Generalization of r-disk graphs

Rips and Čech Complexes: Topological vs. Geometric information A set of points • (Rips complex of radius distance between k points are less than. ): k-simplex, if the pairwise - Easy to compute in a dsitributed manner. - However, Does not preserve the topological properties. • (Čech complex of radius ): k-simplex, if k coverage disks of radius overlap - Hard to compute. - Preserves the topological properties. A. Jadbabaie “ESE 680: Distributed Dynamical systems”

Coverage Problems Intersection of sensing ~ simplicial complexes Communication graphs ~ simplicial complexes Holes ~ homology of simplicial complexes A sensor network has coverage hole if there is a “robust” hole in the simplicial complexes induced by the communication graphs [Ghrist et al. ] A. Jadbabaie “ESE 680: Distributed Dynamical systems”

Relevance of Homology dim H 0(X) ~ no of connected components of X dim H 1(X) ~ types of loops in X that surround ‘punctures’ dim Hk(X) ~ no of k+1 -dimensional ‘voids’ in X Available software Plex (Stanford) CHom. P (Georgia Tech) A. Jadbabaie “ESE 680: Distributed Dynamical systems”

Combinatorial k-Laplacians Since X is finite we can represent the boundary maps in matrix form Moreover, we can get the adjoint incidence matrix [Eckmann 1945] The Combinatorial k-Laplacian is given by Note: A. Jadbabaie “ESE 680: Distributed Dynamical systems”

k-Laplacian at the Simplex Level Adjacency of a simplex to other simplices Upper adjacency if they share a higher simplex (e. g. 2 nodes connected by an edge) Lower adjacency if they share a common lower simplex (e. g. two edges share a node) ‘Local’ formula with orientations A. Jadbabaie “ESE 680: Distributed Dynamical systems”

k-Laplacian at the Simplex Level Adjacency of a simplex to other simplices Upper adjacency if they share a higher simplex (e. g. 2 nodes connected by an edge) Lower adjacency if they share a common lower simplex (e. g. two edges share a node) ‘Local’ formula with orientations Hodge theory, 1930’s: Kernel of the Laplacian ~ homologies A. Jadbabaie “ESE 680: Distributed Dynamical systems”

Laplacian Flows Laplacian flows : a semi-stable dynamical system (Recall heat equation for k = 0) [Muhammad-Egerstedt MTNS’ 06] System is asymptotically stable if and only if rank(Hk(X)) = 0. A method to detect ‘no holes’ locally A. Jadbabaie “ESE 680: Distributed Dynamical systems”

Laplacian Flows (contd. ) System converges to the unique harmonic cycle if rank(Hk(X)) = 1. A method to detect ‘proximity to hole’ locally when single hole When rank(Hk(X)) > 1 : System converges to the span of harmonic homology cycles A. Jadbabaie “ESE 680: Distributed Dynamical systems”

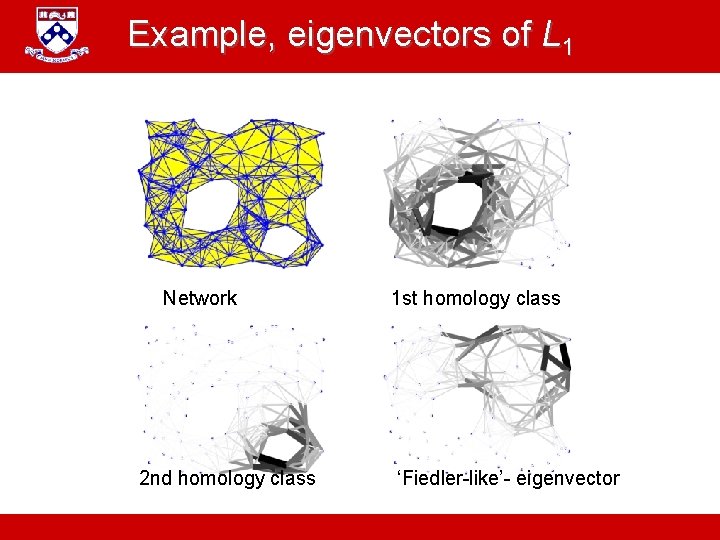
Example, eigenvectors of L 1 Network 2 nd homology class A. Jadbabaie “ESE 680: Distributed Dynamical systems” 1 st homology class ‘Fiedler-like’- eigenvector

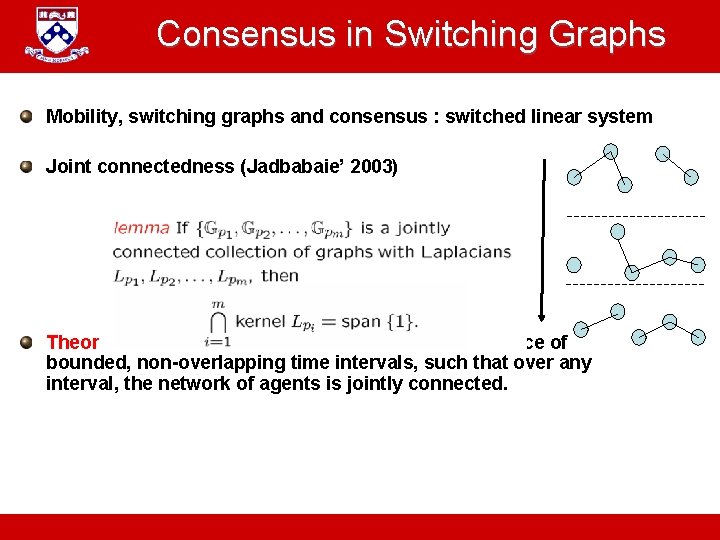
Consensus in Switching Graphs Mobility, switching graphs and consensus : switched linear system Joint connectedness (Jadbabaie’ 2003) Theorem : Consensus if and only if there is a sequence of bounded, non-overlapping time intervals, such that over any interval, the network of agents is jointly connected. A. Jadbabaie “ESE 680: Distributed Dynamical systems”

Coverage in Switching Simplicial Complexes Can we repeat similar analysis for switching simplicial complexes? YES! Jointly `hole-free’ simplicial complexes Joint hole-free implies trivial homology in union complex Theorem (Muhammad, Jadbabaie ’ 06): Switched linear system is globally asymptotically stable if and only if there exists an infinite sequence of bounded intervals, across each of which the simplicial complexes encountered are jointly hole-free. A. Jadbabaie “ESE 680: Distributed Dynamical systems”

Switching Simplicial Complexes: Random Switching times are from a Poisson point process with rate The complexes are drawn independently from a common distribution. [Salehi, Jadbabaie] The stochastic dynamical system is globally asymptotically stable if and only if A. Jadbabaie “ESE 680: Distributed Dynamical systems”

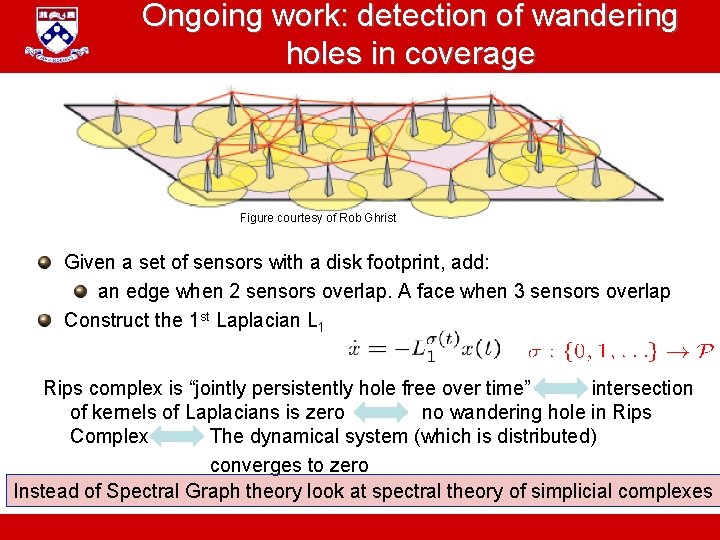
Ongoing work: detection of wandering holes in coverage Figure courtesy of Rob Ghrist Given a set of sensors with a disk footprint, add: an edge when 2 sensors overlap. A face when 3 sensors overlap Construct the 1 st Laplacian L 1 Rips complex is “jointly persistently hole free over time” intersection of kernels of Laplacians is zero no wandering hole in Rips The dynamical system (which is distributed) Complex converges to zero Instead of Spectral Graph theory look at spectral theory of simplicial complexes A. Jadbabaie “ESE 680: Distributed Dynamical systems”

Results on Spatially invariant systems and distributed control Mostly over highly symmetric graphs w/ identical dynamics Infinite Horizon Quadratic Cost No constraints on inputs and states A. Jadbabaie “ESE 680: Distributed Dynamical systems”

Structure of optimal control for spatially distributed systems: spatially invariant case Model of each subsystem: Does the optimal control policy have the same spatial structure as plant ? In other words, is it spatially distributed ? Finite Horizon Optimal Control problem: Finite Horizon Quadratic Cost A. Jadbabaie “ESE 680: Distributed Dynamical systems”

Identical dynamics over infinite lattices Fourier Analysis on Lattice: 1 D Lattice: Signals in the spatial domain: Fourier transform: For simplicity, replace Fourier transform: G : spatial domain A. Jadbabaie “ESE 680: Distributed Dynamical systems”

Translation Invariant Operators Definition: . Translation Operator: Q is translation invariant operator if Consider translation invariant operators of this form Example: Global cost function 1 D Lattice: agent k is coupled to its neighbors through cost function J in which A. Jadbabaie “ESE 680: Distributed Dynamical systems”

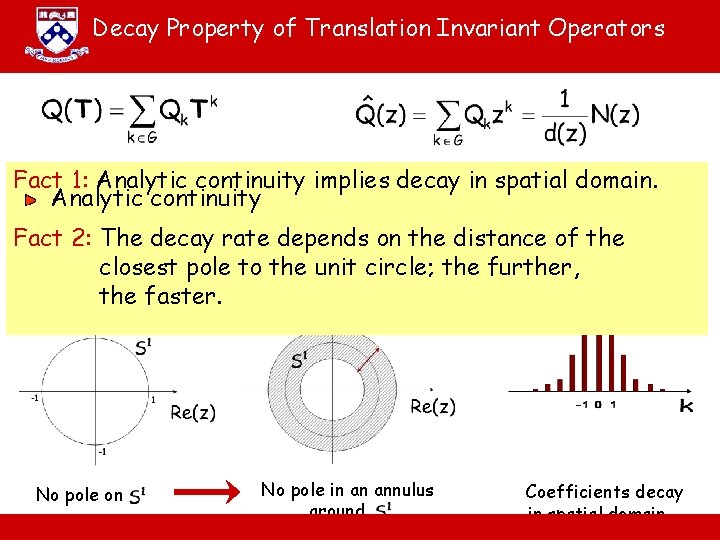
Decay Property of Translation Invariant Operators Fact 1: Analytic continuity implies decay in spatial domain. Analytic continuity Fact 2: The decay rate depends on the distance of the closest pole to the unit circle; the further, the faster. No pole on No pole in an annulus around A. Jadbabaie “ESE 680: Distributed Dynamical systems” Coefficients decay in spatial domain

Back to our problem Model of each subsystem: Notation: A. Jadbabaie “ESE 680: Distributed Dynamical systems”

Spatial Locality of Centralized RHC Finite Horizon Quadratic Cost: can be obtained from a parameterized family of DAREs: for all . is spatially decaying: A. Jadbabaie “ESE 680: Distributed Dynamical systems”

Spatial Locality of the Optimal Solution Theorem: Given the initial condition x(0), the optimal solutions are : (1) Affine maps of x(0), i. e. , (2) Spatially distributed, i. e. , A. Jadbabaie “ESE 680: Distributed Dynamical systems”

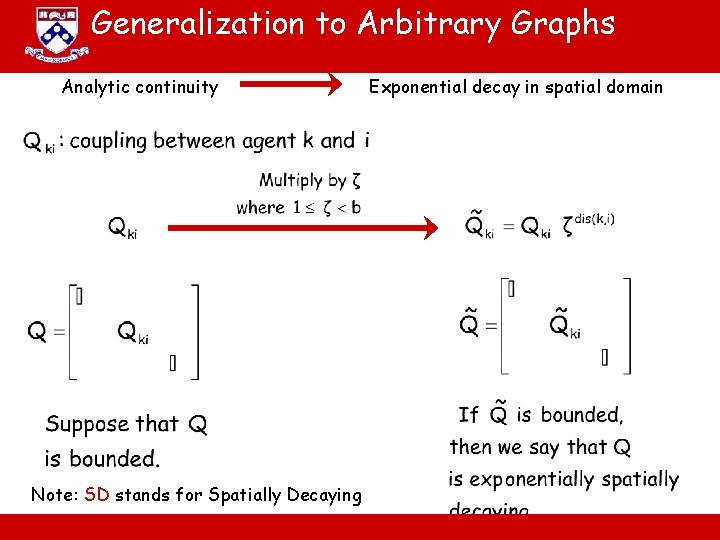
Generalization to Arbitrary Graphs Analytic continuity Note: SD stands for Spatially Decaying A. Jadbabaie “ESE 680: Distributed Dynamical systems” Exponential decay in spatial domain

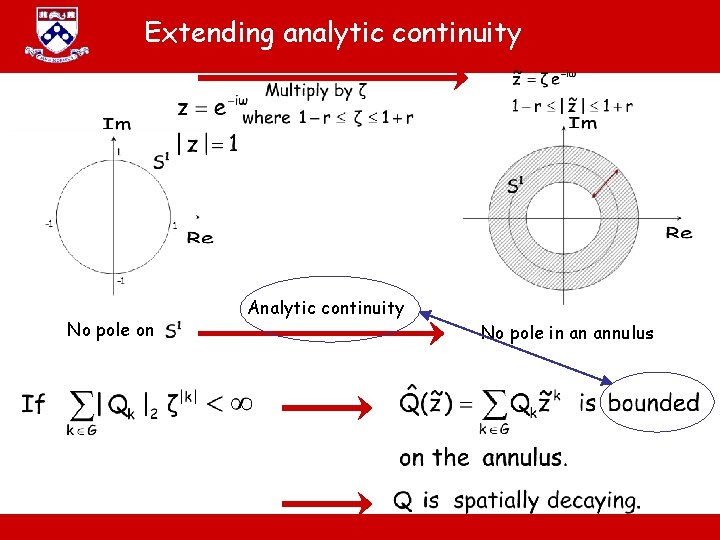
Extending analytic continuity No pole on Analytic continuity A. Jadbabaie “ESE 680: Distributed Dynamical systems” No pole in an annulus

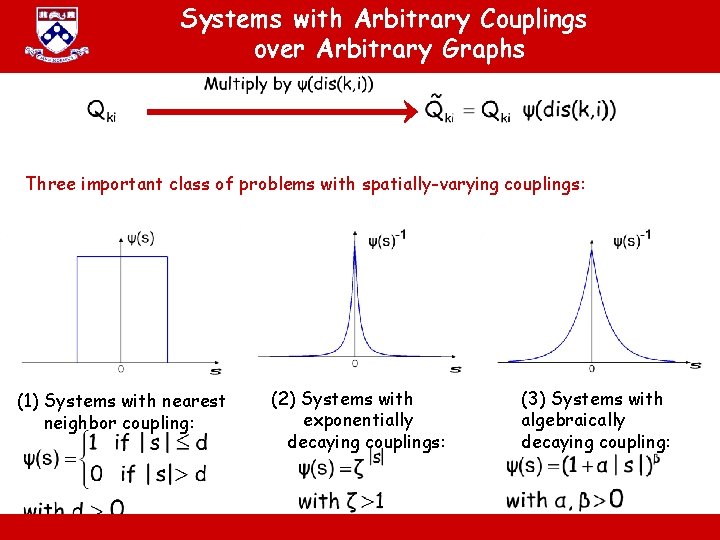
Systems with Arbitrary Couplings over Arbitrary Graphs Three important class of problems with spatially-varying couplings: (1) Systems with nearest neighbor coupling: (2) Systems with exponentially decaying couplings: A. Jadbabaie “ESE 680: Distributed Dynamical systems” (3) Systems with algebraically decaying coupling:

Properties of SD operators Definition: Theorem: sums, products and inverses of SD operators are SD. Therefore, if A and B, Q , and R are SD (1) Solution P of the Lyapunov Equation is SD: (2) Solution of the Algebraic Riccati Equation is SD: (3) Solutions to finite horizon constrained quadratic optimization problems are SD. A. Jadbabaie “ESE 680: Distributed Dynamical systems”