CMPUT 680 Topic 2 Parsing and Lexical Analysis

CMPUT 680 Topic 2: Parsing and Lexical Analysis José Nelson Amaral 1

Reading List Appel, Chapter 2, 3, 4, and 5 Aho. Sethi. Ullman, Chapter 2, 3, 4, and 5 2

Some Important Basic Definitions lexical: of or relating to the morphemes of a language. morpheme: a meaningul linguistic unit that cannot be divided into smaller meaningful parts. lexical analysis: the task concerned with breaking an input into its smallest meaningful units, called tokens. 3

Some Important Basic Definitions syntax: the way in which words are put together to form phrases, clauses, or sentences. The rules governing the formation of statements in a programming language. syntax analysis: the task concerned with fitting a sequence of tokens into a specified syntax. parsing: To break a sentence down into its component parts of speech with an explanation of the form, function, and syntactical relationship of each part. 4

Some Important Basic Definitions parsing = lexical analysis + syntax analysis semantic analysis: the task concerned with calculating the program’s meaning. 5

Regular Expressions Symbol: a A regular expression formed by a. Alternation: M | N A regular expression formed by M or N. Concatenation: M • N A regular expression formed by M followed by N. Epsilon: ε Repetition: M* The empty string. A regular expression formed by zero or more repetitions of M. 6

Building a Recognizer for a Language General approach: 1. Build a deterministic finite automaton (DFA) from regular expression E 2. Execute the DFA to determine whether an input string belongs to L(E) Note: The DFA construction is done automatically by a tool such as lex. 7

Finite Automata A nondeterministic finite automaton A = {S, Σ, s 0, F, move } consists of: 1. A set of states S 2. A set of input symbols Σ (the input symbol alphabet) 3. A state s 0 that is distinguished as the start state 4. A state F distinguished as the accepting state 5. A transition function move that maps state-symbol pairs into sets of state. In a Deterministic Finite State Automata (DFA), the function move maps each state-symbol pair into a unique state. 8

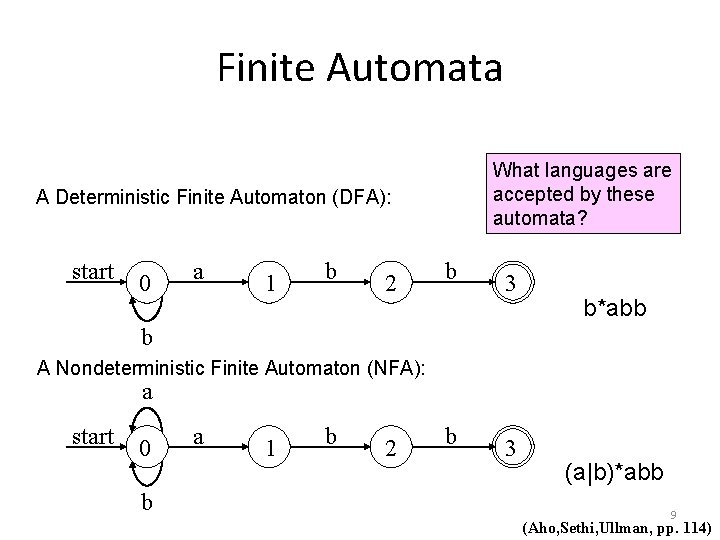
Finite Automata What languages are accepted by these automata? A Deterministic Finite Automaton (DFA): start 0 a 1 b 2 b 3 b*abb b A Nondeterministic Finite Automaton (NFA): a start 0 b a 1 b 2 b 3 (a|b)*abb 9 (Aho, Sethi, Ullman, pp. 114)

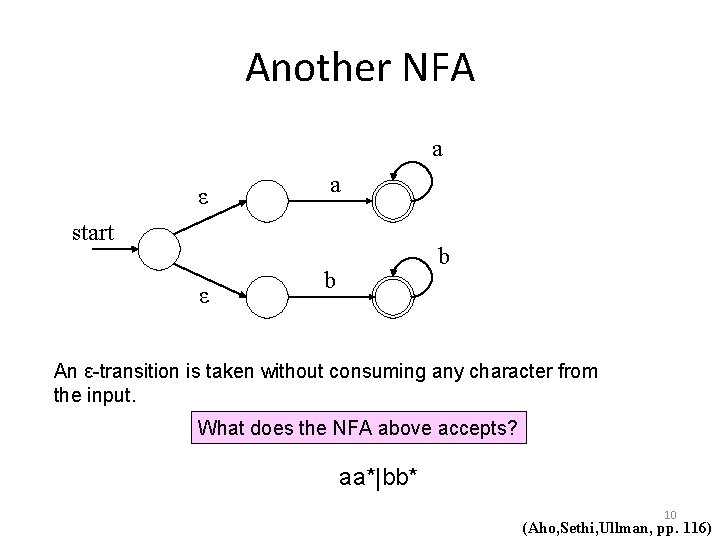
Another NFA a ε a start ε b b An ε-transition is taken without consuming any character from the input. What does the NFA above accepts? aa*|bb* 10 (Aho, Sethi, Ullman, pp. 116)

Constructing NFA How do we define an NFA that accepts a regular expression? It is very simple. Remember that a regular expression is formed by the use of alternation, concatenation, and repetition. Thus all we need to do is to know how to build the NFA for a single symbol, and how to compose NFAs. 11

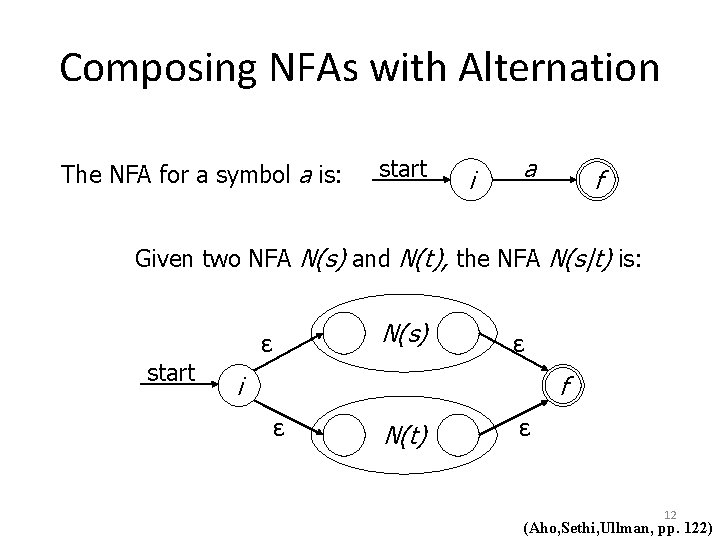
Composing NFAs with Alternation The NFA for a symbol a is: start i a f Given two NFA N(s) and N(t), the NFA N(s|t) is: N(s) ε start ε i f ε N(t) ε 12 (Aho, Sethi, Ullman, pp. 122)

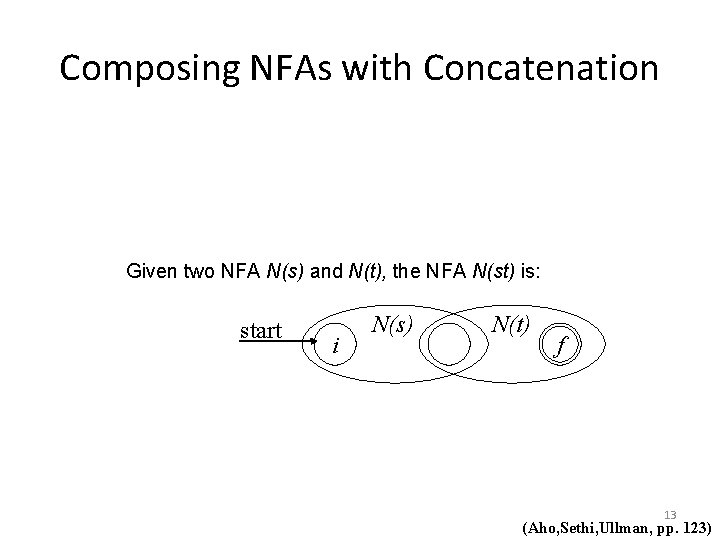
Composing NFAs with Concatenation Given two NFA N(s) and N(t), the NFA N(st) is: start i N(s) N(t) f 13 (Aho, Sethi, Ullman, pp. 123)

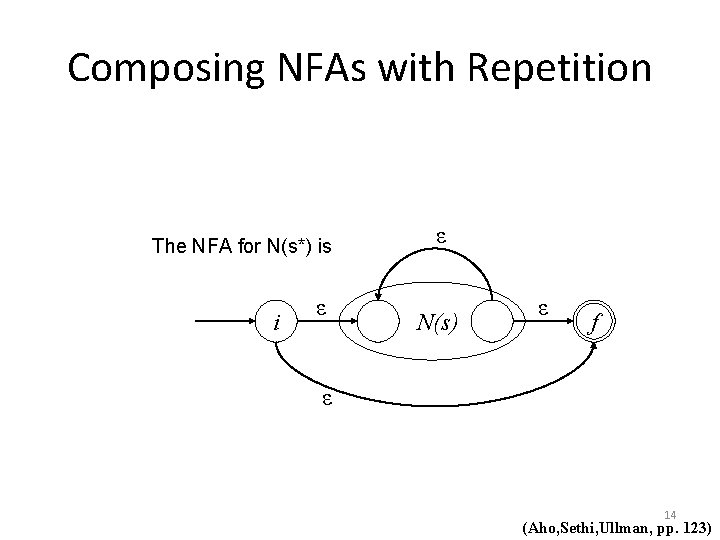
Composing NFAs with Repetition The NFA for N(s*) is i ε ε N(s) ε f ε 14 (Aho, Sethi, Ullman, pp. 123)

NFA Properties • Following these construction rules, we obtain an NFA N(r) with these properties: – N(r) has at most twice as many states as the number of symbols and operators in r; – N(r) has exactly one starting and one accepting state; – Each state of N(r) has at most one outgoing transition on a symbol of the alphabet Σ or at most two outgoing ε-transitions. 15 (Aho, Sethi, Ullman, pp. 124)

How to Parse a Regular Expression? Given a DFA, we can generate an automaton that recognizes the longest substring of an input that is a valid token. Using the three simple rules presented, it is easy to generate an NFA to recognize a regular expression. Given a regular expression, how do we generate an automaton to recognize tokens? Create an NFA and convert it to a DFA. 16

Regular expression notation: An Example a ε An ordinary character stands for itself. The empty string. Another way to write the empty string. M|N Alternation, Choosing from M or N. MN Concatenation, an M followed by an N. M* Repetition (zero or more times). M+ Repetition (one or more times). M? Optional, zero or one occurrence of M. [a -z. A -Z] Character set alternation. . Stands for any single character except newline. “a. +*” Quotation, a string in quotes stands for itself literally. 17 (Appel, pp. 20)

Regular expressions for some tokens if {return IF; } [a - z] [a - z 0 - 9 ] * {return ID; } [0 - 9] + {return NUM; } ([0 - 9] + “. ” [0 - 9] *) | ([0 - 9] * “. ” [0 - 9] +) {return REAL; } (“--” [a - z]* “n”) | (“ ” | “ n ” | “ t ”) + {/* do nothing*/} . {error (); } 18 (Appel, pp. 20)

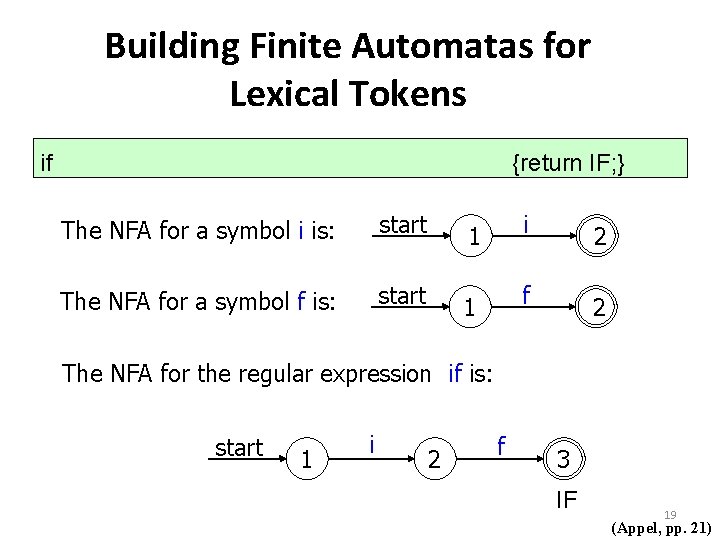
Building Finite Automatas for Lexical Tokens if {return IF; } The NFA for a symbol i is: start 1 i 2 The NFA for a symbol f is: start 1 f 2 The NFA for the regular expression if is: start 1 i 2 f 3 IF 19 (Appel, pp. 21)

Building Finite Automatas for Lexical Tokens [a-z] [a-z 0 -9 ] * {return ID; } a-z start 1 a-z 2 ID 0 -9 20 (Appel, pp. 21)

Building Finite Automatas for Lexical Tokens [0 - 9] + {return NUM; } start 1 0 -9 2 NUM 0 -9 21 (Appel, pp. 21)

Building Finite Automatas for Lexical Tokens ([0 - 9] + “. ” [0 - 9] *) | ([0 - 9] * “. ” [0 - 9] +) {return REAL; } 0 -9 start 1 0 -9. 4 2 0 -9. 5 3 0 -9 REAL 22 (Appel, pp. 21)

Building Finite Automatas for Lexical Tokens ([0 - 9] + “. ” [0 - 9] *) | ([0 - 9] * “. ” [0 - 9] +) {return REAL; } 0 -9 start 1 ε 6 0 -9. 4 2 0 -9. 5 3 0 -9 REAL 23 (Appel, pp. 21)

Building Finite Automatas for Lexical Tokens (“--” [a - z]* “n”) | (“ ” | “ n ” | “ t ”) + {/* do nothing*/} a-z start 1 blank t 2 n n 5 blank 3 n 4 /* do nothing */ t 24 (Appel, pp. 21)

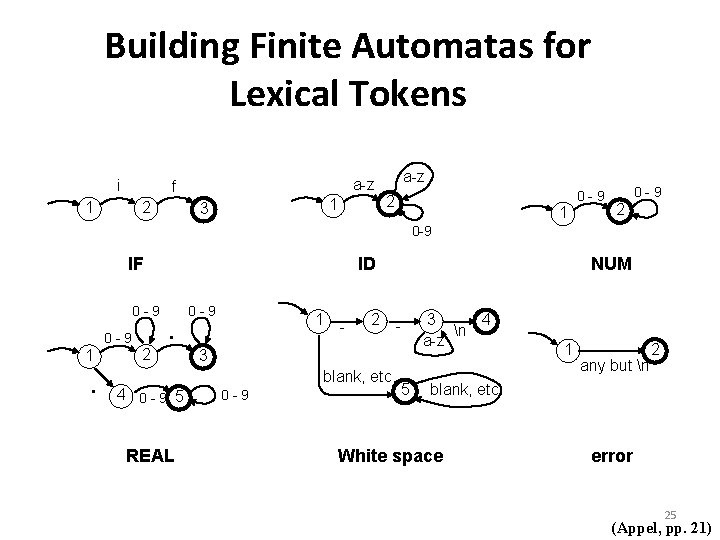
Building Finite Automatas for Lexical Tokens i a-z f 2 1 1 3 a-z 2 1 0 -9 2 0 -9 IF 0 -9 1 . ID . 2 0 -9 1 - 2 - 3 blank, etc. 4 0 -9 5 REAL NUM 0 -9 5 3 4 n a-z 1 any but n 2 blank, etc. White space error 25 (Appel, pp. 21)

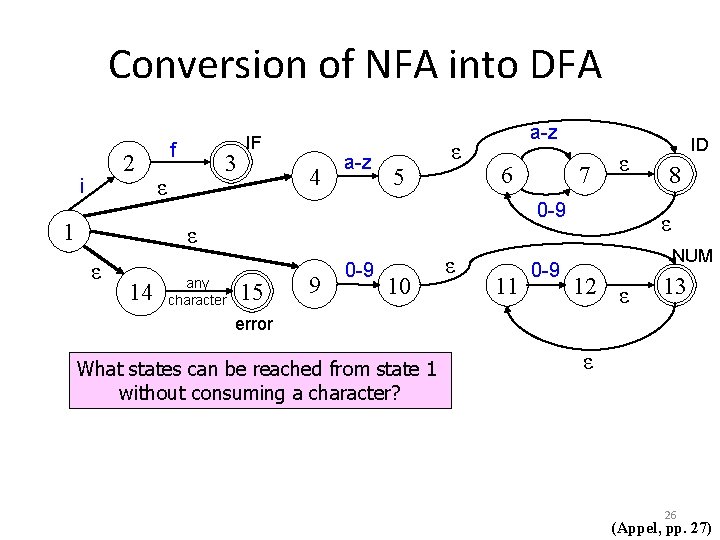
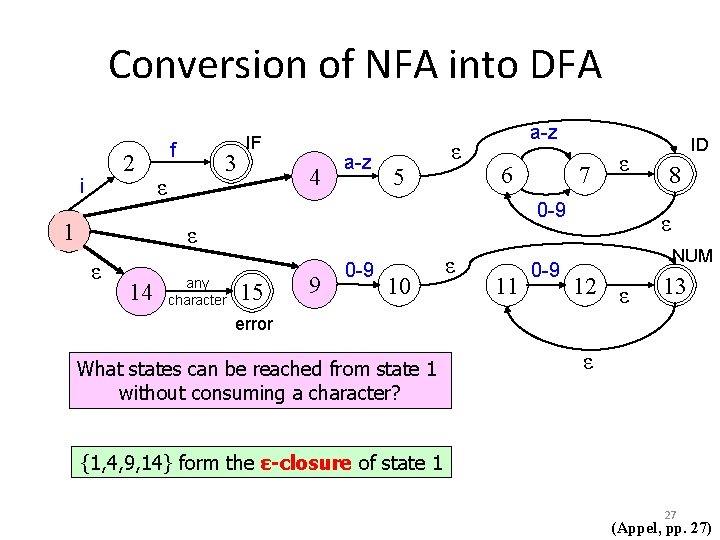
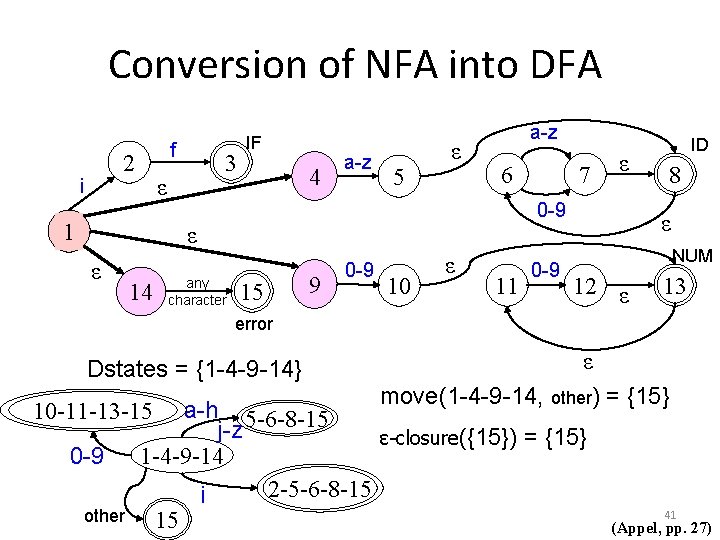
Conversion of NFA into DFA 2 i 1 f 3 ε IF 4 a-z 5 ε a-z 6 14 any character ε 0 -9 ε ε 7 15 9 0 -9 10 ε 11 0 -9 ID 8 ε NUM 12 ε 13 error What states can be reached from state 1 without consuming a character? ε 26 (Appel, pp. 27)

Conversion of NFA into DFA 2 i 1 f 3 ε IF 4 a-z 5 ε a-z 6 14 any character ε 0 -9 ε ε 7 15 9 0 -9 10 ε 11 0 -9 ID 8 ε NUM 12 ε 13 error What states can be reached from state 1 without consuming a character? ε {1, 4, 9, 14} form the ε-closure of state 1 27 (Appel, pp. 27)

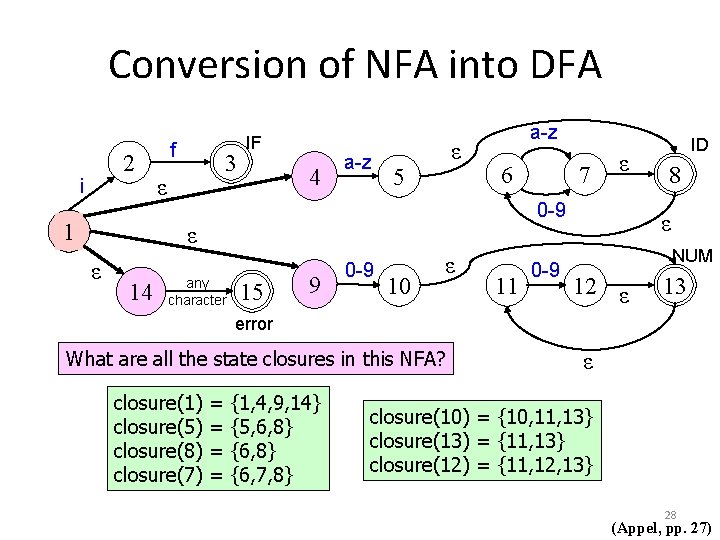
Conversion of NFA into DFA 2 i 1 f 3 ε IF 4 a-z ε 5 a-z 6 14 ε 0 -9 ε ε 7 any character 15 9 0 -9 10 ε 11 0 -9 ID 8 ε NUM 12 ε 13 error What are all the state closures in this NFA? closure(1) closure(5) closure(8) closure(7) = = {1, 4, 9, 14} {5, 6, 8} {6, 7, 8} ε closure(10) = {10, 11, 13} closure(13) = {11, 13} closure(12) = {11, 12, 13} 28 (Appel, pp. 27)

Conversion of NFA into DFA Given a set of NFA states T, the ε-closure(T) is the set of states that are reachable through ε-transiton from any state s ∈T. Given a set of NFA states T, move(T, a) is the set of states that are reachable on input a from any state s∈T. 29 (Aho, Sethi, Ullman, pp. 118)

Problem Statement for Conversion of NFA into DFA Given an NFA find the DFA with the minimum number of states that has the same behavior as the NFA for all inputs. If the initial state in the NFA is s 0, then the set of states in the DFA, Dstates, is initialized with a state representing ε-closure(s 0). 30 (Aho, Sethi, Ullman, pp. 118)

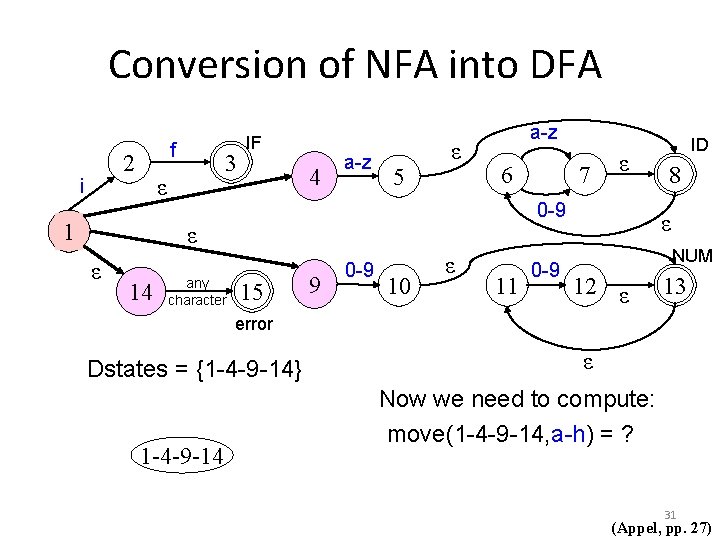
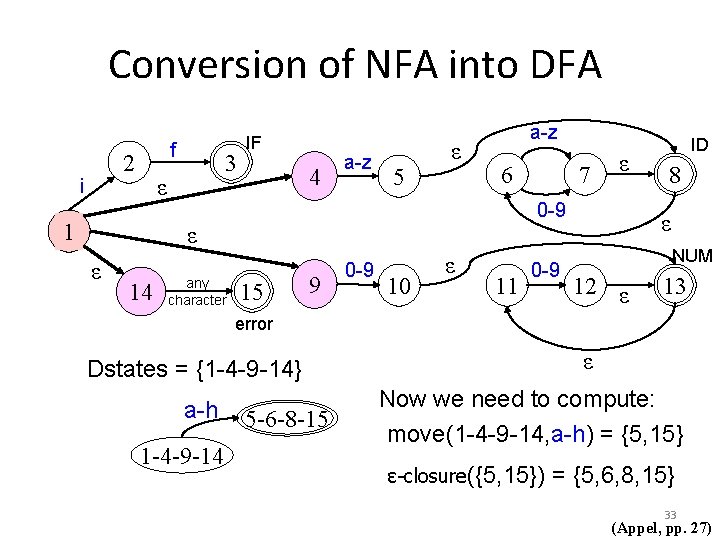
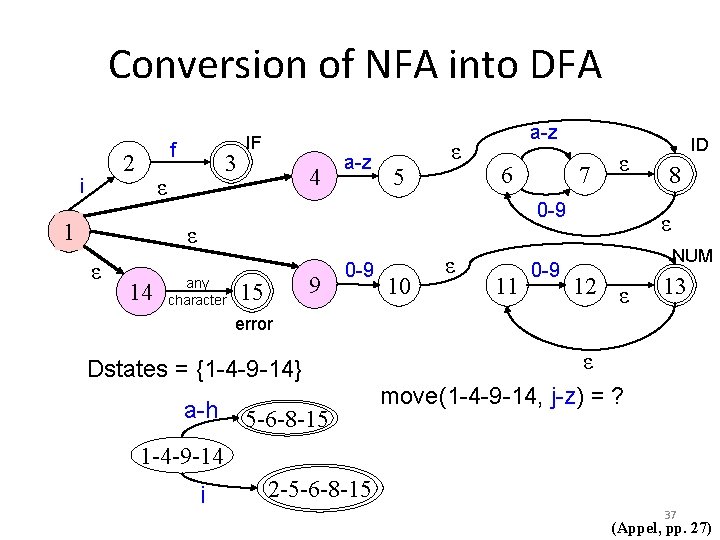
Conversion of NFA into DFA f 2 i 3 ε 1 IF 4 a-z 5 ε a-z 6 14 any character ε 0 -9 ε ε 7 15 9 0 -9 10 ε 11 0 -9 ID 8 ε NUM 12 ε 13 error Dstates = {1 -4 -9 -14} 1 -4 -9 -14 ε Now we need to compute: move(1 -4 -9 -14, a-h) = ? 31 (Appel, pp. 27)

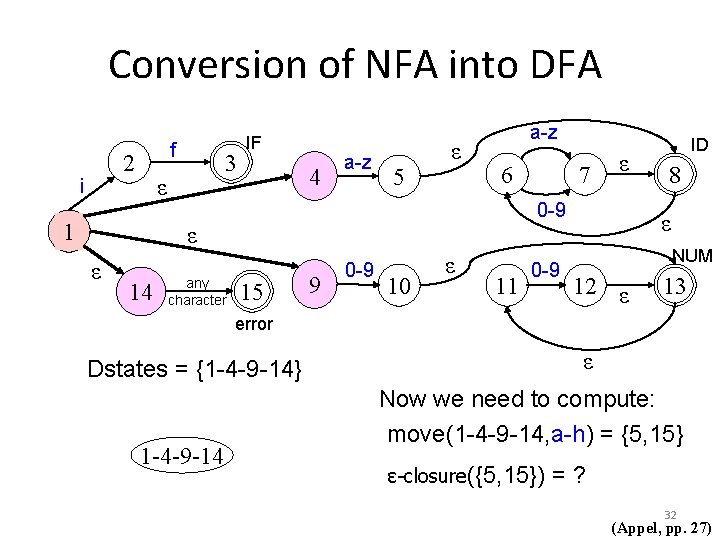
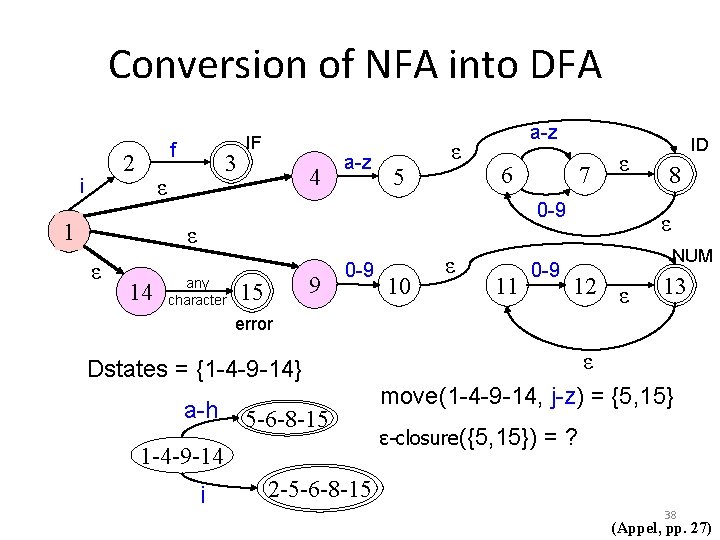
Conversion of NFA into DFA f 2 i 3 ε 1 IF 4 a-z 5 ε a-z 6 14 any character ε 0 -9 ε ε 7 15 9 0 -9 10 ε 11 0 -9 ID 8 ε NUM 12 ε 13 error ε Dstates = {1 -4 -9 -14} 1 -4 -9 -14 Now we need to compute: move(1 -4 -9 -14, a-h) = {5, 15} ε-closure({5, 15}) =? 32 (Appel, pp. 27)

Conversion of NFA into DFA f 2 i 3 ε 1 IF 4 a-z 5 ε a-z 6 14 any character ε 0 -9 ε ε 7 15 9 0 -9 10 ε 11 0 -9 ID 8 ε NUM 12 ε 13 error ε Dstates = {1 -4 -9 -14} a-h 1 -4 -9 -14 5 -6 -8 -15 Now we need to compute: move(1 -4 -9 -14, a-h) = {5, 15} ε-closure({5, 15}) = {5, 6, 8, 15} 33 (Appel, pp. 27)

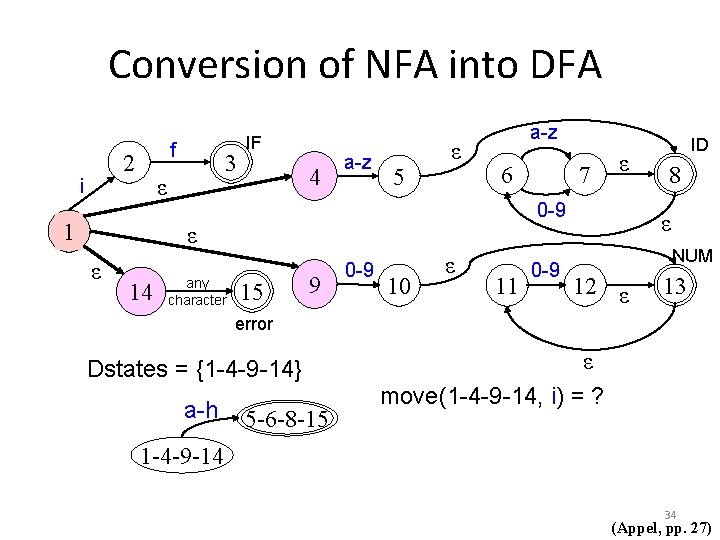
Conversion of NFA into DFA f 2 i 3 ε 1 IF 4 a-z 5 ε a-z 6 14 any character ε 0 -9 ε ε 7 15 9 0 -9 10 ε 11 0 -9 ID 8 ε NUM 12 ε 13 error Dstates = {1 -4 -9 -14} a-h 5 -6 -8 -15 ε move(1 -4 -9 -14, i) = ? 1 -4 -9 -14 34 (Appel, pp. 27)

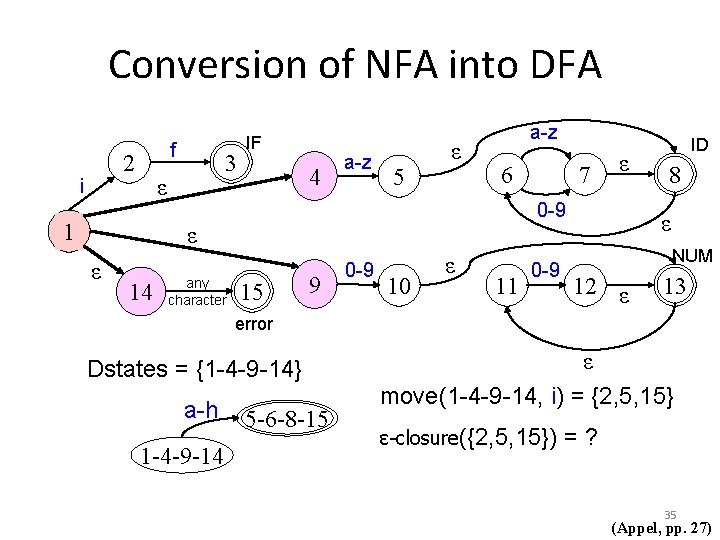
Conversion of NFA into DFA f 2 i 3 ε 1 IF 4 a-z 5 ε a-z 6 14 any character ε 0 -9 ε ε 7 15 9 0 -9 10 ε 11 0 -9 ID 8 ε NUM 12 ε 13 error Dstates = {1 -4 -9 -14} a-h 1 -4 -9 -14 5 -6 -8 -15 ε move(1 -4 -9 -14, i) = {2, 5, 15} ε-closure({2, 5, 15}) =? 35 (Appel, pp. 27)

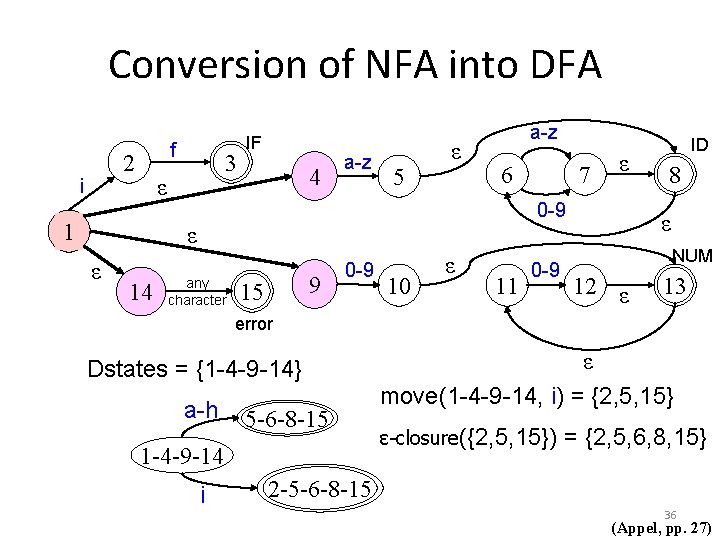
Conversion of NFA into DFA f 2 i 3 ε 1 IF 4 a-z 5 ε a-z 6 14 ε 0 -9 ε ε 7 any character 9 15 0 -9 10 ε 11 0 -9 ID 8 ε NUM 12 ε 13 error Dstates = {1 -4 -9 -14} a-h 5 -6 -8 -15 1 -4 -9 -14 i ε move(1 -4 -9 -14, i) = {2, 5, 15} ε-closure({2, 5, 15}) = {2, 5, 6, 8, 15} 2 -5 -6 -8 -15 36 (Appel, pp. 27)

Conversion of NFA into DFA f 2 i 3 ε 1 IF 4 a-z 5 ε a-z 6 14 ε 0 -9 ε ε 7 any character 9 15 0 -9 10 ε 11 0 -9 ID 8 ε NUM 12 ε 13 error Dstates = {1 -4 -9 -14} a-h 5 -6 -8 -15 ε move(1 -4 -9 -14, j-z) = ? 1 -4 -9 -14 i 2 -5 -6 -8 -15 37 (Appel, pp. 27)

Conversion of NFA into DFA f 2 i 3 ε 1 IF 4 a-z 5 ε a-z 6 14 ε 0 -9 ε ε 7 any character 9 15 0 -9 10 ε 11 0 -9 ID 8 ε NUM 12 ε 13 error Dstates = {1 -4 -9 -14} a-h 5 -6 -8 -15 1 -4 -9 -14 i ε move(1 -4 -9 -14, j-z) = {5, 15} ε-closure({5, 15}) =? 2 -5 -6 -8 -15 38 (Appel, pp. 27)

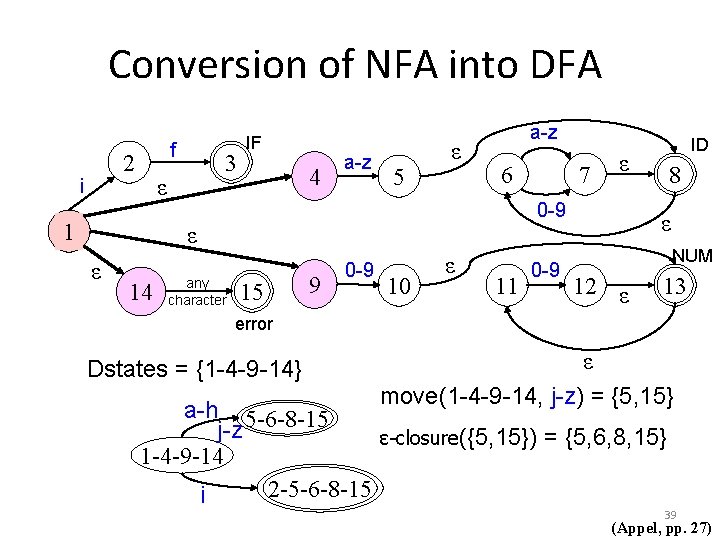
Conversion of NFA into DFA f 2 i 3 ε 1 IF 4 a-z 5 ε a-z 6 14 any character ε 0 -9 ε ε 7 15 9 0 -9 10 ε 11 0 -9 ID 8 ε NUM 12 ε 13 error Dstates = {1 -4 -9 -14} ε move(1 -4 -9 -14, j-z) = {5, 15} a-h 5 -6 -8 -15 j-z ε-closure({5, 15}) = {5, 6, 8, 15} 1 -4 -9 -14 2 -5 -6 -8 -15 i 39 (Appel, pp. 27)

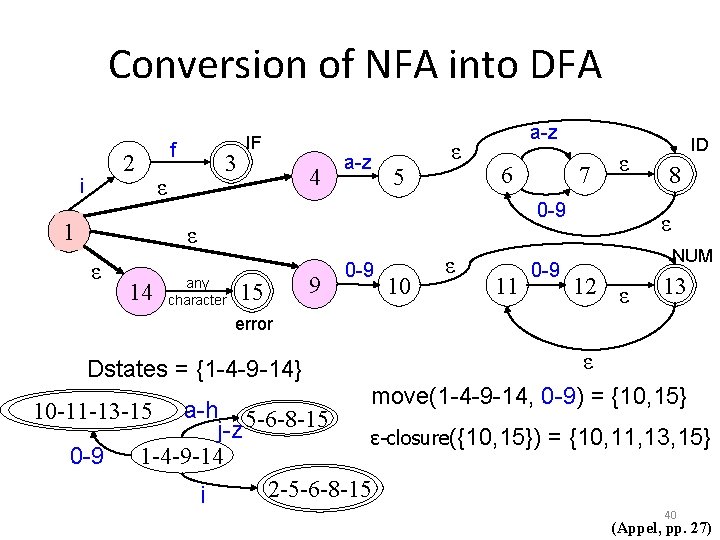
Conversion of NFA into DFA f 2 i 3 ε 1 IF 4 a-z 5 ε a-z 6 14 any character ε 0 -9 ε ε 7 15 9 0 -9 10 ε 11 0 -9 ID 8 ε NUM 12 ε 13 error Dstates = {1 -4 -9 -14} a-h 5 -6 -8 -15 j-z ε-closure({10, 15}) = {10, 11, 13, 15} 1 -4 -9 -14 2 -5 -6 -8 -15 i 10 -11 -13 -15 0 -9 ε move(1 -4 -9 -14, 0 -9) = {10, 15} 40 (Appel, pp. 27)

Conversion of NFA into DFA f 2 i 3 ε 1 IF 4 a-z 5 ε a-z 6 14 any character ε 0 -9 ε ε 7 15 9 0 -9 10 ε 11 0 -9 ID 8 ε NUM 12 ε 13 error Dstates = {1 -4 -9 -14} a-h 5 -6 -8 -15 j-z ε-closure({15}) = {15} 1 -4 -9 -14 2 -5 -6 -8 -15 i 15 10 -11 -13 -15 0 -9 other ε move(1 -4 -9 -14, other) = {15} 41 (Appel, pp. 27)

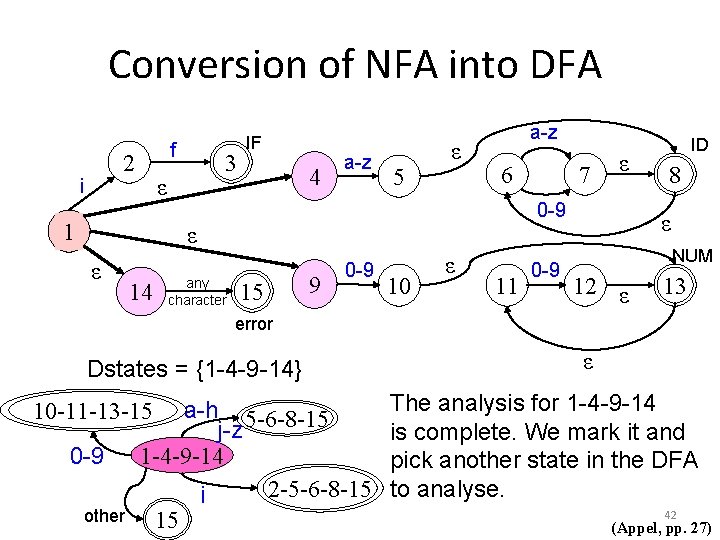
Conversion of NFA into DFA f 2 i 3 ε 1 IF 4 a-z 5 ε a-z 6 14 any character ε 0 -9 ε ε 7 15 9 0 -9 10 ε 11 0 -9 ID 8 ε NUM 12 ε 13 error Dstates = {1 -4 -9 -14} a-h 5 -6 -8 -15 j-z 1 -4 -9 -14 2 -5 -6 -8 -15 i 15 10 -11 -13 -15 0 -9 other ε The analysis for 1 -4 -9 -14 is complete. We mark it and pick another state in the DFA to analyse. 42 (Appel, pp. 27)

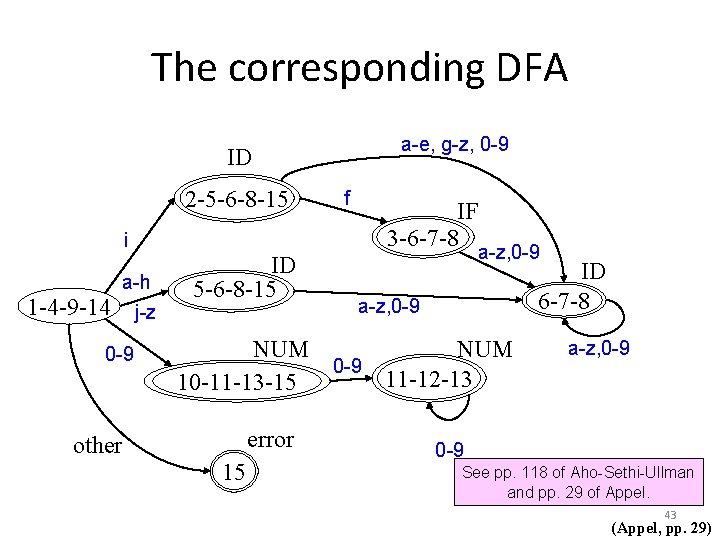
The corresponding DFA a-e, g-z, 0 -9 ID 2 -5 -6 -8 -15 i 1 -4 -9 -14 a-h j-z 0 -9 ID 5 -6 -8 -15 f IF 3 -6 -7 -8 a-z, 0 -9 ID 6 -7 -8 a-z, 0 -9 NUM 0 -9 11 -12 -13 10 -11 -13 -15 error other 15 a-z, 0 -9 See pp. 118 of Aho-Sethi-Ullman and pp. 29 of Appel. 43 (Appel, pp. 29)

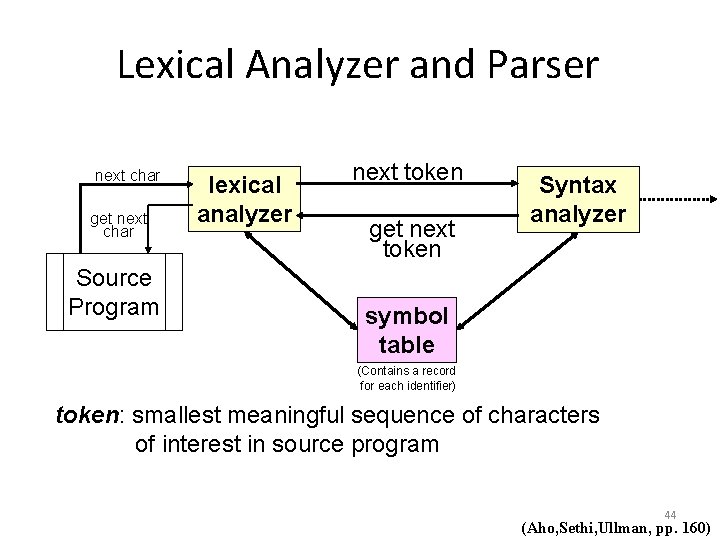
Lexical Analyzer and Parser next char get next char Source Program lexical analyzer next token get next token Syntax analyzer symbol table (Contains a record for each identifier) token: smallest meaningful sequence of characters of interest in source program 44 (Aho, Sethi, Ullman, pp. 160)

Definition of Context-Free Grammars A context-free grammar G = (T, N, S, P) consists of: 1. T, a set of terminals (scanner tokens). 2. N, a set of nonterminals (syntactic variables generated by productions). 3. S, a designated start nonterminal. 4. P, a set of productions. Each production has the form, A: : = α , where A is a nonterminal and α is a sentential form , i. e. , a string of zero or more grammar symbols (terminals/nonterminals). 45

Syntax Analysis Problem Statement: To find a derivation sequence in a grammar G for the input token stream (or say that none exists). 46

Parse trees A parse tree is a graphical representation of a derivation sequence of a sentential form. Tree nodes represent symbols of the grammar (nonterminals or terminals) and tree edges represent derivation steps. 47

Derivation Given the following grammar: E → E + E | E ∗ E | ( E ) | - E | id Is the string -(id + id) a sentence in this grammar? Yes because there is the following derivation: E ⇒ -(E) ⇒ -(E + E) ⇒ -(id + id) Where ⇒ reads “derives in one step”. 48 (Aho, Sethi, Ullman, pp. 168)

Notation: ⇒ reads “derives in one step. ” ∗ ⇒ reads “derives in zero or more steps. ” + ⇒ reads “derives in one or more steps. ” 49 (Aho, Sethi, Ullman, pp. 168)

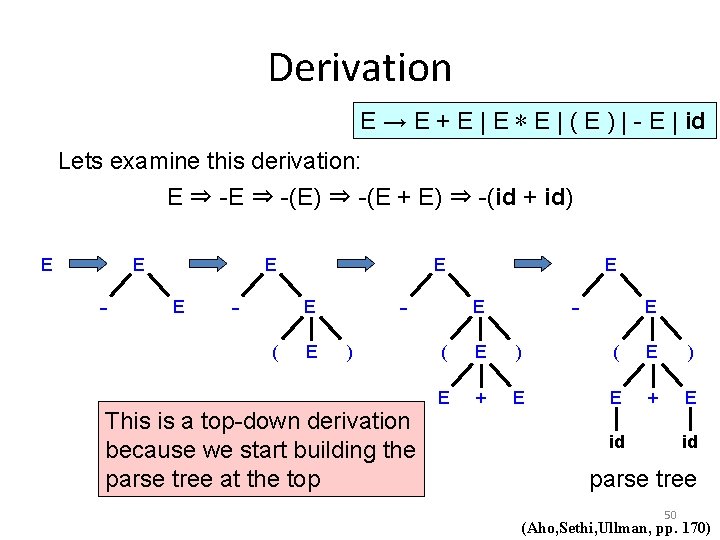
Derivation E → E + E | E ∗ E | ( E ) | - E | id Lets examine this derivation: E ⇒ -(E) ⇒ -(E + E) ⇒ -(id + id) E E - E - E ( E ) This is a top-down derivation because we start building the parse tree at the top E - E E ( E ) E + E id id parse tree 50 (Aho, Sethi, Ullman, pp. 170)

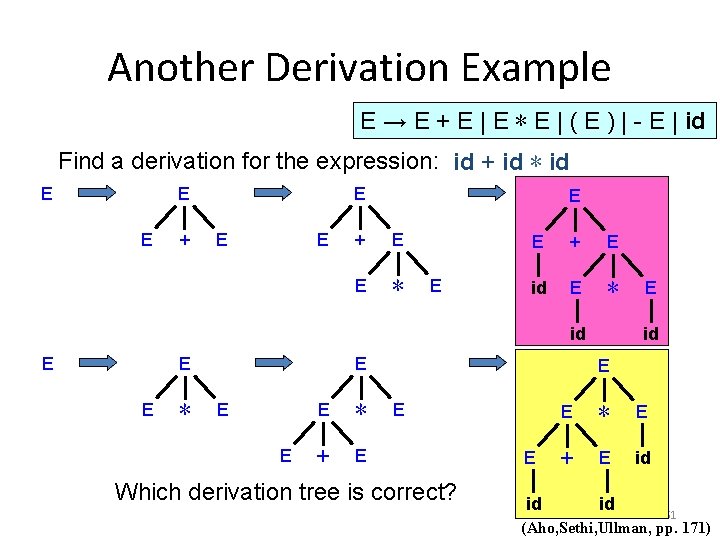
Another Derivation Example E → E + E | E ∗ E | ( E ) | - E | id Find a derivation for the expression: id + id ∗ id E E E + E E ∗ E E + E id E ∗ id E E + E Which derivation tree is correct? E E E id E ∗ E + E id id 51 (Aho, Sethi, Ullman, pp. 171)

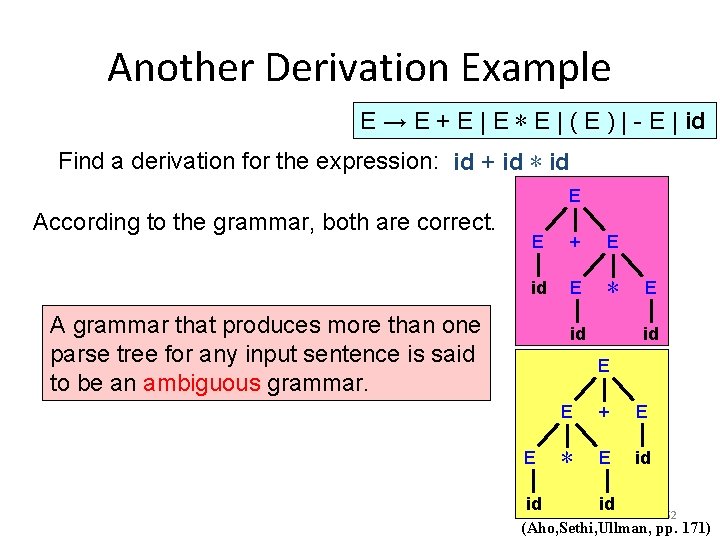
Another Derivation Example E → E + E | E ∗ E | ( E ) | - E | id Find a derivation for the expression: id + id ∗ id E According to the grammar, both are correct. E + E id E ∗ A grammar that produces more than one parse tree for any input sentence is said to be an ambiguous grammar. id E E id E + E ∗ E id id 52 (Aho, Sethi, Ullman, pp. 171)

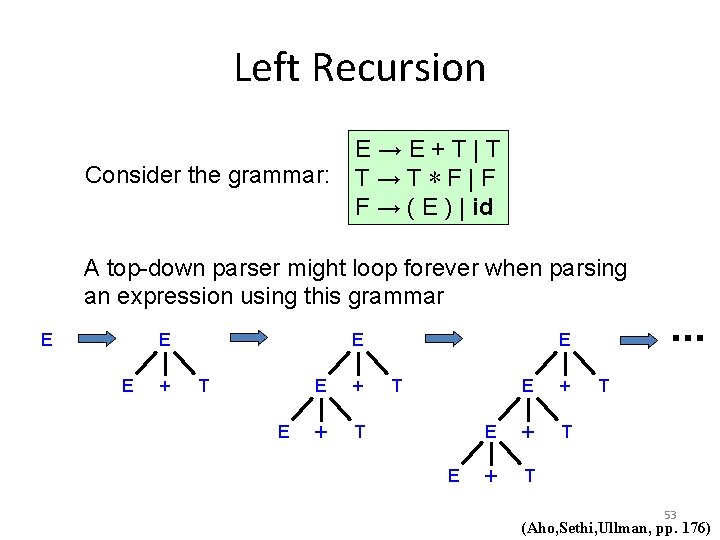
Left Recursion Consider the grammar: E→E+T|T T→T∗F|F F → ( E ) | id A top-down parser might loop forever when parsing an expression using this grammar E E E + E T E E + + T E E + T + T T 53 (Aho, Sethi, Ullman, pp. 176)

Left Recursion Consider the grammar: E→E+T|T T→T∗F|F F → ( E ) | id A grammar that has at least one production of the form A ⇒Aα is a left recursive grammar. Top-down parsers do not work with left-recursive grammars. Left-recursion can often be eliminated by rewriting the grammar. 54 (Aho, Sethi, Ullman, pp. 176)

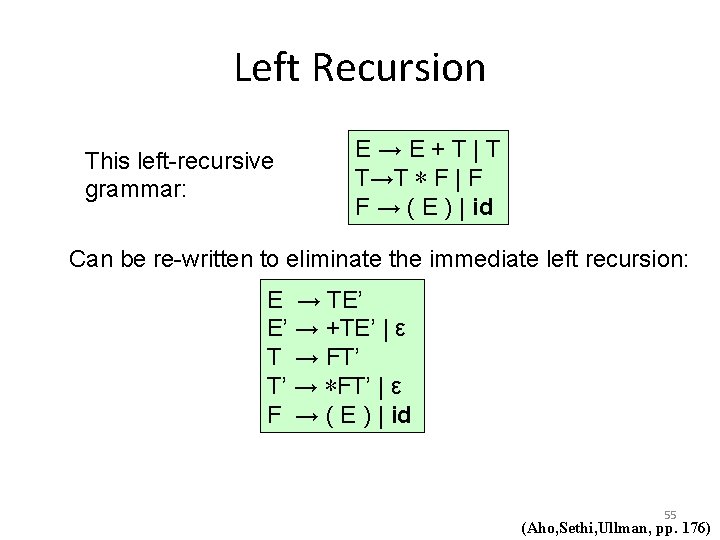
Left Recursion This left-recursive grammar: E→E+T|T T→T ∗ F | F F → ( E ) | id Can be re-written to eliminate the immediate left recursion: E → TE’ E’ → +TE’ | ε T → FT’ T’ → ∗FT’ | ε F → ( E ) | id 55 (Aho, Sethi, Ullman, pp. 176)

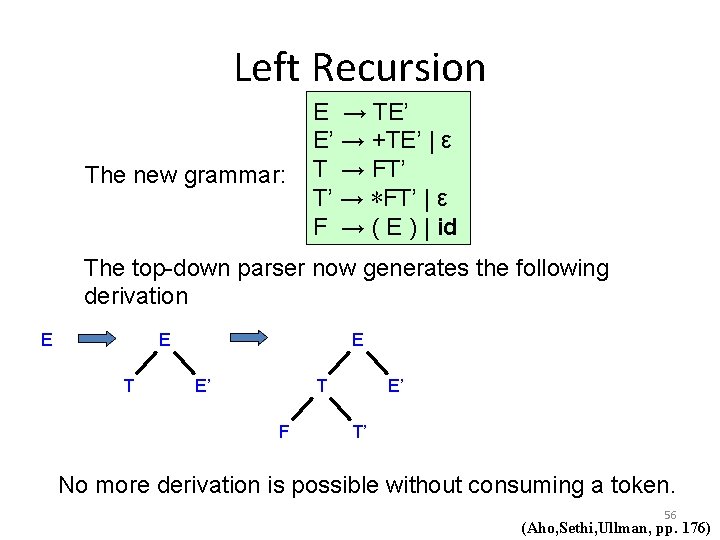
Left Recursion The new grammar: E → TE’ E’ → +TE’ | ε T → FT’ T’ → ∗FT’ | ε F → ( E ) | id The top-down parser now generates the following derivation E E T E E’ T F E’ T’ No more derivation is possible without consuming a token. 56 (Aho, Sethi, Ullman, pp. 176)

Eliminating Left Recursion A left-recursive production of the form: A→Aα|β Can always be rewritten as two productions: A→βR R→αR|ε Example: expr → expr + term | term After rewriting: expr → term R R → + term | ε 57

But, is this right? 58

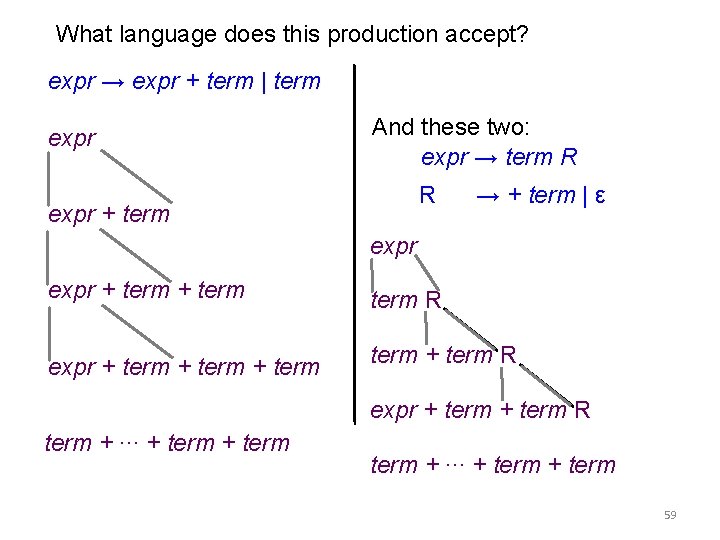
What language does this production accept? expr → expr + term | term expr And these two: expr → term R R expr + term → + term | ε expr + term R expr + term + term R expr + term R term + ∙∙∙ + term 59

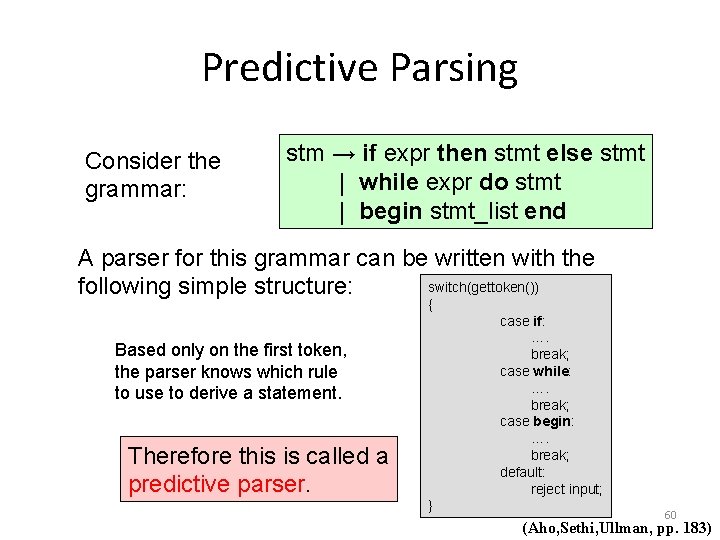
Predictive Parsing Consider the grammar: stm → if expr then stmt else stmt | while expr do stmt | begin stmt_list end A parser for this grammar can be written with the switch(gettoken()) following simple structure: { case if: …. break; case while: …. break; case begin: …. break; default: reject input; Based only on the first token, the parser knows which rule to use to derive a statement. Therefore this is called a predictive parser. } 60 (Aho, Sethi, Ullman, pp. 183)

Left Factoring The following grammar: stmt → if expr then stmt else stmt | if expr then stmt Cannot be parsed by a predictive parser that looks one element ahead. But the grammar can be re-written: stmt → if expr then stmt’ stmt‘→ else stmt | ε Where ε is the empty string. Rewriting a grammar to eliminate multiple productions starting with the same token is called left factoring. 61 (Aho, Sethi, Ullman, pp. 178)

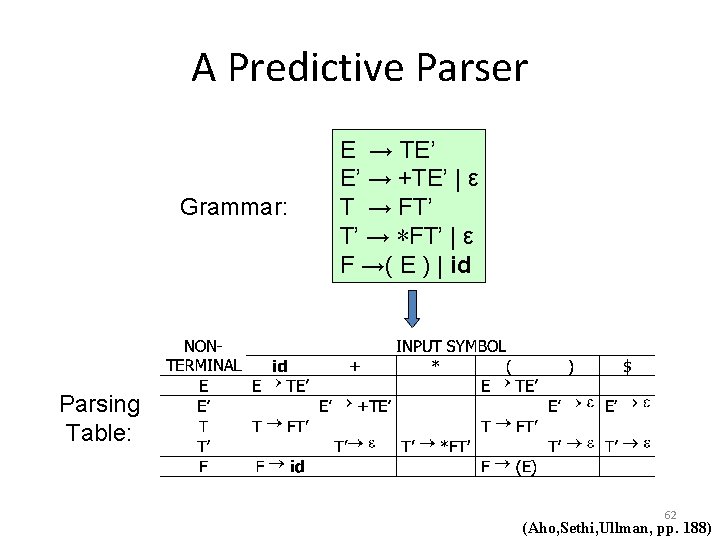
A Predictive Parser Grammar: E → TE’ E’ → +TE’ | ε T → FT’ T’ → ∗FT’ | ε F →( E ) | id Parsing Table: 62 (Aho, Sethi, Ullman, pp. 188)

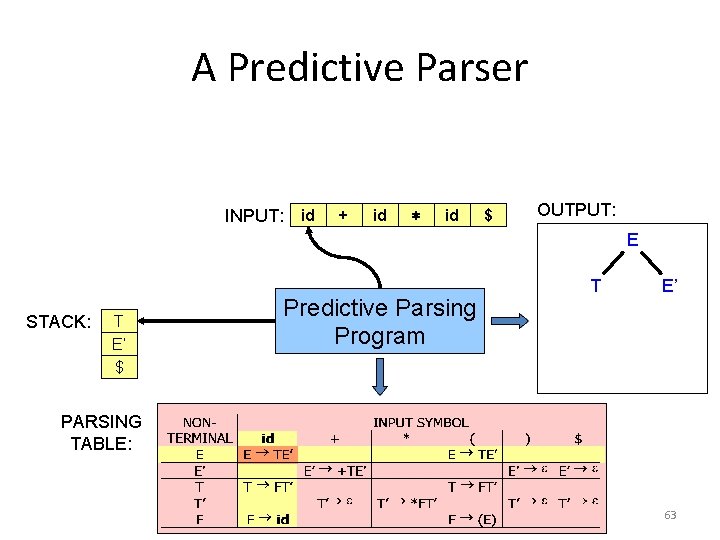
A Predictive Parser INPUT: id + id ∗ id $ OUTPUT: E STACK: E T E’ $ $ Predictive Parsing Program T E’ PARSING TABLE: 63

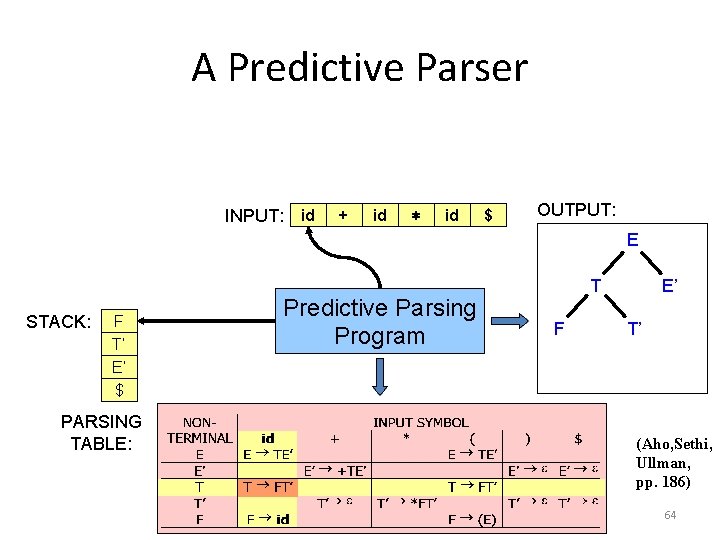
A Predictive Parser INPUT: id + id ∗ id $ OUTPUT: E STACK: F T E’ T’ E’ $ $ PARSING TABLE: Predictive Parsing Program T F E’ T’ (Aho, Sethi, Ullman, pp. 186) 64

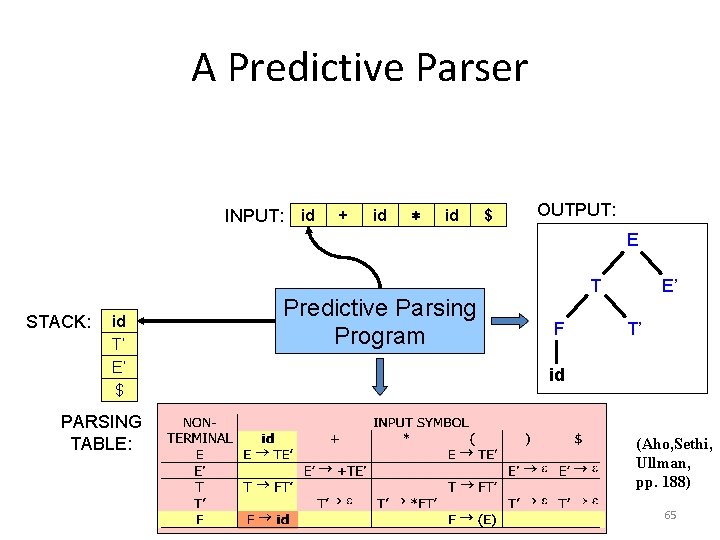
A Predictive Parser INPUT: id + id ∗ id $ OUTPUT: E STACK: id T F E’ T’ E’ $ $ PARSING TABLE: Predictive Parsing Program T F E’ T’ id (Aho, Sethi, Ullman, pp. 188) 65

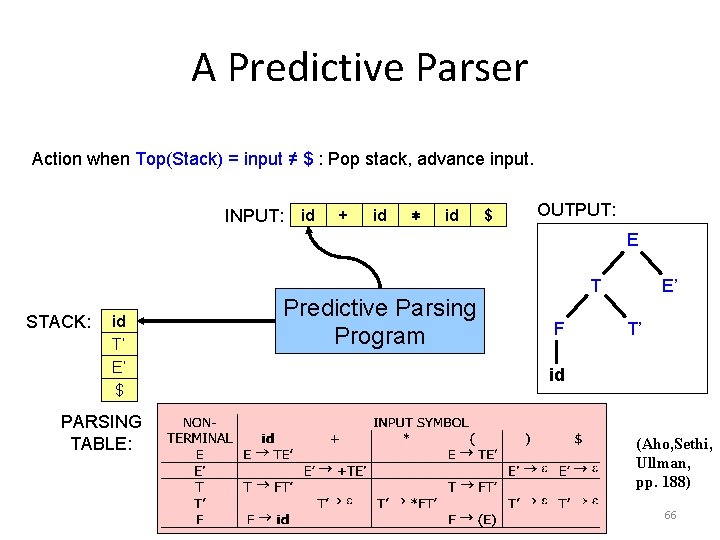
A Predictive Parser Action when Top(Stack) = input ≠ $ : Pop stack, advance input. INPUT: id + id ∗ id $ OUTPUT: E STACK: id F T’ E’ $ PARSING TABLE: Predictive Parsing Program T F E’ T’ id (Aho, Sethi, Ullman, pp. 188) 66

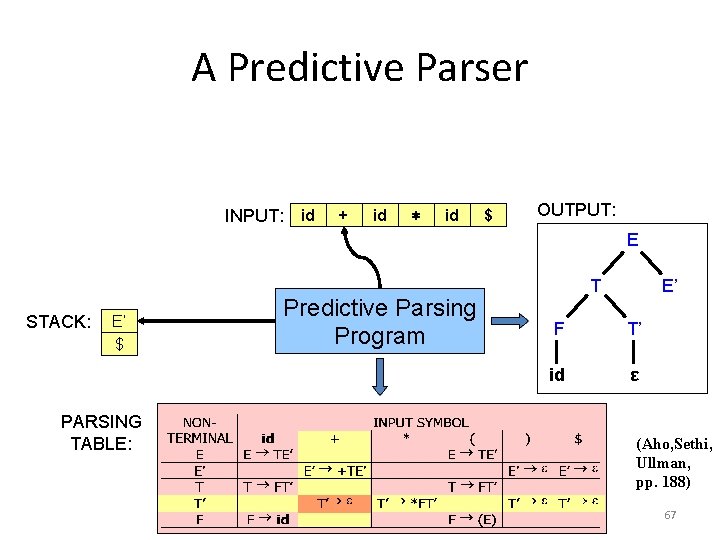
A Predictive Parser INPUT: id + id ∗ id $ OUTPUT: E STACK: E’ T’ E’ $ $ PARSING TABLE: Predictive Parsing Program T E’ F T’ id ε (Aho, Sethi, Ullman, pp. 188) 67

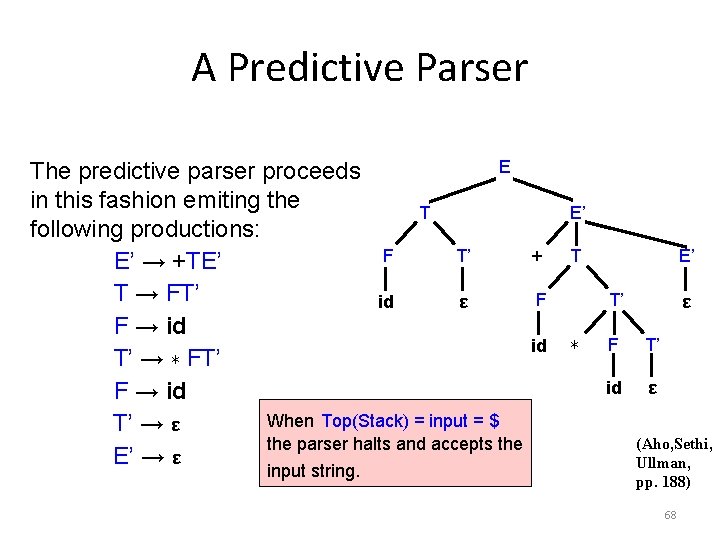
A Predictive Parser E The predictive parser proceeds in this fashion emiting the T following productions: F T’ E’ → +TE’ T → FT’ id ε F → id T’ → ∗ FT’ F → id When Top(Stack) = input = $ T’ → ε the parser halts and accepts the E’ → ε input string. E’ + T F id E’ T’ ∗ ε F T’ id ε (Aho, Sethi, Ullman, pp. 188) 68

LL(k) Parser This parser parses from left to right, and does a leftmost-derivation. It looks up 1 symbol ahead to choose its next action. Therefore, it is known as a LL(1) parser. An LL(k) parser looks k symbols ahead to decide its action. 69

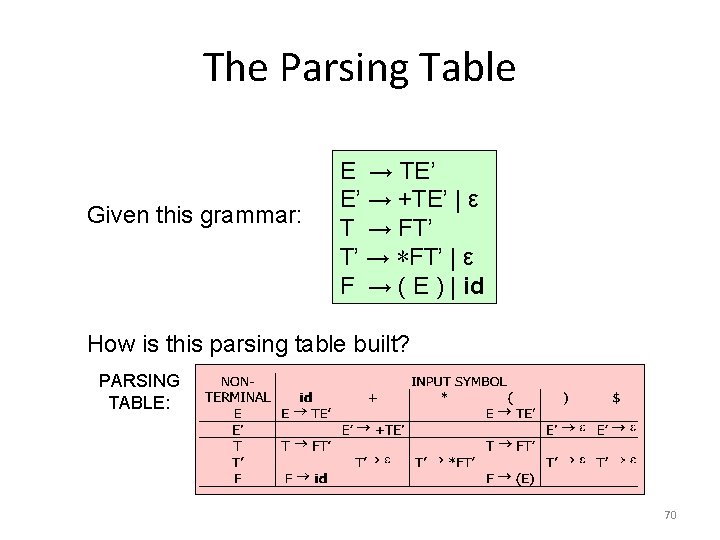
The Parsing Table Given this grammar: E → TE’ E’ → +TE’ | ε T → FT’ T’ → ∗FT’ | ε F → ( E ) | id How is this parsing table built? PARSING TABLE: 70

FIRST and FOLLOW We need to build a FIRST set and a FOLLOW set for each symbol in the grammar. The elements of FIRST and FOLLOW are terminal symbols. FIRST(α) is the set of terminal symbols that can begin any string derived from α. FOLLOW(α) is the set of terminal symbols that can follow α: t ∈ FOLLOW(α) ↔ ∃ derivation containing αt 71 (Aho, Sethi, Ullman, pp. 189)

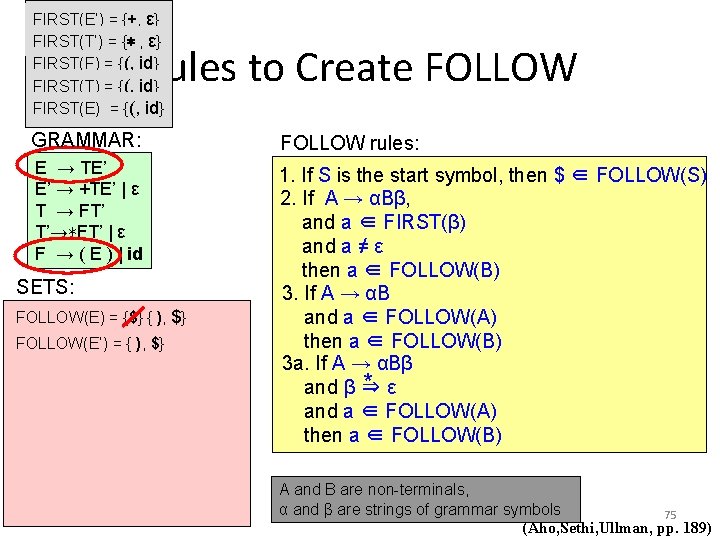
Rules to Create FIRST GRAMMAR: FIRST rules: E → TE’ E’ → +TE’ | ε T → FT’ T’→∗FT’ | ε F → ( E ) | id 1. If X is a terminal, FIRST(X) = {X} 2. If X → ε , then ε ∈ FIRST(X) 3. If X → Y 1 Y 2 • • • Yk * ε and Y 1 • • • Yi-1 ⇒ and a ∈FIRST(Yi) then a ∈ FIRST(X) SETS: FIRST(id) = {id} FIRST(∗) = {∗} FIRST(+) = {+} FIRST(() = {(} FIRST()) = {)} FIRST(E’) = {ε} FIRST(T’) = {ε} 72 (Aho, Sethi, Ullman, pp. 189)

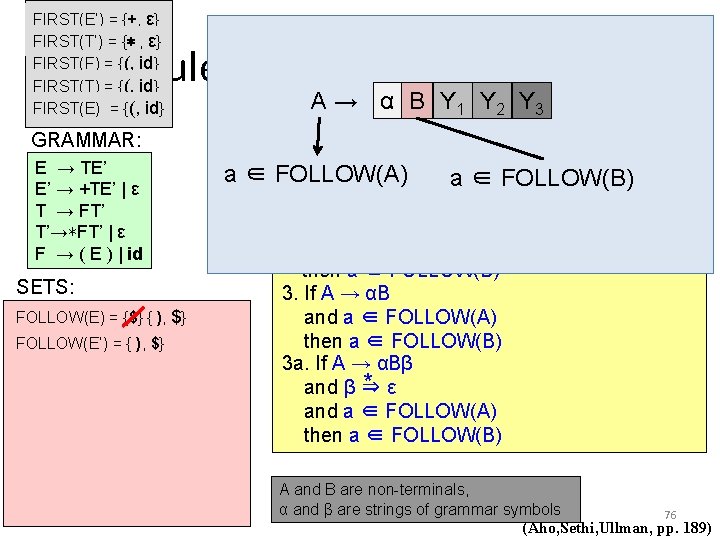
Rules to Create FIRST GRAMMAR: FIRST rules: E → TE’ E’ → +TE’ | ε T → FT’ T’→∗FT’ | ε F → ( E ) | id 1. If X is a terminal, FIRST(X) = {X} 2. If X → ε , then ε ∈ FIRST(X) 3. If X → Y 1 Y 2 • • • Yk * ε and Y 1 • • • Yi-1 ⇒ and a ∈FIRST(Yi) then a ∈ FIRST(X) SETS: X → Y 1 Y 2 Y 3 Y 4 Y 5 Y 6 a ∈ FIRST(X) a ∈ FIRST(Y 5) 73 (Aho, Sethi, Ullman, pp. 189)

Rules to Create FIRST GRAMMAR: E → TE’ E’ → +TE’ | ε T → FT’ T’→∗FT’ | ε F → ( E ) | id SETS: Lets compute FIRST of F, T, and E and update FIRST of E’ and T’ FIRST(id) = {id} FIRST(∗) = {∗} FIRST(+) = {+} FIRST(() = {(} FIRST()) = {)} FIRST(E’) = {ε} {+, ε} FIRST(T’) = {ε} {∗, ε} FIRST(F) = {(, id} FIRST(T) = FIRST(F) = {(, id} FIRST(E) = FIRST(T) = {(, id} FIRST rules: 1. If X is a terminal, FIRST(X) = {X} 2. If X → ε , then ε ∈ FIRST(X) 3. If X → Y 1 Y 2 • • • Yk * ε and Y 1 • • • Yi-1 ⇒ and a ∈FIRST(Yi) then a ∈ FIRST(X) 74 (Aho, Sethi, Ullman, pp. 189)

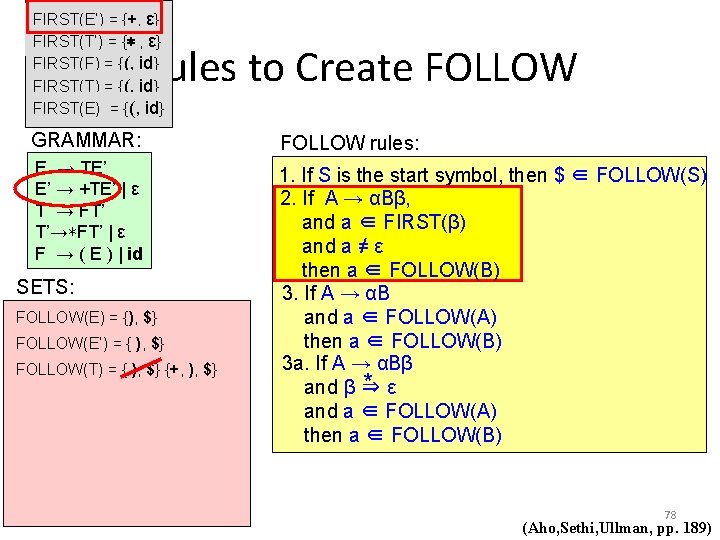
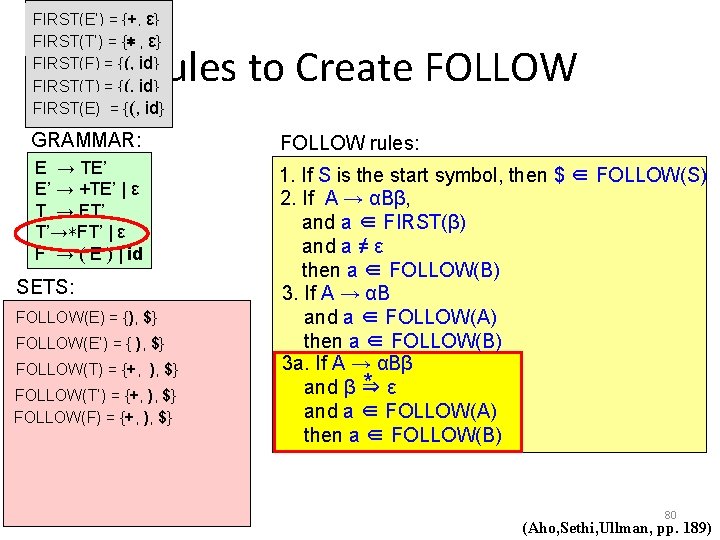
FIRST(E’) = {+, ε} FIRST(T’) = {∗ , ε} FIRST(F) = {(, id} FIRST(T) = {(, id} FIRST(E) = {(, id} Rules to Create FOLLOW GRAMMAR: FOLLOW rules: E → TE’ E’ → +TE’ | ε T → FT’ T’→∗FT’ | ε F → ( E ) | id 1. If S is the start symbol, then $ ∈ FOLLOW(S) 2. If A → αBβ, and a ∈ FIRST(β) and a ≠ ε then a ∈ FOLLOW(B) 3. If A → αB and a ∈ FOLLOW(A) then a ∈ FOLLOW(B) 3 a. If A → αBβ * ε and β ⇒ and a ∈ FOLLOW(A) then a ∈ FOLLOW(B) SETS: FOLLOW(E) = {$} { ), $} FOLLOW(E’) = { ), $} A and B are non-terminals, α and β are strings of grammar symbols 75 (Aho, Sethi, Ullman, pp. 189)

FIRST(E’) = {+, ε} FIRST(T’) = {∗ , ε} FIRST(F) = {(, id} FIRST(T) = {(, id} FIRST(E) = {(, id} Rules to Create FOLLOW GRAMMAR: E → TE’ E’ → +TE’ | ε T → FT’ T’→∗FT’ | ε F → ( E ) | id SETS: FOLLOW(E) = {$} { ), $} FOLLOW(E’) = { ), $} A → α B Y 1 Y 2 Y 3 FOLLOW rules: a ∈ FOLLOW(A) 1. If S is the start symbol, then $ ∈ FOLLOW(S) a ∈ FOLLOW(B) 2. If A → αBβ, and a ∈ FIRST(β) and a ≠ ε then a ∈ FOLLOW(B) 3. If A → αB and a ∈ FOLLOW(A) then a ∈ FOLLOW(B) 3 a. If A → αBβ * ε and β ⇒ and a ∈ FOLLOW(A) then a ∈ FOLLOW(B) A and B are non-terminals, α and β are strings of grammar symbols 76 (Aho, Sethi, Ullman, pp. 189)

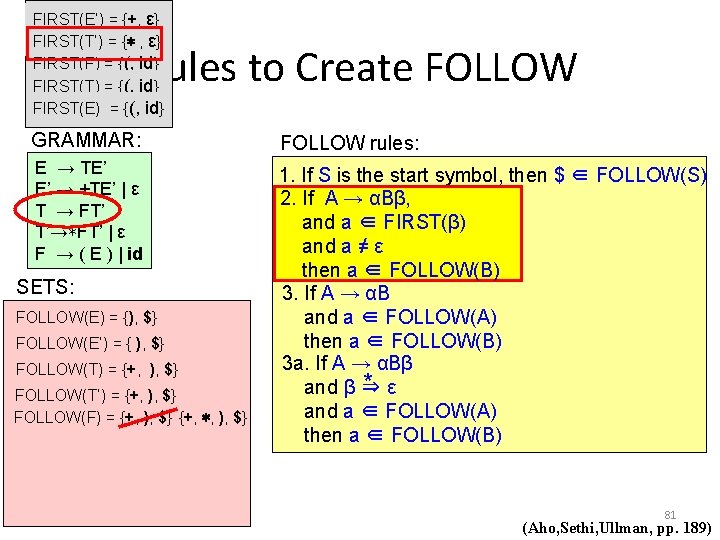
FIRST(E’) = {+, ε} FIRST(T’) = {∗ , ε} FIRST(F) = {(, id} FIRST(T) = {(, id} FIRST(E) = {(, id} Rules to Create FOLLOW GRAMMAR: FOLLOW rules: E → TE’ E’ → +TE’ | ε T → FT’ T’→∗FT’ | ε F → ( E ) | id 1. If S is the start symbol, then $ ∈ FOLLOW(S) 2. If A → αBβ, and a ∈ FIRST(β) and a ≠ ε then a ∈ FOLLOW(B) 3. If A → αB and a ∈ FOLLOW(A) then a ∈ FOLLOW(B) 3 a. If A → αBβ * ε and β ⇒ and a ∈ FOLLOW(A) then a ∈ FOLLOW(B) SETS: FOLLOW(E) = {$} { ), $} FOLLOW(E’) = { ), $} FOLLOW(T) = { ), $} A and B are non-terminals, α and β are strings of grammar symbols 77 (Aho, Sethi, Ullman, pp. 189)

FIRST(E’) = {+, ε} FIRST(T’) = {∗ , ε} FIRST(F) = {(, id} FIRST(T) = {(, id} FIRST(E) = {(, id} Rules to Create FOLLOW GRAMMAR: FOLLOW rules: E → TE’ E’ → +TE’ | ε T → FT’ T’→∗FT’ | ε F → ( E ) | id 1. If S is the start symbol, then $ ∈ FOLLOW(S) 2. If A → αBβ, and a ∈ FIRST(β) and a ≠ ε then a ∈ FOLLOW(B) 3. If A → αB and a ∈ FOLLOW(A) then a ∈ FOLLOW(B) 3 a. If A → αBβ * ε and β ⇒ and a ∈ FOLLOW(A) then a ∈ FOLLOW(B) SETS: FOLLOW(E) = {), $} FOLLOW(E’) = { ), $} FOLLOW(T) = { ), $} {+, ), $} 78 (Aho, Sethi, Ullman, pp. 189)

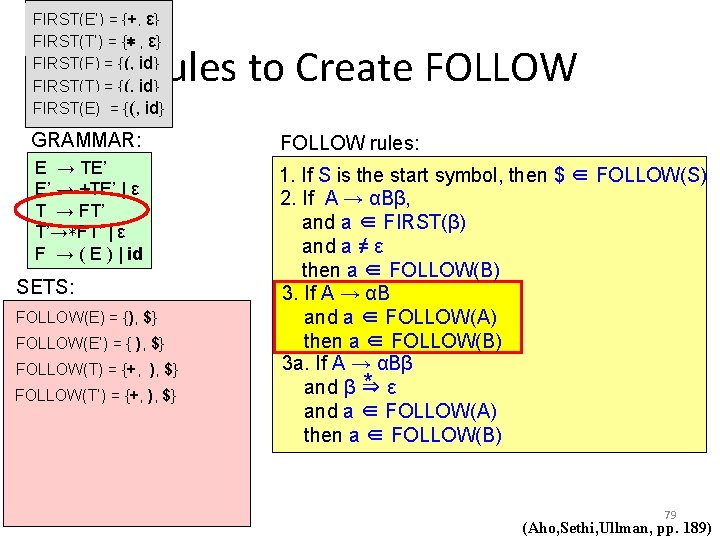
FIRST(E’) = {+, ε} FIRST(T’) = {∗ , ε} FIRST(F) = {(, id} FIRST(T) = {(, id} FIRST(E) = {(, id} Rules to Create FOLLOW GRAMMAR: FOLLOW rules: E → TE’ E’ → +TE’ | ε T → FT’ T’→∗FT’ | ε F → ( E ) | id 1. If S is the start symbol, then $ ∈ FOLLOW(S) 2. If A → αBβ, and a ∈ FIRST(β) and a ≠ ε then a ∈ FOLLOW(B) 3. If A → αB and a ∈ FOLLOW(A) then a ∈ FOLLOW(B) 3 a. If A → αBβ * ε and β ⇒ and a ∈ FOLLOW(A) then a ∈ FOLLOW(B) SETS: FOLLOW(E) = {), $} FOLLOW(E’) = { ), $} FOLLOW(T) = {+, ), $} FOLLOW(T’) = {+, ), $} 79 (Aho, Sethi, Ullman, pp. 189)

FIRST(E’) = {+, ε} FIRST(T’) = {∗ , ε} FIRST(F) = {(, id} FIRST(T) = {(, id} FIRST(E) = {(, id} Rules to Create FOLLOW GRAMMAR: FOLLOW rules: E → TE’ E’ → +TE’ | ε T → FT’ T’→∗FT’ | ε F → ( E ) | id 1. If S is the start symbol, then $ ∈ FOLLOW(S) 2. If A → αBβ, and a ∈ FIRST(β) and a ≠ ε then a ∈ FOLLOW(B) 3. If A → αB and a ∈ FOLLOW(A) then a ∈ FOLLOW(B) 3 a. If A → αBβ * ε and β ⇒ and a ∈ FOLLOW(A) then a ∈ FOLLOW(B) SETS: FOLLOW(E) = {), $} FOLLOW(E’) = { ), $} FOLLOW(T) = {+, ), $} FOLLOW(T’) = {+, ), $} FOLLOW(F) = {+, ), $} 80 (Aho, Sethi, Ullman, pp. 189)

FIRST(E’) = {+, ε} FIRST(T’) = {∗ , ε} FIRST(F) = {(, id} FIRST(T) = {(, id} FIRST(E) = {(, id} Rules to Create FOLLOW GRAMMAR: FOLLOW rules: E → TE’ E’ → +TE’ | ε T → FT’ T’→∗FT’ | ε F → ( E ) | id 1. If S is the start symbol, then $ ∈ FOLLOW(S) 2. If A → αBβ, and a ∈ FIRST(β) and a ≠ ε then a ∈ FOLLOW(B) 3. If A → αB and a ∈ FOLLOW(A) then a ∈ FOLLOW(B) 3 a. If A → αBβ * ε and β ⇒ and a ∈ FOLLOW(A) then a ∈ FOLLOW(B) SETS: FOLLOW(E) = {), $} FOLLOW(E’) = { ), $} FOLLOW(T) = {+, ), $} FOLLOW(T’) = {+, ), $} FOLLOW(F) = {+, ), $} {+, ∗, ), $} 81 (Aho, Sethi, Ullman, pp. 189)

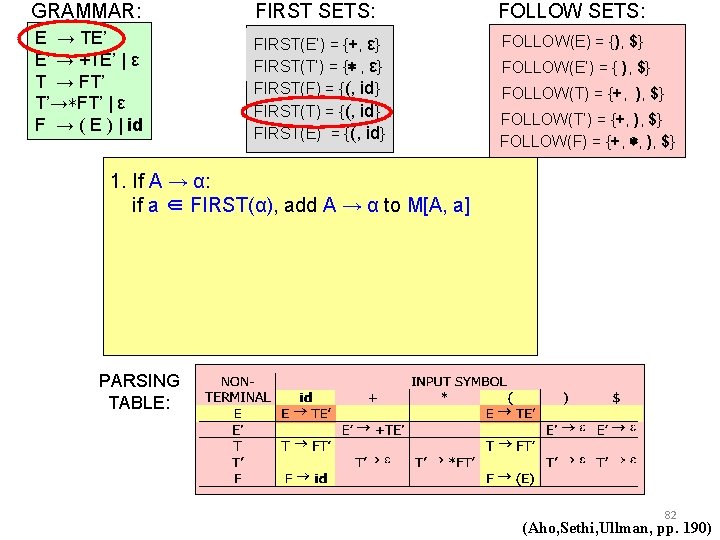
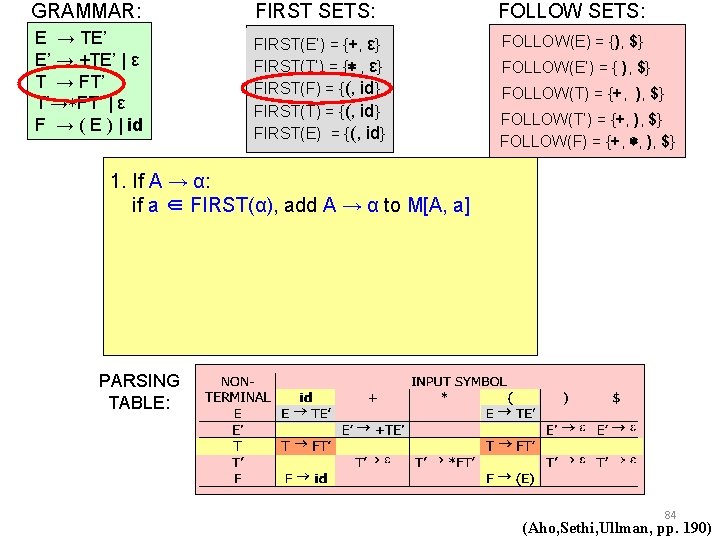
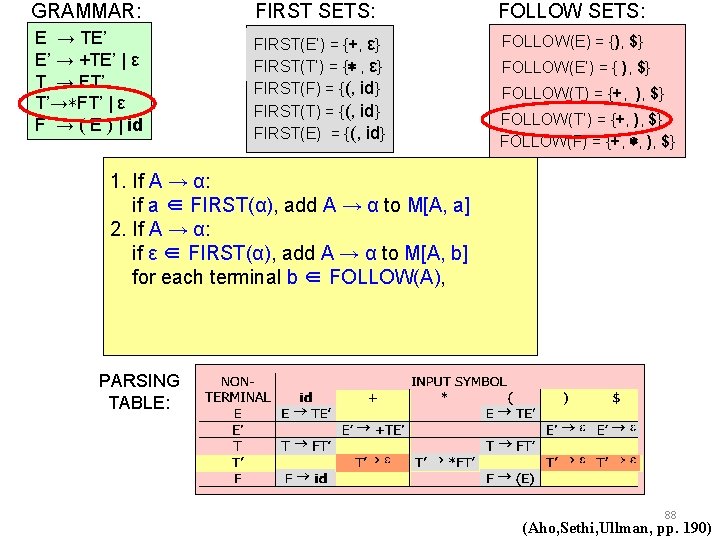
GRAMMAR: FIRST SETS: FOLLOW SETS: E → TE’ E’ → +TE’ | ε T → FT’ T’→∗FT’ | ε F → ( E ) | id FIRST(E’) = {+, ε} FIRST(T’) = {∗ , ε} FIRST(F) = {(, id} FIRST(T) = {(, id} FIRST(E) = {(, id} FOLLOW(E) = {), $} FOLLOW(E’) = { ), $} FOLLOW(T) = {+, ), $} FOLLOW(T’) = {+, ), $} FOLLOW(F) = {+, ∗, ), $} 1. If A → α: if a ∈ FIRST(α), add A → α to M[A, a] PARSING TABLE: 82 (Aho, Sethi, Ullman, pp. 190)

GRAMMAR: FIRST SETS: FOLLOW SETS: E → TE’ E’ → +TE’ | ε T → FT’ T’→∗FT’ | ε F → ( E ) | id FIRST(E’) = {+, ε} FIRST(T’) = {∗ , ε} FIRST(F) = {(, id} FIRST(T) = {(, id} FIRST(E) = {(, id} FOLLOW(E) = {), $} FOLLOW(E’) = { ), $} FOLLOW(T) = {+, ), $} FOLLOW(T’) = {+, ), $} FOLLOW(F) = {+, ∗, ), $} 1. If A → α: if a ∈ FIRST(α), add A → α to M[A, a] PARSING TABLE: 83 (Aho, Sethi, Ullman, pp. 190)

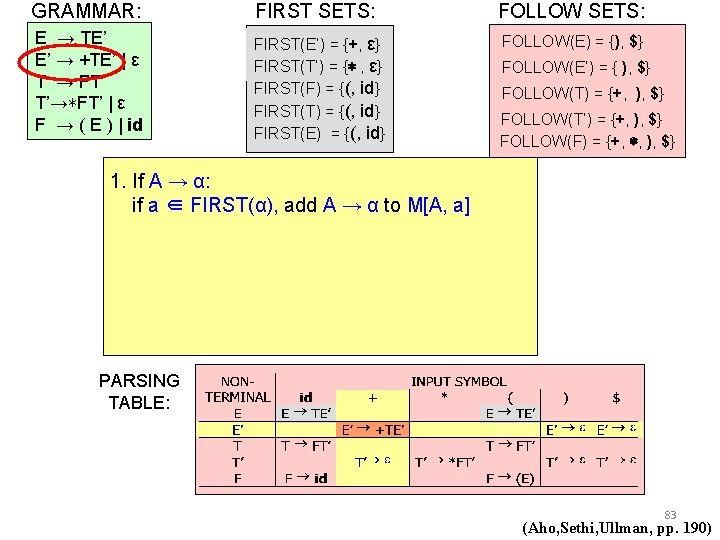
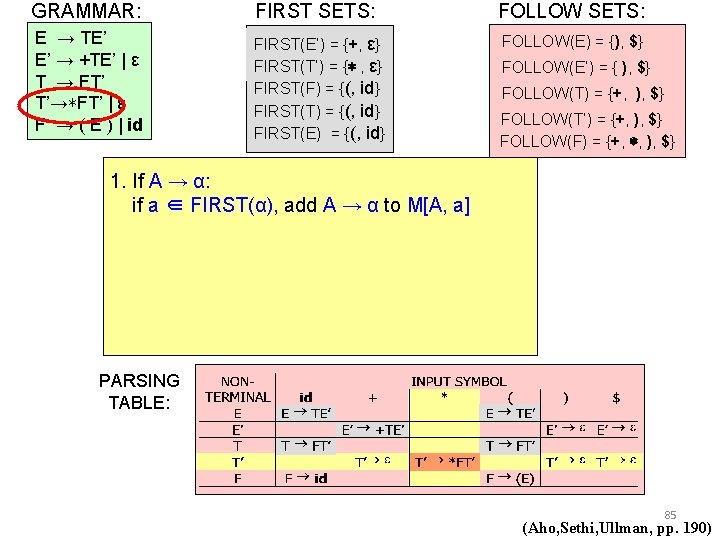
GRAMMAR: FIRST SETS: FOLLOW SETS: E → TE’ E’ → +TE’ | ε T → FT’ T’→∗FT’ | ε F → ( E ) | id FIRST(E’) = {+, ε} FIRST(T’) = {∗ , ε} FIRST(F) = {(, id} FIRST(T) = {(, id} FIRST(E) = {(, id} FOLLOW(E) = {), $} FOLLOW(E’) = { ), $} FOLLOW(T) = {+, ), $} FOLLOW(T’) = {+, ), $} FOLLOW(F) = {+, ∗, ), $} 1. If A → α: if a ∈ FIRST(α), add A → α to M[A, a] PARSING TABLE: 84 (Aho, Sethi, Ullman, pp. 190)

GRAMMAR: FIRST SETS: FOLLOW SETS: E → TE’ E’ → +TE’ | ε T → FT’ T’→∗FT’ | ε F → ( E ) | id FIRST(E’) = {+, ε} FIRST(T’) = {∗ , ε} FIRST(F) = {(, id} FIRST(T) = {(, id} FIRST(E) = {(, id} FOLLOW(E) = {), $} FOLLOW(E’) = { ), $} FOLLOW(T) = {+, ), $} FOLLOW(T’) = {+, ), $} FOLLOW(F) = {+, ∗, ), $} 1. If A → α: if a ∈ FIRST(α), add A → α to M[A, a] PARSING TABLE: 85 (Aho, Sethi, Ullman, pp. 190)

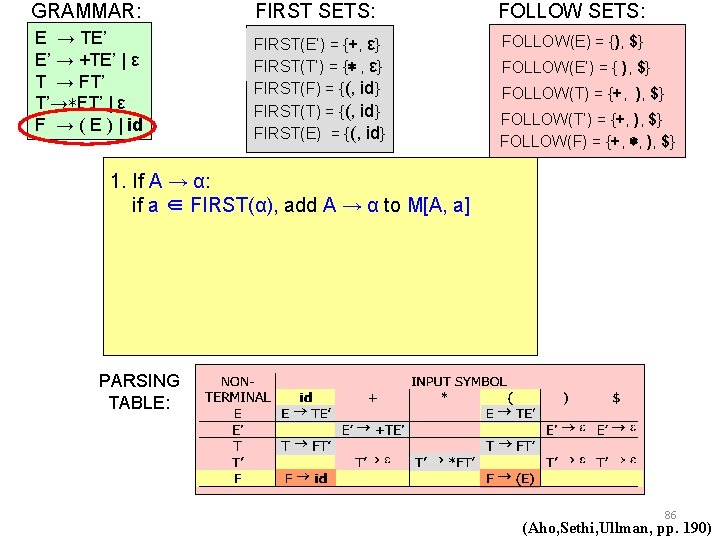
GRAMMAR: FIRST SETS: FOLLOW SETS: E → TE’ E’ → +TE’ | ε T → FT’ T’→∗FT’ | ε F → ( E ) | id FIRST(E’) = {+, ε} FIRST(T’) = {∗ , ε} FIRST(F) = {(, id} FIRST(T) = {(, id} FIRST(E) = {(, id} FOLLOW(E) = {), $} FOLLOW(E’) = { ), $} FOLLOW(T) = {+, ), $} FOLLOW(T’) = {+, ), $} FOLLOW(F) = {+, ∗, ), $} 1. If A → α: if a ∈ FIRST(α), add A → α to M[A, a] PARSING TABLE: 86 (Aho, Sethi, Ullman, pp. 190)

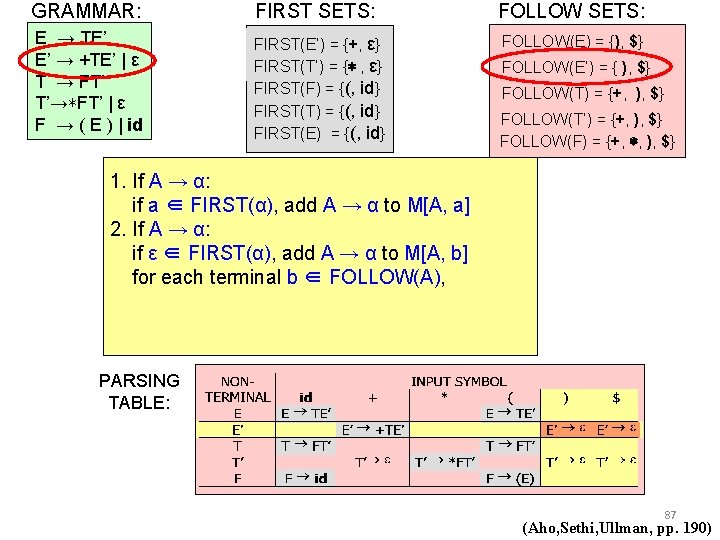
GRAMMAR: FIRST SETS: FOLLOW SETS: E → TE’ E’ → +TE’ | ε T → FT’ T’→∗FT’ | ε F → ( E ) | id FIRST(E’) = {+, ε} FIRST(T’) = {∗ , ε} FIRST(F) = {(, id} FIRST(T) = {(, id} FIRST(E) = {(, id} FOLLOW(E) = {), $} FOLLOW(E’) = { ), $} FOLLOW(T) = {+, ), $} FOLLOW(T’) = {+, ), $} FOLLOW(F) = {+, ∗, ), $} 1. If A → α: if a ∈ FIRST(α), add A → α to M[A, a] 2. If A → α: if ε ∈ FIRST(α), add A → α to M[A, b] for each terminal b ∈ FOLLOW(A), PARSING TABLE: 87 (Aho, Sethi, Ullman, pp. 190)

GRAMMAR: FIRST SETS: FOLLOW SETS: E → TE’ E’ → +TE’ | ε T → FT’ T’→∗FT’ | ε F → ( E ) | id FIRST(E’) = {+, ε} FIRST(T’) = {∗ , ε} FIRST(F) = {(, id} FIRST(T) = {(, id} FIRST(E) = {(, id} FOLLOW(E) = {), $} FOLLOW(E’) = { ), $} FOLLOW(T) = {+, ), $} FOLLOW(T’) = {+, ), $} FOLLOW(F) = {+, ∗, ), $} 1. If A → α: if a ∈ FIRST(α), add A → α to M[A, a] 2. If A → α: if ε ∈ FIRST(α), add A → α to M[A, b] for each terminal b ∈ FOLLOW(A), PARSING TABLE: 88 (Aho, Sethi, Ullman, pp. 190)

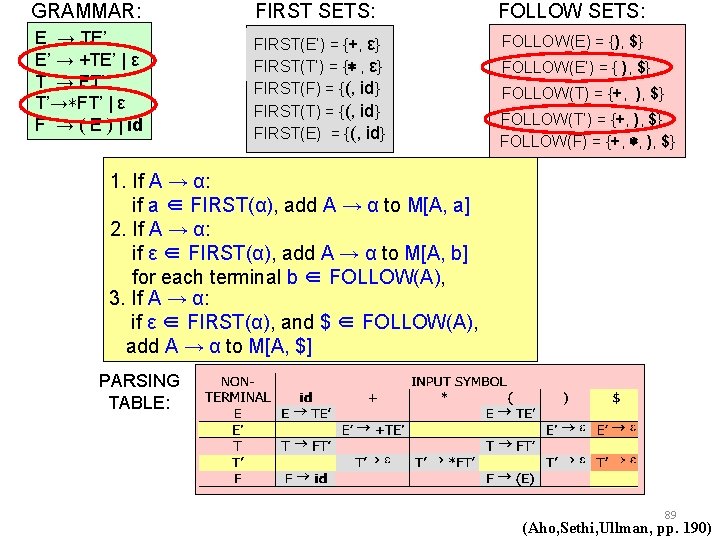
GRAMMAR: FIRST SETS: FOLLOW SETS: E → TE’ E’ → +TE’ | ε T → FT’ T’→∗FT’ | ε F → ( E ) | id FIRST(E’) = {+, ε} FIRST(T’) = {∗ , ε} FIRST(F) = {(, id} FIRST(T) = {(, id} FIRST(E) = {(, id} FOLLOW(E) = {), $} FOLLOW(E’) = { ), $} FOLLOW(T) = {+, ), $} FOLLOW(T’) = {+, ), $} FOLLOW(F) = {+, ∗, ), $} 1. If A → α: if a ∈ FIRST(α), add A → α to M[A, a] 2. If A → α: if ε ∈ FIRST(α), add A → α to M[A, b] for each terminal b ∈ FOLLOW(A), 3. If A → α: if ε ∈ FIRST(α), and $ ∈ FOLLOW(A), add A → α to M[A, $] PARSING TABLE: 89 (Aho, Sethi, Ullman, pp. 190)

Bottom-Up and Top-Down Parsers Top-down parsers: starts constructing the parse tree at the top (root) of the tree and move down towards the leaves. Easy to implement by hand, but work with restricted grammars. example: predictive parsers Bottom-up parsers: build the nodes on the bottom of the parse tree first. Suitable for automatic parser generation, handle a larger class of grammars. examples: shift-reduce parser (or LR(k) parsers) 90 (Aho, Sethi, Ullman, pp. 195)

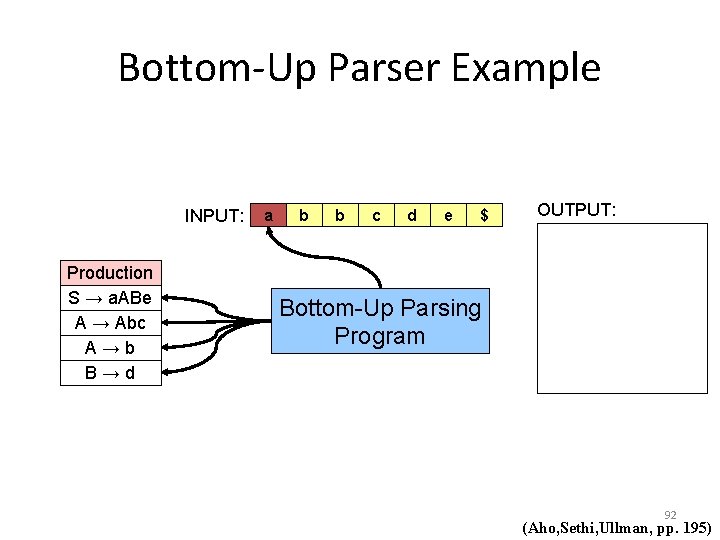
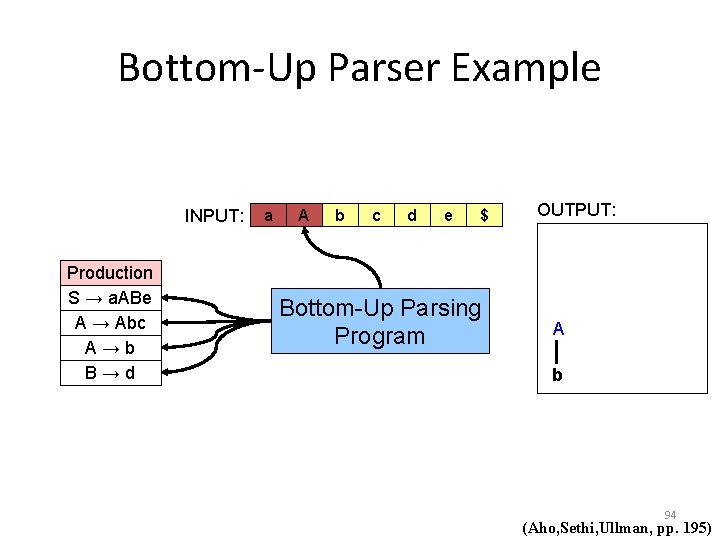
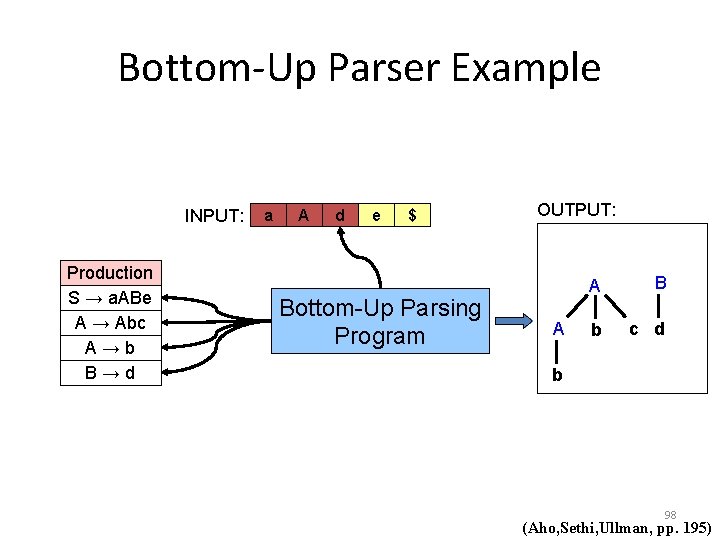
Bottom-Up Parser A bottom-up parser, or a shift-reduce parser, begins at the leaves and works up to the top of the tree. The reduction steps trace a rightmost derivation on reverse. Consider the Grammar: S → a. ABe A → Abc | b B →d We want to parse the input string abbcde. 91 (Aho, Sethi, Ullman, pp. 195)

Bottom-Up Parser Example INPUT: Production S → a. ABe A → Abc A→b B→d a b b c d e $ OUTPUT: Bottom-Up Parsing Program 92 (Aho, Sethi, Ullman, pp. 195)

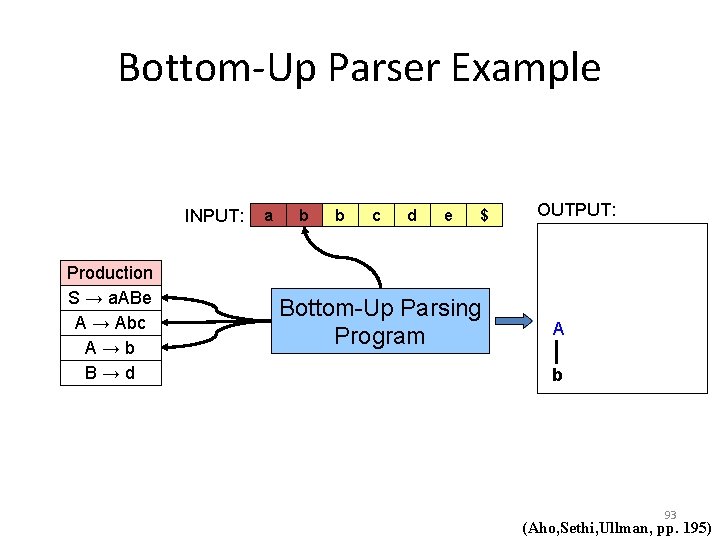
Bottom-Up Parser Example INPUT: Production S → a. ABe A → Abc A→b B→d a b b c d e $ Bottom-Up Parsing Program OUTPUT: A b 93 (Aho, Sethi, Ullman, pp. 195)

Bottom-Up Parser Example INPUT: Production S → a. ABe A → Abc A→b B→d a A b c d e $ Bottom-Up Parsing Program OUTPUT: A b 94 (Aho, Sethi, Ullman, pp. 195)

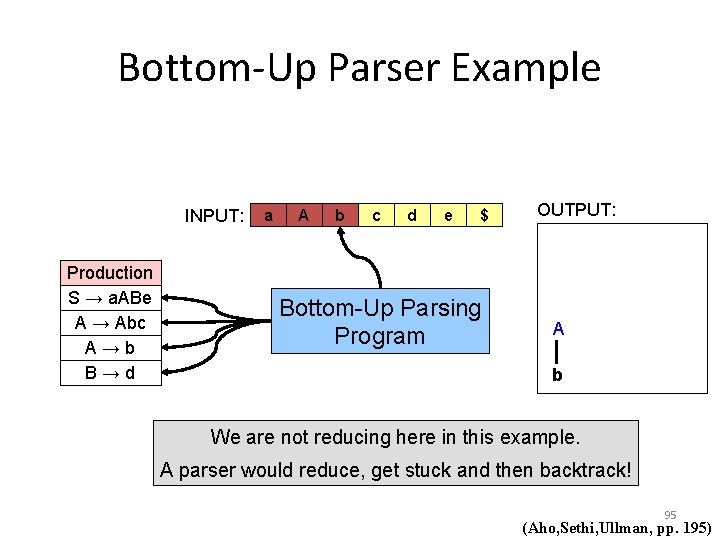
Bottom-Up Parser Example INPUT: Production S → a. ABe A → Abc A→b B→d a A b c d e $ Bottom-Up Parsing Program OUTPUT: A b We are not reducing here in this example. A parser would reduce, get stuck and then backtrack! 95 (Aho, Sethi, Ullman, pp. 195)

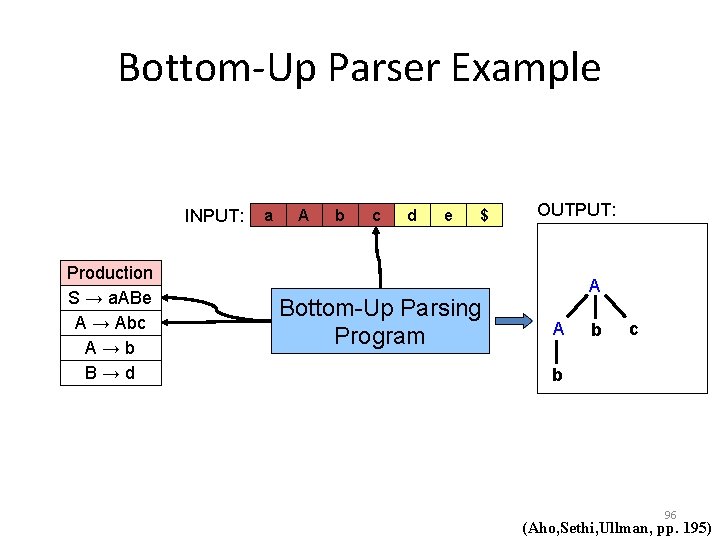
Bottom-Up Parser Example INPUT: Production S → a. ABe A → Abc A→b B→d a A b c d e $ Bottom-Up Parsing Program OUTPUT: A A b c b 96 (Aho, Sethi, Ullman, pp. 195)

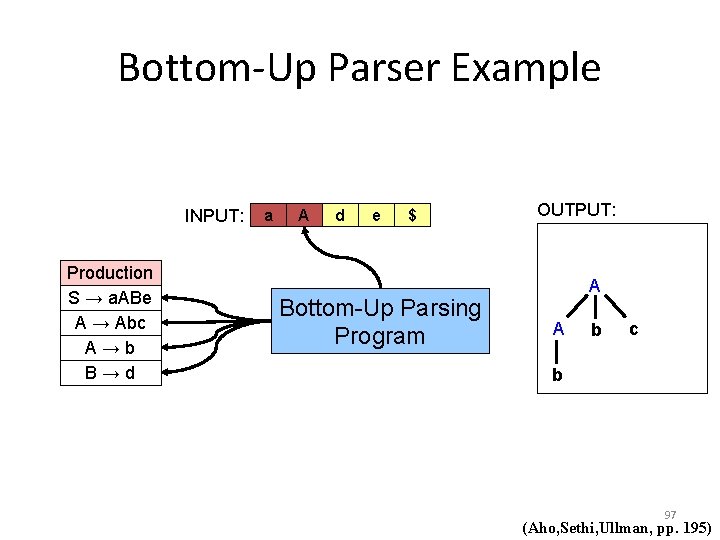
Bottom-Up Parser Example INPUT: Production S → a. ABe A → Abc A→b B→d a A d e $ Bottom-Up Parsing Program OUTPUT: A A b c b 97 (Aho, Sethi, Ullman, pp. 195)

Bottom-Up Parser Example INPUT: Production S → a. ABe A → Abc A→b B→d a A d e $ Bottom-Up Parsing Program OUTPUT: A A B b c d b 98 (Aho, Sethi, Ullman, pp. 195)

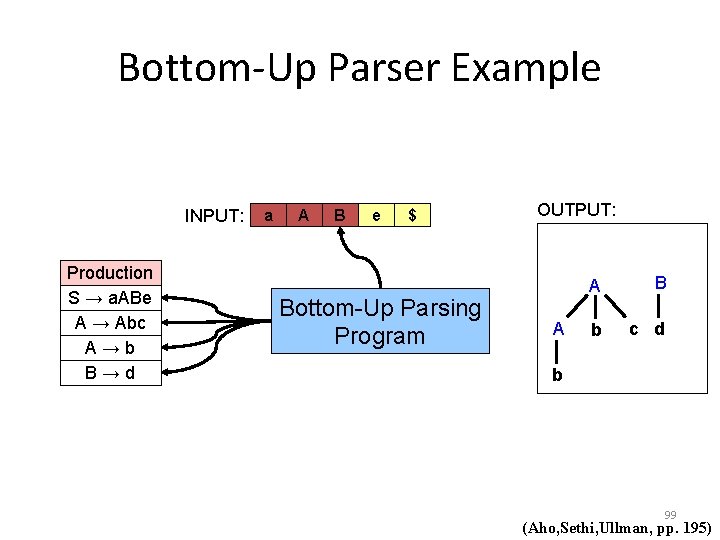
Bottom-Up Parser Example INPUT: Production S → a. ABe A → Abc A→b B→d a A B e $ Bottom-Up Parsing Program OUTPUT: A A B b c d b 99 (Aho, Sethi, Ullman, pp. 195)

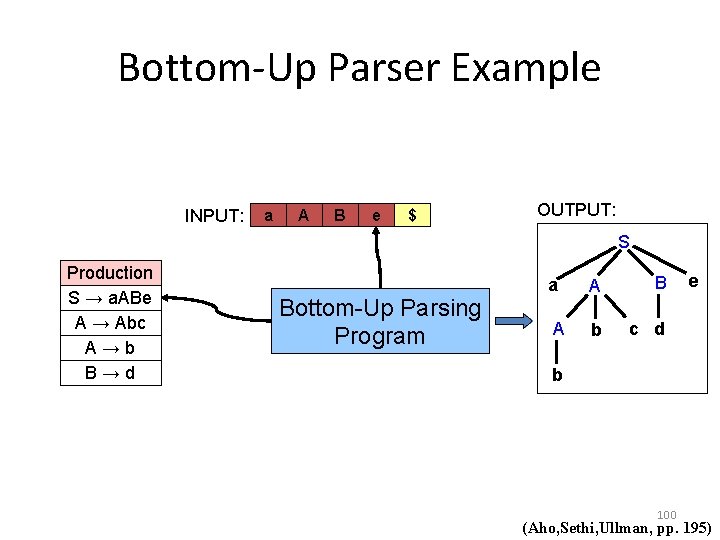
Bottom-Up Parser Example INPUT: a A B e $ OUTPUT: S Production S → a. ABe A → Abc A→b B→d Bottom-Up Parsing Program a A B A b c d e b 100 (Aho, Sethi, Ullman, pp. 195)

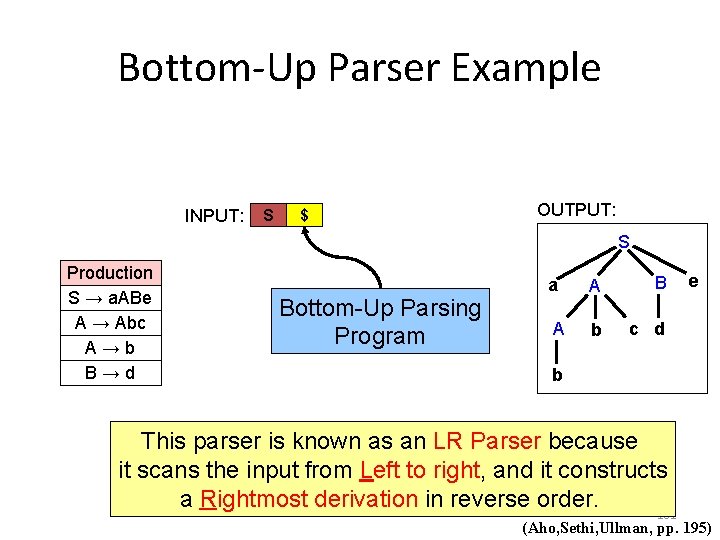
Bottom-Up Parser Example INPUT: S $ OUTPUT: S Production S → a. ABe A → Abc A→b B→d Bottom-Up Parsing Program a A B A b c d e b This parser is known as an LR Parser because it scans the input from Left to right, and it constructs a Rightmost derivation in reverse order. 101 (Aho, Sethi, Ullman, pp. 195)

Bottom-Up Parser Example The scanning of productions for matching with handles in the input string, and backtracking, makes the method used in the previous example very inneficient. Can we do better? 102

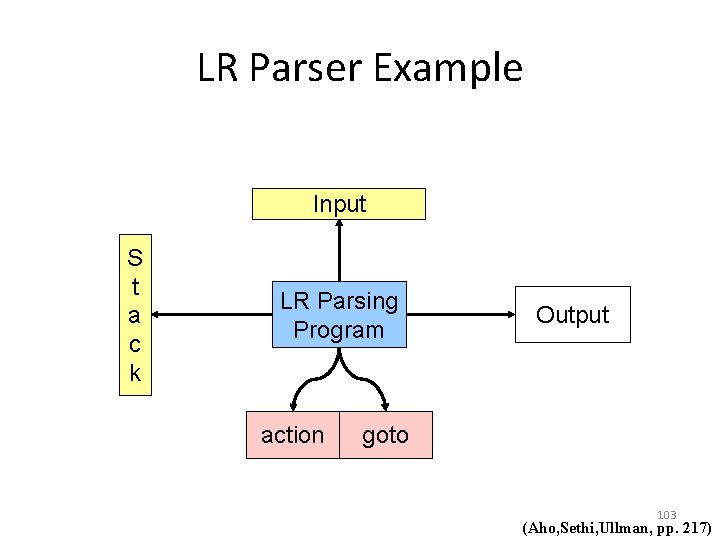
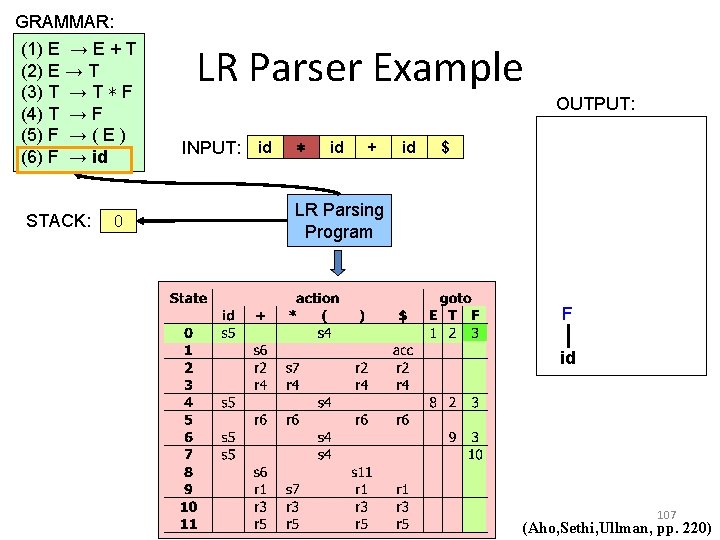
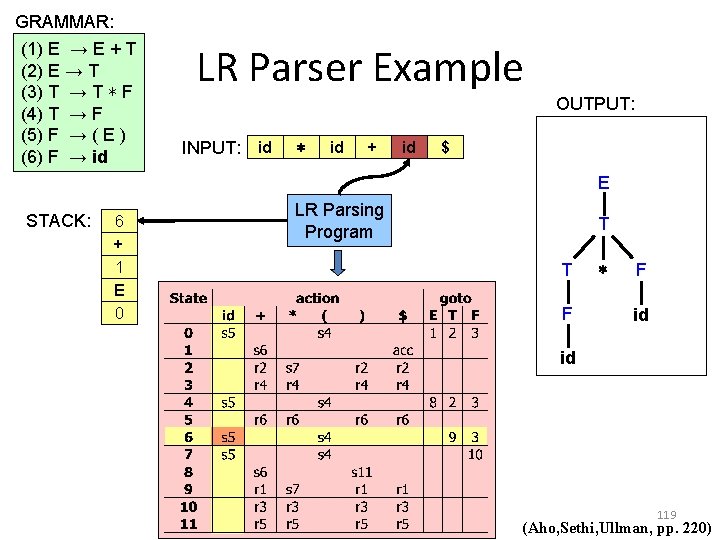
LR Parser Example Input S t a c k LR Parsing Program action Output goto 103 (Aho, Sethi, Ullman, pp. 217)

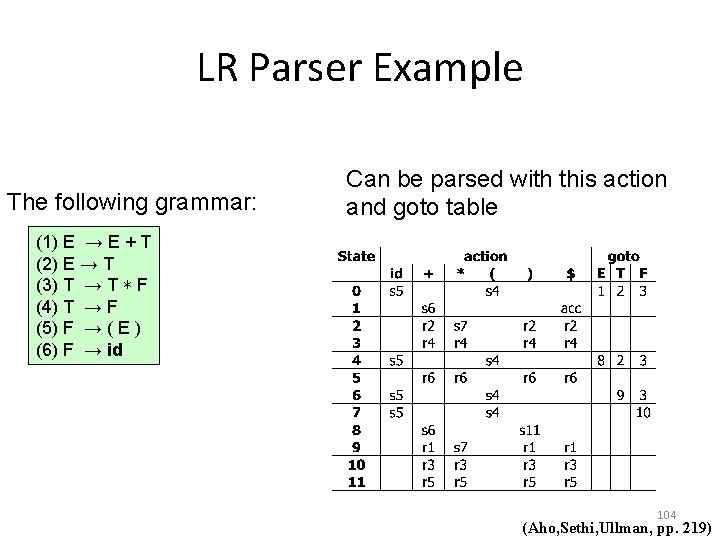
LR Parser Example The following grammar: Can be parsed with this action and goto table (1) E → E + T (2) E → T (3) T → T ∗ F (4) T → F (5) F → ( E ) (6) F → id 104 (Aho, Sethi, Ullman, pp. 219)

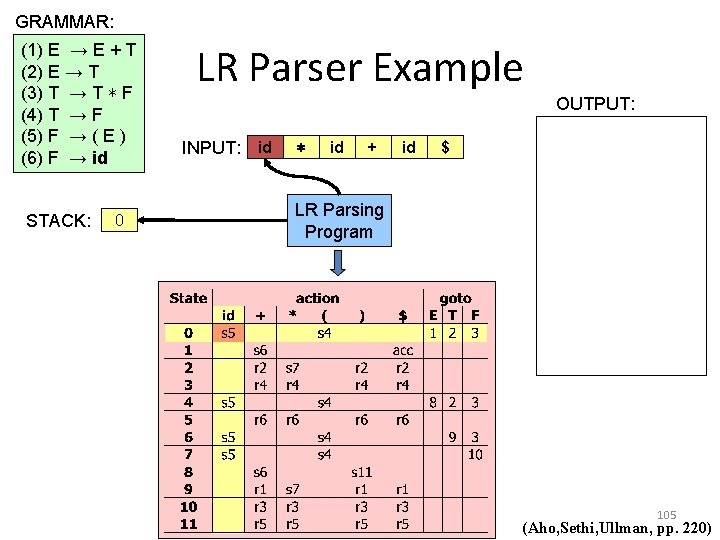
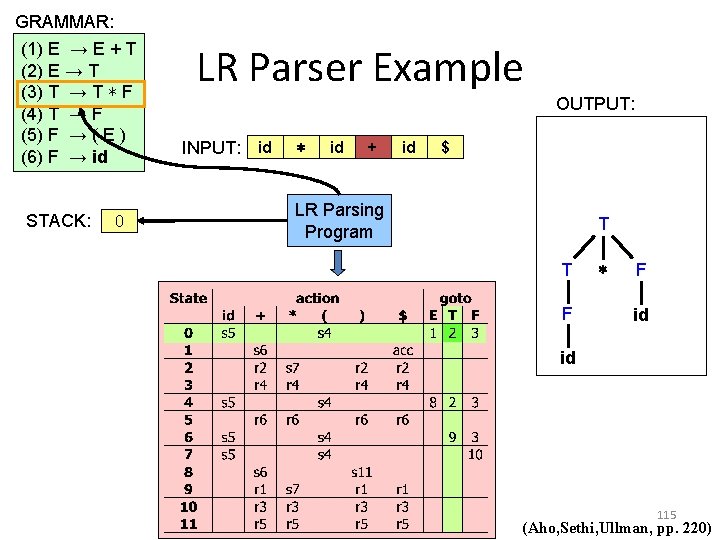
GRAMMAR: (1) E → E + T (2) E → T (3) T → T ∗ F (4) T → F (5) F → ( E ) (6) F → id STACK: E 0 LR Parser Example OUTPUT: INPUT: id ∗ id + id $ LR Parsing Program 105 (Aho, Sethi, Ullman, pp. 220)

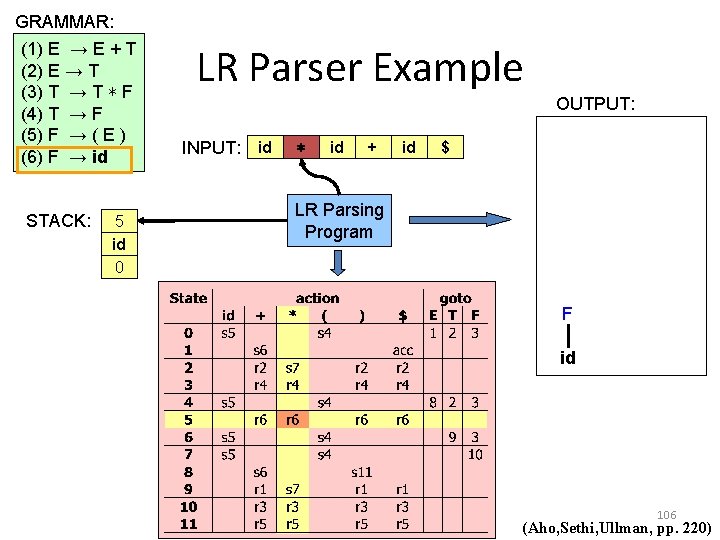
GRAMMAR: (1) E → E + T (2) E → T (3) T → T ∗ F (4) T → F (5) F → ( E ) (6) F → id STACK: E 5 id 0 LR Parser Example OUTPUT: INPUT: id ∗ id + id $ LR Parsing Program F id 106 (Aho, Sethi, Ullman, pp. 220)

GRAMMAR: (1) E → E + T (2) E → T (3) T → T ∗ F (4) T → F (5) F → ( E ) (6) F → id STACK: 0 LR Parser Example OUTPUT: INPUT: id ∗ id + id $ LR Parsing Program F id 107 (Aho, Sethi, Ullman, pp. 220)

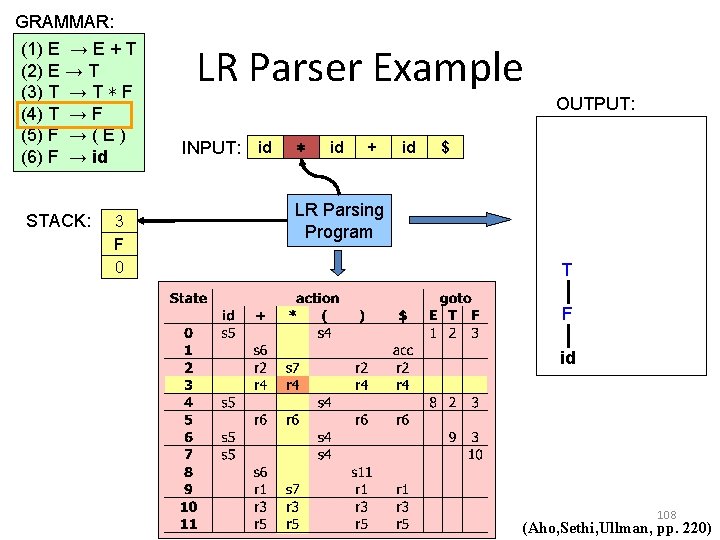
GRAMMAR: (1) E → E + T (2) E → T (3) T → T ∗ F (4) T → F (5) F → ( E ) (6) F → id STACK: E 3 F 0 LR Parser Example OUTPUT: INPUT: id ∗ id + id $ LR Parsing Program T F id 108 (Aho, Sethi, Ullman, pp. 220)

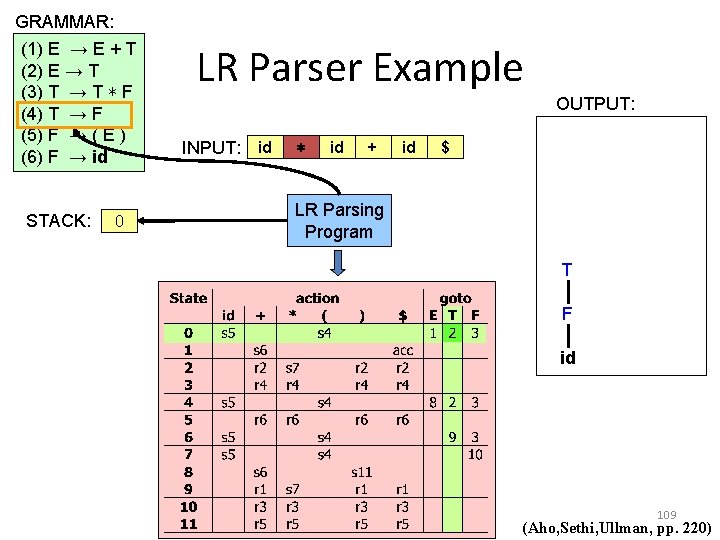
GRAMMAR: (1) E → E + T (2) E → T (3) T → T ∗ F (4) T → F (5) F → ( E ) (6) F → id STACK: 0 LR Parser Example OUTPUT: INPUT: id ∗ id + id $ LR Parsing Program T F id 109 (Aho, Sethi, Ullman, pp. 220)

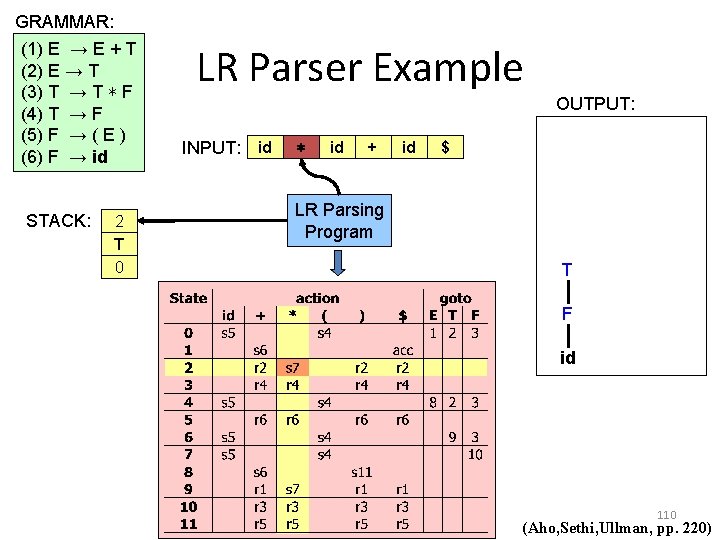
GRAMMAR: (1) E → E + T (2) E → T (3) T → T ∗ F (4) T → F (5) F → ( E ) (6) F → id STACK: E 2 T 0 LR Parser Example OUTPUT: INPUT: id ∗ id + id $ LR Parsing Program T F id 110 (Aho, Sethi, Ullman, pp. 220)

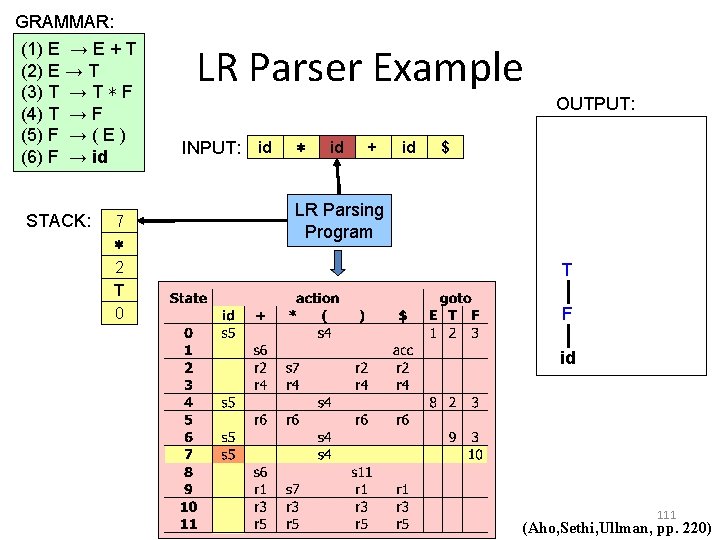
GRAMMAR: (1) E → E + T (2) E → T (3) T → T ∗ F (4) T → F (5) F → ( E ) (6) F → id STACK: E 7 ∗ 2 T 0 LR Parser Example OUTPUT: INPUT: id ∗ id + id $ LR Parsing Program T F id 111 (Aho, Sethi, Ullman, pp. 220)

GRAMMAR: (1) E → E + T (2) E → T (3) T → T ∗ F (4) T → F (5) F → ( E ) (6) F → id STACK: E 5 id 7 ∗ 2 T 0 LR Parser Example OUTPUT: INPUT: id ∗ id + id $ LR Parsing Program T F F id id 112 (Aho, Sethi, Ullman, pp. 220)

GRAMMAR: (1) E → E + T (2) E → T (3) T → T ∗ F (4) T → F (5) F → ( E ) (6) F → id STACK: E 7 ∗ 2 T 0 LR Parser Example OUTPUT: INPUT: id ∗ id + id $ LR Parsing Program T F F id id 113 (Aho, Sethi, Ullman, pp. 220)

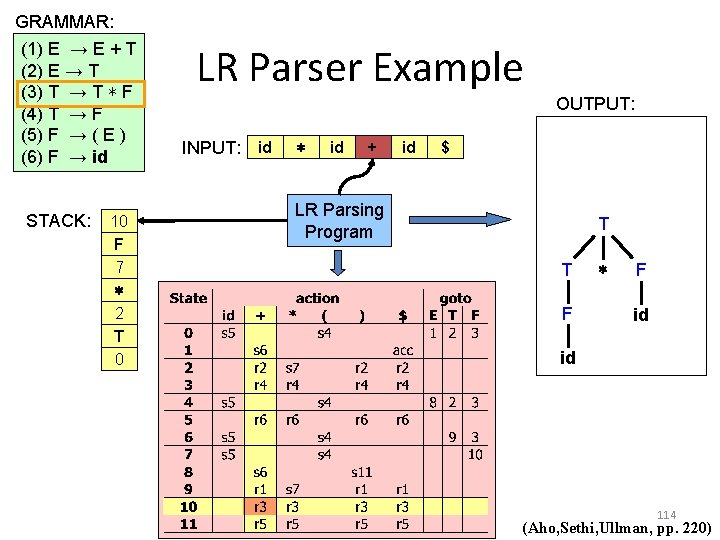
GRAMMAR: (1) E → E + T (2) E → T (3) T → T ∗ F (4) T → F (5) F → ( E ) (6) F → id STACK: 10 E F 7 ∗ 2 T 0 LR Parser Example OUTPUT: INPUT: id ∗ id + id $ LR Parsing Program T T F ∗ F id id 114 (Aho, Sethi, Ullman, pp. 220)

GRAMMAR: (1) E → E + T (2) E → T (3) T → T ∗ F (4) T → F (5) F → ( E ) (6) F → id STACK: 0 LR Parser Example OUTPUT: INPUT: id ∗ id + id $ LR Parsing Program T T F ∗ F id id 115 (Aho, Sethi, Ullman, pp. 220)

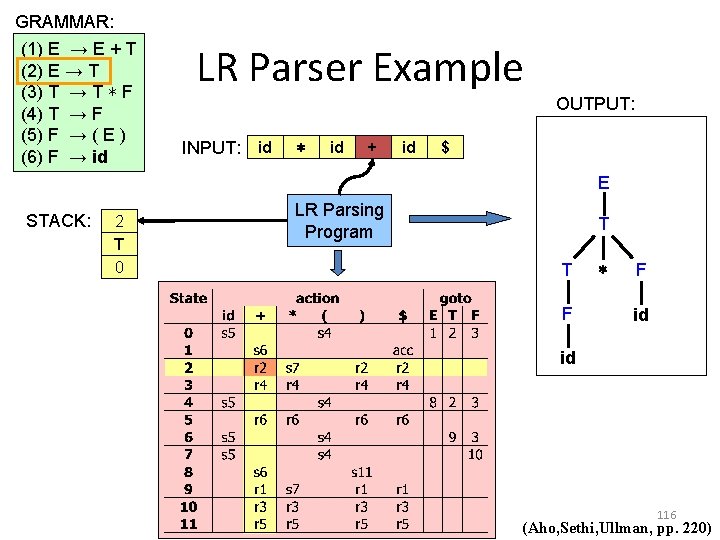
GRAMMAR: (1) E → E + T (2) E → T (3) T → T ∗ F (4) T → F (5) F → ( E ) (6) F → id LR Parser Example OUTPUT: INPUT: id ∗ id + id $ E STACK: 2 T 0 LR Parsing Program T T F ∗ F id id 116 (Aho, Sethi, Ullman, pp. 220)

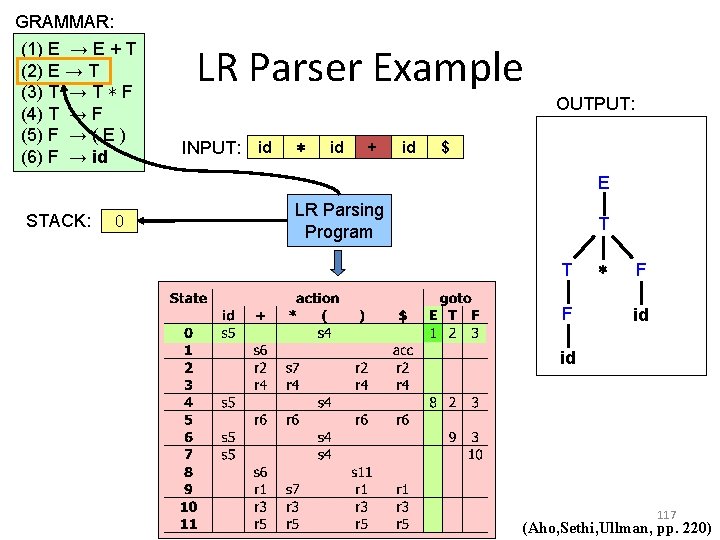
GRAMMAR: (1) E → E + T (2) E → T (3) T → T ∗ F (4) T → F (5) F → ( E ) (6) F → id LR Parser Example OUTPUT: INPUT: id ∗ id + id $ E STACK: 0 LR Parsing Program T T F ∗ F id id 117 (Aho, Sethi, Ullman, pp. 220)

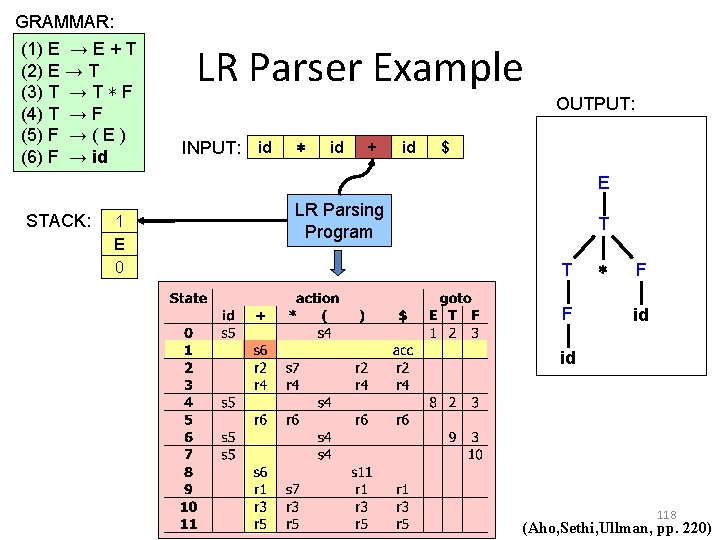
GRAMMAR: (1) E → E + T (2) E → T (3) T → T ∗ F (4) T → F (5) F → ( E ) (6) F → id LR Parser Example OUTPUT: INPUT: id ∗ id + id $ E STACK: 1 E 0 LR Parsing Program T T F ∗ F id id 118 (Aho, Sethi, Ullman, pp. 220)

GRAMMAR: (1) E → E + T (2) E → T (3) T → T ∗ F (4) T → F (5) F → ( E ) (6) F → id LR Parser Example OUTPUT: INPUT: id ∗ id + id $ E STACK: 6 + 1 E 0 LR Parsing Program T T F ∗ F id id 119 (Aho, Sethi, Ullman, pp. 220)

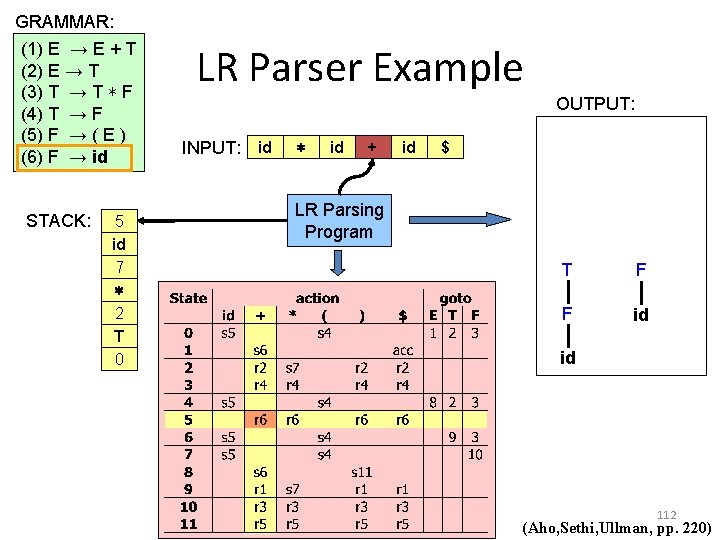
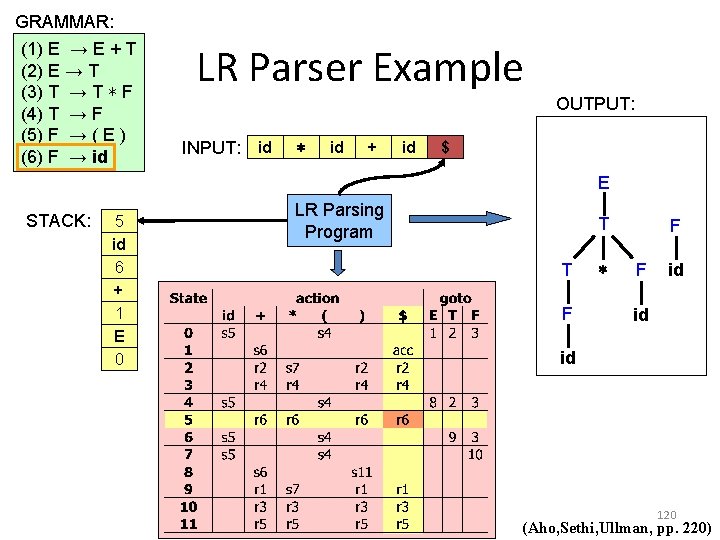
GRAMMAR: (1) E → E + T (2) E → T (3) T → T ∗ F (4) T → F (5) F → ( E ) (6) F → id LR Parser Example OUTPUT: INPUT: id ∗ id + id $ E STACK: 5 id 6 + 1 E 0 LR Parsing Program T T F ∗ F F id id id 120 (Aho, Sethi, Ullman, pp. 220)

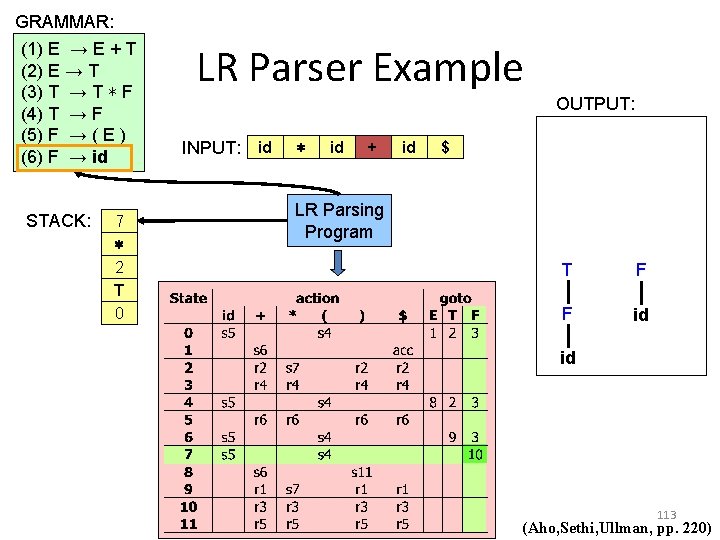
GRAMMAR: (1) E → E + T (2) E → T (3) T → T ∗ F (4) T → F (5) F → ( E ) (6) F → id LR Parser Example OUTPUT: INPUT: id ∗ id + id $ E STACK: 6 + 1 E 0 LR Parsing Program T T F ∗ F F id id id 121 (Aho, Sethi, Ullman, pp. 220)

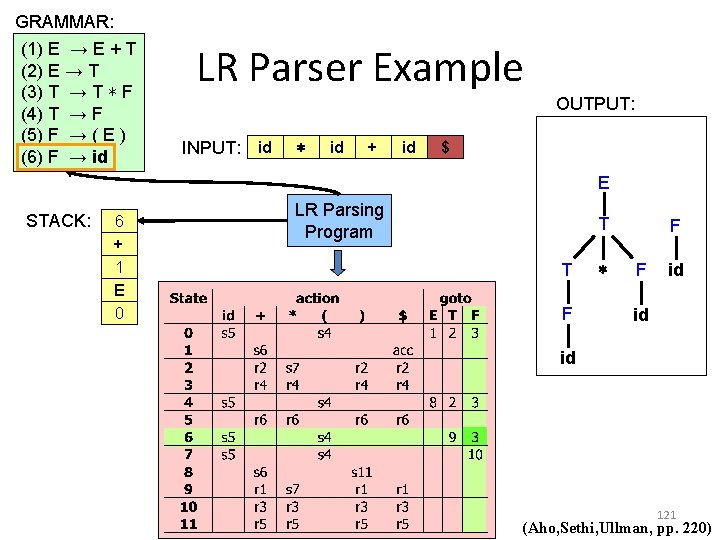
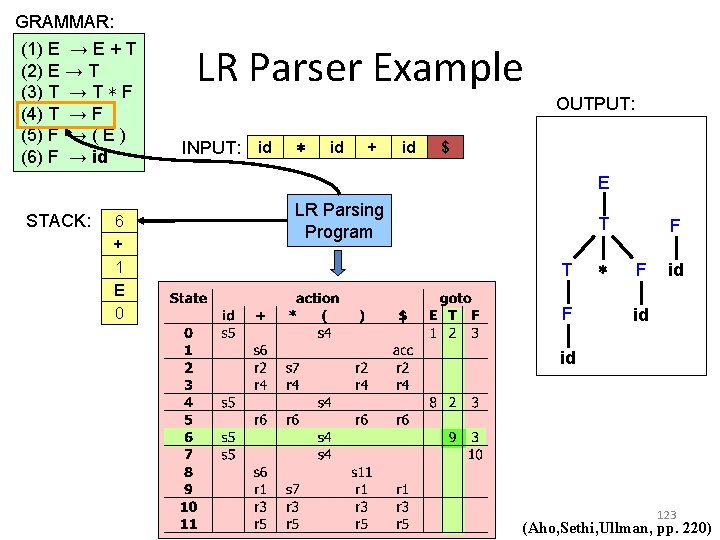
GRAMMAR: (1) E → E + T (2) E → T (3) T → T ∗ F (4) T → F (5) F → ( E ) (6) F → id STACK: 3 F 6 + 1 E 0 LR Parser Example OUTPUT: INPUT: id ∗ id + id $ LR Parsing Program T F E T T F ∗ F id id id 122 (Aho, Sethi, Ullman, pp. 220)

GRAMMAR: (1) E → E + T (2) E → T (3) T → T ∗ F (4) T → F (5) F → ( E ) (6) F → id LR Parser Example OUTPUT: INPUT: id ∗ id + id $ E STACK: 6 + 1 E 0 LR Parsing Program T T F ∗ F F id id id 123 (Aho, Sethi, Ullman, pp. 220)

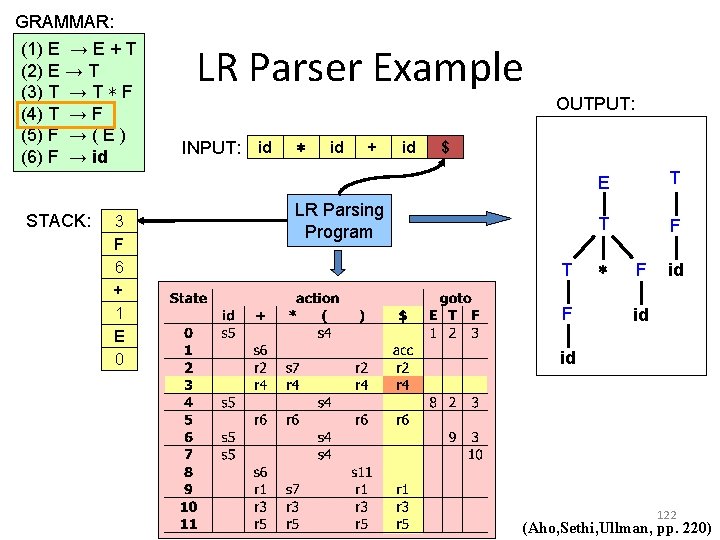
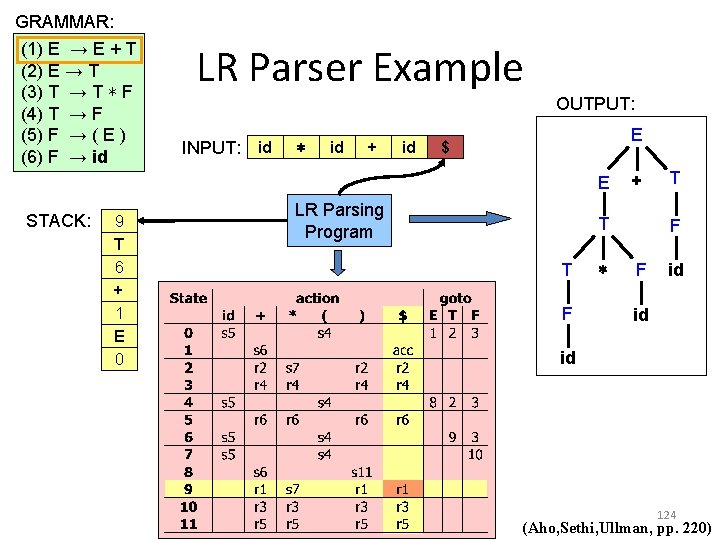
GRAMMAR: (1) E → E + T (2) E → T (3) T → T ∗ F (4) T → F (5) F → ( E ) (6) F → id LR Parser Example OUTPUT: INPUT: id ∗ id + id E $ E STACK: 9 T 6 + 1 E 0 LR Parsing Program + T T F ∗ T F F id id id 124 (Aho, Sethi, Ullman, pp. 220)

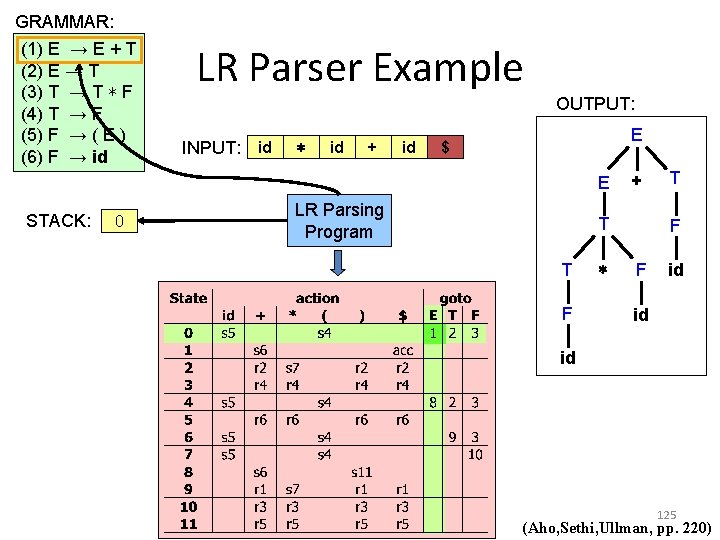
GRAMMAR: (1) E → E + T (2) E → T (3) T → T ∗ F (4) T → F (5) F → ( E ) (6) F → id LR Parser Example OUTPUT: INPUT: id ∗ id + id E $ E STACK: 0 LR Parsing Program + T T F ∗ T F F id id id 125 (Aho, Sethi, Ullman, pp. 220)

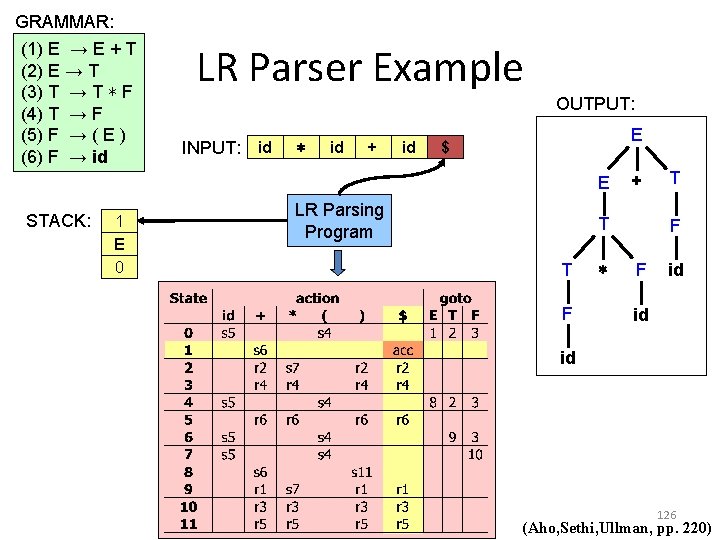
GRAMMAR: (1) E → E + T (2) E → T (3) T → T ∗ F (4) T → F (5) F → ( E ) (6) F → id LR Parser Example OUTPUT: INPUT: id ∗ id + id E $ E STACK: 1 E 0 LR Parsing Program + T T F ∗ T F F id id id 126 (Aho, Sethi, Ullman, pp. 220)

Constructing Parsing Tables All LR parsers use the same parsing program that we demonstrated in the previous slides. What differentiates the LR parsers are the action and the goto tables: Simple LR (SLR): succeds for the fewest grammars, but is the easiest to implement. (See Aho. Sethi. Ullman pp. 221 -230). Canonical LR: succeds for the most grammars, but is the hardest to implement. It splits states when necessary to prevent reductions that would get the parser stuck. (See Aho. Sethi. Ullman pp. 230 -236). Lookahead LR (LALR): succeds for most common syntatic constructions used in programming languages, but produces LR tables much smaller than canonical LR. (See Aho. Sethi. Ullman pp. 236 -247). 127 (Aho, Sethi, Ullman, pp. 221)

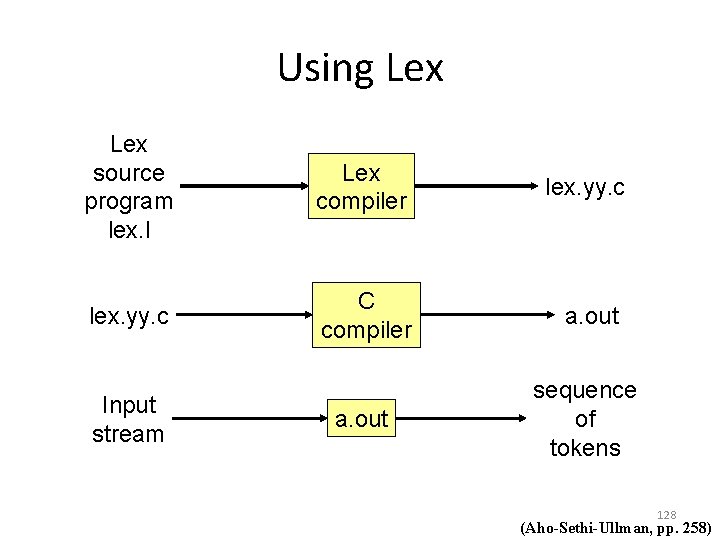
Using Lex source program lex. l Lex compiler lex. yy. c C compiler a. out sequence of tokens Input stream 128 (Aho-Sethi-Ullman, pp. 258)

Parsing Action Conflicts If the grammar specified is ambiguous, yacc will report parsing action conflicts. These conflicts can be reduce/reduce conflicts or shift/reduce conflicts. Yacc has rules to resolve such conflicts automatically (see Aho. Sethi. Ullman, pp. 262 -264), but the resulting parser might not have the behavior intended by the grammar writer. . Whenever you see a conflict report, rerun yacc with the -v flag, examine the y. output file, and re-write your grammar to eliminate the conflicts. 129 (Aho-Sethi-Ullman, pp. 262)

Three-Address Statements A popular form of intermediate code used in optimizing compilers is threeaddress statements (or variations, such as quadruples). Source statement: x=a+b∗ c+d Three address statements with temporaries t 1 and t 2: t 1 = b ∗ c t 2 = a + t 1 x = t 2 + d 130 (Aho-Sethi-Ullman, pp. 466)

Intermediate Code Generation Reading List: Aho-Sethi-Ullman: Chapter 8. 1 ~ 8. 3, Chapter 8. 7 131

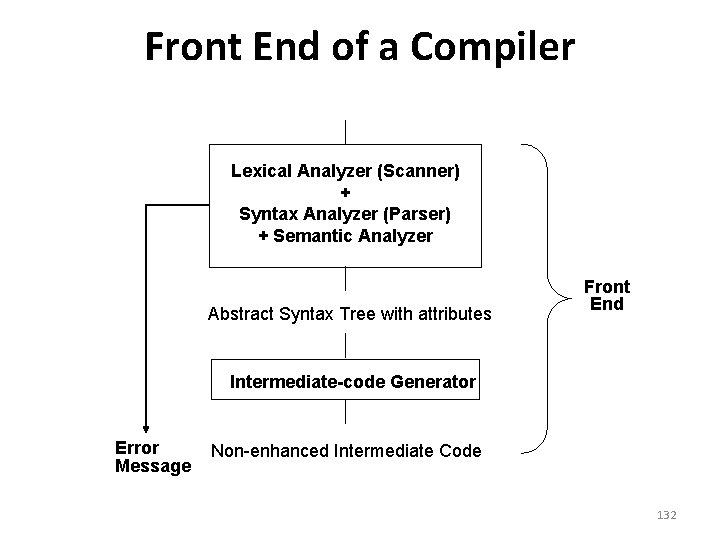
Front End of a Compiler Lexical Analyzer (Scanner) + Syntax Analyzer (Parser) + Semantic Analyzer Abstract Syntax Tree with attributes Front End Intermediate-code Generator Error Message Non-enhanced Intermediate Code 132

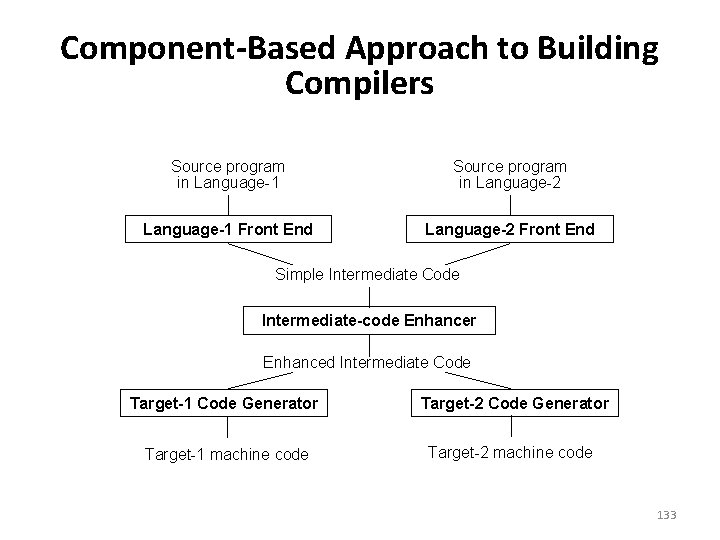
Component-Based Approach to Building Compilers Source program in Language-1 Source program in Language-2 Language-1 Front End Language-2 Front End Simple Intermediate Code Intermediate-code Enhancer Enhanced Intermediate Code Target-1 Code Generator Target-2 Code Generator Target-1 machine code Target-2 machine code 133

Advantages of Using an Intermediate Language 1. Retargeting - Build a compiler for a new machine by attaching a new code generator to an existing frontend. 2. Code Improvements - reuse intermediate code improvements in compilers for different languages and different machines. Note: the terms “intermediate code”, “intermediate language”, and “intermediate representation” are all used interchangeably. 134

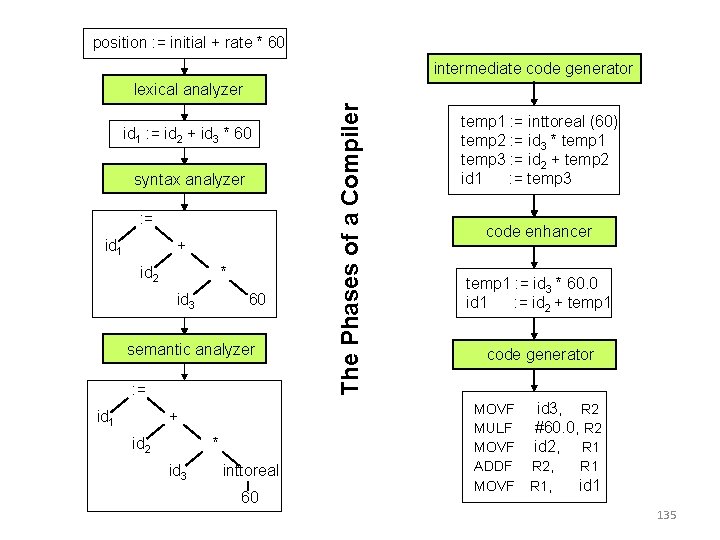
position : = initial + rate * 60 intermediate code generator id 1 : = id 2 + id 3 * 60 syntax analyzer : = id 1 + id 2 * id 3 60 semantic analyzer : = id 1 + id 2 * id 3 inttoreal 60 The Phases of a Compiler lexical analyzer temp 1 : = inttoreal (60) temp 2 : = id 3 * temp 1 temp 3 : = id 2 + temp 2 id 1 : = temp 3 code enhancer temp 1 : = id 3 * 60. 0 id 1 : = id 2 + temp 1 code generator MOVF MULF MOVF ADDF MOVF id 3, R 2 #60. 0, R 2 id 2, R 1 R 2, R 1, R 1 id 1 135