Chapter 6 The Vorticity Equation for a Homogeneous

Chapter 6 The Vorticity Equation for a Homogeneous Fluid – Planetary waves

The vorticity equation for a layer of homogeneous fluid of variable depth H(x, y, t) u(x, y, t) x horizontal momentum equations

Cross-differentiation Continuity equation Integrate with respect to height Assume u and v to be functions of x and y only

Use the identity The quantity (f + z)/H is called the potential vorticity for a homogeneous fluid. It is conserved following a fluid column.

Planetary, or Rossby Waves Ø The atmosphere is a complex dynamical system which can support many different kinds of wave motion covering a wide range of time and space scales. Ø One of the most important wave types as far as the largescale circulation of the atmosphere is concerned is the planetary wave, or Rossby wave. Ø These are prominent in hemispheric synoptic charts; either isobaric charts at mean sea level (msl) or upper level charts of the geopotential height of isobaric surfaces, e. g. , 500 mb.

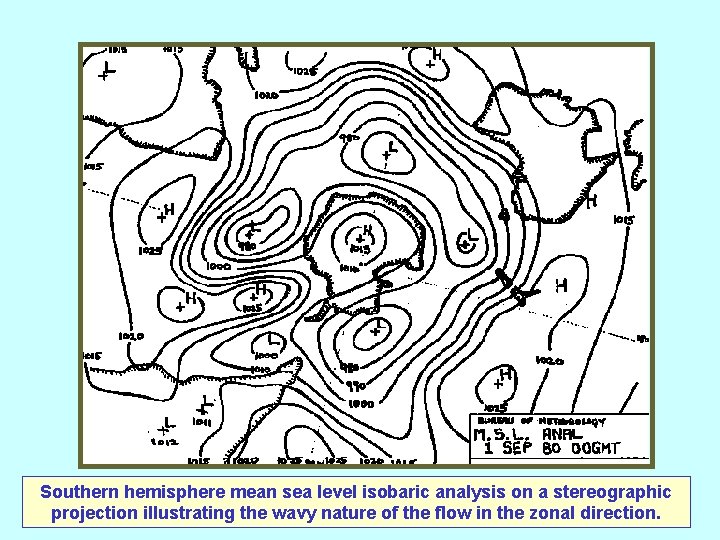
Southern hemisphere mean sea level isobaric analysis on a stereographic projection illustrating the wavy nature of the flow in the zonal direction.

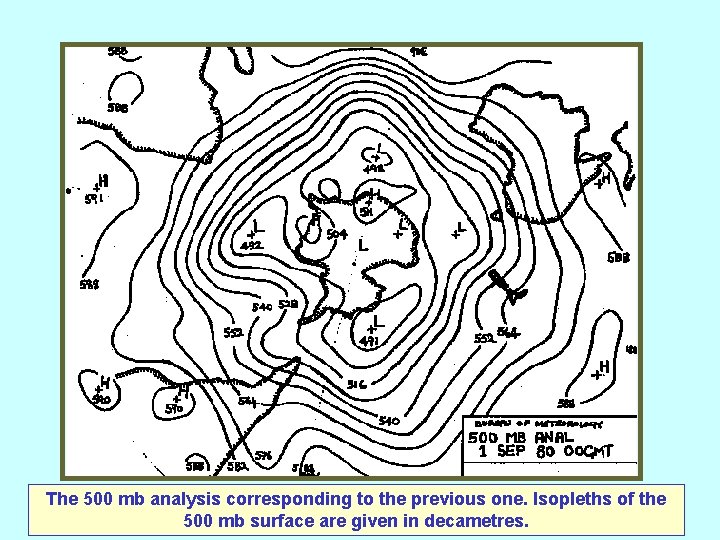
The 500 mb analysis corresponding to the previous one. Isopleths of the 500 mb surface are given in decametres.

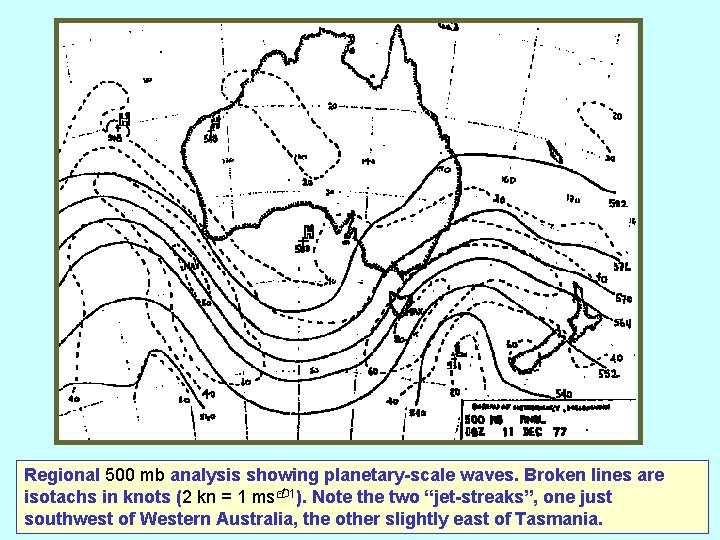
Regional 500 mb analysis showing planetary-scale waves. Broken lines are isotachs in knots (2 kn = 1 ms-1). Note the two “jet-streaks”, one just southwest of Western Australia, the other slightly east of Tasmania.

Planetary Waves are Inertial Waves Ø A planetary wave in its pure form is a type of inertial wave which owes its existence to the variation of the Coriolis parameter with latitude. Ø An inertial wave is one in which energy transfer is between the kinetic energy of relative motion and kinetic energy of absolute motion. Ø Such waves may be studied within the framework of the Cartesian equations described above by making the socalled "beta-plane" or "b-plane" approximation.

The beta-plane approximation Ø This approximation regards f as a linear function of the north-south direction y, i. e. , f = f 0 + by, where b is a positive constant, so that the effect of the variation of the Coriolis parameter with latitude is incorporated in the vorticity equation. Ø The beta-plane approximation allows us to study of the effects of varying f with latitude without the added complication of working in spherical geometry. Ø At the equator, f 0 = 0 whereupon f = by. We call this an equatorial beta-plane approximation.

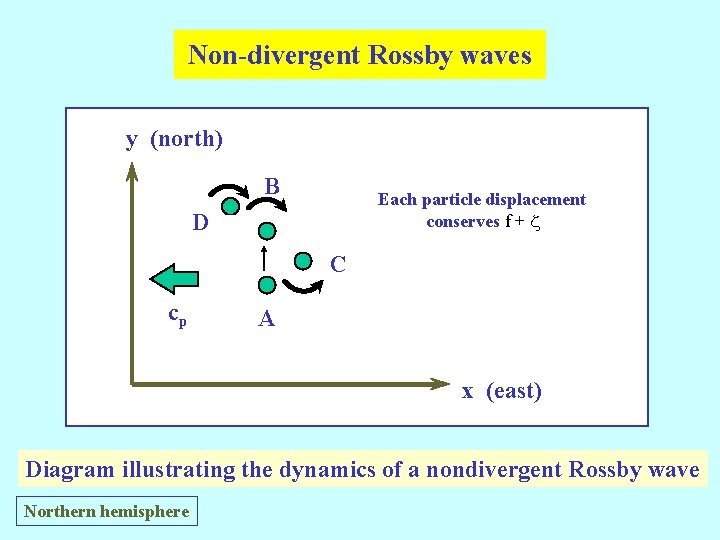
Non-divergent motions Ø A simple description of the basic dynamics of a pure horizontally nondivergent planetary wave may be given by considering two-dimensional flow on a beta plane: Ø i. e. , in a rectangular coordinate system with x pointing eastwards, y pointing northwards, and with f = f 0 + by. Ø Horizontal nondivergence implies that H is a constant and therefore, in the absence of a body force, the vorticity equation reduces to The absolute vorticity of each fluid column remains constant throughout the motion.

Non-divergent Rossby waves y (north) B Each particle displacement conserves f + z D C cp A x (east) Diagram illustrating the dynamics of a nondivergent Rossby wave Northern hemisphere

Mathematical analysis Ø Two-dimensionality implies that there exists a streamfunction y such that a PDE with y as the sole dependent variable. For small amplitude motions, the equation can be linearized For motions independent of y (then u = -yy º there exist travelling wave solutions of the form 0),

where k, w and are constants. Ø k is called the wavenumber and w the frequency Ø The wavelength is l = 2 p/k and the period T = 2 p/w Ø The phase speed of the wave in the x-direction is cp = w/k. Substitution of y into for a nontrivial solution : This is the dispersion relation for the waves.

The phase speed of the wave in the x-direction is: Ø Since cp is a function of k (or l), the waves are called dispersive. Ø In this case, the longer waves travel faster than the shorter waves. Ø Note that b > 0 implies that cp < 0 and hence the waves travel towards the west, consistent with physical arguments. The perturbation northward velocity component is This is exactly 90 deg. out of phase with y.

A basic westerly airflow Ø Suppose now there is a basic westerly airflow (U, 0), U being a constant. Ø Remember westerly means from the west; it is sometimes called a zonal flow. Ø Then u × s linearizes to U¶/¶x and Travelling wave solutions of the type exist as before: The dispersion relation is: w = Uk - b/k

Ø Thus the waves are simply advected with the basic zonal flow. Ø The above equation is known as Rossby's formula. Ø It shows that waves propagate westwards relative to the air at a speed proportional to the square of the wavelength. Ø In particular, waves are stationary when ks = (b/U) Ø They move westwards for l > ls = 2 p/ks and eastwards for l < ls

Planetary waves around the earth Ø If a planetary wave extends around the earth at latitude F, its wavelength cannot exceed the length of that latitude circle, 2 pa cos F , a being the earth's radius. Ø For n waves around the latitude circle at 45° on which b = f/a, then: with corresponding period T = 2 p/|w| = 2 pn/W. Ø Since W = 2 p/(1 day), the period is simply n days.

Ø Values of l, T and cp in the case U = 0 are listed in the table for values of n from 1 to 5. n 1 2 3 4 5 l 103 km 28. 4 14. 2 9. 5 7. 1 5. 7 T days 1 2 3 4 5 cp m s-1 329 82. 2 36. 7 20. 5 13. 5 Ø For n equal to 1 or 2, cp is unrealistically large. => This results from the assumption of nondivergence, which is poor for the ultra-long waves.

Ø The stationary wavelengths ls for various flow speeds U, calculated from the formula are listed below for b as 1. 6 x 10 -11 m -1 s -1, appropriate to 45 deg. latitude. U m s-1 20 40 60 80 l 103 km 7. 0 9. 0 12. 0 14. 0

Planetary waves in the atmosphere Ø Hemispheric upper air charts such as those at 500 mb show patterns with between about 2 and 6 waves. Ø These waves are considered to be essentially planetary waves forced by three principal mechanisms: v orographic forcing resulting from a basic westerly air stream impinging on mountain ranges such as the Rockies and Andes; v thermal forcing due to longitudinal heating differences associated with the distribution of oceans and continents: and v nonlinear interaction with smaller scale disturbances such as extra-tropical cyclones.

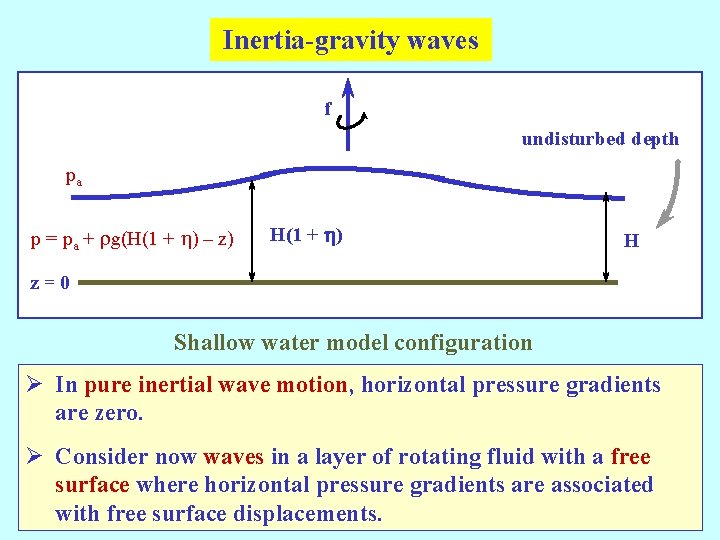
Inertia-gravity waves f undisturbed depth pa p = pa + rg(H(1 + h) – z) H(1 + h) H z=0 Shallow water model configuration Ø In pure inertial wave motion, horizontal pressure gradients are zero. Ø Consider now waves in a layer of rotating fluid with a free surface where horizontal pressure gradients are associated with free surface displacements.

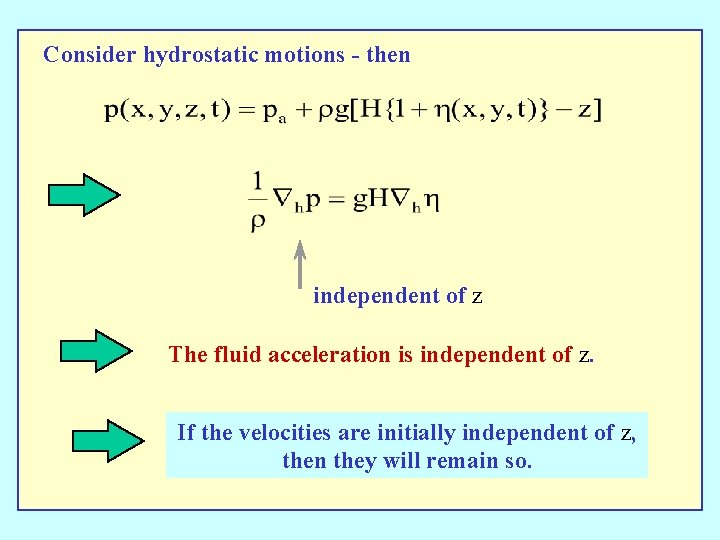
Consider hydrostatic motions - then independent of z The fluid acceleration is independent of z. If the velocities are initially independent of z, then they will remain so.

Linearized equations - no basic flow Consider wave motions which are independent of y. A solution exists of the form if

These algebraic equations for only if have solutions

The solution with w = 0 corresponds with the steady solution (¶/¶t = 0) of the equations and represents a steady current in strict geostrophic balance in which The other two solutions correspond with so-called inertiagravity waves, with the dispersion relation The phase speed of these is The waves are dispersive

Ø The existence of a positive and negative root for w (or cp) shows that these waves can propagate in either x-direction. Ø In the limit as k ® 0, w ® f and the x-dependence of the motion drops out. Ø Then the motion corresponds with the pure inertial wave discussed earlier. Ø In the absence of rotation (i. e. , f = 0) theory reduces to that for small amplitude surface gravity waves on shallow water. Ø Such waves are non-dispersive:

Note that the hydrostatic assumption restricts the validity of the whole analysis to long waves on shallow water; strictly for waves with wavelength l >> H. Rotation is important if => the Rossby radius of deformation for a homogeneous fluid

In the deep ocean, At 45° latitude, f = 10 -4 s-1 and . Rotation effects are important only on the planetary scale.

Inclusion of the beta effect Ø Replace the v-momentum equation by the vorticity equation => where Assume that f can be approximated by its value f 0 at a particular latitude, except when differentiated with respect to y in the vorticity equation. This is justified provided that meridional particle displacements are small.

Ø Again assume that ¶/¶y º wave solutions of the form: 0 and consider travelling- These are consistent only if the determinant is zero

Now expanding by the second row A cubic equation for w with three real roots. When w >> b/k, the two non-zero roots are given approximately by the formula This is precisely the dispersion relation for inertia-gravity waves. When w 2 << g. Hk 2, there is one root given approximately by

Ø For wavelengths small compared with 2 p times the Rossby length reduces to the dispersion relation for nondivergent Rossby waves. For longer wavelengths, the effects of divergence due to variations in the free surface elevation become important, or even dominant.

For extremely long waves These are nondispersive. Ø The importance of divergence effects on the ultra-long waves explains why the calculated phase speeds for planetary waves of global wave-numbers-1 and -2 were unrealistically large. Ø The latter were obtained from the phase speed formula for nondivergent waves. Ø In the atmosphere, divergence effects are not associated with the displacement of a free surface!

Ø To understand the effect of divergence on planetary waves, we introduce the meridional displacement x of a fluid parcel. Ø This is related to the meridional velocity component by v = Dx /Dt, or to a first approximation by Ø Substituting for v in and integrating with respect to time, assuming that all perturbation quantities vanish at t = 0, gives This formula is equivalent (within a linear analysis) to the conservation of potential vorticity (see exercise 11. 2).

In the absence of divergence, holds for a fluid parcel which has x and z initially zero so that z = -bx. The term f 0 h represents the increase in relative vorticity due to the stretching of planetary vorticity associated with horizontal convergence (positive h).

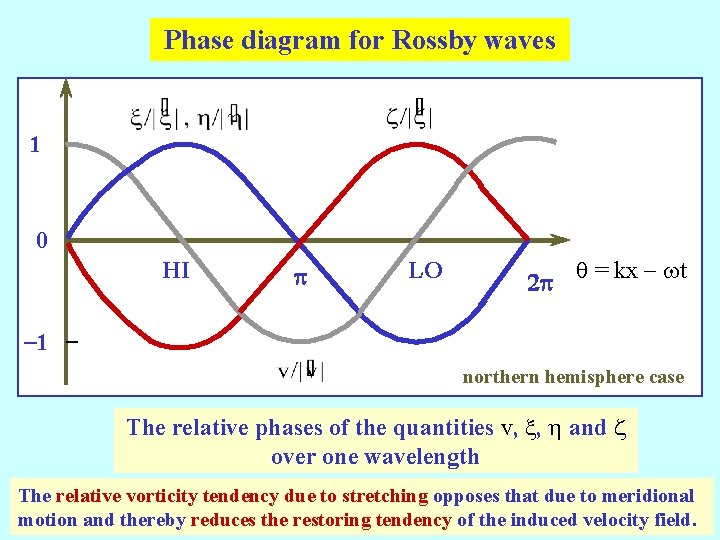
Phase diagram for Rossby waves 1 0 HI p LO 2 p q = kx - wt -1 northern hemisphere case The relative phases of the quantities v, x, h and z over one wavelength The relative vorticity tendency due to stretching opposes that due to meridional motion and thereby reduces the restoring tendency of the induced velocity field.

Filtering Equations: If ¶/¶y º 0 as before, the vorticity equation reduces to an equation for h, and since z = ¶v/¶x => This has the solution , where

Dispersion relation for a divergent planetary wave Ø There is no other solution for w as there was before. Ø In other words, making the geostrophic approximation when calculating v has filtered out in the inertia-gravity wave modes from the equation set, leaving only the low frequency planetary wave mode. Ø This is not too surprising since the inertia-gravity waves, by their very essence, are not geostrophically-balanced motions.

End of Chapter 6