5 1 HOMOGENEOUS PRODUCTION FUNCTION For homogeneous production

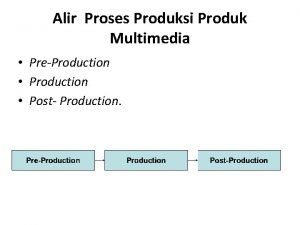
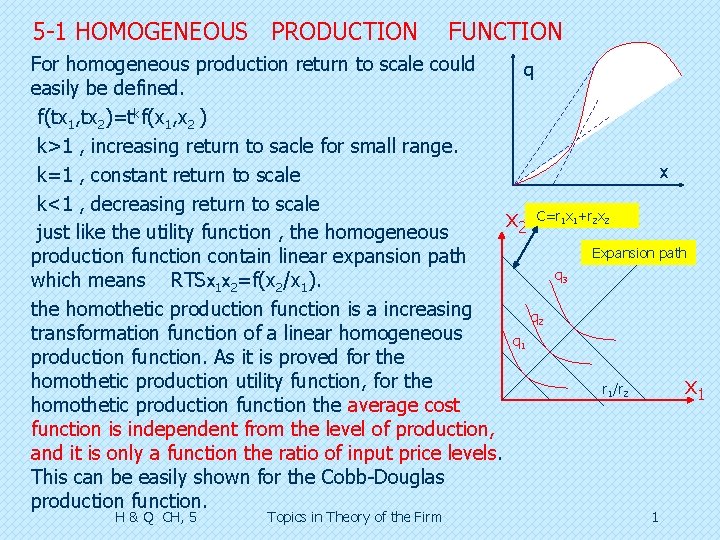
5 -1 HOMOGENEOUS PRODUCTION FUNCTION For homogeneous production return to scale could q easily be defined. f(tx 1, tx 2)=tkf(x 1, x 2 ) k>1 , increasing return to sacle for small range. x k=1 , constant return to scale k<1 , decreasing return to scale x 2 C=r 1 x 1+r 2 x 2 just like the utility function , the homogeneous Expansion path production function contain linear expansion path q 3 which means RTSx 1 x 2=f(x 2/x 1). the homothetic production function is a increasing q 2 transformation function of a linear homogeneous q 1 production function. As it is proved for the homothetic production utility function, for the r 1/r 2 x 1 homothetic production function the average cost function is independent from the level of production, and it is only a function the ratio of input price levels. This can be easily shown for the Cobb-Douglas production function. H & Q CH, 5 Topics in Theory of the Firm 1

5 -1 HOMOGENEOUS PRODUCTION FUNCTION q=f(x 1, x 2) If f(tx 1, tx 2) = tkf(x 1, x 2) , then x 1 f 1 + x 2 f 2 = kf(x 1 , x 2) If k=1 , then x 1 f 1 + x 2 f 2 = q = f(x 1 , x 2) (x 1 f 1)/q + (x 2 f 2)/q = 1 (∂q/ ∂x 1)(x 1/q) + (∂q/ ∂x 2)(x 2/q) =1 єx 1, q + єx 2, q =1 exhaustion theorem , or x 1 f 1 + x 2 f 2 = q marginal productivity theory of distribution two steps ; 1 – each factor should receive its marginal productivity 2 – all output should be exhausted. for k=1, long run profit equals to zero. Π=pq – r 1 x 1 – r 2 x 2 = pq – pf 1 x 1 –pf 2 x 2 = pq –p(f 1 x 1 + f 2 x 2)=pq – pq =0 Π(t)=pf(tx 1, tx 2) – r 1 t x 1 – r 2 t x 2 =t pf(x 1, x 2) –tr 1 x 1 – tr 2 x 2 =tΠ profit function is homogenous of degree one with respect to scale of production. If each factor is paid according to it’s value of marginal product , profit will be zero regardless of its scale of production. H & Q CH, 5 Topics in Theory of the Firm 2

5 -1 HOMOGENEOUS PRODUCTION FUNCTION So when production function is homogeneous of degree one, the scale of production is not defined; If Π>0 , t (scale of production) can be increased forever. If Π<0 the firm will go out of business. If Π=0 scale can not be defined. Solution ; In order to use the exhaustion theorem results, considering the above difficulties; 1 –Production function defined not as homogeneous of degree one. 2 - First and second order condition for profit maximization should exist. 3 - maximum profit should equal to zero. Π=pq – r 1 x 1 – r 2 x 2 =0 , r 1=pf 1 , r 2=pf 2 , Π=pq– pf 1 x 1–pf 2 x 2 =0 , q=f 1 x 1+f 2 x 2 (exhaustion theorem) undefined scale of production, actually means non existence of the second order condition for profit maximization. H & Q CH, 5 Topics in Theory of the Firm 3

5 -1 HOMOGENEOUS PRODUCTION FUNCTION x 1 f 1 + x 2 f 2 =q (f 1+x 1 f 11+x 2 f 21)dx 1 + (f 2 + x 1 f 12 + x 2 f 22 )dx 2 = dq dq/dx 1(dx 2=0)=f 1+f 11 x 1 +x 2 f 21=f 1 , f 11 = (-x 2/x 1)f 21 dq/dx 2(dx 1=0)=f 2+f 22 x 2 +x 1 f 12=f 2 , f 22 = (-x 1/x 2)f 12 f 11 f 22–f 122= f 122 - f 122 = 0(straight line. It should be greater than zero). However, constant return to scale assumption is needed in many cases; what should be done; we assume that 1 -, the whole industry has a constant return to scale production function but the individual firm does not. 2 -Scale of production is finite, in such a way that equates demand with supply in the whole industry. The long run cost function will have a special shape when production function is homogeneous. Suppose that x 10 and x 20 , relates to the one unit of the production level f (tx 10, t x 20)=tk f(x 10, x 20)= tk , so; q = tk c = r 1 x 10 + r 2 x 20 = a → cost of producing one unit H & Q CH, 5 Topics in Theory of the Firm 4

5 -1 HOMOGENEOUS PRODUCTION C=at FUNCTION total cost of producing q units. q=tk production function , C=aq 1/k total cost function , AC = TC/q= aq(1 -k)/k , MC=(a/k)q(1 -k)/k 5 -2 C. E. S. PRODUCTION FUNCTION An special form of homogeneous production function is the one which has Constant Elasticity of Substitution. q=A[αx 1 -ρ + (1 -α)x 2 -ρ ]-1/ ρ homogeneous of degree one. MPx 1=(∂q/∂x 1) =[α/(A-ρ)](q/x 1) ρ+1 homogeneous of degree zero MPx 2=(∂q/∂x 2) =[(1 -α)/(A-ρ)](q/x 2) ρ+1 homogeneous of degree zero RTSx 1 x 2 =( MPx 1)/( MPx 2)=[α/(A-ρ)](q/x 1) ρ+1/[(1 -α)/(A-ρ)](q/x 2) ρ+1 RTSx 1 x 2=[α/(1 -α)](x 2/x 1) ρ+1 , if x 1 increases then RTS wil decrease σ=(f 1 f 2)/(f 12 q) , f 12={(ρ+1) α (1 -α)q 2ρ+1}/A 2ρ , σ=1/(ρ+1) , ρ=(1 - σ)/ σ since σ>0 , then ρ>-1 for concavity condition to prevail. H & Q CH, 5 Topics in Theory of the Firm 5

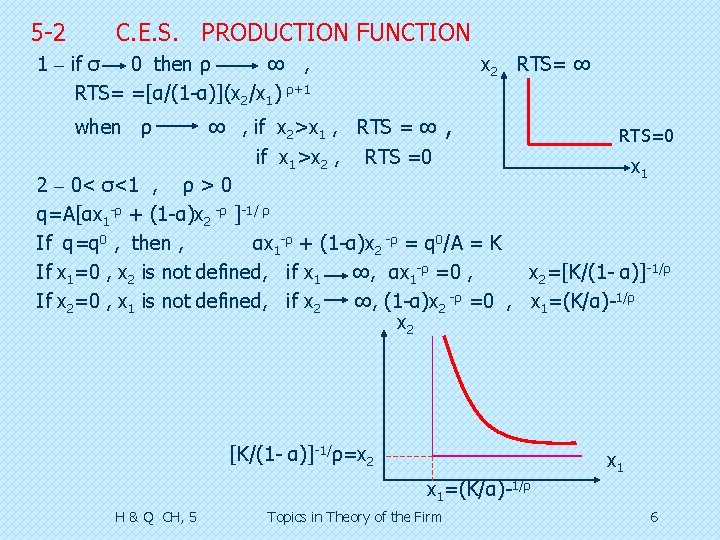
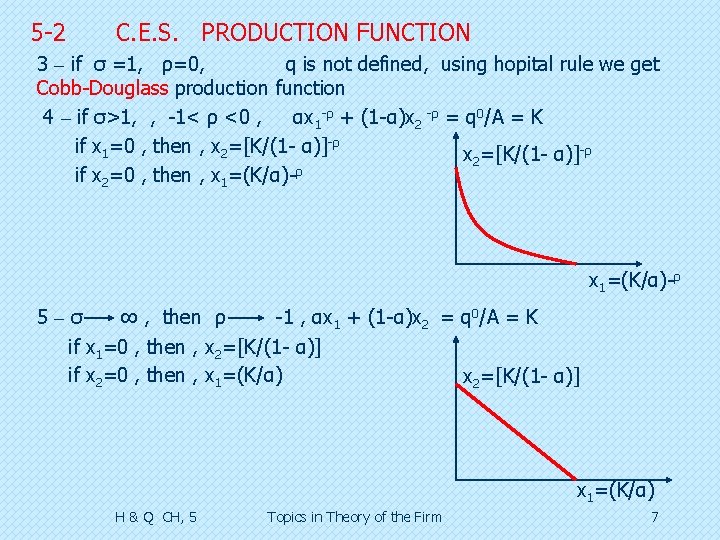
5 -2 C. E. S. PRODUCTION FUNCTION 1 – if σ 0 then ρ ∞ , RTS= =[α/(1 -α)](x 2/x 1) ρ+1 x 2 RTS= ∞ ∞ , if x 2>x 1 , RTS = ∞ , RTS=0 if x 1>x 2 , RTS =0 x 1 2 – 0< σ<1 , ρ > 0 q=A[αx 1 -ρ + (1 -α)x 2 -ρ ]-1/ ρ If q=q 0 , then , αx 1 -ρ + (1 -α)x 2 -ρ = q 0/A = K If x 1=0 , x 2 is not defined, if x 1 ∞, αx 1 -ρ =0 , x 2=[K/(1 - α)]-1/ρ If x 2=0 , x 1 is not defined, if x 2 ∞, (1 -α)x 2 -ρ =0 , x 1=(K/α)-1/ρ x 2 when ρ [K/(1 - α)]-1/ρ=x 2 x 1=(K/α)-1/ρ H & Q CH, 5 Topics in Theory of the Firm 6

5 -2 C. E. S. PRODUCTION FUNCTION 3 – if σ =1, ρ=0, q is not defined, using hopital rule we get Cobb-Douglass production function 4 – if σ>1, , -1< ρ <0 , αx 1 -ρ + (1 -α)x 2 -ρ = q 0/A = K if x 1=0 , then , x 2=[K/(1 - α)]-ρ if x 2=0 , then , x 1=(K/α)-ρ 5–σ ∞ , then ρ -1 , αx 1 + (1 -α)x 2 = q 0/A = K if x 1=0 , then , x 2=[K/(1 - α)] if x 2=0 , then , x 1=(K/α) x 2=[K/(1 - α)] x 1=(K/α) H & Q CH, 5 Topics in Theory of the Firm 7

5 -2 C. E. S. PRODUCTION FUNCTION Estimation of C E S RTSx 1 x 2=[α/(1 -α)](x 2/x 1) ρ+1 =(r 1/r 2) (x 2/x 1) =a(r 1/r 2) σ σ =1/(1+ ρ) log(x 2/x 1)=log a + σ log (r 1/r 2) H & Q CH, 5 Topics in Theory of the Firm a=[(1 -α)/ α] σ 8

5 -3 KHUN-TUCKER CONDITIONS First application; q=f(x 1, x 2) x 1=x 11+x 12 = x 1 bought in the market with the market price equal to r 1 x 11=x 1 produced by the firm with a production function x 11=g(x 3) x 3 = input bought for the production of x 1 with a price equal to r 3 Max Π = pq - TC = pq – (r 1 x 12 + r 2 x 2 +r 3 x 3) S. T. X 11 ≥ g(x 3) Max Π* = pf(x 11+x 12, x 2) – r 1 x 12 – r 2 x 2 – r 3 x 3 +λ[g(x 3) – x 11] ∂Π*/∂x 11 = Π*x 11= pf 1 - λ≤ 0 , x 11 Π*x 11=0 ∂Π*/∂x 12 = Π*x 12= pf 1 – r 1 ≤ 0 , x 12 Π*x 12=0 ∂Π*/∂x 2 = Π*x 2= pf 2 – r 2 ≤ 0 , x 2 Π*x 2=0 ∂Π*/∂x 3 = Π*x 3= λ g’(x 3) – r 3 ≤ 0 , x 3 Π*x 3=0 ∂Π*/∂λ = Π*λ=g(x 3) – x 11 ≥ 0 , λ Π*λ=0 Three cases could be mentioned; H & Q CH, 5 Topics in Theory of the Firm 9

5 -3 KHUN-TUCKER CONDITIONS 1 - x 1 is totally bought from the market; x 11=0 , x 1=x 12 x 11= 0 , Π*x 11 < 0 , pf 1 – λ<0 , pf 1 < λ x 12 ≠ 0 , Π*x 12 = 0 , pf 1 – r 1 = 0 , pf 1 = r 1 x 3=0 , Π*x 3 < 0 , λ g’(x 3) – r 3 <0 , λ < r 3 / g’(x 3) = MCx 1 Pf 1= r 1 < λ < MCx 1 , r 1 < MCx 1 2 – x 1 is totally produced , nothing will be bought from the market. x 11 ≠ 0 , Π*x 11 = 0 , pf 1 – λ=0 , pf 1 = λ x 12 = 0 , Π*x 12 < 0 , pf 1 – r 1 < 0 , pf 1 < r 1 x 3 ≠ 0 , Π*x 3 = 0 , λ g’(x 3) – r 3 =0 , λ= r 3 / g’(x 3) = MCx 1 Pf 1 = λ = MCx 1 , pf 1 < r 1 , , r 1> MCx 1 3 - x 1 is both produced and bought from the market x 11 ≠ 0 , Π*x 11 = 0 , pf 1 – λ=0 , pf 1 = λ x 12 ≠ 0 , Π*x 12 = 0 , pf 1 – r 1 = 0 , pf 1 = r 1 x 3 ≠ 0 , Π*x 3 = 0 , λ g’(x 3) – r 3 =0 , λ= r 3 / g’(x 3) = MCx 1 Pf 1 = λ = MCx 1 , pf 1 = r 1 , , r 1= MCx 1 H & Q CH, 5 Topics in Theory of the Firm 10

5 -3 KHUN-TUCKER CONDITIONS Second application ; q=f(L, K) L=L 1 + L 2 + L 3 If L 1 ≤ L 0 , wage=w If L 2 ≤ 0. 2 L 0 , wage=1. 5 w If L 3 ≤ 0. 2 L 0 , wage=2 w wage discrimination. Max Π 0 = pf(L 1+L 2+L 3, K) - w. L 1 - 1. 5 w. L 2 - 2 w. L 3 – rk + μ 1(L 0 -L 1) + μ 2(0. 2 L 0 -L 2) +μ 3(0. 2 L 0 -L 3) ∂Π 0/∂L 1= Π 0 L 1 = pf. L –w - μ 1 ≤ 0 ∂Π 0/∂L 2= Π 0 L 2 = pf. L – 1. 5 w – μ 2 ≤ 0 ∂Π 0/∂L 3= Π 0 L 3 = pf. L – 2 w – μ 3 ≤ 0 ∂Π 0/∂k = Π 0 k = pfk –r ≤ 0 ∂Π 0/∂ μ 1 = Π 0μ 1 = L 0 –L 1≥ 0 ∂Π 0/∂ μ 2 = Π 0μ 2 = 0. 2 L 0 –L 2≥ 0 ∂Π 0/∂ μ 3 = Π 0μ 3 =0. 2 L 0 –L 3≥ 0 Seven situations is possible; H & Q CH, 5 , , , , L 1 Π 0 L 1=0 L 2 Π 0 L 2=0 L 3 Π 0 L 3=0 k Π 0 k=0 μ 1 Π 0μ 1=0 μ 2 Π 0μ 2=0 μ 3 Π 0μ 3=0 Topics in Theory of the Firm 11

5 -3 KHUN-TUCKER CONDITIONS 1 - L 1= L 2= L 3= 0 L 1= 0 , Π 0 L 1<0 , pf. L- w - μ 1 <0 , L 0 – L 1 >0 , μ 1=0 , pf. L < w 2 - 0< L 1< L 0 , L 2 = L 3 = 0 , L 1> 0 , Π 0 L 1 =0 , pf. L- w - μ 1 =0 , L 0 – L 1 >0 , μ 1=0 , pf. L = w 3 - L 1=L 0 , L 2 = L 3 = 0 , L 1> 0 , Π 0 L 1 =0 , pf. L- w - μ 1 =0 , L 0 – L 1= 0 , μ 1 > 0 , pf. L > w L 2 = 0 , Π 0 L 2 <0 , pf. L- 1. 5 w – μ 2 <0 , 0. 2 L 0 – L 2 >0 , μ 2 =0 pf. L <1. 5 w 4 - L 1=L 0 , 0<L 2<0. 2 L 0 , L 3=0 L 1> 0 , Π 0 L 1 =0 , pf. L- w - μ 1 =0 , L 0 – L 1 = 0 , μ 1 > 0 L 2> 0 , Π 0 L 2 =0 , pf. L- 1. 5 w – μ 2 =0 , 0. 2 L 0 – L 2 >0 , μ 2 =0 H & Q CH, 5 Topics in Theory of the Firm pf. L =1. 5 w 12

5 -3 KHUN-TUCKER 5 - CONDITIONS L 1=L 0 , L 2= 0. 2 L 0 , L 3=0 L 1> 0 , Π 0 L 1 =0 , pf. L- w - μ 1 =0 , L 0 – L 1 = 0 , μ 1 > 0 L 2> 0 , Π 0 L 2 =0 , pf. L- 1. 5 w – μ 2 =0 , 0. 2 L 0 – L 2 =0 , μ 2 >0 6 - L 1=L 0 , L 2= 0. 2 L 0 , 7 - L 1=L 0 , L 2= 0. 2 L 0 H & Q CH, 5 1. 5 w< pf. L<2 w 0< L 3< 0. 2 L 0 pf. L = 2 w L 3 =0. 2 L 0 pf. L > 2 w Topics in Theory of the Firm 13

5 -4 Duality in production Max q=f(x 1, x 2) S. T. C=r 1 x 1+r 2 x 2 cost function could be found from production function Min C=r 1 x 1+r 2 x 2 production function could be found S. T. q 0 =f(x 1, x 2) from cost function (duality ) xi=xi(r 1, r 2, q 0) , or xi=xi(r 1/r 2 , q 0) C=r 1 x 1+r 2 x 2 r 1=λ f 1 , r 2=λ f 2 ( ∂C/∂r 1)=(∂r 1/∂r 1)x 1+ ( ∂x 1/∂r 1)r 1+ ( ∂r 2/∂r 1)x 2 + ( ∂x 2/∂r 1)r 2 =x 1 + λ f 1 ( ∂x 1/∂r 1) + λ f 2 ( ∂x 2/∂r 1)= =x 1 + λ {f 1 ( ∂x 1/∂r 1) + f 2 ( ∂x 2/∂r 1)}=x 1+ λ{∂q 0/∂r 1}=x 1 { ∂C(q, r 1, r 2)/∂r 1 }=x 1(q , r 1, r 2) { ∂C(q, r 1, r 2)/∂r 2 }=x 2(q , r 1, r 2) From the above equations we could find q in terms of x 1 and x 2 H & Q CH, 5 Topics in Theory of the Firm 14

5 -4 Duality in production Example ; C=A(r 1 ar 2 b)1/(a+b)q 1/(a+b) A=(a+b)(aabb)-1/(a+b) ∂C/∂r 1= {a/(a+b)}Aq 1/(a+b)(r 2/r 1)b/(a+b)= x 1 ∂C/∂r 2= {b/(a+b)}Aq 1/(a+b)(r 2/r 1)-a/(a+b)= x 2 x 1 ax 2 b = q {[a/(a+b)]a[b/(a+b)]b A(a+b)} q = x 1 ax 2 b [ 1/{[a/(a+b)]a[b/(a+b)]b A(a+b)}]= B x 1 ax 2 b H & Q CH, 5 Topics in Theory of the Firm 15

5 -5 PRODUCTION UNDER UNCERTAINTY Basic idea; Under certainty people know exactly what they are getting and how much utility they will yield. There are three types of uncertainty; 1 - some goods by their nature are games. like ; horse riding bets or insurance or stock market transaction. In these cases purchase does not guarantee a particular outcome. 2 - Dealing with others, or uncertainty about the action of individuals. 3 - Lack of understanding of information. Like information about weather condition. For this reason people are willing to pay for these kind of information. We only concentrate on the first type of uncertainty. Game x ; prizes of x 1 , x 2 , x 3 , …. . xn probability v 1 , v 2 , v 3 , …. . vn H & Q CH, 5 Topics in Theory of the Firm 16

5 -5 PRODUCTION UNDER UNCERTAINTY Game ; Flipping a coin x 1 =win $1( Head) , x 2=loose $1(Tail) E(x) = v 1 x 1 + v 2 x 2 =(1/2)(+1) + (1/2)( -1) = 0 If the player plays the game many times (n ∞) he will neither loose nor win. Game ; Flipping a coin x 1 =win $4( Head) , x 2=loose $3(Tail) E(x) = v 1 x 1 + v 2 x 2 =(1/2)(+4) + (1/2)( -3) = 1/2 If the player plays the game many times (n ∞) he will win $ 1/2. FAIR GAMES; If cost of entry is equal to the expected value of the game, the game is called fair game. We expect that people accept the fair games. But , the Petersburg paradox showed that this is not the case. . H & Q CH, 5 Topics in Theory of the Firm 17

5 -5 PRODUCTION UNDER UNCERTAINTY Petersburg paradox ; Game ; Flipping a coin till head appears Xi= represent the prize awarded when the head appears. The game could be played infinitely. amount of win probability of win x 1=$2 v 1=1/2 x 2=$22 v 2 =(1/22) x 3=$23 v 3=(1/23) …. . ………. xn=$2 n vn=(1/2 n) n ∞ E(x)=Σ vi xi = ( 1+1+1+…. . +1)= ∞ Is there any one who is willing to pay infinite amount of money for this game? Bernolli tried to solve the puzzle, by introducing the concept of Utility. He said that the utility of the win is important for decision making rather the amount of the win by itself. H & Q CH, 5 Topics in Theory of the Firm 18

5 -5 PRODUCTION UNDER UNCERTAINTY U(x)=alog(xi)=utility of the amount of win (x) u(x 1)=$alog 2 u(x 2)=$alog 22 u( x 3)=$alog 23 …. . u(xn)=$alog 2 n probability of win v 1=1/2 v 2 =(1/22) v 3=(1/23) ………. vn=(1/2 n) n ∞ E[u(x)]=Σviu(xi)=(1/2)alog 2+(1/22) alog 22 +……. . +(1/2 n) alog 2 n =alog 2Σ(i/2 i )=2 alog 2 As it is seen the expected utility of x is defined , but there is no upper bond on u(x). “a” could be very large, and the expected utility could be defined very large and unreasonable. Another attempt is made by J. V. Neuman, and O. Morgenstern by introducing the concept of decision theory under the uncertain situations, situations an attempt by these two to generalize some of the foundations of theory of individual choice to cover uncertain situation. H & Q CH, 5 Topics in Theory of the Firm 19

5 -5 PRODUCTION UNDER UNCERTAINTY Utility index The first attempt to in explaining theory is to assign indices to utility under uncertain situations. Prizes ; x 1, x 2, x 3 , …. xn xn is the most preferred Prob. v 1 , v 2 , ……. vn U(x 1) = 0 ; U(xn ) = 1 J. V. Neuman, and O. Morgenstern showed that there is a reasonable way to assign specific utility numbers to the different prizes available. What they proved is that a probability like Πi exist which makes the following relation holds; U(xi) = Πi u(xn)+(1 - Πi) u(x 1) What this relation means is that, that there exist a probability such as Πi which makes the individual indifferent between the following two alternatives, (or both alternatives have the same satisfaction for the individual); 1 - having xi with certainty, (with a satisfaction of u(xi)) and 2 -a game winning xn with probability Πi and winning x 1 with probability (1 - Πi), {with a satisfaction of [Πi u(xn)+(1 - Πi) u(x 1)]} H & Q CH, 5 Topics in Theory of the Firm 20

5 -5 PRODUCTION UNDER UNCERTAINTY Suppose that we assign two numbers to u(xn) and u(x 1) U(xn) = 1 , and U(x 1) = 0 U(xi) = Πi u(xn)+(1 - Πi) u(x 1) = Πi for each i =1, 2, …. n , there exist a probability like Πi which is equal to the utility of having xi with certainty. So these probabilities could be considered as utility indices. Expected utility maximization; Using the utility index it is possible to prove that a rational individual will choose among the uncertain situations based upon their expected value of utility to him. The one with the highest expected utility will be chosen. Suppose that individual faces two games; Game 1 ; winning x 2 with probability (q) , winning x 3 with probability (1 -q), Game 2 ; winning x 5 with probability (t), winning x 6 with probability (1 -t) H & Q CH, 5 Topics in Theory of the Firm 21

5 -5 PRODUCTION UNDER UNCERTAINTY E[u(1)]=q u(x 2)+(1 -q) u(x 3)=q Π 2+(1 -q) Π 3 E[u(1)]=q[Π 2 u(xn)+(1 - Π 2) u(x 1)]+(1 -q) [Π 3 u(xn)+(1 - Π 3) u(x 1)] E[u(1)]=[q Π 2+(1 -q) Π 3] u(xn)+[q (1 - Π 2) + (1 -q) (1 - Π 3)] u(x 1) If Πa=[q Π 2+(1 -q) Π 3], then [q (1 - Π 2) + (1 -q) (1 - Π 3)]=(1 - Πa) E[u(1)]= Πau(xn) +(1 - Πa)u(x 1)= Πa E[u(2)]=t u(x 5)+(1 -t) u(x 6)=t Π 5+(1 -t) Π 6 E[u(2)]=t [Π 5 u(xn)+(1 - Π 5) u(x 1)]+(1 -t) [Π 6 u(xn)+(1 - Π 6) u(x 1)] E[u(2)]=[tΠ 5+(1 -t) Π 6] u(xn)+[t (1 - Π 5) + (1 -t) (1 - Π 6)] u(x 1) If Πb =[t Π 5 +(1 -t) Π 6], then [t (1 - Π 5) + (1 -t) (1 - Π 6)]=(1 - Πb) E[u(2)]= Πb u(xn) +(1 - Πb )u(x 1)= Πb If E[u(1)]> E[u(2)] , then ; Πa>Πb Game one will be chosen because it yields a higher utility. H & Q CH, 5 Topics in Theory of the Firm 22

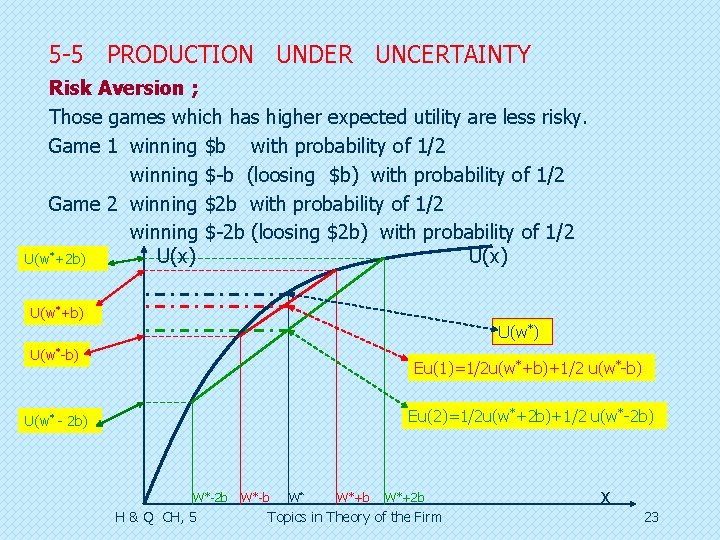
5 -5 PRODUCTION UNDER UNCERTAINTY Risk Aversion ; Those games which has higher expected utility are less risky. Game 1 winning $b with probability of 1/2 winning $-b (loosing $b) with probability of 1/2 Game 2 winning $2 b with probability of 1/2 winning $-2 b (loosing $2 b) with probability of 1/2 U(x) U(w*+2 b) U(w*+b) U(w*-b) Eu(1)=1/2 u(w*+b)+1/2 u(w*-b) Eu(2)=1/2 u(w*+2 b)+1/2 u(w*-2 b) U(w* - 2 b) W*-2 b H & Q CH, 5 W*-b W* W*+b W*+2 b Topics in Theory of the Firm x 23

5 -5 PRODUCTION UNDER UNCERTAINTY An individual who always rejects fair bets is said to be risk-averse. His marginal utility of income(wealth) is decreasing. He will always willing to pay a premium to insure himself against the risk. Change uncertain position to certain one. Production behavior ; There are two source of uncertainty for a producer; price and quantity. At the first stage, suppose that price is not certain: p 1 , p 2 , p 3 , …. . pn price level v 1 , v 2 , v 3 , …. . vn probability Πi=piq – c(q) profit level when price =pi u(Πi) utility obtained from the profit level when price is p i E[u(Π)]=Σin [vi u(Πi)]= expected utility of profit derived in the uncertain situation. In the uncertain situations the producer should maximize the expected utility of profit, rather than maximizing the expected level of profits. d Σin [vi u(Πi)]/dq = 0 , Σin vi u’(Πi)(pi – c’(q))=0 H & Q CH, 5 Topics in Theory of the Firm 24

5 -5 PRODUCTION UNDER UNCERTAINTY There could be three situations; 1 - individual is risk netural. He is indifferent between risky and non risky situations. d u’(Πi)/dΠi = 0 , u’(Πi)=A is constant, u”(Πi)=0 v 1 A(p 1 – c’(q))+ v 2 A(p 2 – c’(q))+…. vn A(pn – c’(q)=0 , q=q 0 2 - individual is risk averse. He prefers non risky situation to risky situation. d u’(Πi)/dΠi < 0 , u’(Πi)=is decreasing , u”(Πi) < 0 v 1 u’(Π 1)(p 1–c’(q))+ v 2 u’(Π 2)( (p 2–c’(q))+…. vn u’(Πn)(pn–c’(q))=0, , q=q 1 and u’(Π 1)> u’(Π 2)>……. u’(Πn), q 1<q 0 3 - individual is risk taker. He is prefers risky situation to non risky situation. d u’(Πi)/dΠi > 0 , u’(Πi)=is increasing , u”(Πi) > 0 v 1 u’(Π 1)(p 1–c’(q))+ v 2 u’(Π 2)( (p 2–c’(q))+…. vn u’(Πn)(pn–c’(q))=0 q=q 2 q 2>q 0 , and u’(Π 1)< u’(Π 2)<……. u’(Πn), H & Q CH, 5 Topics in Theory of the Firm 25

5 -5 PRODUCTION UNDER UNCERTAINTY 2 - suppose that price is known but quantity is not known. (future market in the agricultural products). quantity q 1 , q 2 , q 3 , …. qn target = q 0, qi=φiq 0 φi= percent of q 0 which depends on climate. probability ; v 1 , v 2 , v 3 , …. vn Πi=pφiq 0 – c(q 0) Producer decision is to find the target production level d Σin [vi u(Πi)]/dq = 0 , Σin vi u’(Πi)(p φi – c’(q))=0 the same result will be obtained. H & Q CH, 5 Topics in Theory of the Firm 26

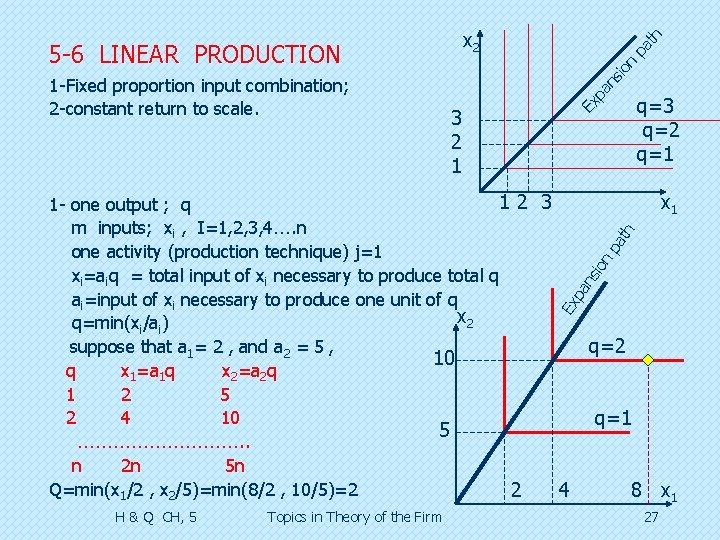
ns pa q=3 q=2 q=1 Ex pa th x 1 Ex pa n 12 3 1 - one output ; q m inputs; xi , I=1, 2, 3, 4…. n one activity (production technique) j=1 xi=aiq = total input of xi necessary to produce total q ai=input of xi necessary to produce one unit of q x 2 q=min(xi/ai) suppose that a 1= 2 , and a 2 = 5 , 10 q x 1=a 1 q x 2=a 2 q 1 2 5 2 4 10 5 ……………. . n 2 n 5 n Q=min(x 1/2 , x 2/5)=min(8/2 , 10/5)=2 2 4 n 3 2 1 sio 1 -Fixed proportion input combination; 2 -constant return to scale. io n 5 -6 LINEAR PRODUCTION pa th x 2 H & Q CH, 5 Topics in Theory of the Firm q=2 q=1 8 x 1 27

5 -6 LINEAR PRODUCTION 2 - one output q m input xi i = 1, 2, …. m n activity j=1, 2, ……. n q = Σ 1 n qj xi= Σj=1 n aij qj aij = xi necessary to produce one unit of q in the jth activity. input of xi necessary to produce one unit of q = Ai Ai = (xi/q)=Σj=1 n aij (qj/q) = Σj=1 n aij λj λj= qj/q q=min(xi/Ai) Suppose that there are three activities and two inputs; j=1 J=2 X 1 a 11=1 a 12 =2 a 13=4 X 2 a 21=8 a 22=5 a 23=3 input activity H & Q CH, 5 Topics in Theory of the Firm J=3 28

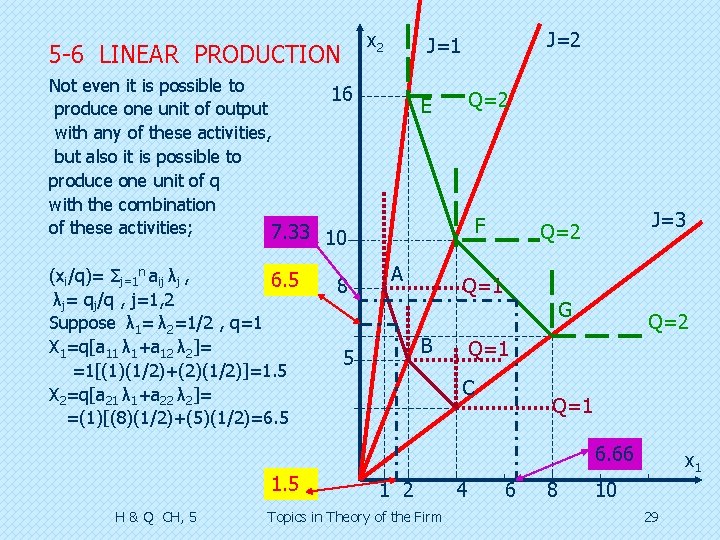
x 2 5 -6 LINEAR PRODUCTION Not even it is possible to produce one unit of output with any of these activities, but also it is possible to produce one unit of q with the combination of these activities; 7. 33 (xi/q)= Σj=1 n aij λj , 6. 5 λj= qj/q , j=1, 2 Suppose λ 1= λ 2=1/2 , q=1 X 1=q[a 11 λ 1+a 12 λ 2]= =1[(1)(1/2)+(2)(1/2)]=1. 5 X 2=q[a 21 λ 1+a 22 λ 2]= =(1)[(8)(1/2)+(5)(1/2)=6. 5 J=2 J=1 16 Q=2 E F 10 8 A Q=1 B 5 J=3 Q=2 G Q=2 Q=1 C Q=1 6. 66 1. 5 H & Q CH, 5 1 2 Topics in Theory of the Firm 4 6 8 x 1 10 29

5 -6 LINEAR PRODUCTION Suppose λ 2=1/3 λ 3=2/3 , q=2 X 1=q[a 12 λ 2+a 13 λ 3]= =2[(2)(1/3)+(4)(2/3)]=6. 66 X 2=q[a 22 λ 2 + a 23 λ 3]= =(2)[(5)(1/3)+(3)(2/3)=7. 33 Only points on ABC line or EFG line are efficient. Any other point is not efficient. Efficient point , (comparing to any other point), is the one that can produce the same level of output with minimum amount of inputs. In the same manner ith activity is not efficient if another activity like j, could be found which produce the same output with less output (either x 1 or x 2 or both should be lower). 3 - s outputs qh h=1, 2, 3, 4…. . s m inputs xi i = 1, 2, 3, 4…. one activity xi = Σh=1 s aihqh aih = input xi necessary to produce one unit of output h. H & Q CH, 5 Topics in Theory of the Firm 30

5 -6 LINEAR PRODUCTION 4 - h outputs qh h=1, 2, 3, 4, …. . s m inputs xi i =1, 2, 3……. m n activity j=1, 2, 3……. N qh= Σj=1 n ahj zj xi = Σj=1 n bij zj ahj=amount of output h in one unit of composite commodity basket in activity j. composite commodity basket = basket of commodities contains from h outputs. Zj= units of composite commodities produced in activity j bij= input i used for the production of one unit of composite commodity in activity j. H & Q CH, 5 Topics in Theory of the Firm 31

5 -6 LINEAR PRODUCTION Application of linear programming for linear activities; Max TR=p 1 q 1 + p 2 q 2 +…… pnqn original S. T. ai 1 q 1 + ai 2 q 2 +……. . ainqn ≤ xi 0 i = 1, 2, 3 , …. m L= p 1 q 1+ p 2 q 2 +……. + λ 1 [x 10 – (a 11 q 1+a 12 q 2+……a 1 nqn)] + λ 2 [x 20 – (a 21 q 1+a 22 q 2+……a 2 nqn)] …………………… + λm [xm 0 – (am 1 q 1+am 2 q 2+……amnqn)] (∂L/∂q 1)=Lq 1= p 1 - λ 1 a 11 – λ 2 a 21 - ……- λmam 1≤ 0 , q 1 Lq 1=0 (∂L/∂q 2)=Lq 2= p 2 - λ 1 a 12 – λ 2 a 22 - ……- λmam 2≤ 0 , q 2 Lq 2=0 …………………………………. . (∂L/∂qn)=Lqn= pn - λ 1 a 1 n – λ 2 a 2 n - ……. λmamn≤ 0 , qn Lqn=0 (∂L/∂λ 1)= Lλ 1 = x 10 – a 11 q 1 –a 12 q 2 -…………- a 1 nqn ≥ 0 , λ 1 Lλ 1 = 0 (∂L/∂λ 2)= Lλ 2 = x 20 – a 21 q 1 –a 22 q 2 -…………- a 2 nqn ≥ 0 , λ 2 Lλ 2 = 0 …………………………………… (∂L/∂λm)= Lλm = xm 0 – am 1 q 1 –am 2 q 2 -…………- amnqn ≥ 0 , λm Lλm = 0 m+n equations, m+n unkowns (λ 1…. λm, q 1, …qn) Max TR* = Σj=1 n pjqj* H & Q CH, 5 Topics in Theory of the Firm 32

5 -6 LINEAR PRODUCTION Min TC=r 1 x 1+r 2 x 2+…. . +rmxm dual S. T. a 1 jr 1+a 2 jr 2+………. . amjrm≥ pj j=1, 2, 3……. n. aijr 1+a 2 jr 2+………. . amjrm= average cost of qj In the long run equilibrium in perfect competition , average cost could not be lower than price. If Acqj is lower than price, the optimum solution (minimum cost) for ri will be ri = 0. L=r 1 x 1+r 2 x 2+……+rmxm+ μ 1[p 10 – (a 11 r 1+a 21 r 2+……. +am 1 rm)] ……………………. +μn[pn 0 – (a 1 n r 1+a 2 n r 2+……. +amn rm)] (∂L/∂r 1)=Lr 1=x 1 - μ 1 a 11 - …. - μna 1 n ≥ 0 , r 1 Lr 1=0 (∂L/∂r 2)=Lr 2=x 2 - μ 1 a 21 - …. - μna 2 n ≥ 0 , r 2 Lr 2=0 …………………………. . (∂L/∂rm)=Lrm=xm- μ 1 am 1 - …. - μnamn ≥ 0 , rm. Lrm=0 (∂L/∂μ 1)=Lμ 1=p 1 - a 11 r 1 - …. - am 1 rm ≤ 0 , μ 1 Lμ 1=0 (∂L/∂μ 1)=Lμ 2=p 2 - a 12 r 1 - …. - am 2 rm ≤ 0 , μn. Lμn=0 ……………………………… (∂L/∂μn)=Lμn=pn - a 1 n r 1 - …. -amn rm ≤ 0 , μn. Lμn=0 m+n equations, m+n unknown , (r 1 …rm , μ 1…μn) H & Q CH, 5 Topics in Theory of the Firm 33

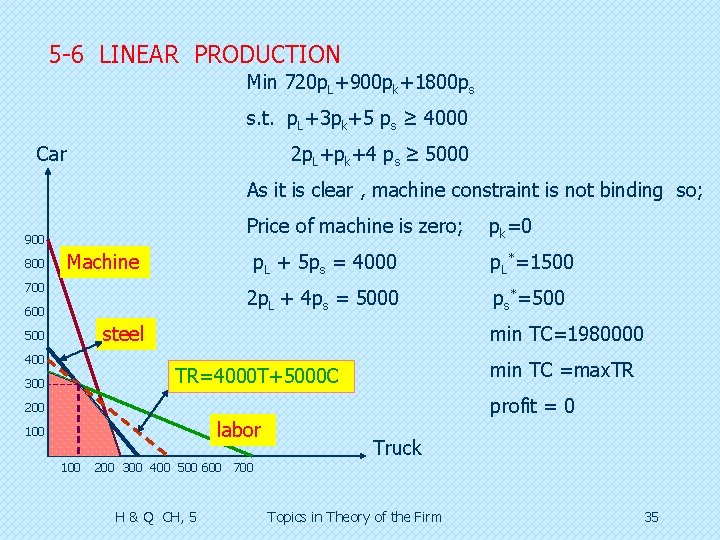
5 -6 LINEAR PRODUCTION Comparing original and dual F. O. C. Original parameter=dual constraint = pj Original constraint = dual parameter=xi ri* =λi* = shadow price of xi ; TC*=Σimri*xi=Σjn pjqj*=TR* qj*=μj*= shadow quantity for qj ; TC*=Σimri*xi=Σjn pjqj*=TR* Example ; production of Car and Truck, price of car=5000 , price of truck=4000 Resource Labor Machine Steel Total available 720 L. H. 900 M. H. 1800 T Max TR=4000 T + 5000 C S. T. T + 2 C ≤ 720 3 T + C ≤ 900 5 T +4 C ≤ 1800 H & Q CH, 5 required to produce one unit Truck 1 L. H. 3 M. H. 5 Ton required to produce one unit of Car 2 L. H. 1 M. H. 4 Ton C*=300 , T* =120 max TR=1980000 Topics in Theory of the Firm 34

5 -6 LINEAR PRODUCTION Min 720 p. L+900 pk+1800 ps s. t. p. L+3 pk+5 ps ≥ 4000 Car 2 p. L+pk+4 ps ≥ 5000 As it is clear , machine constraint is not binding so; Price of machine is zero; 900 800 p. L + 5 ps = 4000 p. L*=1500 2 p. L + 4 ps = 5000 ps*=500 Machine 700 600 min TC=1980000 steel 500 400 min TC =max. TR TR=4000 T+5000 C 300 profit = 0 200 labor 100 pk=0 200 300 400 500 600 700 H & Q CH, 5 Truck Topics in Theory of the Firm 35

H & Q , CH 5 , PROBLEMS; Q 5 -1 ; Each of the following production functions is homogeneous of degree one. In each case, derive the marginal products for x 1 and x 2 and demonstrate that they are homogenous of degree zero: (a) : q=(ax 1 x 2 – bx 12 - cx 22 )/(ax 1+bx 2) (b) : q=Ax 1 ax 21 -a + bx 1+ cx 2 solution; a ; (dq/dx 1)= [(ax 1 -2 bx 1)(ax 1+bx 2)-a(ax 1 x 2 – bx 12 - cx 22 )]/(ax 1+bx 2)2 MPx 1(mx 1, mx 2)= m 2 [(ax 1 -2 bx 1)(ax 1+bx 2)-a(ax 1 x 2 – bx 12 - cx 22)/m 2(ax 1+bx 2)2= MPx 1(x 1, x 2) (dq/dx 2)= [(ax 2 – 2 cx 2)(ax 1+bx 2)-a(ax 1 x 2 – bx 12 - cx 22 )]/(ax 1+bx 2)2 MPx 2(mx 1, mx 2)= m 2 [(ax 2 -2 cx 2)(ax 1+bx 2)-a(ax 1 x 2 – bx 12 - cx 22 ]/m 2(ax 1+bx 2)2= MPx 1(x 1, x 2) B; (dq/dx 1)=a. Ax 1 a-1 x 21 -a +b=a. A(x 1/x 2)a-1, (dq/dx 2)=a. Ax 1 ax 2 -a +b=a. A(x 1/x 2)a, H & Q CH, 5 Topics in Theory of the Firm MP(mx 1, mx 2)=MP(x 1, x 2) 36

H & Q , CH 5 , PROBLEMS; Q 5 -2 ; An entrepreneur uses two distinct production processes to produce two distinct goods, Q 1 and Q 2. The production function for each good is CES, and the entrepreneur obeys the equilibrium condition for each. Assume that Q 1 has a higher elasticity of substitution and a lower value for the parameter than Q 2. Determine the input price ratio at which the input use ratio would be the same for both goods. Which good would have the higher input use ratio if the input price ratio were lower? Which would have the higher use ratio if the price ratio were higher? Solution; the equilibrium conditions are as follows; k 1=a 1 rσ1 k 2=a 2 rσ2 ki=input use ratio for i = (x 1/x 2)i by assumption; σ1> σ2 and a 1 > a 2. if k 1=k 2 , then a 1 rσ1 = a 2 rσ2 , so ; r = (a 2/a 1) =r* by assumption ; (σ1 - σ2)>0 , if r=r* , then k 1=k 2 , and if r> r* , then k 1>k 2 and vice versa H & Q CH, 5 Topics in Theory of the Firm 37

H & Q , CH 5 , PROBLEMS; Q 5 -3 ; An entrepreneur has the production function of the form q=Ax 1 ax 21 -a. She buys input and sells output at fixed prices, but is subject to a quota which allows her to purchase not more than x 10 units of x 1. She would have purchased more in the absence of quota. Use the Kuhn-Tucker analysis to determine the entrepreneur’s conditions for profit maximization. What is the optimal relation between the value of the marginal product of each input and its price. What is the optimal relation between the RTS and the input price ratio. Solution; Max Π = pq – r 1 x 1 – r 2 x 2 + λ(x 10 -x 1) (∂Π/∂x 1)= p. MPx 1 – r 1 - λ ≤ 0 , (∂Π/∂x 1)x 1= 0 (∂Π/∂x 2)= p. MPx 2 – r 2 ≤ 0, (∂Π/∂x 2)x 2= 0 (∂Π/∂ λ)= (x 10 -x 1) ≥ 0 , λ(x 10 -x 1) =0 if x 1=0, p. MPx 1< r 1+ λ and if x 1>0, p. MPx 1 = r 1+ λ if x 2=0, p. MPx 2< r 2 and if x 2>0, p. MPx 2 = r 2=p. MPx 2=p(1 -a)A(x 1/x 2)a r 1=p. MPx 1=pa. A(x 1/x 2)a-1 - λ RTS = (MPx 1/MPx 2)=(r 1+ λ)/r 2 > r 1 /r 2 H & Q CH, 5 Topics in Theory of the Firm 38

H & Q , CH 5 , PROBLEMS; Q 5 -4 ; Use Shepherd's lemma to find the production function that corresponds to the cost function C=(r 1+2(r 1 r 2)1/2 +r 2)q and demonstrate that it is CES. Solution ; (∂C/∂r 1)=(1+r 2(r 1 r 2)-1/2 )q (∂C/∂r 2)=(1+r 1(r 1 r 2)-1/2 )q if r=(r 1/r 2) (∂C/∂r 1)=(1+r 2(r 1 r 2)-1/2 )q=(1+ r– 1/2)q (∂C/∂r 2)=(1+r 1(r 1 r 2)-1/2 )q=(1+ r 1/2)q (1+ r– 1/2)q = x 1 (1+ r 1/2) q =x 2 q=x 1 x 2/ (x 1+x 2) = ½[(1/2)x 1 -1+ (1/2)x 2 – 1]-1 Q 5 -5 ; A farmer who sells at a fix price of 5 dollars per unit and has the cost function C=3. 5+0. 5 q 2 , plans to maximizes profit under certainty. After planning she discovers that she can have a fertilizer applied that will increase her yield 40 percent with a probability of 0. 25 percent, 60 percent with a probability of 0. 5 , and 88 percent with a probability of 0. 25. Her utility function is U=(Π)1/2. Determine the maximum amount that she is willing to pay for the fertilizer application. Contrast this amount with the expected value of the increase in her profit as a result of fertilizer application. H & Q CH, 5 Topics in Theory of the Firm 39

H & Q , CH 5 , PROBLEMS; Solution ; q=target , P=5 , C(q)=3. 5 + 0. 5 q 2 , U=Π 1/2 , U’=(1/2) Π-1/2 (v 1=1/4 , δ 1=1. 4) , (v 2=1/2 , δ 2=1. 6) , (v 3=1/4 , δ 3=1. 88) EU(Π)=Σi 3 vi u[( Πi )] = Σi 3 vi u[ pδiq – C(q)] , Πi = pδiq – C(q) d[EU(Π)]/dq = Σi 3 vi u’ (Πi)[ pδi – C’ (q)]= 0 q=q 0 , EU(Π)= Σi 3 vi u[ pδiq 0 – C(q 0)] =U 0 no fertilizer situation; p=mc , q=5 , Π = pq – TC = 25 – (3. 5 +(0. 5)(25) ) = 9 u =(Π)1/2 =3 U 0 should be greater than 3 for the farmer to use fertilizer. The difference between these two (U 0 – 3) is the farmer’s gain in terms of utility and maximum amount that he is willing to pay for fertilizer. d( E(Π))/dq =d{v 1 Π 1 + v 2 Π 2 + v 3 Π 3=1/4[(5)(1. 4 q) - 3. 5 – 0. 5 q 2 ] +1/2[(5)(1. 6 q) - 3. 5 – 0. 5 q 2 ] + 1/4[(5)(1. 88 q) - 3. 5 – 0. 5 q 2 ]]/dq = 0 q=A , → E(Π) = Π* , U* = U(Π*) , U* can be compared with U 0 H & Q CH, 5 Topics in Theory of the Firm 40

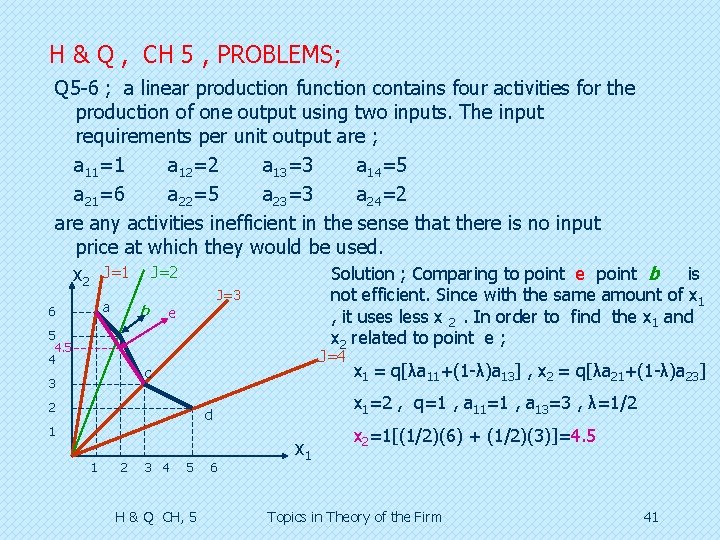
H & Q , CH 5 , PROBLEMS; Q 5 -6 ; a linear production function contains four activities for the production of one output using two inputs. The input requirements per unit output are ; a 11=1 a 12=2 a 13=3 a 14=5 a 21=6 a 22=5 a 23=3 a 24=2 are any activities inefficient in the sense that there is no input price at which they would be used. Solution ; Comparing to point e point b x 2 J=1 J=2 a 6 b 5 4 is not efficient. Since with the same amount of x 1 , it uses less x 2. In order to find the x 1 and x 2 related to point e ; J=3 e J=4 c 3 2 x 1=2 , q=1 , a 11=1 , a 13=3 , λ=1/2 d 1 1 2 3 4 5 H & Q CH, 5 6 x 1 = q[λa 11+(1 -λ)a 13] , x 2 = q[λa 21+(1 -λ)a 23] x 1 x 2=1[(1/2)(6) + (1/2)(3)]=4. 5 Topics in Theory of the Firm 41

H & Q , CH 5 , PROBLEMS; Q 5 -7 Each of the linear activities yields s outputs and uses m inputs as described by h outputs qh h=1, 2, 3, 4, …. . s m inputs xi i =1, 2, 3……. m n activity j=1, 2, 3……. N qh= Σj=1 n ahj zj xi = Σj=1 n bij zj ahj= the amount of output h in one unit of composite commodity in activity j. composite commodity = basket of commodities contains from h outputs. Zj= units of composite commodities produced in activity j bij= input i used for the production of one unit of composite commodity in activity j. An entrepreneur possesses fixed quantities of each of the inputs. She desires to maximizes her total revenue from the sale of outputs at constant market prices. Formulate her optimization problem as a linear-programming system, and derive the dual programming system. H & Q CH, 5 Topics in Theory of the Firm 42

H & Q , CH 5 , PROBLEMS; Solution ; If ph is the price of qh , total income is equal to Y ; ahj=amount of output h in one unit of composite commodity in activity j. composite commodity = basket of commodities contains from h outputs. Zj= units of composite commodities produced in activity j bij= input i used for the production of one unit of composite commodity in activity j Y = Σhs ph qh = Σhs ph Σj=1 n ahj zj , so maximization problem is ; max Y = Σhs ph Σj=1 n ahj zj total revenue S. T. xi = Σj=1 n bij zj =input constraint (decision variable = Zj). the dual formulation is; Min C=Σim ri xi total cost S. T. Σim bij ri ≥ yj (yj = Σhs ph ahj =revenue from one level of Zj , Zj =1 ) Σim bij ri=cost of producing one level of Zj (decision variable=ri) Σim bij ri = cost of production of one unit of composite commodity in activity j. yj= ph Σj=1 n ahj = Σj=1 n ph ahj = income received from the sale of one unit of composite commodity in activity j. H & Q CH, 5 Topics in Theory of the Firm 43