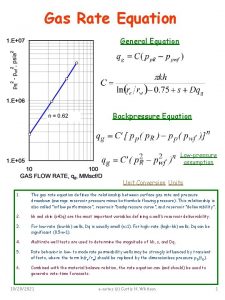
TOPIC INTEGRAL EQUATION Definition Integral equation An integral


























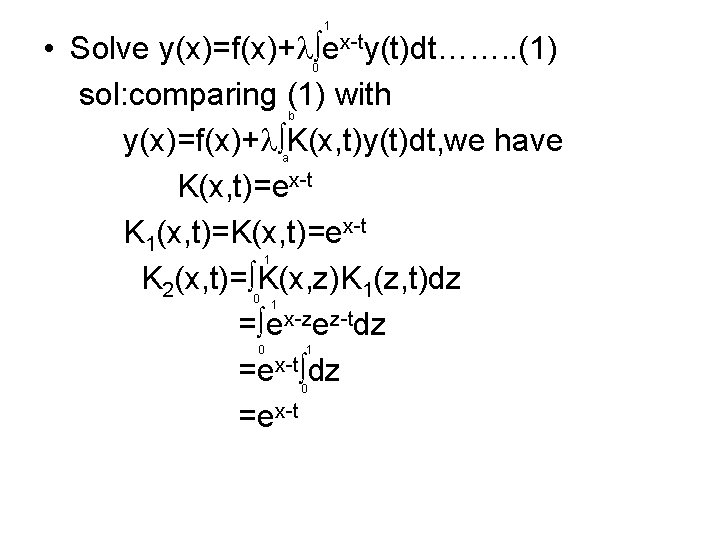



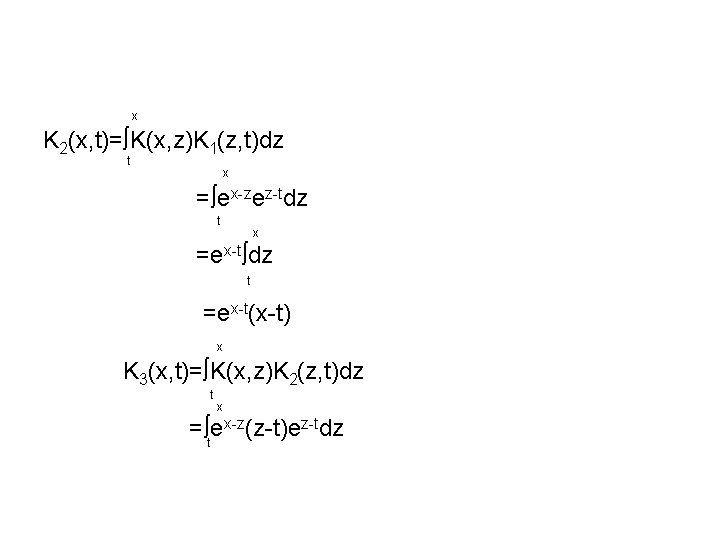


- Slides: 33

TOPIC INTEGRAL EQUATION

Definition: Integral equation An integral equation is an equation in which an unknown function appear under one or more integral signs. .

EXAMPLE For a x b, a t b, the equations b K(x, t) y(t) dt=f(x) …(1) a b y(x)- K(x, t) y(t) dt=f(x) …. (2) a where the function y(x) is the unknown function, f(x) and K(x, t) are the known functions and , a and b are constants, are all integral equations.

LINEAR INTEGRAL EQUATION An integral equation is called linear if only linear operations are perfomed in it upon the unknown function. Example: b g(x) y(x)=f(x)+ K(x, t) y(t) dt a

NON LINEAR INTEGRAL EQUATION An integral equation which is not linear is known as non linear integral equation. Example: b y(x)= K(x, t)[y(t)]2 dt where the function y(x) is the unknown function and K(x, t) is known function. a

FREDHOLM INTEGRAL EQUATION A linear integral equation of the form b g(x)y(x)=f(x)+ K(x, t) y(t) dt a where a and b are both constants f(x), g(x) and K(x, t) are known functions while y(x) is unknown function , is non zero parameter.

KINDS OF FREDHOLM INTEGRAL EQUATION 1. Fredholm integral equation of first kind 2. Fredholm integral equation of second kind 3. Fredholm integral equation of third kind

1. FREDHOLM INTEGRAL EQUATION OF FIRST KIND A linear integral equation of the form b f(x)+ K(x, t) y(t) dt=0 a is known as fredholm integral equation of first kind.

2. Fredholm integral equation of second kind A linear integral equation of the form b y(x)= f(x)+ K(x, t) y(t) dt a is known as fredholm integral equation of second kind.

3. FREDHOLM INTEGRAL EQUATION OF THIRD KIND A linear integral equation of the form b g(x)y(x)=f(x)+ K(x, t) y(t) dt a where a and b are both constants f(x), g(x) and K(x, t) are known functions while y(x) is unknown function , is non zero parameter.

HOMOGENEOUS FREDHOLM INTEGRAL EQUATION OF SECOND KIND A linear integral equation of the form b y(x)= K(x, t) y(t) dt a is known as homogeneous fredholm integral equation of second kind.

VOLTERRA INTEGRAL EQUATIONS • A linear integral equation of the form x g(x)y(x)=f(x)+ a. K(x, t) y(t) dt where upper limit of integration is variable, is called Volterra Integral equation

VOLTERRA INTEGRAL EQUATION OF THE FIRST KIND A linear integral equation of the form x f(x)+ K(x, t) y(t) dt=0 a where upper limit of integration is variable. is called Volterra integral equation of the first kind.

VOLTERRA INTEGRAL EQUATIONS OF THE SECOND KIND • A linear integral equation of the form x y(x)= f(x)+ K(x, t) y(t) dt a is called Volterra integral equation of the 2 nd kind .

HOMOGENEOUS VOLTERRA INTEGRAL EQUATIONOF 2 ND KIND • A linear integral equation of the form x y(x)= K(x, t) y(t) dt a is called homogeneous Volterra integral equation of 2 nd kind

SINGULAR INTEGRAL EQUATION • When one or both limits of integration becomes infinite or when the kernel becomes infinite at one or more points with in the range of integration , the integral equation is called singular integral equation For exampal : f(x)= (1/(x-t)α )y(t)dt, 0<α<1 x 0

Special kinds of kernels • Symmetric kernel A kernel K(x, t) is symmetric if K(x, t)=K (x, t) For exampal: sin(x+t) Separable or degenerate kernel A kernel K(x, t) is called separable if it can be expressed as the sum of finite number of terms , each of which is the product of a function of x only and a function of t only.

INTEGRAL EQUATIONS WITH SEPARABLE KERNELS • EXAMPLE • 1 : solve the fredholm integral equation of 2 nd kind y(x)=x+ (xt 2+x 2 t)y(t)dt Soln=the above equation can be written as y(x) =x+ x t 2 y(t)dt+ x 2 ty(t)dt…………(1) let C 1 = t 2 y(t)dt ………………. (2) 1 0 1 1 0 0 1 0

1 C 2= ty(t)dt…………(3) 0 using (2) and (3), (1) reduces to y(x)=x+ C 1 x+ C 2 x 2…………. (4) from (4) y(t)=t+ C 1 t+ C 2 t 2…………. . (5) using (5), (2) reduces to 1 C 1= t 2(t+ C 1 t+ C 2 t 2)dt 0 =[t 4/4+ C 1 t 4/4+ C 2 t 5/5] =1/4+ C 2/5 (20 -5 )C 1 -4 C 2=5………………. . (6) `using (5), (2) reduces to

1 C 2= t(t+ C 1 t+ C 2 t 2)dt = 1/3+ C 2/4 -4 C 1+(12 -3 )C 2=4……………(7) Solving (6)and(7) for C 1 and C 2, we get C 1=(60+ )/(240 -120 - 2) and C 2=80/(240 -120 - 2) Putting these values of C 1 and C 2 in (4), the Required solution is y(x)=x+ x(60+ )/(240 -120 - 2 )+80 x 2/(240120 - 2) =((240 -60 )x+80 x 2)/(240 -120 - 2) 0

Method of Succesive approximations

ITERATED KERNELS • For Fredholm integral equation of the second kind b y(x)=f(x)+ K(x, t) y(t) dt a The iterated kernels Kn(x, t), n=1, 2, 3…………… are defined as follows: K 1(x, t)=K(x, t) And Kn(x, t)= K(x, z)Kn-1(z, t)dz, n=2, 3, ………. . Or Kn(x, t)= Kn-1(x, z)K(z, t)dz, n=2, 3, ……. . b b a a

• For Volterra integral equation of the second kind x y(x)=f(x)+ K(x, t)y(t)dt, a The iterated kernels Kn(x, t), n=1, 2, 3, ……. are defined as follows: K 1(x, t)=K(x, t) x And Kn(x, t)= K(x, z)K n-1(z, t)dz, n=2, 3, ………. t x Or Kn(x, t)= Kn-1(x, z)K(z, t)dz, n=2, 3, … t

RESOLVENT KERNEL Suppose solution of fredholm integral equation y(x) =f(x)+ K(x, t)y(t)dt………. . (1) takes the form b a b y(x)=f(x)+ (x, t; )f(t)dt a Then (x, t; ) is known as the resolvent Kernel of (1).

Suppose solution of Volterra integral equation of the second kind y(x)=f(x)+ K(x, t)y(t)dt………. (3) takes the form x a x y(x)=f(x)+ (x, t; )f(t)dt a then (x, t, ) is known as the resolvent kernel of (3)

SOLUTION OF FREDHOLM INTEGRAL EQUATION OF SECOND KIND BY SUCCESSIVE APPROXIMATIONS
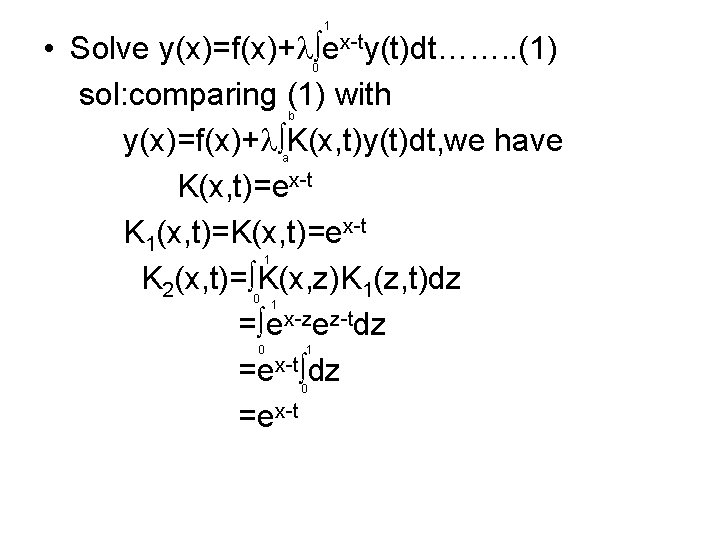
1 • Solve y(x)=f(x)+ ex-ty(t)dt……. . (1) sol: comparing (1) with y(x)=f(x)+ K(x, t)y(t)dt, we have K(x, t)=ex-t K 1(x, t)=K(x, t)=ex-t K 2(x, t)= K(x, z)K 1(z, t)dz = ex-zez-tdz =ex-t 0 b a 1 0 1 0

1 • K 3(x, t)= K(x, z)K 2(z, t)dz =ex-t Proceeding in this way, we find that all the iterated kernels coincide with K(x, t) The resolvent kernel is given by (x, t; )=ex-t(1+ + 2+……) =ex-t/(1 - ), provided | |<1 The solution is given by 0 1 y(x)=f(x)+ (x, t; )f(t)dt 0 1 =f(x)+ [ex-tf(t)/1 - ]dt where | |<1. 0

SOLUTION OF VOLTERRA INTEGRAL EQUATION OF SECOND KIND BY SUCCESSIVE APPROXIMATIONS

• Solve the integral equation X y(x)=f(x)+ ex-ty(t)dt and find the 0 resolvent kernel. Solution: Here K(x, t)=ex-t K 1(x, t)=K(x, t)=ex-t
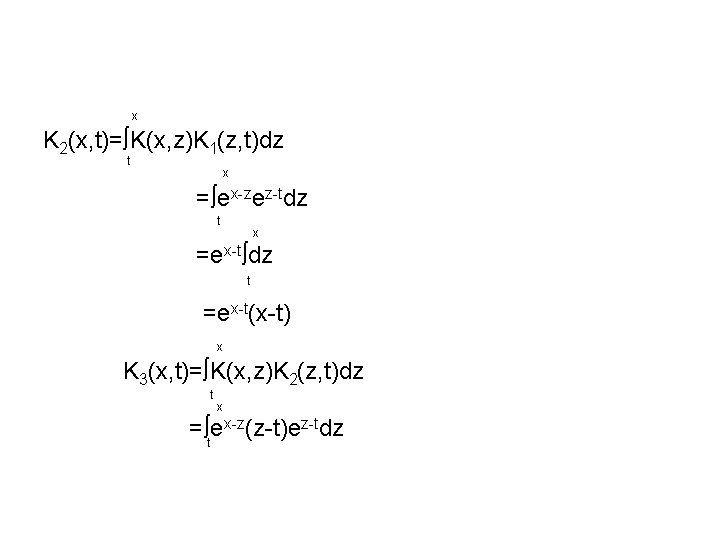
x K 2(x, t)= K(x, z)K 1(z, t)dz t x = ex-zez-tdz t x =ex-t dz t =ex-t(x-t) x K 3(x, t)= K(x, z)K 2(z, t)dz t x x-z(z-t)ez-tdz = e t

=ex-t(x-t)2/2! Proceeding in this way, we find that Kn(x, t)=(ex-t(x-t)n-1)/(n-1)!, n=1, 2, 3, ………. The resolvent kernel is (x, t; )=K 1(x, t)+ K 2(x, t)+ 2 K 3(x, t)+………. . =ex-te (x-t) =e(x-t)(1+ ) Hence the solution is X (x-t)(1+ )f(t)dt y(x)=f(x)+ e 0

TEST • Define an integral equation. How are they classified? Explain by giving an example of each type. • State and prove Fredholm altrenative theorem. • Invert the integral equation : 2 y(x)=f(x)+ (sinx cosx)y(t)dt. 0 • OR 0 Show that the integral equation 2 y(x)=f(x)+(1/ ) sin(x+t)y(t)dt 0 possesses no solution for f(x)=x, but infinitely many solutions when f(x)=1.
 Example of a clincher
Example of a clincher Topic down
Topic down Homogeneous fredholm integral equation of the second kind
Homogeneous fredholm integral equation of the second kind Difference of definite and indefinite integral
Difference of definite and indefinite integral Integral citation example
Integral citation example Blair matthews
Blair matthews Integral permukaan adalah
Integral permukaan adalah Integral foreign operation meaning
Integral foreign operation meaning Integral dx
Integral dx Topic sentence in a paragraph
Topic sentence in a paragraph Implied main idea definition
Implied main idea definition Namblaa
Namblaa Integral form of maxwell equation
Integral form of maxwell equation Integral form of maxwell equation
Integral form of maxwell equation Electric field formula
Electric field formula Fie
Fie Von karman integral
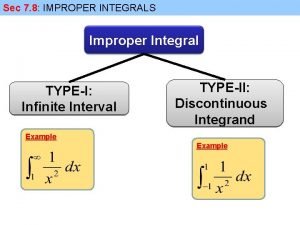
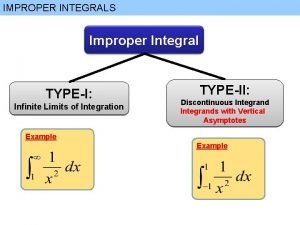
Von karman integral Definition of improper integral
Definition of improper integral Definition of improper integral
Definition of improper integral Definition definite integral
Definition definite integral The equation a + bx ® ax + b is the general equation for a
The equation a + bx ® ax + b is the general equation for a Eyring equation and arrhenius equation
Eyring equation and arrhenius equation Linear equation and quadratic equation
Linear equation and quadratic equation System of linear and quadratic equations
System of linear and quadratic equations What is euler's equation in fluid mechanics
What is euler's equation in fluid mechanics Partial differential equations formula
Partial differential equations formula Eyring equation and arrhenius equation
Eyring equation and arrhenius equation Eyring equation and arrhenius equation
Eyring equation and arrhenius equation What is net ionic reaction
What is net ionic reaction What is a topic sentence
What is a topic sentence Main idea
Main idea Sexy paragraph structure
Sexy paragraph structure What is an explanatory paragraph
What is an explanatory paragraph Worlds debate format
Worlds debate format