Chapter 23 Electric Field 23 3 Coulombs Law

Chapter 23: Electric Field 23 -3 Coulomb’s Law 23 -4 Electric Field 23 -6 Electric field lines 23 -7 Motion of charged particles in a uniform electric field Slide 1 Fig 23 CO, p. 707

INTRODUCTION Slide 2

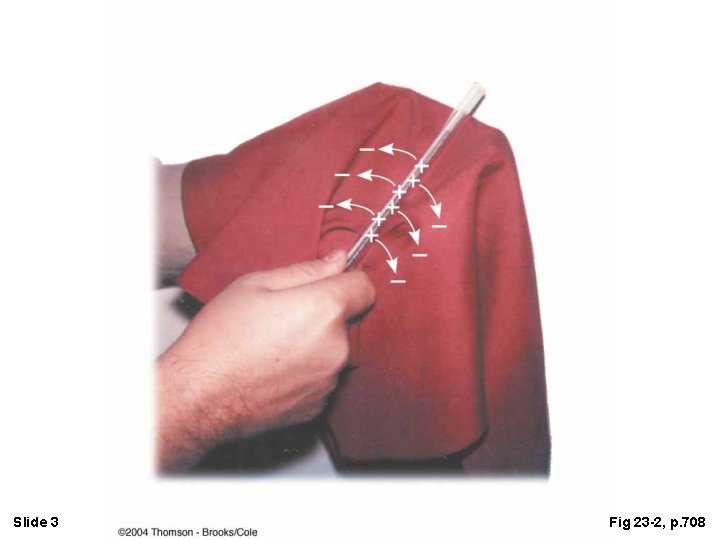
Slide 3 Fig 23 -2, p. 708

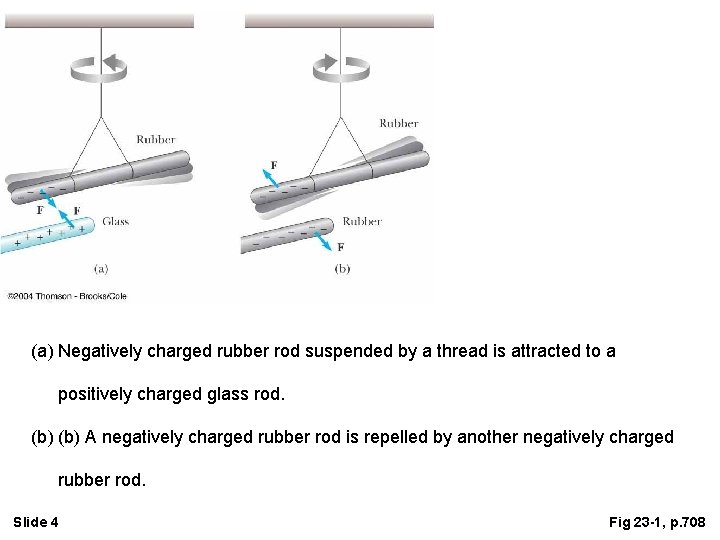
(a) Negatively charged rubber rod suspended by a thread is attracted to a positively charged glass rod. (b) A negatively charged rubber rod is repelled by another negatively charged rubber rod. Slide 4 Fig 23 -1, p. 708

Charging a metallic object by induction (that is, the two objects never touch each other). (a) A neutral metallic sphere, with equal numbers of positive and negative charges. (b) The electrons on the neutral sphere are redistributed when a charged rubber rod is placed near the sphere. (c) When the sphere is grounded, some of its electrons leave through the ground wire. (d) When the ground connection is removed, the sphere has excess positive charge that is nonuniformly distributed. Slide 5 (e) When the rod is removed, the remaining electrons redistribute uniformly and there is a net uniform distribution of positive charge on the sphere. Fig 23 -4, p. 710

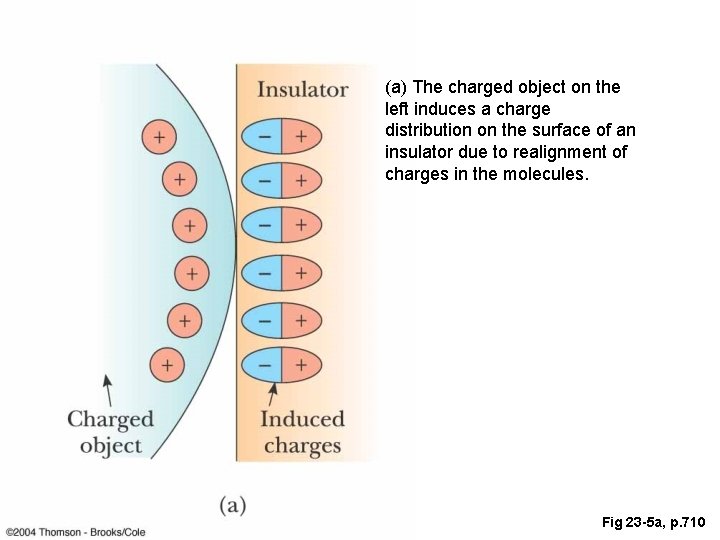
(a) The charged object on the left induces a charge distribution on the surface of an insulator due to realignment of charges in the molecules. Slide 6 Fig 23 -5 a, p. 710

Slide 7 Fig 23 -5 b, p. 710

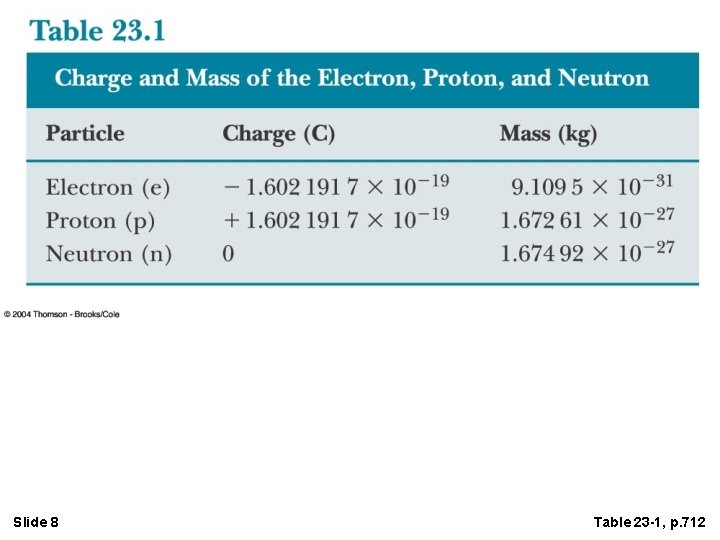
Slide 8 Table 23 -1, p. 712

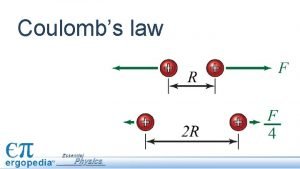
Two point charges separated by a distance r exert a force on each other that is given by Coulomb’s law. The force F 21 exerted by q 2 on q 1 is equal in magnitude and opposite in direction to the force F 12 exerted by q 1 on q 2. (a) When the charges are of the same sign, the force is repulsive. (b) When the charges are of opposite signs, the force is attractive. Slide 9 Fig 23 -7, p. 713

Slide 10 Fig 23 -7 a, p. 713

Coulomb’s experiments showed that the electric force between two stationary charged particles • is inversely proportional to the square of the separation r between the particles and directed along the line joining them; • is proportional to the product of the charges q 1 and q 2 on the two particles; • is attractive if the charges are of opposite sign and repulsive if the charges have the same sign. Slide 11 Charles Coulomb French physicist (1736– 1806)

The value of the Coulomb constant ke depends on the choice of units. The SI unit of charge is the coulomb (C). The Coulomb constant ke in SI units has the value ke = 8. 9875 x 109 N. m 2/C 2 Slide 12

The electron and proton of a hydrogen atom are separated (on the average) by a distance of approximately 5. 3 x 10 -11 m. Find the magnitudes of the electric force and the gravitational force between the two particles. Using Newton’s law of gravitation Slide 13 Thus, the gravitational force between charged atomic particles is negligible when compared with the electric force.

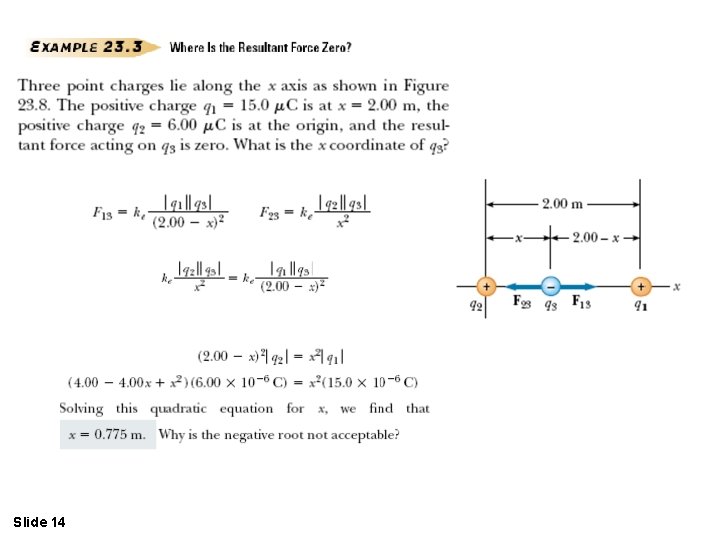
Slide 14

* The gravitational field g at a point in space, g = Fg / m. * An electric field is said to exist in the region of space around a charged object. When another charged object enters this electric field, an electric force acts on it. The vector E has the SI units of newtons per coulomb (N/C), Slide 15

Slide 16

Slide 17

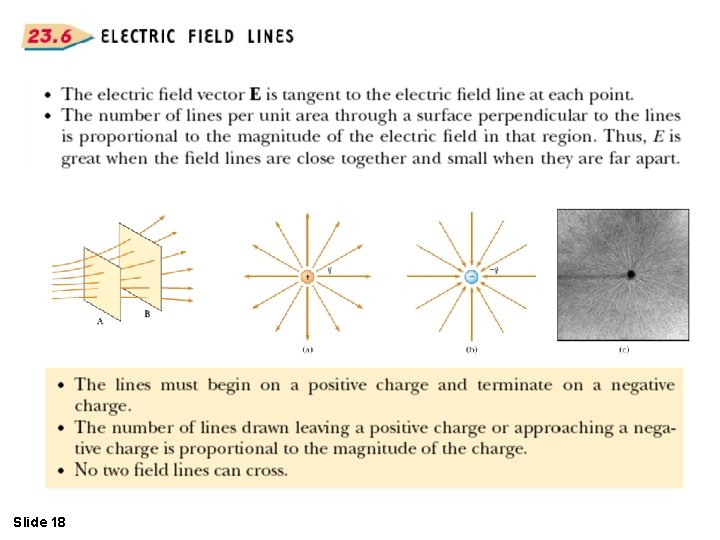
Slide 18

Slide 19

When a particle of charge q and mass m is placed in an electric field E, the electric force exerted on the charge is q. E. If this is the only force exerted on the particle, it must be the net force and so must cause the particle to accelerate. In this case, Newton’s second law applied to the particle gives; Fe = q. E = ma The acceleration of the particle is therefore a = q. E/m • If E is uniform (that is, constant in magnitude and direction), then the acceleration is constant. • If the particle has a positive charge, then its acceleration is in the direction of the electric field. • If the particle has a negative charge, then its acceleration is in the direction opposite the electric field. Slide 20

A positive point charge q of mass m is released from rest in a uniform electric field E directed along the x axis. Describe its motion. we can apply the equations of kinematics in one dimension Taking xi = 0 and vxi = o Slide 21

The kinetic energy of the charge after it has moved a distance x = xf-xi, is We can also obtain this result from the work–kinetic energy theorem because the work done by the electric force is Fex = q. Ex and W = ∆K Slide 22

An electron enters the region of a uniform electric field with vo=3. 00 x 106 m/s and E= 200 N/C. The horizontal length of the plates is l = 0. 100 m. (a) Find the acceleration of the electron while it is in the electric field. (b) Find the time it takes the electron to travel through the field. (c) What is the vertical displacement y of the electron while it is in the field? If the separation between the plates is less than this, the electron will strike the positive plate. Slide 23

Electric charges have the following important properties: • Unlike charges attract one another, and like charges repel one another. • Charge is conserved. • Charge is quantized—that is, it exists in discrete packets that are some integral multiple of the electronic charge. Conductors are materials in which charges move freely. Insulators are materials in which charges do not move freely. Slide 24

where ˆr is a unit vector directed from the charge to the point in question. The electric field is directed radially outward from a positive charge and radially inward toward a negative charge. The electric field due to a group of point charges can be obtained by using the superposition principle. That is, the total electric field at some point equals the vector sum of the electric fields of all the charges: Slide 25

Electric field lines describe an electric field in any region of space. The number of lines per unit area through a surface perpendicular to the lines is proportional to the magnitude of E in that region. A charged particle of mass m and charge q moving in an electric field E has an acceleration Slide 26

23 -7; Three point charges are located at the corners of an equilateral triangle. Calculate the net electric force on the 7. 00 u. C charge. Slide 27

23 -7; Three point charges are located at the corners of an equilateral triangle. Calculate the net electric force on the 7. 00 u. C charge. Slide 28

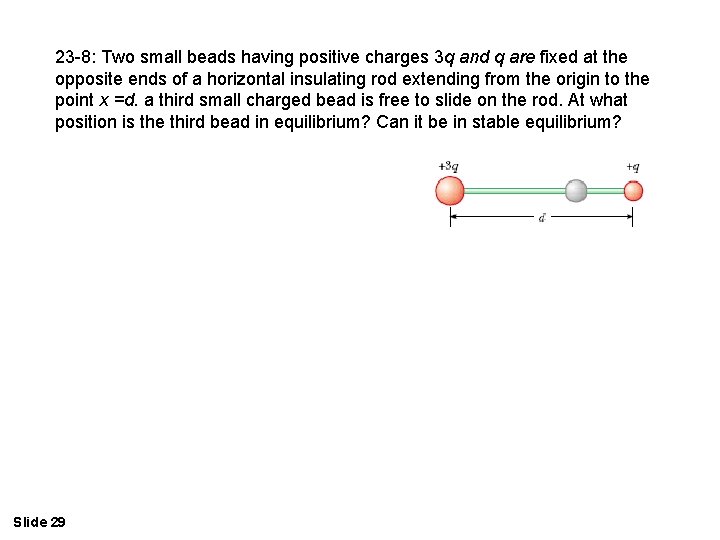
23 -8: Two small beads having positive charges 3 q and q are fixed at the opposite ends of a horizontal insulating rod extending from the origin to the point x =d. a third small charged bead is free to slide on the rod. At what position is the third bead in equilibrium? Can it be in stable equilibrium? Slide 29

23 -8: Two small beads having positive charges 3 q and q are fixed at the opposite ends of a horizontal insulating rod extending from the origin to the point x =d. a third small charged bead is free to slide on the rod. At what position is the third bead in equilibrium? Can it be in stable equilibrium? Slide 30

Problem 23 -12; An object having a net charge of 24. 0 C is placed in a uniform electric field of 610 N/C that is directed vertically. What is the mass of this object if it “floats” in the field? Slide 31

Problem 23 -12; An object having a net charge of 24. 0 C is placed in a uniform electric field of 610 N/C that is directed vertically. What is the mass of this object if it “floats” in the field? Slide 32

3 -18; Two 2. 00 u. C point charges are located on the x axis. One is at x = 1. 00 m, and the other is at x =- 1. 00 m. (a) Determine the electric field on the y axis at y =0. 500 m. (b) Calculate the electric force on a - 3. 00 u. C charge placed on the y axis at y = 0. 500 m. Slide 33

3 -18; Two 2. 00 u. C point charges are located on the x axis. One is at x = 1. 00 m, and the other is at x =- 1. 00 m. (a) Determine the electric field on the y axis at y =0. 500 m. (b) Calculate the electric force on a - 3. 00 u. C charge placed on the y axis at y = 0. 500 m. Slide 34

23 -41; An electron and a proton are each placed at rest in an electric field of 520 N/C. Calculate the speed of each particle 48. 0 ns after being released. Slide 35

23 -41; An electron and a proton are each placed at rest in an electric field of 520 N/C. Calculate the speed of each particle 48. 0 ns after being released. Slide 36

23 -44; The electrons in a particle beam each have a kinetic energy of 1. 60 x 1017 J. What are the magnitude and direction of the electric field that stops these electrons in a distance of 10. 0 cm? Slide 37

23 -44; The electrons in a particle beam each have a kinetic energy of 1. 60 x 1017 J. What are the magnitude and direction of the electric field that stops these electrons in a distance of 10. 0 cm? Slide 38

Figure 23. 27 Schematic diagram of a cathode ray tube. Electrons leaving the cathode C are accelerated to the anode A. In addition to accelerating electrons, the electron gun is also used to focus the beam of electrons, and the plates deflect the beam. Slide 41 Fig 23 -27, p. 728