Todays agenda Induced Electric Fields You must understand










- Slides: 19

Today’s agenda: Induced Electric Fields. You must understand how a changing magnetic flux induces an electric field, and be able to calculate induced electric fields. Eddy Currents. You must understand how induced electric fields give rise to circulating currents called “eddy currents. ” Displacement Current and Maxwell’s Equations. Displacement currents explain how current can flow “through” a capacitor, and how a time -varying electric field can induce a magnetic field. Back emf. A current in a coil of wire produces an emf that opposes the original current.

Time-Varying Magnetic Fields and Induced Electric Fields A Changing Magnetic Flux Produces an Electric Field? This suggests that a changing magnetic flux produces an electric field. This is true not just in conductors, but any-where in space where there is a changing magnetic flux.

The previous slide uses an equation (Mr. Ed’s) valid only for a uniform electric field. Let’s see what a more general analysis gives us. r Consider a conducting loop of radius Put your pens and pencils down and r around (but not in) a region just listen for a few minutes! where the magnetic field is into the page and increasing (e. g. , a solenoid). This could be a wire loop around the outside of a solenoid. The charged particles in the conductor are not in a magnetic field, so they experience no magnetic force. But the changing magnetic flux induces an emf around the loop.

The induced emf causes a counterclockwise current (charges move). But the magnetic field did not accelerate the charged particles (they aren’t in it). Therefore, there must be a tangential electric field around the loop. E E I r E E B is increasing. The work done moving a charged particle once around the loop is. The sign is positive because the particle’s kinetic energy increases. Remember, the magnetic force does no work when it accelerates a charged particle. If the loop has no resistance, the work done by the electric field goes into increasing the charged particle’s speed (and therefore kinetic energy). If the loop has resistance, the work done by the electric field is dissipated in the resistance (energy leaves the system).

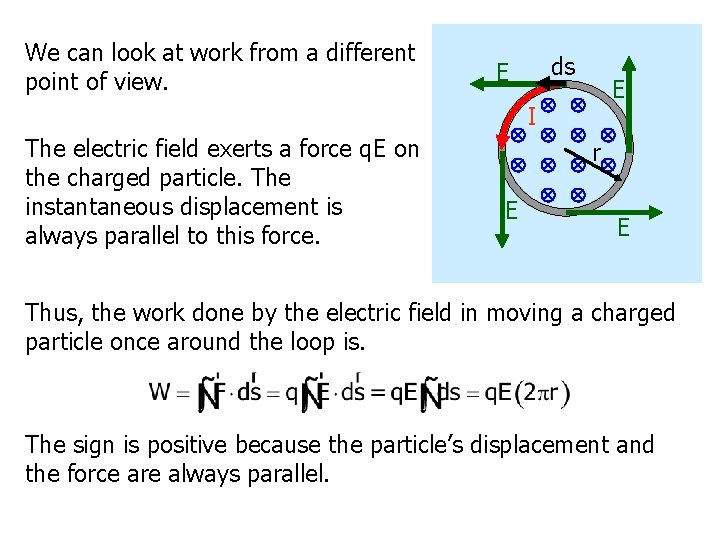
We can look at work from a different point of view. ds E E I The electric field exerts a force q. E on the charged particle. The instantaneous displacement is always parallel to this force. r E E Thus, the work done by the electric field in moving a charged particle once around the loop is. The sign is positive because the particle’s displacement and the force are always parallel.

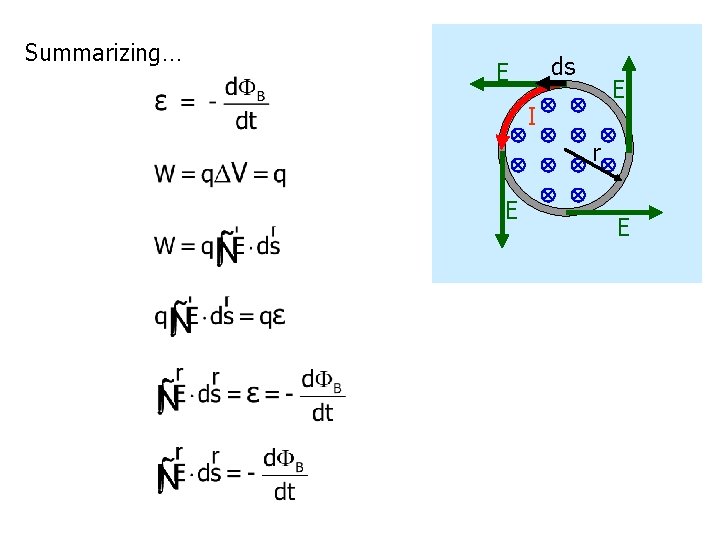
Summarizing… ds E E I r E E

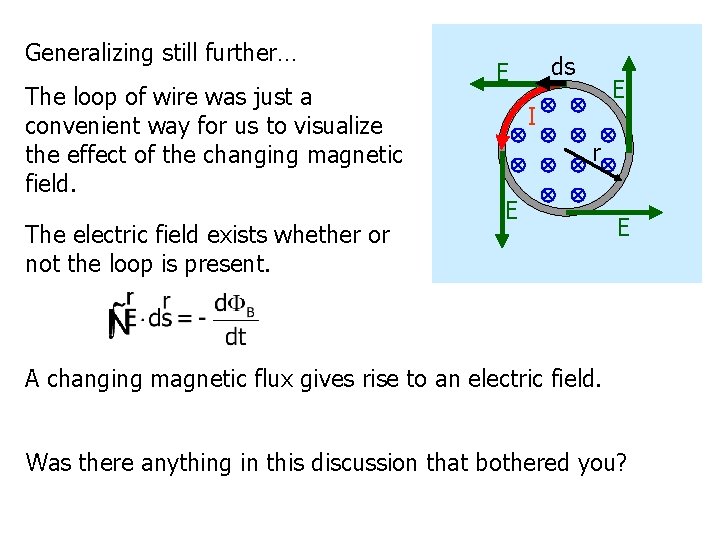
Generalizing still further… The loop of wire was just a convenient way for us to visualize the effect of the changing magnetic field. The electric field exists whether or not the loop is present. ds E E I r E E A changing magnetic flux gives rise to an electric field. Was there anything in this discussion that bothered you?

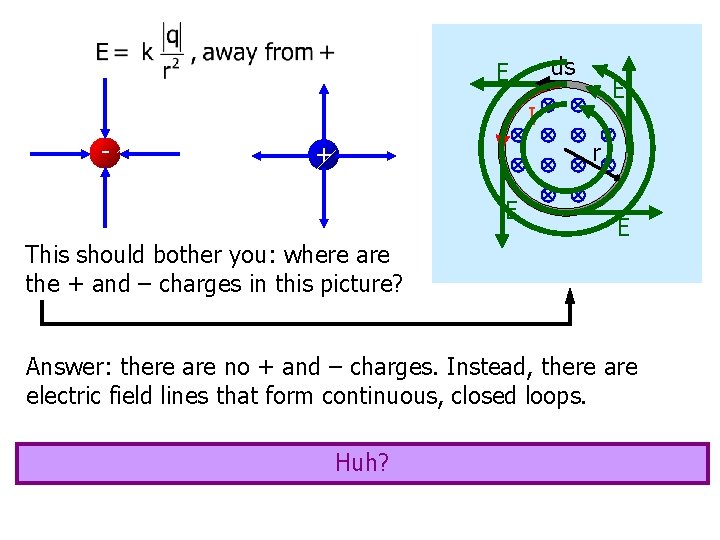
ds E E I - r + E This should bother you: where are the + and – charges in this picture? E Answer: there are no + and – charges. Instead, there are electric field lines that form continuous, closed loops. Huh?

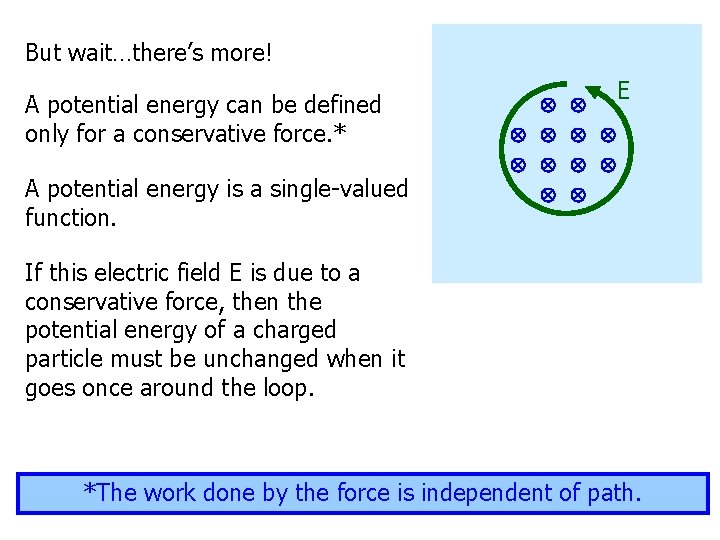
But wait…there’s more! A potential energy can be defined only for a conservative force. * A potential energy is a single-valued function. E If this electric field E is due to a conservative force, then the potential energy of a charged particle must be unchanged when it goes once around the loop. *The work done by the force is independent of path.

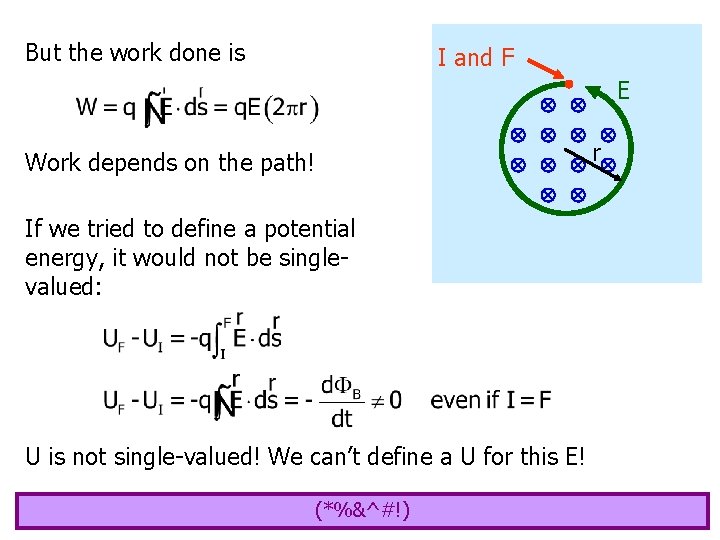
But the work done is I and F Work depends on the path! If we tried to define a potential energy, it would not be singlevalued: U is not single-valued! We can’t define a U for this E! (*%&^#!) r E

One or two of you might not have followed the discussion on the previous 9 slides. Did I confuse anybody? You can start taking notes again, if you want.

Induced Electric Fields: a summary of the key ideas A changing magnetic flux induces an electric field, as given by Faraday’s Law: This is a different manifestation of the electric field than the one you are familiar with; it is not the electrostatic field caused by the presence of stationary charged particles. Unlike the electrostatic electric field, this “new” electric field is nonconservative. “conservative, ” or “Coulomb” “nonconservative” It is better to say that there is an electric field, as described by Maxwell’s equations. We saw in lecture 17 that what an observer measures for the magnetic field depends on the motion of the observer relative to the source of the field. We see here that the same is true for the electric field. There aren’t really two different kinds of electric fields. There is just an electric field, which seems to “behave” differently depending on the relative motion of the observer and source of the field.

Stated slightly differently: we have “discovered” two different ways to generate an electric field. Coulomb Electric Field “Faraday” Electric Field Both “kinds” of electric fields are part of Maxwell’s Equations. Both “kinds” of electric fields exert forces on charged particles. The Coulomb force is conservative, the “Faraday” force is not. It is better to say that there is an electric field, as described by Maxwell’s equations. We saw in lecture 17 that what an observer measures for the magnetic field depends on the motion of the observer relative to the source of the field. We see here that the same is true for the electric field. There aren’t really two different kinds of electric fields. There is just an electric field, which seems to “behave” differently depending on the relative motion of the observer and source of the field.

Direction of Induced Electric Fields The direction of E is in the direction a positively charged particle would be accelerated by the changing flux. Use Lenz’s Law to determine the direction the changing magnetic flux would cause a current to flow. That is the direction of E.

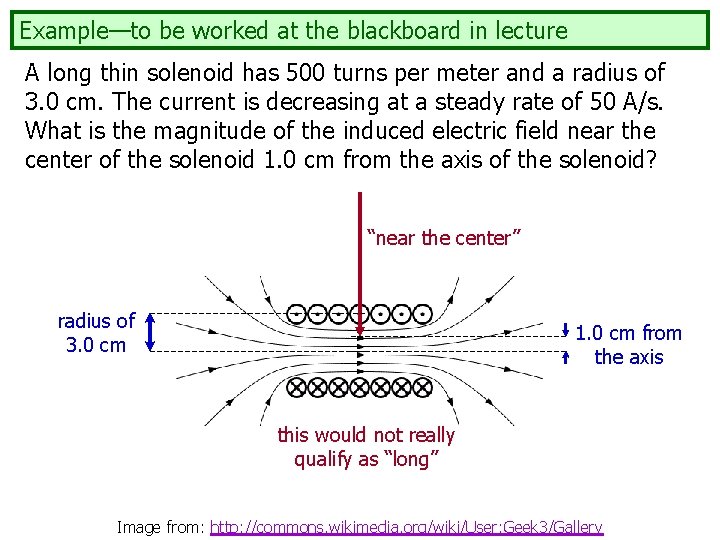
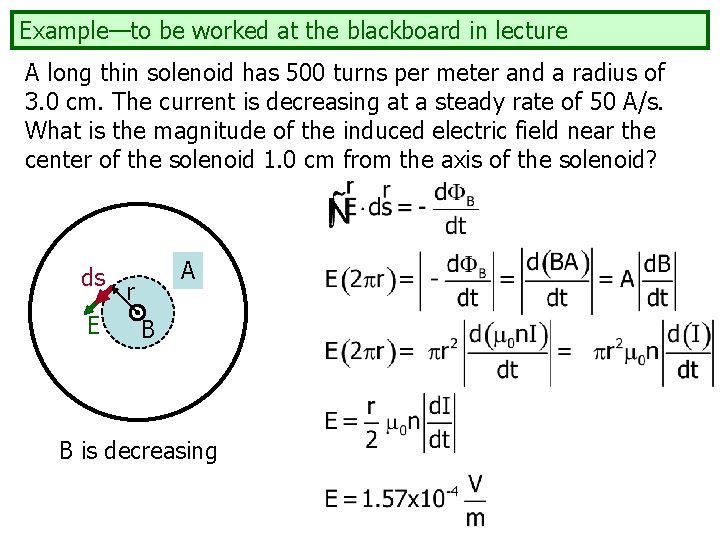
Example—to be worked at the blackboard in lecture A long thin solenoid has 500 turns per meter and a radius of 3. 0 cm. The current is decreasing at a steady rate of 50 A/s. What is the magnitude of the induced electric field near the center of the solenoid 1. 0 cm from the axis of the solenoid?

Example—to be worked at the blackboard in lecture A long thin solenoid has 500 turns per meter and a radius of 3. 0 cm. The current is decreasing at a steady rate of 50 A/s. What is the magnitude of the induced electric field near the center of the solenoid 1. 0 cm from the axis of the solenoid? “near the center” radius of 3. 0 cm 1. 0 cm from the axis this would not really qualify as “long” Image from: http: //commons. wikimedia. org/wiki/User: Geek 3/Gallery

Example—to be worked at the blackboard in lecture A long thin solenoid has 500 turns per meter and a radius of 3. 0 cm. The current is decreasing at a steady rate of 50 A/s. What is the magnitude of the induced electric field near the center of the solenoid 1. 0 cm from the axis of the solenoid? ds E A r B B is decreasing

Some Revolutionary Applications of Faraday’s Law Magnetic Tape Readers Phonograph Cartridges Electric Guitar Pickup Coils Ground Fault Interruptors Alternators Generators Transformers Electric Motors

Application of Faraday’s Law (MAE Plasma Lab) From Meeks and Rovey, Phys. Plasmas 19, 052505 (2012); doi: 10. 1063/1. 4717731. Online at http: //dx. doi. org/10. 1063/1. 4717731. T “The theta-pinch concept is one of the most widely used inductive plasma source designs ever developed. It has established a workhorse reputation within many research circles, including thin films and material surface processing, fusion, high-power space propulsion, and academia, filling the role of not only a simply constructed plasma source but also that of a key component… “Theta-pinch devices utilize relatively simple coil geometry to induce electromagnetic fields and create plasma… “This process is illustrated in Figure 1(a), which shows a cut-away of typical theta-pinch operation during an initial current rise. “FIG. 1. (a) Ideal theta-pinch field topology for an increasing current, I. ”