Chapter 21 Electric Charge and Electric Field Copyright

Chapter 21 Electric Charge and Electric Field Copyright © 2009 Pearson Education, Inc.

21 -7 Electric Field Calculations for Continuous Charge Distributions A continuous distribution of charge may be treated as a succession of infinitesimal (point) charges. The total field is then the integral of the infinitesimal fields due to each bit of charge: Remember that the electric field is a vector; you will need a separate integral for each component. Copyright © 2009 Pearson Education, Inc.

21 -7 Electric Field Calculations for Continuous Charge Distributions Example 21 -9: A ring of charge. A thin, ring-shaped object of radius a holds a total charge +Q distributed uniformly around it. Determine the electric field at a point P on its axis, a distance x from the center. Let λ be the charge per unit length (C/m). Copyright © 2009 Pearson Education, Inc.

21 -7 Electric Field Calculations for Continuous Charge Distributions Conceptual Example 21 -10: Charge at the center of a ring. Imagine a small positive charge placed at the center of a nonconducting ring carrying a uniformly distributed negative charge. Is the positive charge in equilibrium if it is displaced slightly from the center along the axis of the ring, and if so is it stable? What if the small charge is negative? Neglect gravity, as it is much smaller than the electrostatic forces. Copyright © 2009 Pearson Education, Inc.

Symmetry If the problem has symmetry, then the solution MUST have the same symmetry: • Planar • Cylindrical • Spherical Copyright © 2009 Pearson Education, Inc.

21 -7 Electric Field Calculations for Continuous Charge Distributions Example 21 -11: Long line of charge. Determine the magnitude of the electric field at any point P a distance x from a very long line (a wire, say) of uniformly distributed charge. Assume x is much smaller than the length of the wire, and let λ be the charge per unit length (C/m). Copyright © 2009 Pearson Education, Inc.

21 -7 Electric Field Calculations for Continuous Charge Distributions Example 21 -12: Uniformly charged disk. Charge is distributed uniformly over a thin circular disk of radius R. The charge per unit area (C/m 2) is σ. Calculate the electric field at a point P on the axis of the disk, a distance z above its center. Copyright © 2009 Pearson Education, Inc.

21 -7 Electric Field Calculations for Continuous Charge Distributions In the previous example, if we are very close to the disk (that is, if z << R), the electric field is: This is the field due to an infinite plane of charge. Copyright © 2009 Pearson Education, Inc.

21 -7 Electric Field Calculations for Continuous Charge Distributions Example 21 -13: Two parallel plates. Determine the electric field between two large parallel plates or sheets, which are very thin and are separated by a distance d which is small compared to their height and width. One plate carries a uniform surface charge density σ and the other carries a uniform surface charge density -σ as shown (the plates extend upward and downward beyond the part shown). Copyright © 2009 Pearson Education, Inc.

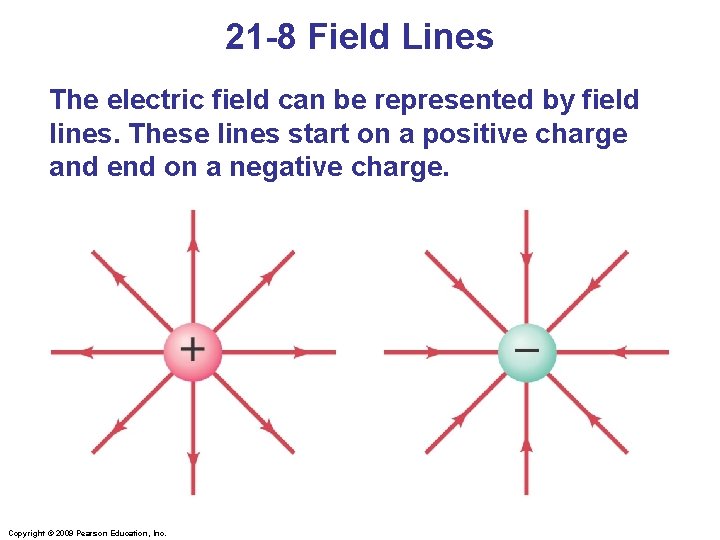
21 -8 Field Lines The electric field can be represented by field lines. These lines start on a positive charge and end on a negative charge. Copyright © 2009 Pearson Education, Inc.

21 -8 Field Lines The number of field lines starting (ending) on a positive (negative) charge is proportional to the magnitude of the charge. The electric field is stronger where the field lines are closer together. Drawings are schematic only; real world is 3 dimensional, not 2 -dimensional Copyright © 2009 Pearson Education, Inc.

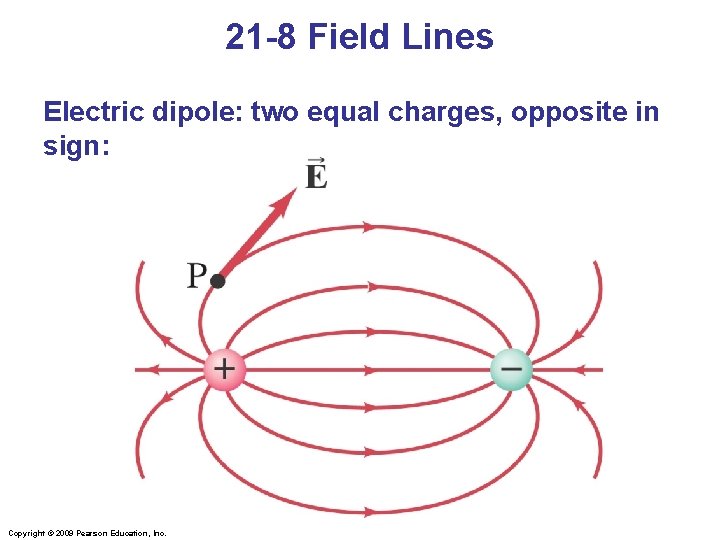
21 -8 Field Lines Electric dipole: two equal charges, opposite in sign: Copyright © 2009 Pearson Education, Inc.

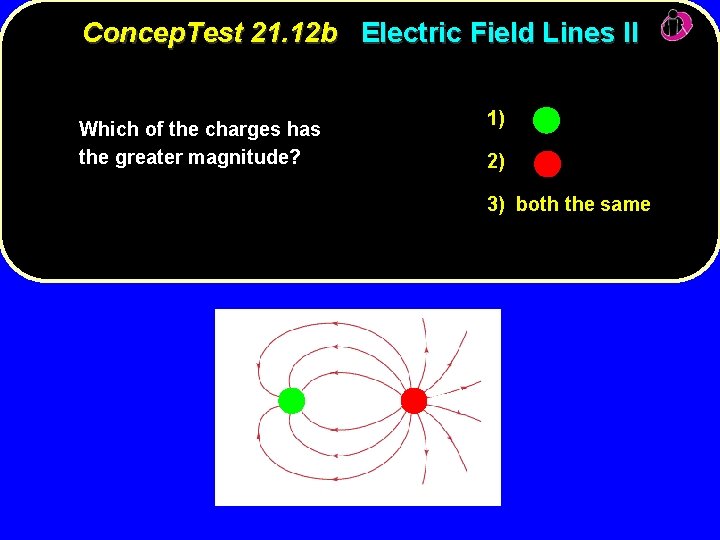
Concep. Test 21. 12 a Electric Field Lines I 1) What are the signs of the charges whose electric fields are shown at right? 2) 3) 4) 5) no way to tell

Concep. Test 21. 12 a Electric Field Lines I 1) What are the signs of the charges whose electric fields are shown at right? 2) 3) 4) 5) no way to tell Electric field lines originate on positive charges and terminate on negative charges

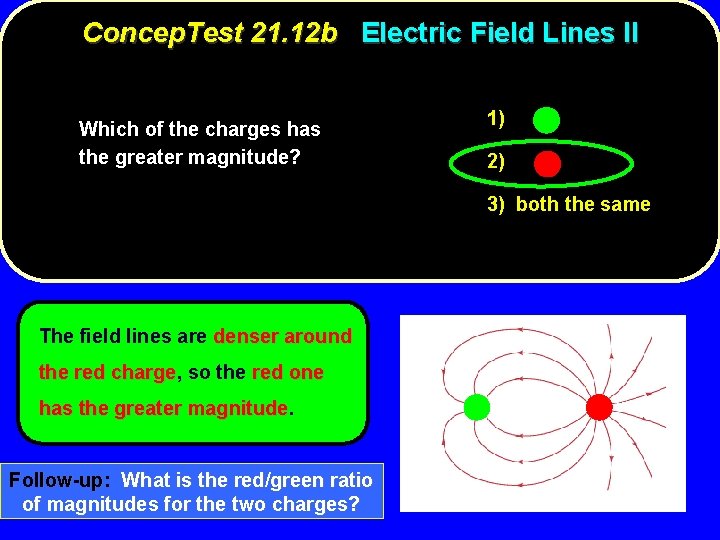
Concep. Test 21. 12 b Electric Field Lines II Which of the charges has the greater magnitude? 1) 2) 3) both the same

Concep. Test 21. 12 b Electric Field Lines II Which of the charges has the greater magnitude? 1) 2) 3) both the same The field lines are denser around the red charge, charge so the red one has the greater magnitude Follow-up: What is the red/green ratio of magnitudes for the two charges?

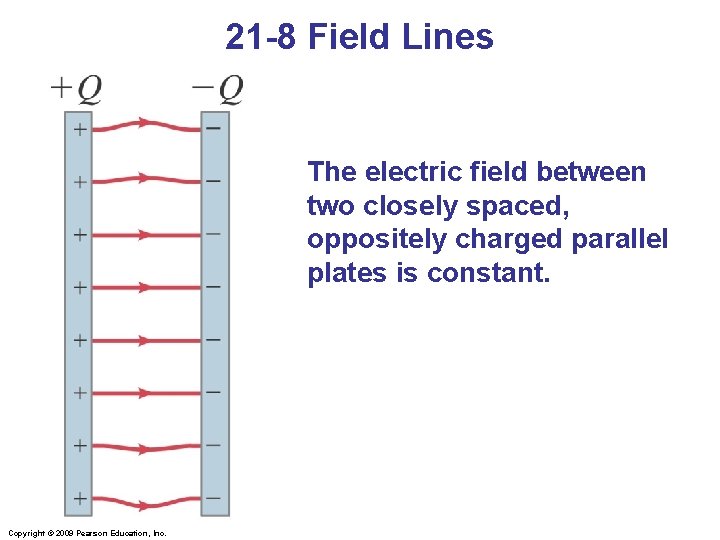
21 -8 Field Lines The electric field between two closely spaced, oppositely charged parallel plates is constant. Copyright © 2009 Pearson Education, Inc.

21 -8 Field Lines Summary of field lines: 1. Field lines indicate the direction of the field; the field is tangent to the line. 2. The magnitude of the field is proportional to the density of the lines. 3. Field lines start on positive charges and end on negative charges; the number is proportional to the magnitude of the charge. Copyright © 2009 Pearson Education, Inc.

21 -9 Electric Fields and Conductors The static electric field inside a conductor is zero – if it were not, the charges would move. The net charge on a conductor resides on its outer surface. Copyright © 2009 Pearson Education, Inc.

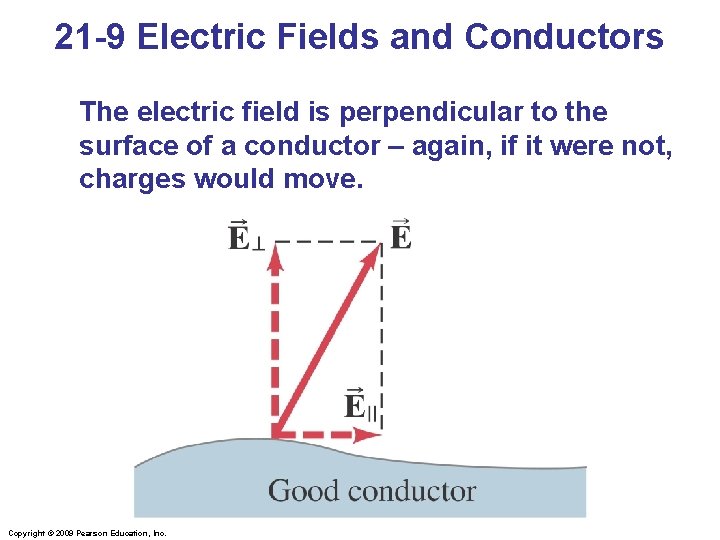
21 -9 Electric Fields and Conductors The electric field is perpendicular to the surface of a conductor – again, if it were not, charges would move. Copyright © 2009 Pearson Education, Inc.

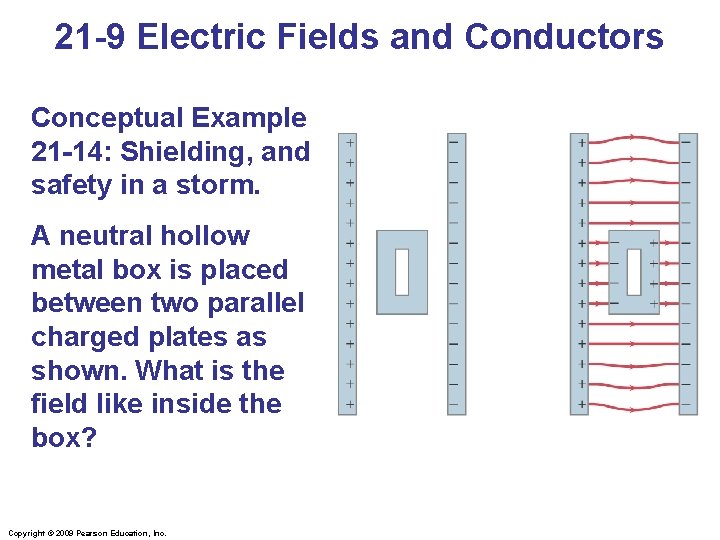
21 -9 Electric Fields and Conductors Conceptual Example 21 -14: Shielding, and safety in a storm. A neutral hollow metal box is placed between two parallel charged plates as shown. What is the field like inside the box? Copyright © 2009 Pearson Education, Inc.

21 -10 Motion of a Charged Particle in an Electric Field The force on an object of charge q in an electric field is given by: =q Therefore, if we know the mass and charge of a particle, we can describe its subsequent motion in an electric field. Copyright © 2009 Pearson Education, Inc.

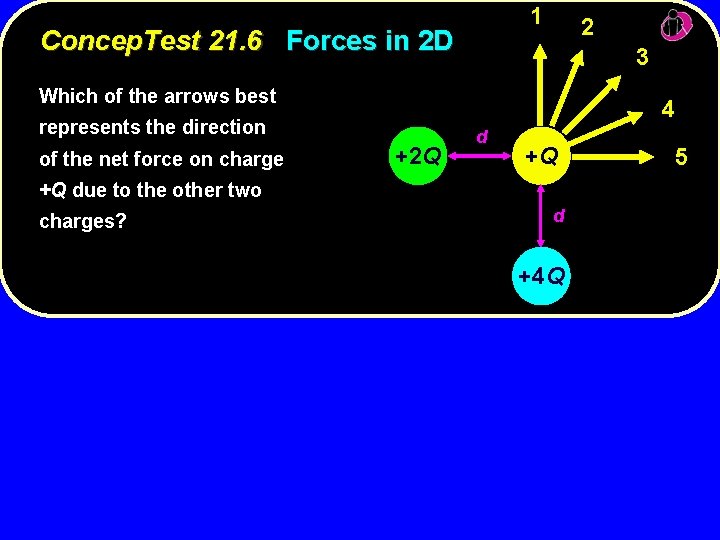
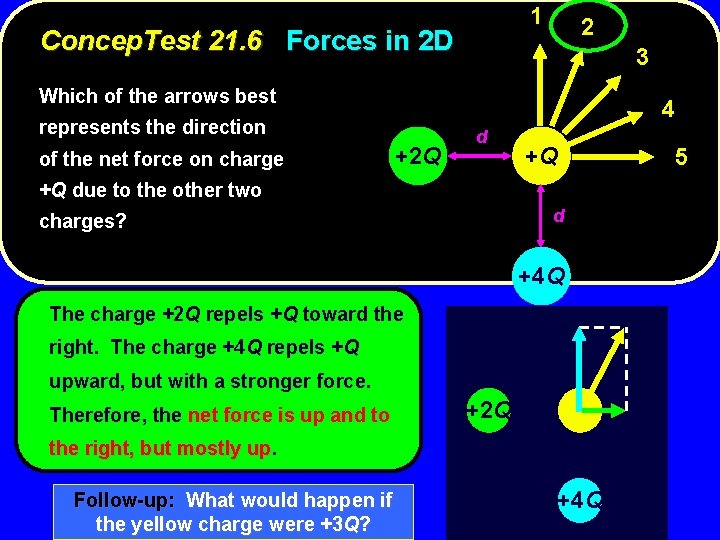
1 Concep. Test 21. 6 Forces in 2 D 2 3 Which of the arrows best 4 represents the direction of the net force on charge +2 Q d +Q +Q due to the other two charges? d +4 Q 5

1 Concep. Test 21. 6 Forces in 2 D 2 3 Which of the arrows best 4 represents the direction of the net force on charge +2 Q d +Q +Q due to the other two d charges? +4 Q The charge +2 Q repels +Q toward the right. The charge +4 Q repels +Q upward, but with a stronger force. Therefore, the net force is up and to +2 Q the right, but mostly up. up Follow-up: What would happen if the yellow charge were +3 Q? +4 Q 5

21 -10 Motion of a Charged Particle in an Electric Field Example 21 -15: Electron accelerated by electric field. An electron (mass m = 9. 11 x 10 -31 kg) is accelerated in the uniform field (E = 2. 0 x 104 N/C) between two parallel charged plates. The separation of the plates is 1. 5 cm. The electron is accelerated from rest near the negative plate and passes through a tiny hole in the positive plate. (a) With what speed does it leave the hole? (b) Show that the gravitational force can be ignored. Assume the hole is so small that it does not affect the uniform field between the plates. Copyright © 2009 Pearson Education, Inc.

21 -10 Motion of a Charged Particle in an Electric Field Example 21 -16: Electron moving perpendicular to. Suppose an electron traveling with speed v 0 = 1. 0 x 107 m/s enters a uniform electric field , which is at right angles to v 0 as shown. Describe its motion by giving the equation of its path while in the electric field. Ignore gravity. Copyright © 2009 Pearson Education, Inc.

21 -11 Electric Dipoles An electric dipole consists of two charges Q, equal in magnitude and opposite in sign, separated by a distance. The dipole moment, p = Q , points from the negative to the positive charge. Copyright © 2009 Pearson Education, Inc.

21 -11 Electric Dipoles An electric dipole in a uniform electric field will experience no net force, but it will, in general, experience a torque: Copyright © 2009 Pearson Education, Inc.

21 -11 Electric Dipoles The electric field created by a dipole is the sum of the fields created by the two charges; far from the dipole, the field shows a 1/r 3 dependence: Copyright © 2009 Pearson Education, Inc.

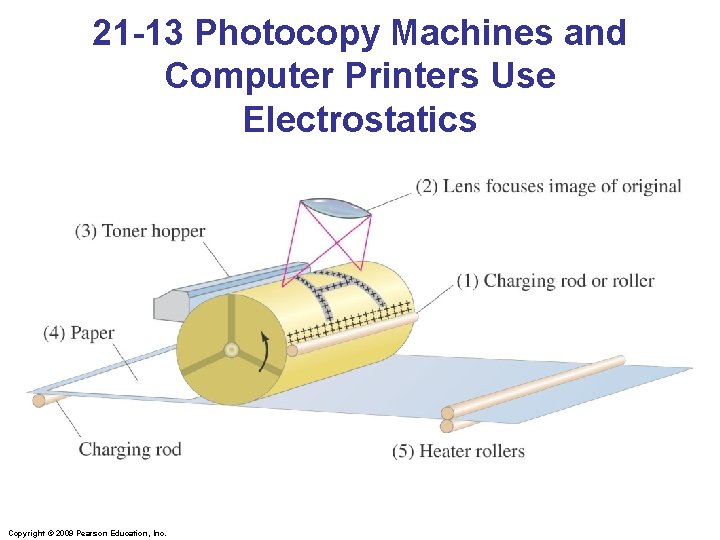
21 -13 Photocopy Machines and Computer Printers Use Electrostatics Photocopy machine: • drum is charged positively • image is focused on drum • only black areas stay charged and therefore attract toner particles • image is transferred to paper and sealed by heat Copyright © 2009 Pearson Education, Inc.

21 -13 Photocopy Machines and Computer Printers Use Electrostatics Copyright © 2009 Pearson Education, Inc.

21 -13 Photocopy Machines and Computer Printers Use Electrostatics Laser printer is similar, except a computer controls the laser intensity to form the image on the drum. Copyright © 2009 Pearson Education, Inc.

Summary of Chapter 21 • Two kinds of electric charge – positive and negative. • Charge is conserved. • Charge on electron: e = 1. 602 x 10 -19 C. • Conductors: electrons free to move. • Insulators: nonconductors. Copyright © 2009 Pearson Education, Inc.

Summary of Chapter 21 • Charge is quantized in units of e. • Objects can be charged by conduction or induction. • Coulomb’s law: • Electric field is force per unit charge: Copyright © 2009 Pearson Education, Inc.

Summary of Chapter 21 • Electric field of a point charge: • Electric field can be represented by electric field lines. • Static electric field inside conductor is zero; surface field is perpendicular to surface. Copyright © 2009 Pearson Education, Inc.

Chapter 22 Gauss’s Law Copyright © 2009 Pearson Education, Inc.

Units of Chapter 22 • Electric Flux • Gauss’s Law • Applications of Gauss’s Law • Experimental Basis of Gauss’s and Coulomb’s Laws Copyright © 2009 Pearson Education, Inc.

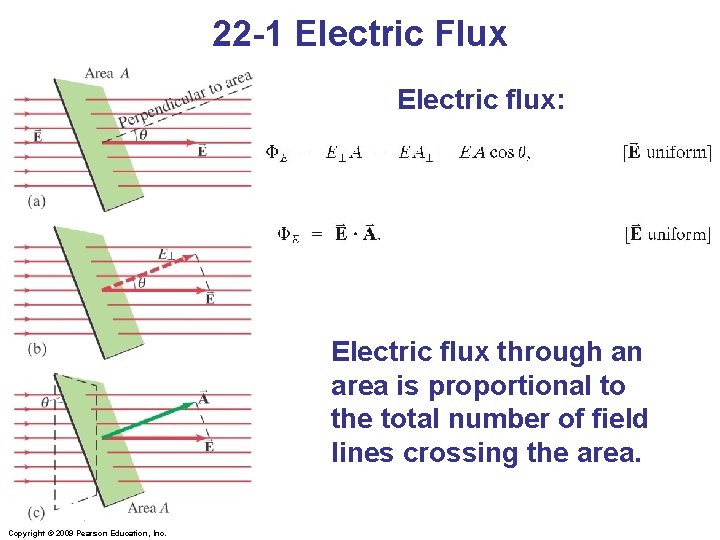
22 -1 Electric Flux Electric flux: Electric flux through an area is proportional to the total number of field lines crossing the area. Copyright © 2009 Pearson Education, Inc.

22 -1 Electric Flux Example 22 -1: Electric flux. Calculate the electric flux through the rectangle shown. The rectangle is 10 cm by 20 cm, the electric field is uniform at 200 N/C, and the angle θ is 30°. Copyright © 2009 Pearson Education, Inc.

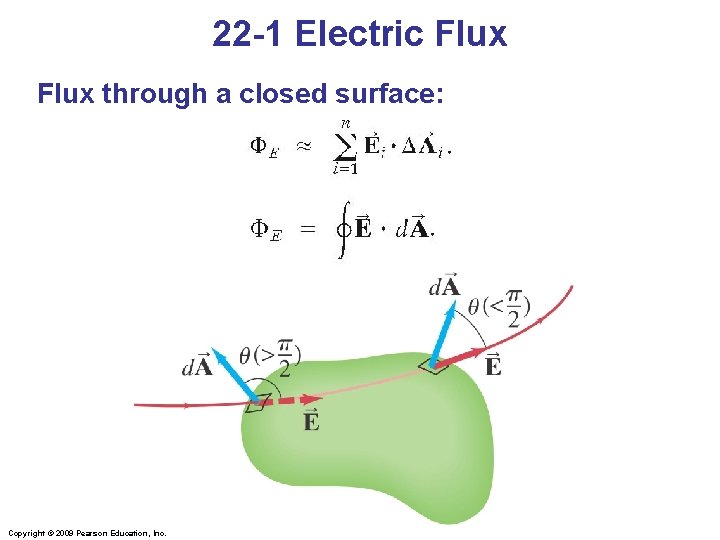
22 -1 Electric Flux through a closed surface: Copyright © 2009 Pearson Education, Inc.

22 -2 Gauss’s Law The net number of field lines through the surface is proportional to the charge enclosed, and also to the flux, giving Gauss’s law: This can be used to find the electric field in situations with a high degree of symmetry. Copyright © 2009 Pearson Education, Inc.

22 -2 Gauss’s Law For a point charge, Therefore, Solving for E gives the result we expect from Coulomb’s law: Copyright © 2009 Pearson Education, Inc.

22 -2 Gauss’s Law Using Coulomb’s law to evaluate the integral of the field of a point charge over the surface of a sphere surrounding the charge gives: Looking at the arbitrarily shaped surface A 2, we see that the same flux passes through it as passes through A 1. Therefore, this result should be valid for any closed surface. Copyright © 2009 Pearson Education, Inc.

22 -2 Gauss’s Law Finally, if a gaussian surface encloses several point charges, the superposition principle shows that: Therefore, Gauss’s law is valid for any charge distribution. Note, however, that it only refers to the field due to charges within the gaussian surface – charges outside the surface will also create fields. Copyright © 2009 Pearson Education, Inc.

22 -2 Gauss’s Law Conceptual Example 22 -2: Flux from Gauss’s law. Consider the two gaussian surfaces, A 1 and A 2, as shown. The only charge present is the charge Q at the center of surface A 1. What is the net flux through each surface, A 1 and A 2? Copyright © 2009 Pearson Education, Inc.

22 -3 Applications of Gauss’s Law Example 22 -3: Spherical conductor. A thin spherical shell of radius r 0 possesses a total net charge Q that is uniformly distributed on it. Determine the electric field at points (a) outside the shell, and (b) within the shell. (c) What if the conductor were a solid sphere? Copyright © 2009 Pearson Education, Inc.

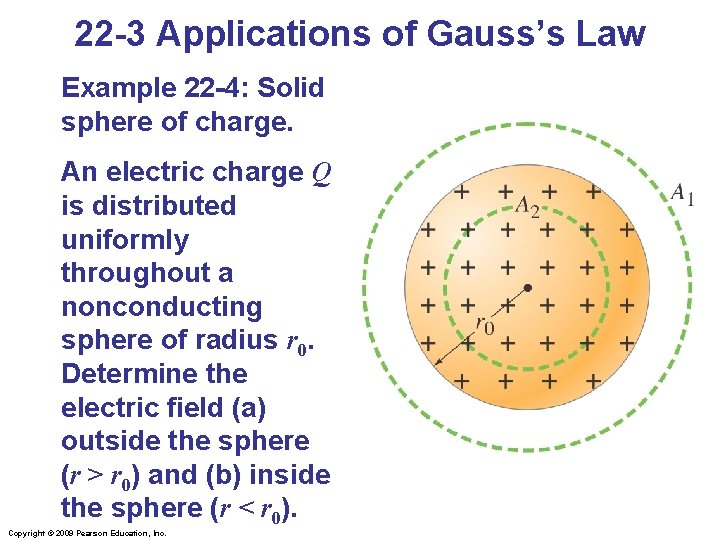
22 -3 Applications of Gauss’s Law Example 22 -4: Solid sphere of charge. An electric charge Q is distributed uniformly throughout a nonconducting sphere of radius r 0. Determine the electric field (a) outside the sphere (r > r 0) and (b) inside the sphere (r < r 0). Copyright © 2009 Pearson Education, Inc.

22 -3 Applications of Gauss’s Law Example 22 -6: Long uniform line of charge. A very long straight wire possesses a uniform positive charge per unit length, λ. Calculate the electric field at points near (but outside) the wire, far from the ends. Copyright © 2009 Pearson Education, Inc.

22 -3 Applications of Gauss’s Law Example 22 -7: Infinite plane of charge. Charge is distributed uniformly, with a surface charge density σ (σ = charge per unit area = d. Q/d. A) over a very large but very thin nonconducting flat plane surface. Determine the electric field at points near the plane. Copyright © 2009 Pearson Education, Inc.

22 -3 Applications of Gauss’s Law Example 22 -8: Electric field near any conducting surface. Show that the electric field just outside the surface of any good conductor of arbitrary shape is given by E = σ/ε 0 where σ is the surface charge density on the conductor’s surface at that point. Copyright © 2009 Pearson Education, Inc.

22 -3 Applications of Gauss’s Law Conceptual Example 22 -9: Conductor with charge inside a cavity. Suppose a conductor carries a net charge +Q and contains a cavity, inside of which resides a point charge +q. What can you say about the charges on the inner and outer surfaces of the conductor? Copyright © 2009 Pearson Education, Inc.

22 -3 Applications of Gauss’s Law Procedure for Gauss’s law problems: 1. Identify the symmetry, and choose a gaussian surface that takes advantage of it (with surfaces along surfaces of constant field). 2. Draw the surface. 3. Use the symmetry to find the direction of E. 4. Evaluate the flux by integrating. 5. Calculate the enclosed charge. 6. Solve for the field. Copyright © 2009 Pearson Education, Inc.

22 -4 Experimental Basis of Gauss’s and Coulomb’s Laws In the experiment shown, Gauss’s law predicts that the charge on the ball flows onto the surface of the cylinder when they are in contact. This can be tested by measuring the charge on the ball after it is removed – it should be zero. Copyright © 2009 Pearson Education, Inc.

Summary of Chapter 22 • Electric flux: • Gauss’s law can be used to calculate the field in situations with a high degree of symmetry. • Gauss’s law applies in all situations, and therefore is more general than Coulomb’s law. Copyright © 2009 Pearson Education, Inc.