Coulombs Law Lecture3 Coulombs Law Like charges repel

Coulombs Law Lecture-3

Coulombs Law Like charges repel, unlike charges attract. The electric force acting on a point charge q 1 as a result of the presence of a second point charge q 2 is given by Coulomb's Law: where e 0 = permittivity of space

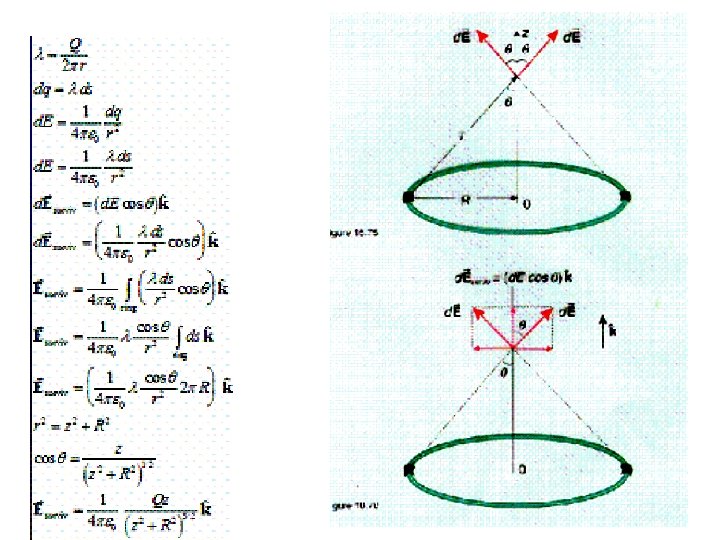
Quiz • A charge Q 1= 1 n. C is located at the origin in free space and another charge Q at (2, 0, 0). If the X – component of the electric field at (3, 1, 1) is zero, calculate the value of Q. Is the Y component zero at (3, 1, 1)? Ans: -3(3/11)1. 5 Q 1 Calculation of E: due to 1. Dipole, 2. Rod (line charge), Ring (Line charge), 3. Circular plate (surface charge), Square sheet, 4. Sphere or Cylinder (Volume charge density)

Gauss's Law • The total of the electric flux out of a closed surface is equal to the charge enclosed divided by the permittivity. • Electric Flux over a Closed Surface = Charge enclosed by the Surface divided by eo. da Φ= • +q eo = the permittivity of free space 8. 854 x 10 -12 C 2/(N m 2) = 1/4 pk) E

Case(i) Charge is placed inside the body: da * Flux passing through an area da: E +q Total flux over a closed surface: Where dΩ is solid angle da E da cosθ +q dΩ

Case(ii) Charge is placed outside the surface • Flux passing through AB: da +q • Flux passing through CD: A da B C E D Where dΩ is solid angle Net flux = 0 where Note: dΩ will remain same for but direction of the flux will be opposite. da E

• A more intuitive statement: the total number of electric field lines entering or leaving a closed volume of space is directly proportional to the charge enclosed by the volume • If there is no net charge inside some volume of space then the electric flux over the surface of that volume is always equal to zero. . Electric Flux: The Electric Flux FE is the product of Component of the Electric Field Perpendicular to a surface times the surface area.
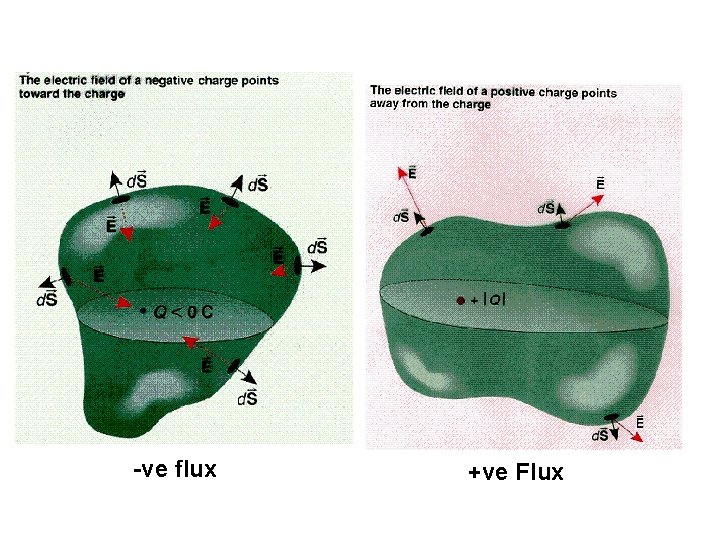
-ve flux +ve Flux

Differential form of Gauss Law: Proof: Gauss Law Φ= Gauss divergence theorem: or Where D=ε 0 E, called Electric field displacement vector. Note: Gauss law is also known as Maxwell’s first equation.

Quiz: 1. 2. 3. 4. How electric flux is related to number of electric field lines? How will you determine flux for nonuniform surfaces? How will you explain negative flux or positive flux? A positive charge of 1 μC is placed at the centre of a hollow cube. Calculate the electric flux diverging 1. 2. 5. through the cube. through each face. Ans: 1. 12 x 105 V/m Ans: 1. 86 x 104 V/m If E=3 i+4 j-5 k, calculate electric flux through the surface S=2 x 10 -5 k m 2. Ans: -10 -4 V/m

Applications of Gauss law Lecture-4

(Spherical systems: Conducting Sphere) 1)Conducting Sphere of charge ‘q’ and radius ‘R’: 1) E at an external point: Eo r>R 2) E at the surface: Es r=R 3) E at an internal point: Ei r<R Gaussian surface Case-I: E at an external point; Net electric fux through ‘P’: R P r S 1 The Electric field strength at any point outside a spherical charge distribution is the same as through the whole charge were concentrated at the centre.
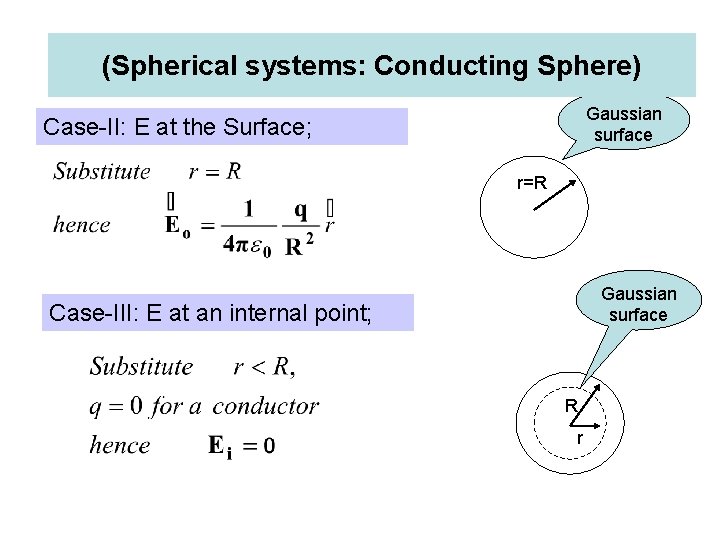
(Spherical systems: Conducting Sphere) Gaussian surface Case-II: E at the Surface; r=R Gaussian surface Case-III: E at an internal point; R r
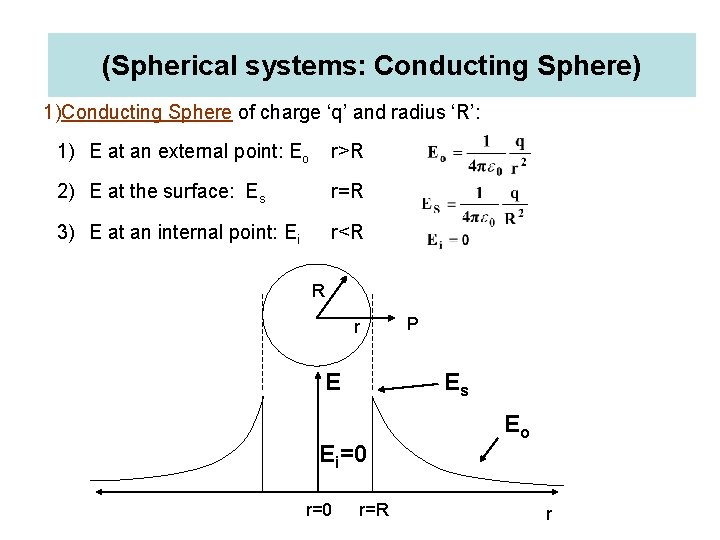
(Spherical systems: Conducting Sphere) 1)Conducting Sphere of charge ‘q’ and radius ‘R’: 1) E at an external point: Eo r>R 2) E at the surface: Es r=R 3) E at an internal point: Ei r<R R r E Es Ei=0 r=0 P r=R Eo r

(Spherical systems: Nonconducting Sphere) Nonconducting sphere (Volume charge density) • E at an external point: Eo • E at the surface: Es • E at an internal point: Ei

(Spherical systems: Nonconducting Sphere) 1)Nonconducting Sphere of charge ‘q’ and radius ‘R’: 1) E at an external point: Eo r>R Volume charge density 2) E at the surface: Es r=R 3) E at an internal point: Ei r<R Case-I: E at an external point; Net electric flux through ‘P’: Gaussian surface R P r S 1

(Spherical systems: Nonconducting Sphere) Gaussian surface Case-II: E at the Surface; r=R Case-II: E at an internal point; Gaussian surface R r
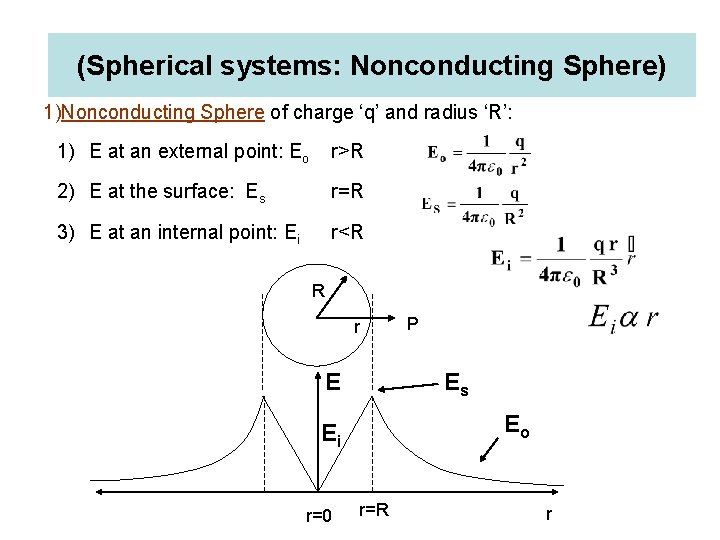
(Spherical systems: Nonconducting Sphere) 1)Nonconducting Sphere of charge ‘q’ and radius ‘R’: 1) E at an external point: Eo r>R 2) E at the surface: Es r=R 3) E at an internal point: Ei r<R R r E Es Eo Ei r=0 P r=R r

Applications of Gauss law (Cylindrical distribution systems)

Applications of Gauss law (Cylindrical distribution systems) 1)Conducting long Cylinder of charge ‘q’ and radius ‘R’: 1) E at an external point: Eo 2) E at the surface: Es 3) E at an internal point: Ei 2)Nonconducting long Cylinder 1) E at an external point: Eo 2) E at the surface: Es 3) E at an internal point: Ei

Cylindrical distribution systems: Conducting Cylinder 1)Conducting long Cylinder of charge ‘q’ and radius ‘R’ : 1) E at an external point: Eo r>R 2) E at the surface: Es r=R 3) E at an internal point: Ei r<R Gaussian surface Case-I: E at an external point; Net electric flux through ‘P’: l E R O P r
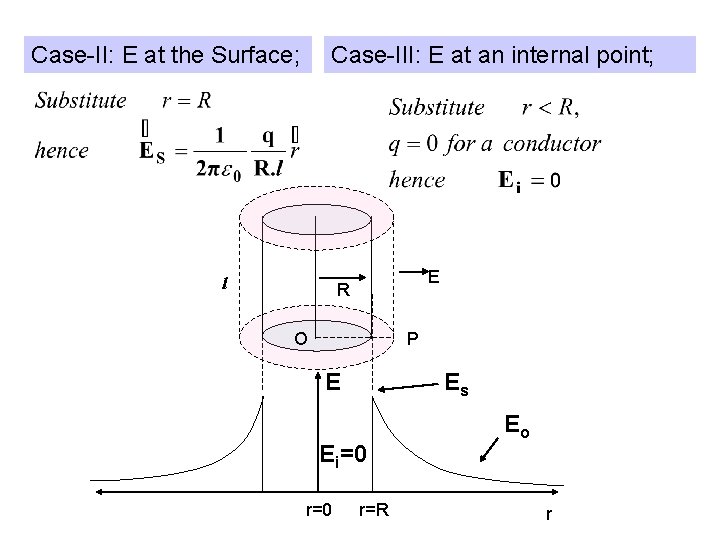
Case-II: E at the Surface; Case-III: E at an internal point; l E R O P E Es Ei=0 r=R Eo r

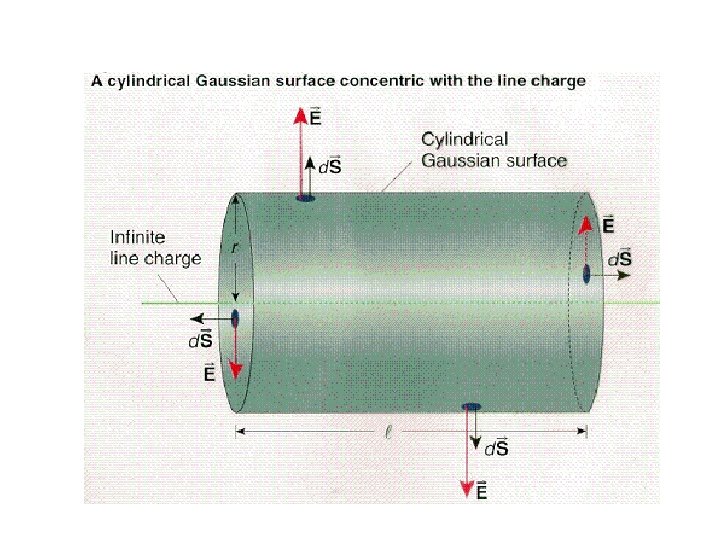
For infinite long line charge density ‘λ’

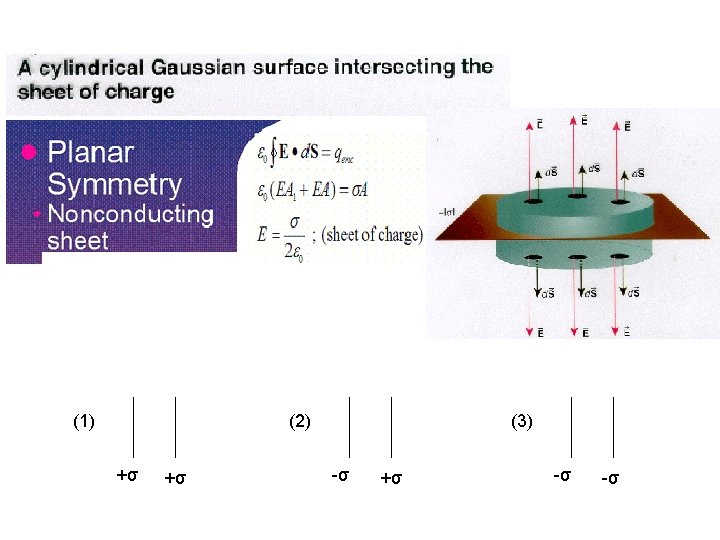
Applications of Gauss law (Infinitely long sheet of Charge)

Quiz • For a conducting sphere: with surface charge density ‘σ’ and radius R, determine Eo, Es and Ei. • For a spherical shell volume charge density is ρ=k/r 2 for a≤r≤b otherwise zero. determine E for each region. • For a cylinder of radius ‘R’ and height ‘h’ volume charge density is ρ=kr. Determine Eo, Es and Ei

Electric field in inside and just outside (very close) of the surface of a charged conductor • Ans: Inside E=0, Outside E= σ/ε 0
- Slides: 29