Physics 014 Chapter 22 Electric Fields The Electric















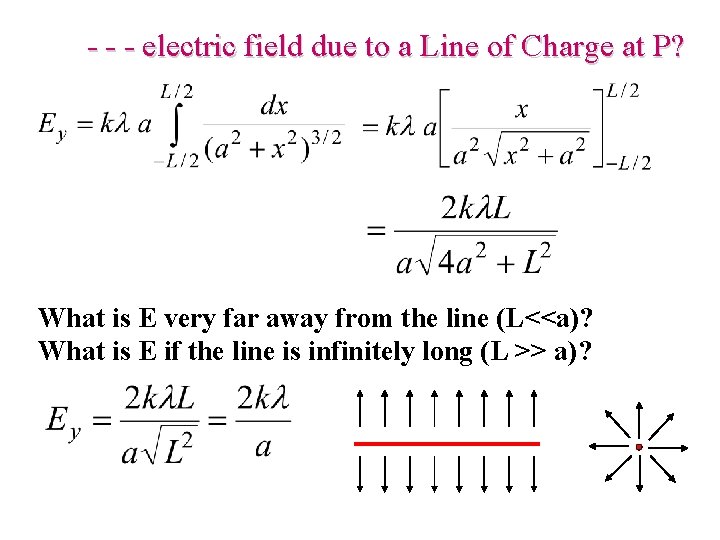








- Slides: 34

Physics 014 Chapter 22: Electric Fields

The Electric Field ? Q: How does particle 1 “know” of the presence of particle 2? That is, since the particles do not touch, how can particle 2 push on particle 1—how can there be such an action at a distance? Ans: particle 2 pushes on particle 1 not by touching it as you would push on a coffee mug by making contact. Instead, particle 2 pushes by means of the electric field it has set up.

Electric Field The electric field E at any point is defined in terms of the electrostatic force F that would be exerted on a positive test charge q 0 placed there: Since E is the force per unit charge, it is measured in units of N/C.

Electric Field Lines • The field lines of a positive charge radiate outward in all directions – In three dimensions, the distribution is spherical • The field lines of a negative charge radiate inward in all directions

Example 1. The isolated point charge of q=+15μC is in a vacuum. A test charge qo=+15μC is 0. 20 m to the right. Find the electric field at point p?

Electric Field Lines • Field lines: useful way to Example: a negative point visualize electric field E charge — note spherical symmetry • Field lines start at a positive charge, end at negative charge • E at any point in space is tangential to field line • Field lines are closer where E is stronger

Superposition • Question: How do we figure out the field due to several point charges? • Answer: consider one charge at a time, calculate the field (a vector!) produced by each charge, and then add all the vectors! (“superposition”) • Useful to look out for SYMMETRY to simplify calculations!

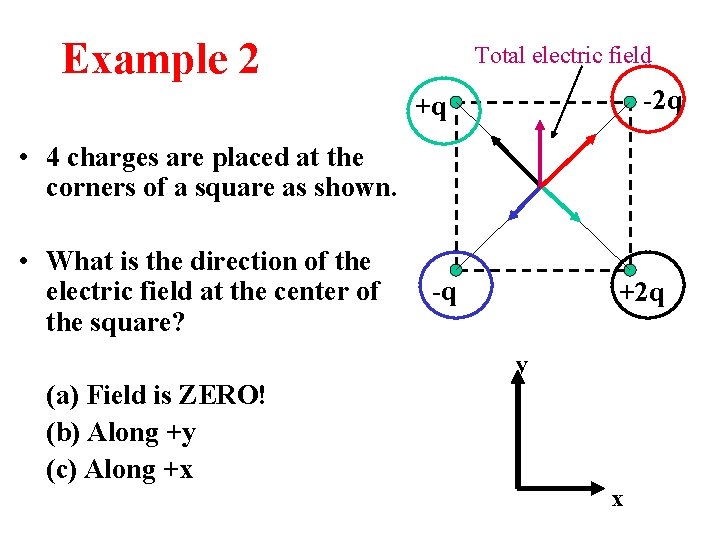
Example 2 Total electric field -2 q +q • 4 charges are placed at the corners of a square as shown. • What is the direction of the electric field at the center of the square? -q +2 q y (a) Field is ZERO! (b) Along +y (c) Along +x x

Electric Field of a Dipole • Electric dipole: two point charges +q and –q separated by a distance d • Common arrangement in Nature: molecules, antennae, … • Define “dipole moment” vector p: from –q to +q, with magnitude qd

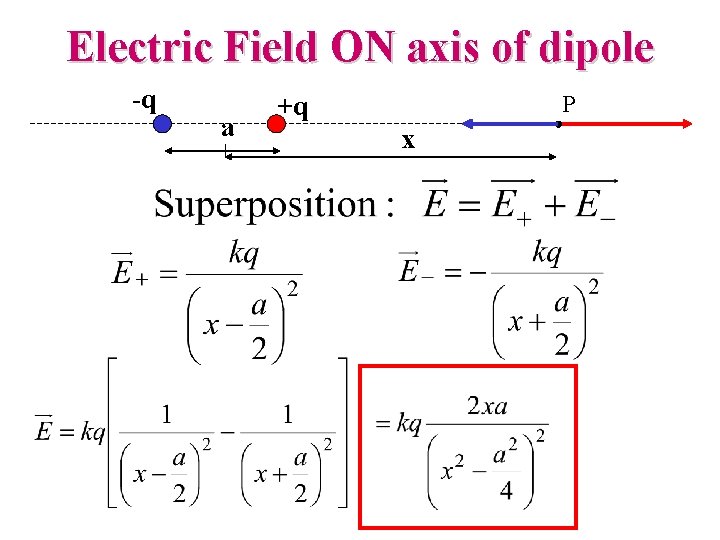
Electric Field ON axis of dipole -q a +q P x

Electric Field ON axis of dipole p = qa “dipole moment” -- VECTOR - + What if x>> a? (i. e. very far away) E~p/r 3 is actually true for ANY point far from a dipole (not just on axis)

Continuous Charge Distribution • Thus far, we have only dealt with discrete, point charges. • Imagine instead that a charge Q is smeared out over a: Q Q – LINE – AREA – VOLUME • How to compute the electric field E? ? Q Q

Electric Field – Continuous Charge Distribution, equations • For a single charge • For individual charge elements • For continuous charge distribution

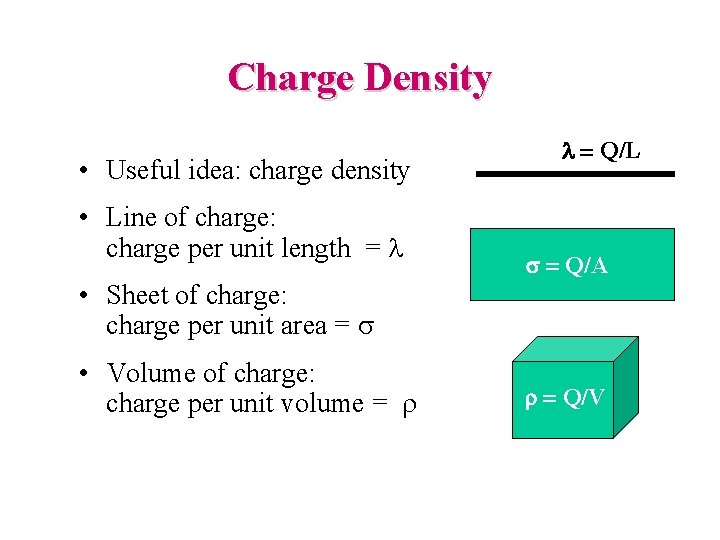
Charge Density • Useful idea: charge density • Line of charge: charge per unit length = l l = Q/L s = Q/A • Sheet of charge: charge per unit area = s • Volume of charge: charge per unit volume = r r = Q/V

Charge Density • Volume charge density: when a charge is distributed evenly throughout a volume ρ=Q/V with units C/m 3 • Surface charge density: when a charge is distributed evenly over a surface area σ =Q/A with units C/m 2 • Linear charge density: when a charge is distributed along a line λ = Q/ℓ with units C/m

Computing electric field of continuous charge distribution • Approach: divide the continuous charge distribution into infinitesimally small elements • Treat each element as a POINT charge & compute its electric field • Sum (integrate) over all elements • Always look for symmetry to simplify life!

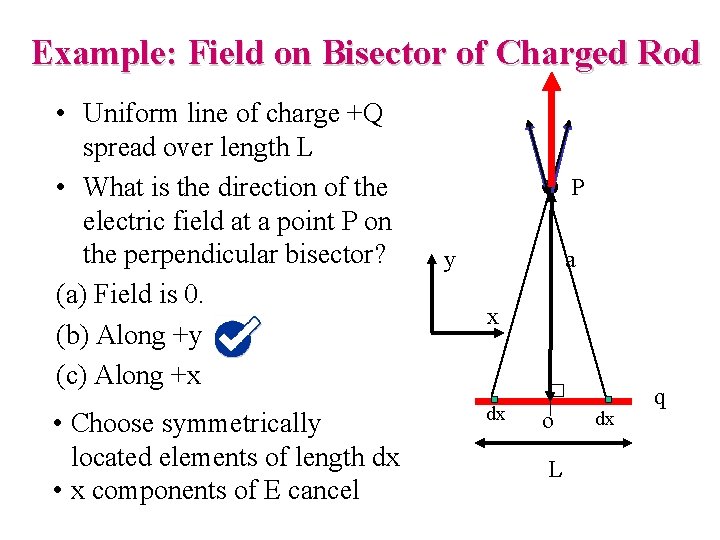
Example: Field on Bisector of Charged Rod • Uniform line of charge +Q spread over length L • What is the direction of the electric field at a point P on the perpendicular bisector? (a) Field is 0. (b) Along +y (c) Along +x • Choose symmetrically located elements of length dx • x components of E cancel P y a x dx o L dx q

Example 3: Find the electric field due to a Line of Charge at point P? • Uniform line of charge, length L, total charge Q • Compute explicitly the magnitude of E at point P on perpendicular bisector • Showed earlier that the net field at P is in the y direction -- let’s now compute this! P y a x o L Q

- - - electric field due to a Line of Charge at P? Distance d. E P Charge per unit length a d dx x o L Q
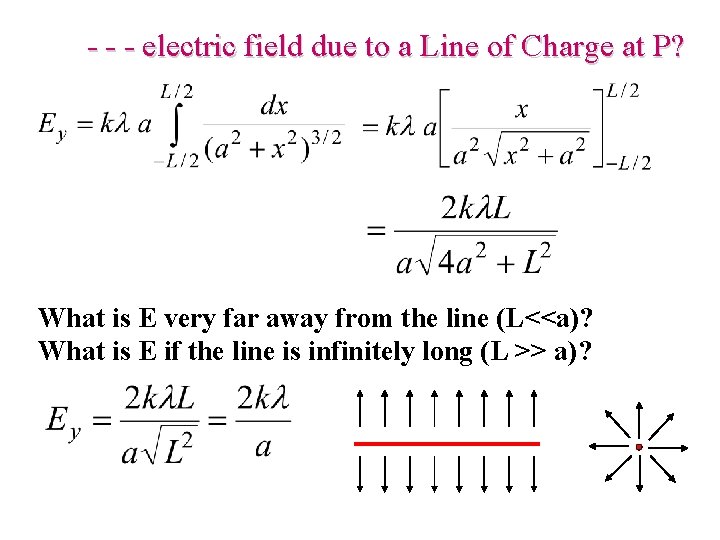
- - - electric field due to a Line of Charge at P? What is E very far away from the line (L<<a)? What is E if the line is infinitely long (L >> a)?

Problem-Solving Strategy • Conceptualize – Establish a mental representation of the problem – Image the electric field produced by the charges or charge distribution • Categorize – Individual charge? – Group of individual charges? – Continuous distribution of charges?

Problem-Solving Strategy, cont • Analyze – Units: when using the Coulomb constant, ke, the charges must be in C and the distances in m – Analyzing a group of individual charges: • Use the superposition principle, find the fields due to the individual charges at the point of interest and then add them as vectors to find the resultant field • Be careful with the manipulation of vector quantities – Analyzing a continuous charge distribution: • The vector sums for evaluating the total electric field at some point must be replaced with vector integrals • Divide the charge distribution into infinitesimal pieces, calculate the vector sum by integrating over the entire charge distribution

Problem Solving Hints, final • Analyze, cont. – Symmetry: • Take advantage of any symmetry to simplify calculations • Finalize – Check to see if the electric field expression is consistent with your mental representation – Check to see if the solution reflects any symmetry present – Image varying parameters to see if the mathematical result changes in a reasonable way

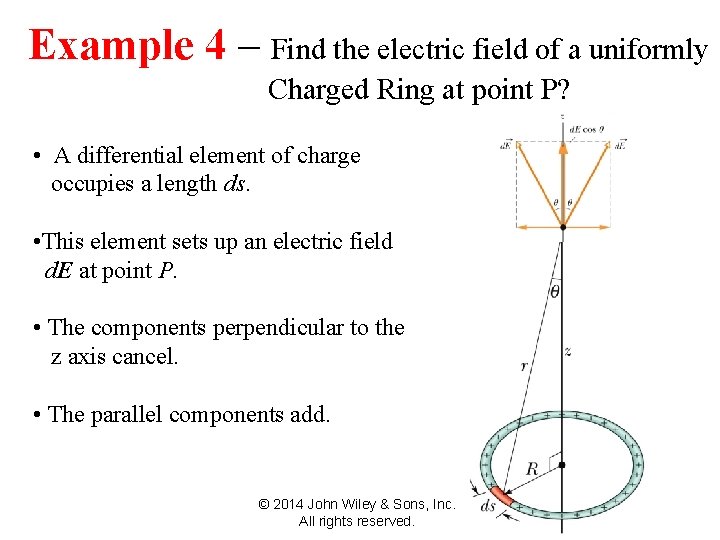
Example – Find the. Due electric fieldofof a uniformly 22 -4 The 4 Electric Field to a Line Charged Ring at point P? • A differential element of charge occupies a length ds. • This element sets up an electric field d. E at point P. • The components perpendicular to the z axis cancel. • The parallel components add. © 2014 John Wiley & Sons, Inc. All rights reserved.

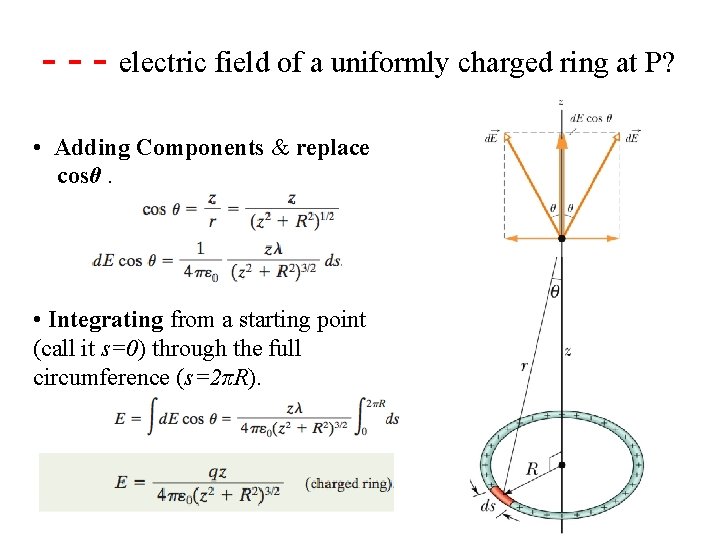
The Electric Due to a charged Line of Charge - - -22 -4 electric field of. Field a uniformly ring at P? • Adding Components & replace cosθ. • Integrating from a starting point (call it s=0) through the full circumference (s=2πR).

Example – Find. Field the Due electric field of Disk a uniformly 22 -5 The 5 Electric to a Charged Disc at point P? • We superimpose a ring on the disk as shown • The ring has radius r, radial width dr, and a charge element dq. • It sets up a differential electric field d. E at point P on its central axis. • Then, we can sum all the d. E contributions with • We find © 2014 John Wiley & Sons, Inc. All rights reserved.

A Point Charge ininan Field 22 -6 A Point Charge an. Electric Field If a particle with charge q is placed in an external electric field E, an electrostatic force F acts on the particle: Ink-jet printer. Drops shot from generator G receive a charge in charging unit C. An input signal from a computer controls the charge and thus the effect of field E on where the drop lands on the paper. © 2014 John Wiley & Sons, Inc. All rights reserved.

A Dipole in an Field 22 -7 A Dipole in an. Electric Field The torque on an electric dipole of dipole moment p when placed in an external electric field E is given by a cross product: A potential energy U is associated with the orientation of the dipole moment in the field, as given by a dot product: (a) An electric dipole in a uniform external electric field E. Two centers of equal but opposite charge are separated by distance d. The line between them represents their rigid connection. (b) Field E: causes a torque τ on the dipole. The direction of τ is into the page, as represented by the symbol (x-in a circle). © 2014 John Wiley & Sons, Inc. All rights reserved.

Summary 22 Summary Definition of Electric Field • The electric field at any point Eq. 22 -1 Electric Field Lines • provide a means for visualizing the directions and the magnitudes of electric fields Field due to a Point Charge • The magnitude of the electric field E set up by a point charge q at a distance r from the charge is Field due to an Electric Dipole • The magnitude of the electric field set up by the dipole at a distant point on the dipole axis is Eq. 22 -9 Field due to a Charged Disk • The electric field magnitude at a point on the central axis through a uniformly charged disk is given by Eq. 22 -3 © 2014 John Wiley & Sons, Inc. All rights reserved. Eq. 22 -26

22 Summary Force on a Point Charge in an Electric Field • When a point charge q is placed in an external electric field E Dipole in an Electric Field • The electric field exerts a torque on a dipole Eq. 22 -34 Eq. 22 -28 • The dipole has a potential energy U associated with its orientation in the field Eq. 22 -38 © 2014 John Wiley & Sons, Inc. All rights reserved.

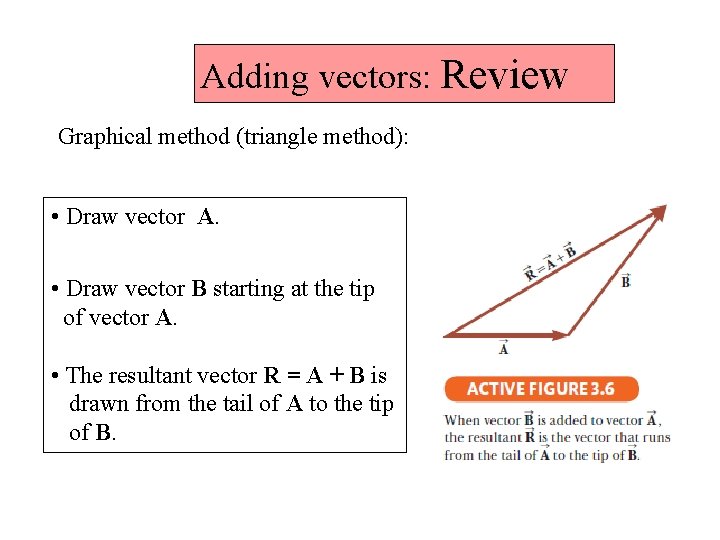
Adding vectors: Review Graphical method (triangle method): • Draw vector A. • Draw vector B starting at the tip of vector A. • The resultant vector R = A + B is drawn from the tail of A to the tip of B.

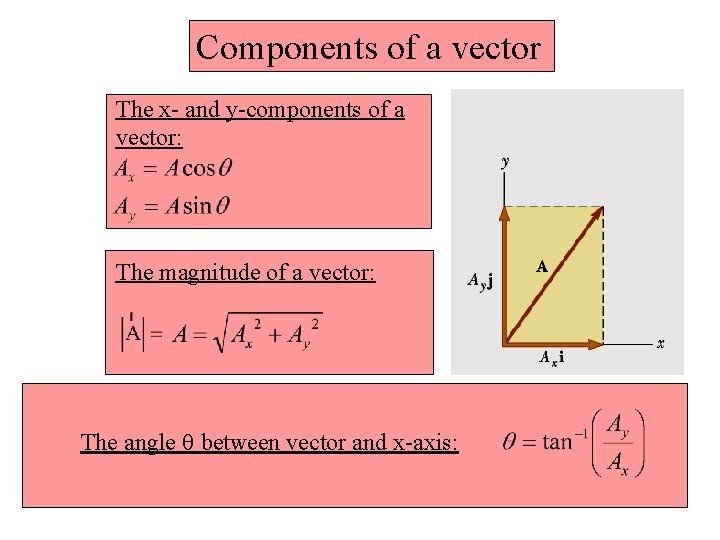
Components of a vector The x- and y-components of a vector: The magnitude of a vector: The angle q between vector and x-axis:

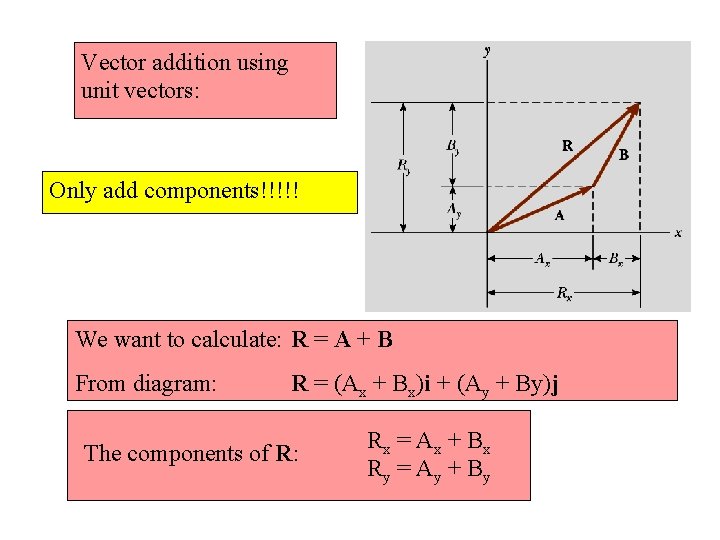
Vector addition using unit vectors: Only add components!!!!! We want to calculate: R = A + B From diagram: R = (Ax + Bx)i + (Ay + By)j The components of R: Rx = Ax + B x Ry = Ay + B y

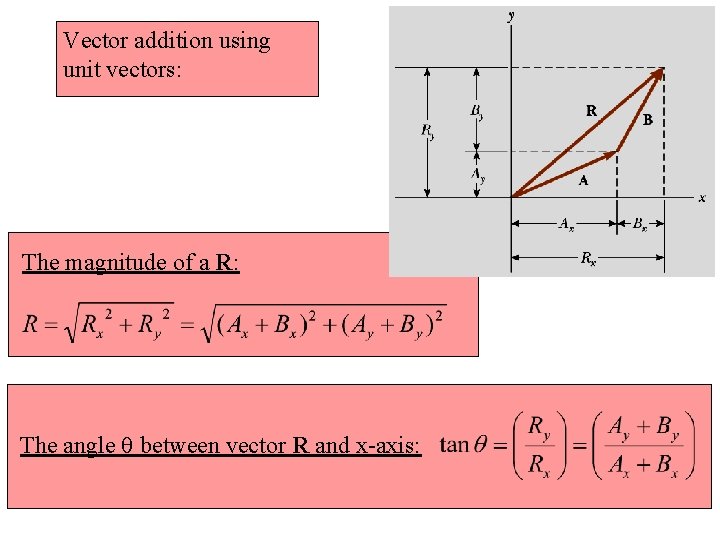
Vector addition using unit vectors: The magnitude of a R: The angle q between vector R and x-axis: