Electrostatics Coulombs Law Coulombs Law F kq 1

Electrostatics Coulomb’s Law

Coulomb’s Law F = (kq 1 q 2)/r 2 K = 9 x 109 Nm 2/C 2 Positive force means repulsion Negative force means attraction

Example problem A charge q 1 = 4 μC is positioned at the origin. A charge of q 2 = 9 μC is positioned at x = 4 m. Where on the xaxis can a charge q 3 be placed so that the force is zero? 4 m q 1 q 3 q 2

Solution (kq 1 q 3)/x 2 = (kq 2 q 3)/ (4 -x)2 kq 1(4 -x)2 = kq 2 x 2 4 μC (4 -x)2 = 9 x 2 4(16 -8 x+x 2) = 9 x 2 5 x 2 +32 x – 64 = 0 x = 1. 6 m

Example problem Table salt is a crystal with a simple cubic structure with Na+ and Cl- ions alternating on adjacent lattice sites. The distance between ions is a = 2. 82 x 10 -10 m. a)What force does Na+ experience due to one of its Clneighbors? B)What force does a Cl- ion experience due to a neighboring Na+? c)What force does an Na+ ion at the origin experience due to Cl- ions at (a, 0, 0) and (0, a, 0)?

Solution A) F = kq 1 q 2/r 2 = [9 x 109 (1. 6 x 10 -19 C)2]/(. 282 x 10 -10 m)2 = 2. 9 x 10 -9 N B) same as a by Newton’s Third Law C) F = F 1 + F 2 = 2. 9 x 10 -9 (i + j) N = √(2. 9 x 10 -9)2 + (2. 9 x 10 -9 )2 = 4. 1 x 10 -9 N

Electric Field Vector Quantity At every point in space it has a magnitude and direction The total electric field at any point is the sum of the electric fields due to all charges that are present Unit: N/C Always point away from positive charge and toward negative charge

Problem Find the force on a Ca+2 ion placed in an electric field of 800 N/C directed along the positive z-axis. Solution: F = q. E q = 2 e F = 2 e(800 N/C) 2. 56 x 10 -16 N

Electric Field E = F/q F = kq. Q/r 2 E = kq. Q/qr 2 E = k. Q/r 2

Problem 2 A point charge q = -8. 0 n. C is located at the origin. Find the electric field vector at the field point x = 1. 2 m and y = -1. 6 m.

Solution E = - 11 N/C i and 14 N/C j
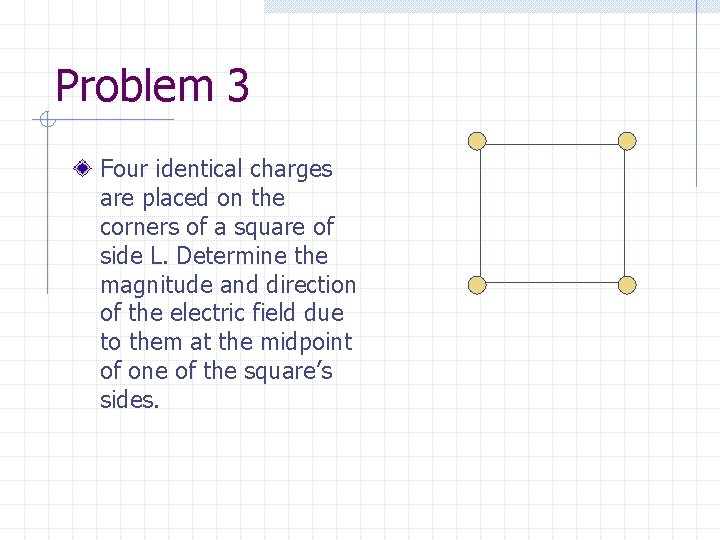
Problem 3 Four identical charges are placed on the corners of a square of side L. Determine the magnitude and direction of the electric field due to them at the midpoint of one of the square’s sides.
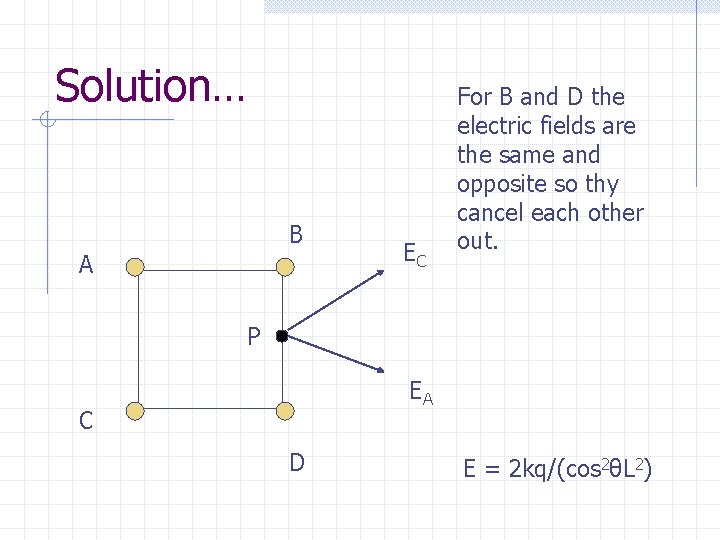
Solution… B A EC For B and D the electric fields are the same and opposite so thy cancel each other out. P EA C D E = 2 kq/(cos 2θL 2)

Problem 4 An electric dipole consists of +q and –q and separated by a distance of 2 a. If the charges are positioned at (0, 0, a and (0, 0, -a) determine the electric field at a point a distance of z from the origin on the z-axis, where z >> 2 a.

Charge Distributions and Efields ΔE = k ΔQ/r 2 r E = k Σi Δqi/ri 2 r E = k lim Σ Δqi/ri 2 r = k ∫dq/r 2 r

Linear charge distribution Charge Q is distributed on a line of length l, the linear charge density λ = Q/l dq = λ dl

Surface Area Charge Distribution Charge Q is distributed on a surface area A, the surface density δ = Q/A dq = δ dl

Volume Charge Distribution Charge Q is distributed uniformly throughout a volume V, the volume charge density ρ = Q/V dq = ρ dl

Problem 1 A rod of length l has a uniform positive charge per unit length, λ, and a total charge, Q. Calculate the electric field at a point P along the axis of the rod and a distance a from one end.

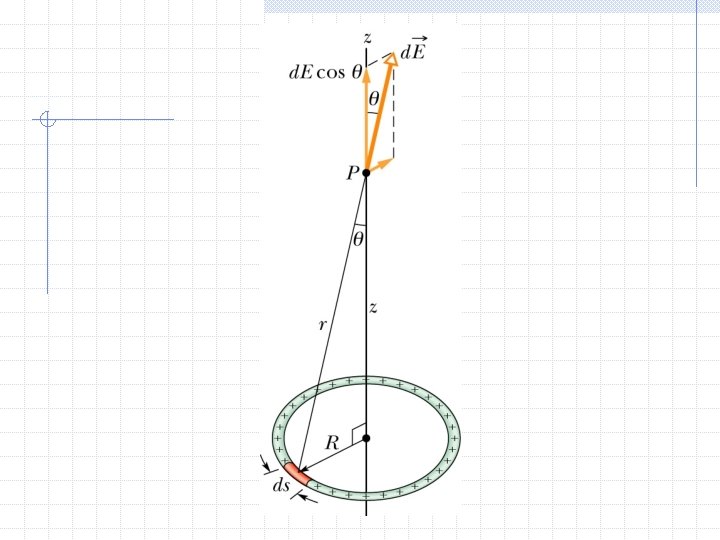
Problem 2 A ring of radius a carries a uniformly distributed positive charge Q. Calculate the E field due to the ring at a point P lying a distance x from its center along the central axis perpendicular to the plane of the ring.
- Slides: 21