Chapter 24 Gausss Law Electric Flux Electric flux

Chapter 24 Gauss’s Law

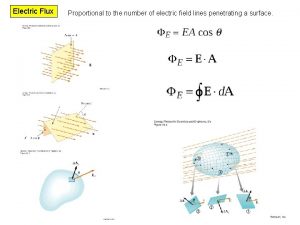
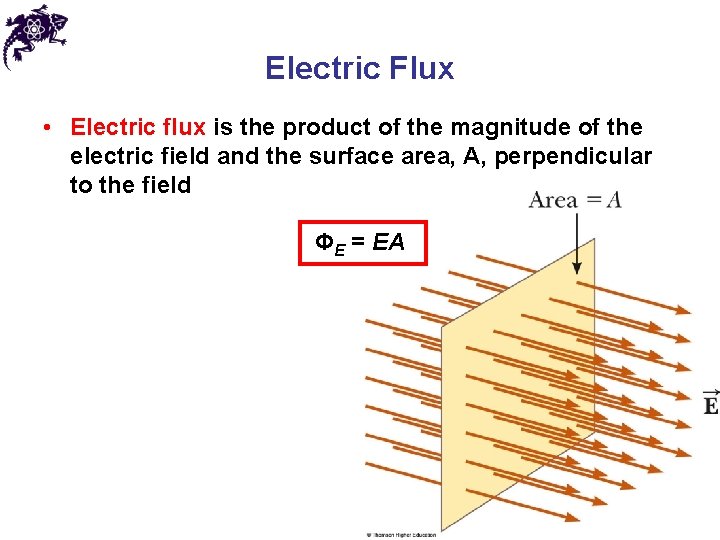
Electric Flux • Electric flux is the product of the magnitude of the electric field and the surface area, A, perpendicular to the field ΦE = EA

Electric Flux • The electric flux is proportional to the number of electric field lines penetrating some surface • The field lines may make some angle θ with the perpendicular to the surface • Then ΦE = EA cos θ • The flux is a maximum (zero) when the surface is perpendicular (parallel) to the field

Electric Flux • If the field varies over the surface, Φ = EA cos θ is valid for only a small element of the area • In the more general case, look at a small area element • In general, this becomes

Electric Flux • The surface integral means the integral must be evaluated over the surface in question • The value of the flux depends both on the field pattern and on the surface • SI units: N. m 2/C

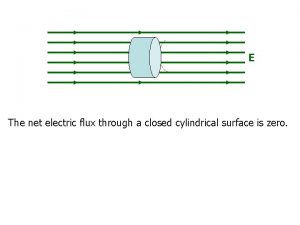
Electric Flux, Closed Surface • For a closed surface, by convention, the A vectors are perpendicular to the surface at each point and point outward • (1) θ < 90 o, Φ > 0 • (2) θ = 90 o, Φ = 0 • (3) 180 o > θ > 90 o, Φ < 0

Electric Flux, Closed Surface • The net flux through the surface is proportional to the number of lines leaving the surface minus the number entering the surface

Electric Flux, Closed Surface • Example: flux through a cube • The field lines pass perpendicularly through two surfaces and are parallel to the other four surfaces • Side 1: Φ = – E l 2 • Side 2: Φ = E l 2 • For the other sides, Φ = 0 • Therefore, Φtotal = 0

Chapter 24 Problem 5 A pyramid with horizontal square base, 6. 00 m on each side, and a height of 4. 00 m is placed in a vertical electric field of 52. 0 N/C. Calculate the total electric flux through the pyramid’s four slanted surfaces.

Gauss’ Law Carl Friedrich Gauss 1777 – 1855 • Gauss’ Law: electric flux through any closed surface is proportional to the net charge Q inside the surface • εo = 8. 85 x 10 -12 C 2/Nm 2 : permittivity of free space • The area in Φ is an imaginary Gaussian surface (does not have to coincide with the surface of a physical object)

Gauss’ Law • A positive point charge q is located at the center of a sphere of radius r • The magnitude of the electric field everywhere on the surface of the sphere is E = keq / r 2 • Asphere = 4πr 2

Gauss’ Law • Gaussian surfaces of various shapes can surround the charge (only S 1 is spherical) • The electric flux is proportional to the number of electric field lines penetrating these surfaces, and this number is the same • Thus the net flux through any closed surface surrounding a point charge q is given by q/eo and is independent of the shape of the surface

Gauss’ Law • If the charge is outside the closed surface of an arbitrary shape, then any field line entering the surface leaves at another point • Thus the electric flux through a closed surface that surrounds no charge is zero

Gauss’ Law • Since the electric field due to many charges is the vector sum of the electric fields produced by the individual charges, the flux through any closed surface can be expressed as • Although Gauss’s law can, in theory, be solved to find for any charge configuration, in practice it is limited to symmetric situations • One should choose a Gaussian surface over which the surface integral can be simplified and the electric field determined

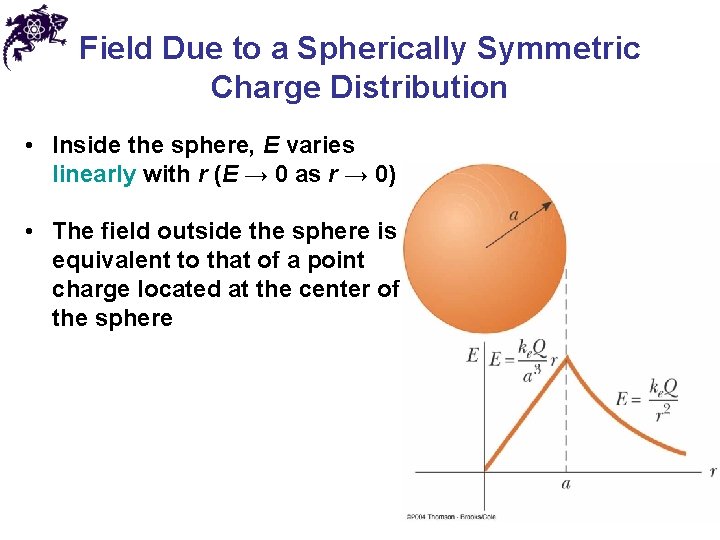
Field Due to a Spherically Symmetric Charge Distribution • For r > a • For r < a

Field Due to a Spherically Symmetric Charge Distribution • Inside the sphere, E varies linearly with r (E → 0 as r → 0) • The field outside the sphere is equivalent to that of a point charge located at the center of the sphere

Chapter 24 Problem 18 A solid sphere of radius 40. 0 cm has a total positive charge of 26. 0 1μC uniformly distributed throughout its volume. Calculate the magnitude of the electric field (a) 0 cm, (b) 10. 0 cm, (c) 40. 0 cm, and (d) 60. 0 cm from the center of the sphere.

Electric Field of a Charged Thin Spherical Shell • The calculation of the field outside the shell is identical to that of a point charge • The electric field inside the shell is zero

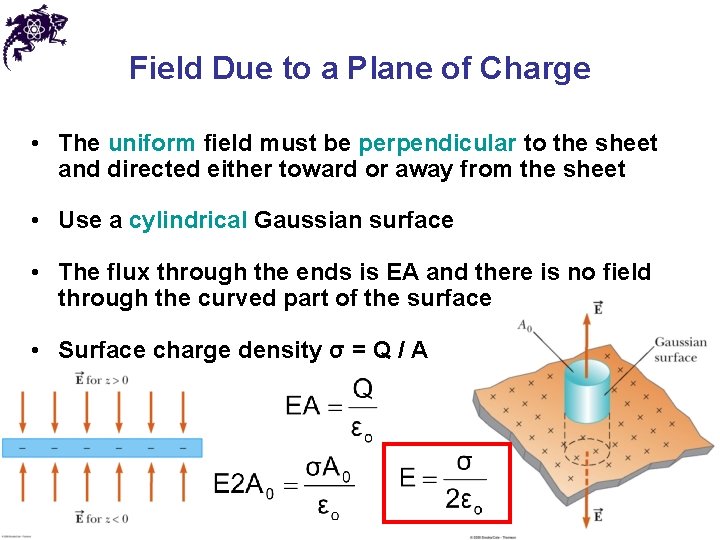
Field Due to a Plane of Charge • The uniform field must be perpendicular to the sheet and directed either toward or away from the sheet • Use a cylindrical Gaussian surface • The flux through the ends is EA and there is no field through the curved part of the surface • Surface charge density σ = Q / A

Conductors in Electrostatic Equilibrium • When no net motion of charge occurs within a conductor, the conductor is said to be in electrostatic equilibrium • An isolated conductor has the following properties: • Property 1: The electric field is zero everywhere inside the conducting material • If this were not true there were an electric field inside the conductor, the free charge there would move and there would be a flow of charge – the conductor would not be in equilibrium

Conductors in Electrostatic Equilibrium • When no net motion of charge occurs within a conductor, the conductor is said to be in electrostatic equilibrium • An isolated conductor has the following properties: • Property 2: Any excess charge on an isolated conductor resides entirely on its surface • The electric field (and thus the flux) inside is zero whereas the Gaussian surface can be as close to the actual surface as desired, thus there can be no charge inside the surface and any net charge must reside on the surface

Conductors in Electrostatic Equilibrium • When no net motion of charge occurs within a conductor, the conductor is said to be in electrostatic equilibrium • An isolated conductor has the following properties: • Property 3: The electric field just outside a charged conductor is perpendicular to the surface and has a magnitude of σ/εo • If this was not true, the component along the surface would cause the charge to move – no equilibrium

Conductors in Electrostatic Equilibrium • When no net motion of charge occurs within a conductor, the conductor is said to be in electrostatic equilibrium • An isolated conductor has the following properties: • Property 4: On an irregularly shaped conductor, the charge accumulates at locations where the radius of curvature of the surface is smallest • Proof – see Chapter 25

Answers to Even Numbered Problems Chapter 24: Problem 64 For r < a: /2 0 r; radially outward. For a < r < b: [ + (r 2 a 2)]/2 0 r; radially outward. For r > b: [ + (b 2 a 2)]/2 0 r; radially outward.