Field Definition And Coulombs Law Coulombs Law Gives

Field Definition And Coulomb’s Law

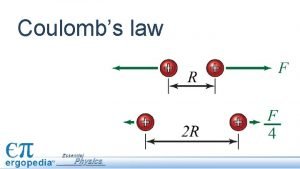
Coulomb’s Law • Gives us the rule for dealing with two point charges. (in practice for two charges whose separation is much greater than the radius of the charges. ) r Charge Q 1 Charge Q 2

The field strength of an electric field is defined by (Unit NC-1) That is the force exerted by the field on unit charge (ie a charge of 1 Coulomb) placed at that point. +1 C F
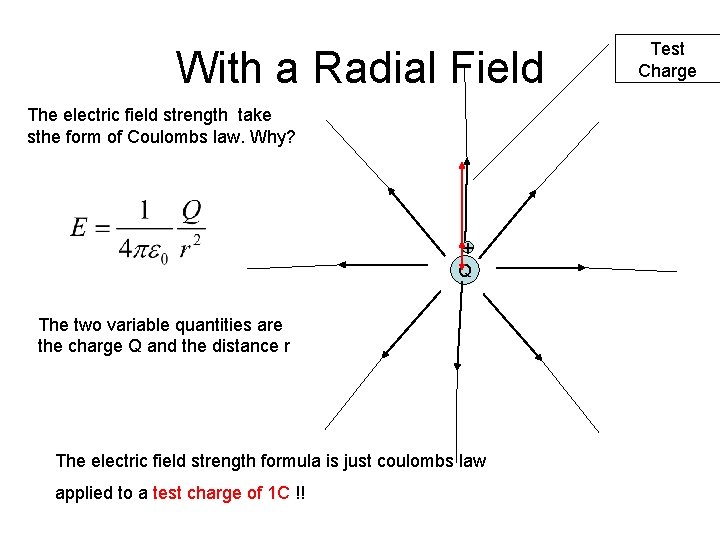
With a Radial Field The electric field strength take sthe form of Coulombs law. Why? + Q The two variable quantities are the charge Q and the distance r The electric field strength formula is just coulombs law applied to a test charge of 1 C !! Test Charge
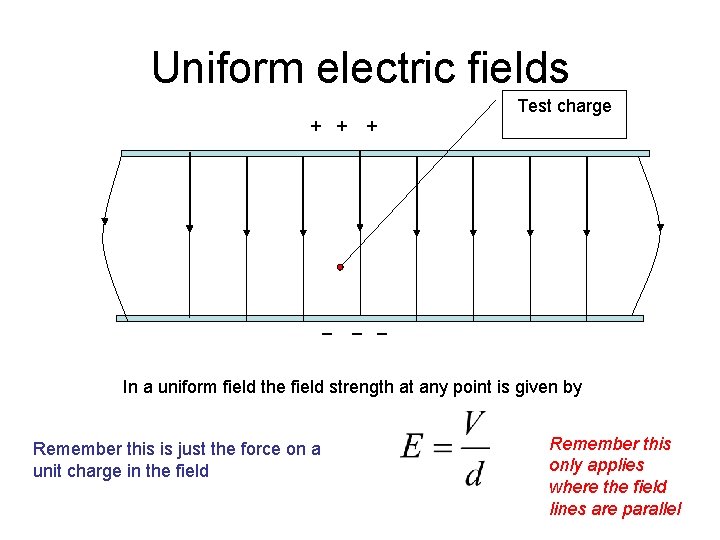
Uniform electric fields Test charge + + + _ _ _ In a uniform field the field strength at any point is given by Remember this is just the force on a unit charge in the field Remember this only applies where the field lines are parallel

Together with these relationships: The definition of the volt The electric field strength due to a point charge The electric field strength in a uniform field So the unit of E is Vm-1 as well as NC-1 Form the basis of any solution to the electric fields questions you will be asked
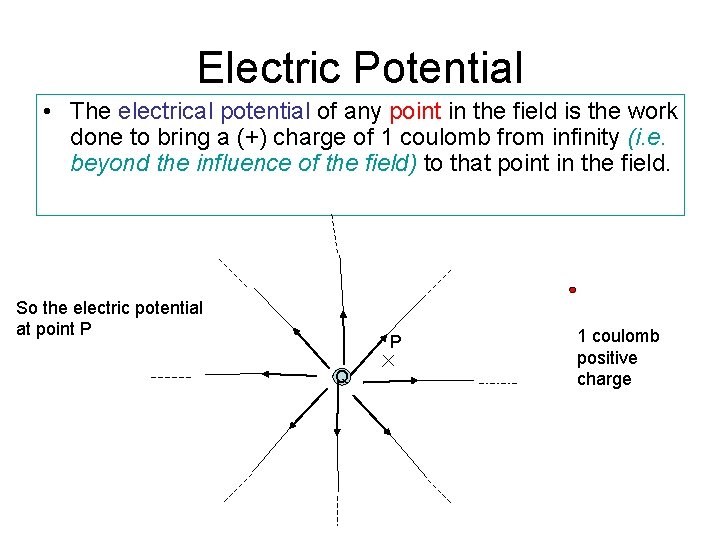
Electric Potential • The electrical potential of any point in the field is the work done to bring a (+) charge of 1 coulomb from infinity (i. e. beyond the influence of the field) to that point in the field. So the electric potential at point P P Q 1 coulomb positive charge

Implications: 1. The electrical potential of any point beyond the field is zero 2. The electric potential is the potential energy change for 1 C of charge The electric potentila is given by:

Calculations 4. 0μC -6. 0μC A B Two charges with the values shown are placed along are separated 100 mm from A along the line AB by a distance of 100 mm. At what distance does the electric potential reach 0 V? When the potential along AB reaches zero VA=VB i. e. Now: VA +VB = 0

V=0 4. 0μC 40 mm 60 mm A -6. 0μC B 100 mm This ratio tells us that V=0 40 mm from A

Where the numbers are not as straightforward you can continue as follows: 1 As the total distance between the charges is 100 mm 2 Now substituting 2 into 1

Calculate the magnitude of the electric field strength at the surface of a nucleus U (Z=92 M=238). Assume that the radius of this nucleus is 7. 4 × 10– 15 m. . . . . . . . . . . . . . . . . . . . . . . . . Magnitude of electric field strength =. . . . . State the direction of this electric field. . . . . . . . . State one similarity and one difference between the electric field and the gravitational field produced by the nucleus. Similarity. . . . . . . . . . . . . . . . Difference. . . . . . . . . . . . . . . .

The diagram shows a positively charged oil drop held at rest between two parallel conducting plates A and B. The oil drop has a mass 9. 79 x 10– 15 kg. The potential difference between the plates is 5000 V and plate B is at a potential of 0 V. Is plate A positive or negative? ……………………………………………… Calculate the electric field strength between the plates. Electric field strength =………………… Calculate the magnitude of the charge Q on the oil drop. Charge =………………… How many electrons would have to be removed from a neutral oil drop for it to acquire this charge? ……………………………………………… (3)
- Slides: 13