Electrostatics Electric charge Van de Graff generators Conservation




































- Slides: 36

Electrostatics § Electric charge § Van de Graff generators § Conservation of charge § Equilibrium problems § Insulators & conductors § Grounding § Charging objects § Static electricity § Electroscopes § Coulomb’s law § Lightning § Systems of charges

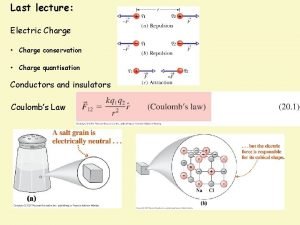
Electric Charge • Just as most particles have an attribute known as mass, many possess another attribute called charge. Charge and mass are intrinsic properties, defining properties that particles possess by their very nature. • Unlike mass, there are two different kinds of charge: positive and negative. • Particles with a unlike charges attract, while those with like charges repel. • Most everyday objects are comprised of billions of charged, but usually there about the same number of positive charges as negative, leaving the object as a whole neutral. • A charged object is an object that has an excess of one type of charge, e. g. , more positive than negative. The amount of excess charge is the charge we assign to that object.

Conservation of Charged particles can be transferred from one object to another, but the total amount of charge is conserved. Experiments have shown that whenever subatomic particles are transferred between objects or interact to produce other subatomic particles, the total charge before and after is the same (along with the total energy and momentum). Example: An object with 5 excess units of positive charge and another with 2 units of excess negative charge are released from rest and attract each other. (By Newton’s 3 rd law, the forces are equal strength, opposite directions, but their accelerations depend on their masses too. ) Since there is no net force on the system, their center of mass does not accelerate, and they collide there. As they “fall” toward each other, electric potential energy is converted to kinetic energy. When contact is made charge may be exchanged but they total amount before and after must be the same. After the collision the total momentum must still be zero. Before +5 After -2 Total charge: +3 +1. 5 Total charge: +3

Conservation of Charge: β-decay • The stability of the nucleus of an atom depends on its size and its proton-neutron ratio. This instability sometimes results in a radioactive process known as β-decay. • A neutron can turn into a proton, but in the process an electron (beta particle) is ejected at high speed from the nucleus to conserve charge. • A proton can turn into a neutron. In this case the beta particle is an positron (an antielectron: same mass as an electron but a positive charge) to make up for the loss of positive charge of the proton. • In either case, charge, momentum, and energy are conserved.

SI unit of Charge: the Coulomb • Just as we have an SI unit for mass, the kilogram, we have one for charge as well. It’s called the coulomb, and its symbol is C. • It’s named after a French physicist, Charles Coulomb, who did research on charges in the mid and late 1700’s. • A coulomb is a fairly large amount of charge, so sometimes we measure small amounts of charge in μC (mircocoloumbs). • An electron has a charge of -1. 6 10 -19 C. • A proton has a charge of +1. 6 10 -19 C. • In a wire, if one coulomb of charge flows past a point in one second, we say the current in the wire is one ampere.

Elementary Charge • Charges come in small, discrete bundles. Another way to say this is that charge is quantized. This means an object can possess charge in incremental, rather than continuous, amounts. • Imagine the graph of a linear function buy when you zoom in very close you see that it really is a step function with very small steps. • The smallest amount of charge that can be added or removed from an object is the elementary charge, e = 1. 6 10 -19 C. • The charge of a proton is +e, an electron -e. • The charge of an object, Q, is always a multiple of this elementary charge: Q = N e, where N is an integer. • How many excess protons are required for an object to have 1 C of charge?

Insulators vs. Conductors • A conductor is a material in which excess charge freely flows. Metals are typically excellent conductors because the valence (outer shell) electrons in metal atoms are not confined to any one atom. Rather, they roam freely about a metal object. Metal are excellent conductors of electricity (and heat) for this reason. • An insulator is a material in which excess charge, for the most part, resides where it is deposited. That is, once placed, it does not move. Most nonmetallic material are good insulators. Valence electrons are much more tightly bound to the atoms and are not free to roam about. Insulators are useful for studying electrostatics (the study of charge that can be localized and contained). • Semi-conductors, like silicon used in computer chips, have electrical conductivity between that of conductors and insulators. Details on Conductors, Semiconductors, and Insulators

Electrons and Chemical Bonds All chemical bonding is due to forces between electrostatic charges. Covalent bonding: A pair of electrons is shared between two nonmetal atoms, allowing each atom to have access to enough electrons to fill its outer shell. Except for hydrogen, this usually means 8 electrons in the outer shell (octet rule). Ionic bonding: One or more valence electrons of a metal atom are “stolen” by a nonmetal atom, leaving a positive metal ion and a negative nonmetal ion, which then attract one another. Metallic bonding: Valence electrons of metals flow freely throughout a metal object. These delocalized electrons are attracted to the nuclei of the atoms through which they are moving about. This produces a strong binding force that holds the atoms together. In an iron bar, for example, there is no covalent or ionic bonding. Metallic bonding hold the metal together.

Charging up Objects Charging up an object does not mean creating new charges. Charging implies either adding electrons to an object, removing electrons from an object, or separating out positive and negative charges within an object. This can be accomplish in 3 different ways: • Friction: Rubbing two materials together can rub electrons off of one and onto the other. • Conduction: Touching an object to a charged object could lead to a flow of charge between them. • Induction: If a charged object is brought near (but not touching) a second object, the charged object could attract or repel electrons (depending on its charge) in the second object. This yields a separation charge in the second object, an induced charge separation.

Electroscopes An electroscope is an apparatus comprised of a metal sphere and very light metal leaves. A metal rod connects the leaves to the sphere. The leaves are enclosed in an insulating, transparent container. When the electroscope is uncharged the leaves hang vertically. The scope is charged by placing a charged rod near the sphere. The rod is charged by friction. If a rubber rod is rubbed with fur, electrons will be rubbed off the fur and onto the rubber rod, leaving the rod negatively charged. If a glass rod is rubbed with silk, electrons will be rubbed off the rod onto the silk, leaving the glass rod positively charged. Either rod, if brought near, will charge the scope by induction. Also, either rod, if contact is made with the sphere, will charge the scope by conduction. Electroscopes uncharged continued…

Electroscopes (cont. ) When a positively charged rod is placed near but not touching the metal sphere, some of the valence electrons in the metal leaves are drawn up into the sphere, leaving the sphere negatively charged and the leaves positively charged. Thus, the rod has induced a charge separation in the scope. The light, +++++++ positive leaves repel each other and separate. The electroscope as a whole -- - -is still electrically neutral, but it has -undergone a charge separation. As soon as the rod is removed from the vicinity, the charge separation will + + cease to exist and the leaves the drop. Note: Only the electron are mobile; + + the positives on the leaves represent + + missing electrons. continued…

Electroscopes (cont. ) When a negatively charged rod is placed near but not touching the metal sphere, some of the valence electrons in the sphere are repelled down into the metal leaves, leaving the sphere positively charged and the leaves negatively charged. The rod has again induced a charge separation in the scope. The light, ---------negative leaves repel each other as before. Again, the electroscope as a ++ whole is electrically neutral, but the + + ++ charge separation will remain so long as the rod remains nearby. Note that this situation is indistinguishable from the situation with the positive rod. Since the effects are the same, how do we know that the rods really do have different charges? continued…

Electroscopes (cont. ) Now let’s touch the negative rod to the sphere. Some of the electrons can actually hop onto the sphere and spread throughout the scope. This is charging by conduction since, instead of rearranging charges in the scope, new charges have been added; the scope is no longer neutral. The extra electrons force the leaves apart, even when the rod is removed. If the negative rod returns, it charges the leaves further, but this time by induction (by driving some of --------electrons on the sphere down to - - - the leaves). This causes an - - increased separation of the leaves. When the rod is removed, the scope will return to the state on the left. Continued… extra e- ’s added leaf spread increases

Electroscopes (cont. ) The pic on the left shows a scope that has acquired extra electrons from a negative rod that has since been removed. Now we bring a positive rod nearby. This has the opposite effect of bringing the negative rod near. This time some of the extra electrons in the leaves head to the sphere and the spread of the leaves diminishes. Note: the scope is still negatively charged overall, but the presence of the positive rod means more of the ++++++ excess negative charge will - - - reside in the sphere and less in - - the leaves. When the rod is removed, the scope return to the state on the left. Continued… extra e- ’s added leaf spread decreases

Grounding an Electroscope Whether a scope has charged by conduction, either positively or negatively, the quickest way to “uncharge” it is by grounding it. To do this we simply touch the sphere. When a negatively charged scope is grounded by your hand, the excess electrons from the scope travel into your body and, from there, into your surroundings. When a positively charged scope is grounded, electrons from your body flow into the scope until ++ - it is neutral. Your surroundings - + + ++ - will replace the electrons you’ve donated to the scope. As always, it’s only the + + electrons that move around. + +

Electroscope Practice Problem For the following scenario, try to predict what would happen after each step. Explain each in terms of electrons and charging. 1. A rod is rubbed with a material that has a greater affinity for electrons than the rod does. 2. This rod is brought near a neutral electroscope. 3. This rod touches the electroscope and is removed. 4. A positive rod is alternately brought near and removed. 5. A negative rod is alternately brought near and removed. 6. Finally, you touch the scope with your finger.

Redistributing Charge on Conducting Spheres Two neutral spheres, A & B, are placed side by side, touching. A negatively charged rod is brought near A, which induces a charge separation in the “A-B system. ” Some of the valence e-’s in A migrate to B. When the rod is removed and A & B are separated, A is +, B is -, but the system is still neutral. --- +Q A B -Q B A A is now brought near neutral sphere C, inducing a charge separation on it. Valence e-’s in C migrate toward A, but since C is being touched on the positive side, e-’s from the hand will move into C. Interestingly, C retains a net negative charge after A and the hand are removed even though no charged object ever made contact with it. - +Q A C C

Static Electricity: Shocks If you walk around on carpeting in your stocking feet, especially in the winter when the air is dry, and then touch something metal, you may feel a shock. As you walk you can become negatively charged by friction. When you make contact with a metal door knob, you discharge rapidly into the metal and feel a shock at the point of contact. A similar effect occurs in the winter when you exit a car: if you slide out of your seat and touch then touch the car door, you might feel a shock. The reason the effect most often occurs in winter is because the air is typically drier then. Humidity in the air can rather quickly rob excess charges from a charged body, thereby neutralizing it before a rapid, localized discharge (and resulting shock) can take place. Care must be taken to prevent static discharges where sensitive electronics are in use or where volatile substances are stored.

+- # 1 +++++++-+ -+ - -+ - +++++- #3 Static Electricity: Balloons Pic #1: If you rub a balloon on your hair, electrons will be rubbed off your hair onto the balloon (charging by friction). #2 Pic #2: If you then place the negatively charged balloon near a neutral wall, the balloon will repel some of the electrons near it in the wall. This is inducing a charge separation in the wall. Now the wall, while still neutral, has a positive charge near the balloon. Thus, the balloon sticks to the wall. Pick #3: Your hair now might stand up. This is because it has been left positively charged. As with the leaves of a charged electroscope, the light hairs repel each other.

Hanging Balloons #1 You hang two balloons from the ceiling and rub them on your hair. #2 When you move out of the way, the negatively charged balloons repel each other. On each balloon there are three forces: tension in the string, gravity, and the electric force. The angle of separation will grow until equilibrium is achieved (zero net force). #3 If you move your head close to either of the balloons, it will move toward you since your hair remains positively charged.

Polarization of a Cloud Lightning is the discharge of static electricity on a massive scale. Before a strike the bottom part of a cloud becomes negatively charged and the top part positively charged. The exact mechanism by which this polarization (charge separation) takes place is uncertain, but this is the precursor to a lightning strike from cloud to cloud or cloud to ground. One mechanism incorporates friction: when moist, warm air rises, it cools and water droplets form. These droplets collide with ice crystals and water droplets in a cloud. Electrons are torn off the rising water droplets by the ice crystals. The positive droplets rise to the top of the cloud, while the negative ice crystals remain at the bottom. A second mechanism involves the freezing process: experiments have shown that when water vapor freezes the central ice crystal becomes negatively charged, while the water surrounding it becomes positive. If rising air tears the surrounding water from the ice, the cloud becomes polarized. There are other theories as well. Detailed Lightning Diagrams

Lightning Strikes The negative bottom part of the cloud induces a charge separation in the ground below. Air is normally a very good insulator, but if the charge separation is big enough, the air between the cloud and ground can become ionized (a plasma). This allows some of the electrons in the cloud to begin to migrate into the ionized air below. This is called a “leader. ” Positive ions from the ground migrate up to meet the leader. This is called a “streamer. ” As soon as the leader and streamer meet, a fully conductive path exists between the cloud and ground a lightning strike occurs. Billions of trillions of electrons flow into the ground in less than a millisecond. The strike can be hotter than the surface of the sun. The heat expands the surrounding air; which then claps as thunder. + +++ + + - -- - - + + + + +

Lightning Rods and Grounding Discovered by Ben Franklin, a lightning rod is a long, pointed, metal pole attached to a building. It may seem crazy to attract lightning close to a susceptible structure, but a lightning rod can afford some protection. When positive charges accumulate beneath a cloud, the accumulation is extremely high near the tip of the rod. As a result, an electric field is produced that is much greater surrounding the tip than around the building. (We’ll study electric fields in the next unit. ) This strong electric field ionizes the air around the tip of the rod and “encourages” a strike to occur there. If a strike does occur, the electricity travels down the rod into a copper cable that connects the lightning rod to a grounding rod buried in the earth. There the excess charge is grounded, i. e. , the electrons are dissipated throughout the landscape. By taking this route, rather than through a building and its wiring, much loss is prevented.

Van de Graaff Generator A Van de Graaff generator consists of a large metal dome attached to a tube, within which a long rubber belt is turning on rollers. As the belt turns friction between it and the bottom roller cause the e-’s to move from the belt to the roller. A metal brush then drains these e-’s away and grounds them. So, as the belt passes the bottom roller it acquires a positive charge, which is transported to the top of the device (inside the dome). Here another metal brush facilitates the transfer of electrons from the dome to the belt, leaving the dome positively charged. In short, the belt transports electrons from a metal dome to the ground, producing a very positively charged dome. No outside source of charge is required, and the generator could even be powered by a hand crank. A person touching the dome will have some of her e-’s drained out. So, her lightweight, positive hair will repel itself. Coming close to the charge dome will produce sparks when electrons jump from a person to the dome. Internal workings Detailed explanation

Coulomb’s Law There is an inverse square formula, called Coulomb’s law, for finding the force on one point charge due to another: K q 1 q 2 F= r 2 K = 9 109 N m 2 / C 2 This formula is just like Newton’s law of uniform gravitation with charges replacing masses and K replacing G. It states that the electric force on each of the point charges is directly proportional to each charge and inversely proportional to the square of the distance between them. The easiest way to use the formula to ignore signs when entering charges, since we already know that like charges repel and opposites attract. K is the constant of proportionality. Its units serve to reduce all units on the right to nothing but newtons. Forces are equal but opposite. + q 1 F Charges in Motion r F q 2 Coulomb's Law Detailed Example

Electric Force vs. Gravitational Force FE = K q 1 q 2 r 2 G m 1 m 2 FG = r 2 K = 9 109 N m 2 / C 2 G = 6. 67 10 -11 N m 2 / kg 2 Gravity is the dominant force when it comes to shaping galaxies and the like, but notice that K is about 20 orders of magnitude greater than G. Technically, they can’t be directly compared, since they have different units. The point is, though, that a whole lot of mass is required to produce a significant force, but a relatively small amount of charge can overcome this, explaining how the electric force on a balloon can easily match the balloon’s weight. When dealing with high-charge, low-mass objects, such as protons & electrons, the force of gravity is negligible.

Electric Force Example A proton and an electron are separated by 15 μm. They are released from rest. Our goal is to find the acceleration each undergoes at the instant of release. 1. Find the electric force on each particle. 1. 024 × 10 -18 N 2. Find the gravitational force on each particle. A proton’s mass is 1. 67 10 -27 kg, and an electron’s mass is 9. 11 10 -31 kg. 4. 51 × 10 -58 N 3. Find the net force on each and round appropriately. Note that the gravitational force is inconsequential here. 1. 024 × 10 -18 N 4. Find the acceleration on each particle. e-: 1. 124 × 1012 m/s 2, p+: 6. 13 × 108 m/s 2 5. Why couldn’t we use kinematics to find the time it would take the particles to collide? r changes, so F changes, so a changes. + 15 μm +

System of 3 Charges In a system of three point charges, each charge exerts a forces on the other two. So, here we’ve got a vector net force problem. Find the net force on charge B. Steps: 1. Find the distance in meters between A and B using the law of cosines. 0. 261947 m A +3 μC 2. Find angle B in the triangle using the law of sines. 36. 027932 º 3. Find FBA (the magnitude of the force on charge B due to charge A). 0. 786981 N 17 cm 4. Find FBC. 4. 591836 N 5. Break up the forces on B into components and find the net horiz. & vertical forces. 3. 78 N (right) , 1. 25 N (up) B 3. 98 N at 6. Determine Fnet on B. 18. 3 º N of E +2 μC 115º 14 cm C -5 μC

System of 4 Charges Here four fixed charges are arranged in a rectangle. Find Fnet on charge D. Solution: -16 µC A +25 µC C 767. 2 N at 59. 6 º N of W 4 cm B +9 µC Link 3 cm D -7 µC

Hanging Charge Problem Two objects of equal charge and mass are hung from the same point on a ceiling with equally long strings. They repel each other forming an angle between the strings. Find q as a function of m, L and . Solution: Draw a f. b. d. on one of the objects, break T into components, and write net vertical and horiz. equations: L L T FE q, m mg T sin( / 2) = FE , T cos( / 2) = mg. Dividing equations and using Coulomb’s law yields: mg tan( / 2) = FE = Kq 2 / r 2, where r = 2 L sin( / 2). Thus, 2 mg tan( / 2) sin 2( / 2) 4 L q= K

Point of Equilibrium Clearly, half way between two equal charges is a point of equilibrium, P, as shown on the left. (This means there is zero net force on any charge placed at P. ) At no other point in space, even points equidistant between the two charges, will equilibrium occur. Depicted on the right are two positive point charges, one with twice the charge of the other, separated by a distance d. In this case, P must be closer to q than 2 q since in order for their forces to be the same, we must be closer to the smaller charge. Since Coulomb’s formula is nonlinear, we can’t assume that P is twice as close to the smaller charge. We’ll call this distance x and calculate it in terms of d. Continued… x=? +q P +q +q P +2 q d

Point of Equilibrium Since P is the equilibrium point, no matter what charge is placed at P, there should be zero electric on it. Thus an arbitrary “test charge” q 0 (any size any sign) at P will feel a force due to q and an equal force due to 2 q. We compute each of these forces via Coulomb’s law: K q q 0 K (2 q) q 0 = 2 x (d - x)2 (cont. ) x +q +2 q d The K’s, q’s, and q 0’s cancel, the latter showing that the location of P is independent of the charge placed there. Cross multiplying we obtain: (d - x)2 = 2 x 2 d 2 - 2 x d + x 2 = 2 x 2 + 2 x d - d 2 = 0. P

Point of Equilibrium x (cont. ) From x 2 + 2 x d - d 2 = 0, the quadratic formula yields: x= -2 d (2 d )2 - 4 (1) (-d 2 ) = -d d 2 2 (1) P +q +2 q d = -2 d 8 d 2 2 Since x is a distance, we choose the positive root: x = d ( 2 - 1 ) 0. 41 d. Note that x < 0. 5 d, as predicted. Note that if the two charges had been the same, we would have d 2 - 2 x d + x 2 = x 2 d 2 - 2 x d = 0 d (d - 2 x ) = 0 x = d / 2, as started with (d - x)2 = x 2 predicted. This serves as a check on our reasoning.

Equilibrium with Several Charges Several equal point charges are to be arranged in a plane so that another point charge with non-negligible mass can be suspended above the plane. How might this be done? Answer: Arrange the charges in a circle, spaced evenly, and fix them in place. Place another charge of the same sign above the center of the circle. If placed at the right distance above the plane, the charge could hover. This arrangement works because of symmetry. The electric force vectors on the hovering charge are shown. Each vector is the same magnitude and they lie in a cone. Each vector has a vertical component and a component in the plane. The planar components cancel out, but the vertical components add to negate the weight vector. Continued…

Equilibrium with Several Charges (cont. ) Note that the charges in the plane are fixed. That is, they are attached somehow in the plane. They could, for example, be attached to an insulating ring, which is then set on a table. Regardless, how could the arrangement of charges in the plane be modified so as to maintain equilibrium of the hovering charge but allow it to hover at a different height? Answer: If the charges in the plane arranged in a circle with a large radius, the electric force vectors would be more horizontal, thereby working together less and canceling each other more. The hovering charge would lower. Since its weight doesn’t change, it must be closer to the plane in order to increase the forces to compensate for their partial cancellation. If the charges in the plane were arranged in a small circle, the vectors would be more vertical, thereby working together more and canceling each other less. The hovering charge would rise and the vectors would decrease in magnitude. To maximize the height of the hovering charge, all the charges in the plane should be brought to a single point. Continued…

Credits www. phys. ufl. edu/~phy 3054/elecstat/efield/twopoint/Welcome. html www. phys. ufl. edu/~phy 3054/elecstat/efield/polygon 4/Welcome. html www. eskimo. com/~billb/emotor/belt. html 207. 10. 97. 102/chemzone/lessons/03 bonding/mleebonding. htm chem. ch. huji. ac. il/~eugeniik/instruments/archaic/electroscopes. html www. physicsclassroom. com/mmedia/estatics/gep. html www. cutescience. com/files/collegephysics/movies/Ground. Positive. Rod. A. html
 Difference between charge and electric charge
Difference between charge and electric charge Difference between static and current electricity
Difference between static and current electricity Chapter 21 electric charge and electric field
Chapter 21 electric charge and electric field Chapter 21 electric charge and electric field
Chapter 21 electric charge and electric field Coloumb units
Coloumb units Dc o/d per item charge
Dc o/d per item charge Clasificacion de graff
Clasificacion de graff Gerald graff
Gerald graff Tanja gräff
Tanja gräff Clasificacion de graff
Clasificacion de graff Dr neill graff radford
Dr neill graff radford Kumulus ooforus
Kumulus ooforus Conservation of charge
Conservation of charge Continuity equation electromagnetism
Continuity equation electromagnetism Total charge formula
Total charge formula Electric field of a finite line charge
Electric field of a finite line charge Volume charge density symbol name
Volume charge density symbol name What is electric charge measured in
What is electric charge measured in Electric field around a positive charge
Electric field around a positive charge Section 1 electric charge crossword puzzle answers
Section 1 electric charge crossword puzzle answers Section 1 electric charge crossword puzzle answers
Section 1 electric charge crossword puzzle answers Section 1 electric charge
Section 1 electric charge Electric field of a finite line charge
Electric field of a finite line charge What is the potential at point a
What is the potential at point a Rubbing amber
Rubbing amber Charge on proton
Charge on proton Coulomb's equation
Coulomb's equation Sheet of charge electric field
Sheet of charge electric field Chapter 6 section 1 electric charge worksheet answers
Chapter 6 section 1 electric charge worksheet answers Electric field at a point formula
Electric field at a point formula Chapter 17 section 1 electric charge and force answer key
Chapter 17 section 1 electric charge and force answer key Electric field si units
Electric field si units Electric field lines about a point charge extend
Electric field lines about a point charge extend Section 1 electric charge
Section 1 electric charge Electric field of line charge
Electric field of line charge Electricity section 1 electric charge
Electricity section 1 electric charge Symbol of coulomb
Symbol of coulomb