Electric Forces and Fields AP Physics C Electrostatic

Electric Forces and Fields AP Physics C

Electrostatic Forces (F) (measured in Newtons) Given 2 charges of magnitude q 1 & q 2 separated by a distance d, the magnitude of the force that each of the charges exerts on the other is calculated by the relationship given by Coulomb’s Law. The direction of the force is determined by the fundamental law of charges (i. e. attraction or repulsion). The forces must be equal and opposite … Newton’s 3 rd Law! q 1 F F + F Coulomb’s Law: q 2 - d + + q 1 q 2 F k = 9 x 109 N*m 2/C 2 This is known as “Coulomb’s constant”

Electric Fields (E) measured in Newtons per Coulomb • Electric fields are the “energy field” that surrounds any charged particle” • Any other charge in this field will experience a force. • Electric fields are vectors (mag. & dir. ) • The direction of an Electric field is defined by the direction of the force on a “+” test charge placed in that field, thus Electric fields are always in a direction that is away from “+” and toward “-”. • Electric Field strength is measured in units of N/C (newtons per coulomb)

Force on a charge due to an Electric Field If a charge, q, is placed at point “x” in the field where the Electric Field strength is E, it will experience a force F. F E + q d Q +

Electric Potential Energy (Uelec) measured in Joules When two charges are placed near each other, they have the potential to start moving under the influence of the force between them. If they have the “potential” to have “kinetic energy” then according to the Law of Conservation of Energy, they must have Potential Energy when they are in that arrangement. To calculate the potential energy of this arrangement of charges… q 1 + d q 2 - Remember: energy of any kind is always a scalar quantity…magnitude only!

Charge Distributions Line charge density (or charge per unit of length) is represented by the greek letter lambda, λ, and calculated as , where Q is the total charge and L is the length, measured in C/m. ++++++++++++++++++ L Surface charge density (or charge per unit of area) is represented by the greek letter sigma, σ and calculated as and measured in C/m 2 ++++++++ +++++ Q is the total charge and A is the surface area of the charged object. You may need to know how to calculate the surface area of circle (disk), sphere, cube, or cylinder. Volume charge density, ρ is coming soon (Gauss’s Law…next)

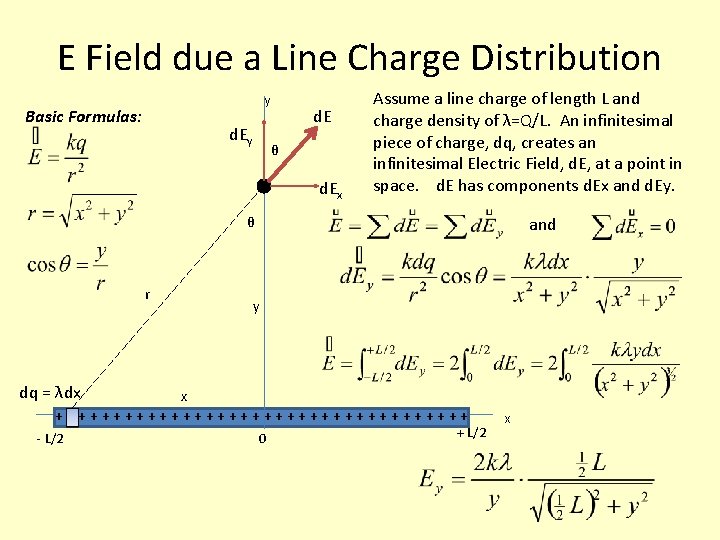
E Field due a Line Charge Distribution y Basic Formulas: d. Ey d. E θ d. Ex Assume a line charge of length L and charge density of λ=Q/L. An infinitesimal piece of charge, dq, creates an infinitesimal Electric Field, d. E, at a point in space. d. E has components d. Ex and d. Ey. and θ r dq = λdx y x ++++++++++++++++++ - L/2 0 + L/2 x

E Field on the Axis of a Ring of Charge Assume a ring of uniform charge distribution. Let dq be an infinitesimal piece of charge on the ring and d. E be the part of the total electric field at a point on the ring’s axis that is created by dq. Basic Formulas: dq + + + + a + + + + r x θ d. Ey and d. E

E field along the Axis of a Disk of Uniform Surface Charge Density da Assume a disk of total charge Q, radius R, and surface charge density σ=Q/A. Find the electric field at a point along the axis of the disk at a distance, x, away. a R Since we already know the equation for the field due to a ring of charge is: Then we substitute for dq: We will divide the disk into rings of radius a, infinitesimal width, da, and charge dq. Lets call the area of the disk A and the area of the ring d. A. If you imagine the ring straightened out into a rectangle you see that the area of the ring d. A = 2πa da. Since Q = σA, then dq = σda = 2πaσ da We can start with: We can now sum up (integrate) the rings from radius 0 to R…