Electric Potential Energy and Electric Potential In which

Electric Potential Energy and Electric Potential In which we recognize the benefit of conservative forces and energy conservation

Potential Energy Recall that potential energy (U) is the energy which is stored in a system. The potential energy of a system is the energy associated with the positions of the objects with respect to one another. Various types of potential energy can be defined, and each type corresponds to a particular conservative force. For example, Ug is associated with the gravitational force. Recall that a force is conservative when the work it does in moving an object is independent of the path between the object’s initial and final positions. Examples of conservative forces: gravity, spring force, electric force Potential energy is only one of a number of different varieties making up the total energy of a system. The total energy, E, of an isolated system is always conserved: E = 0 (isolated system) Moreover, when only conservative forces are present in an isolated system, the mechanical energy, Emech = K + U, is conserved. That is, there is no “loss” to thermal energy.

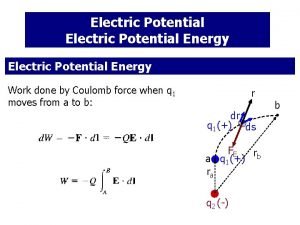
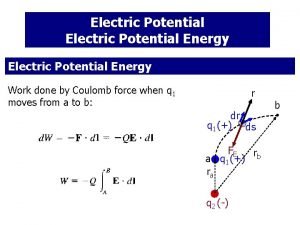
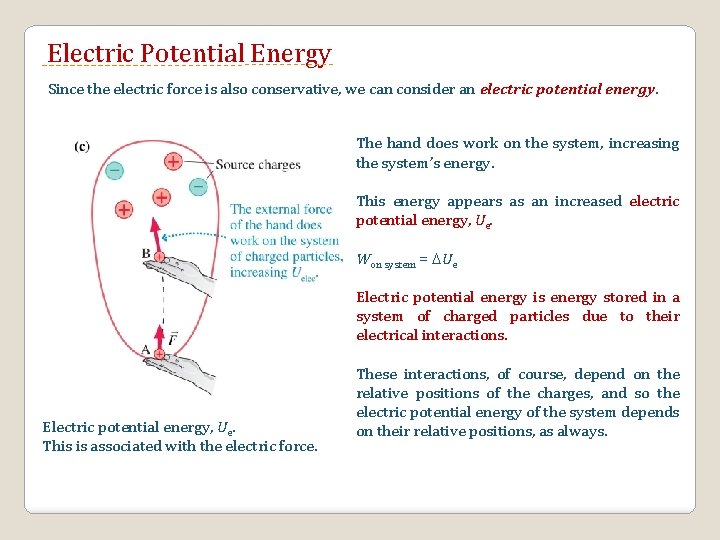
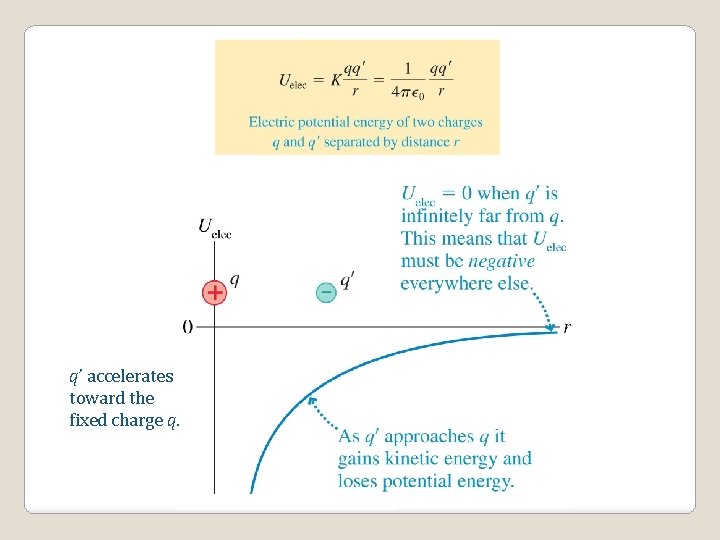
Electric Potential Energy Since the electric force is also conservative, we can consider an electric potential energy. The hand does work on the system, increasing the system’s energy. This energy appears as an increased electric potential energy, Ue. Won system = Ue Electric potential energy is energy stored in a system of charged particles due to their electrical interactions. Electric potential energy, Ue. This is associated with the electric force. These interactions, of course, depend on the relative positions of the charges, and so the electric potential energy of the system depends on their relative positions, as always.

Note: Strictly speaking, a particle by itself cannot have potential energy, since potential energy involves systems of particles. So when we say “the potential energy of the particle” we mean the particle and its system. Recall also that only changes in potential energy were meaningful. The actual value for the potential energy depends on the choice of a particular configuration of the system for which U = 0. Like all forms of potential energy, it is up to us to “set the zero” of the electric potential energy. That is, we must chose the point in space where we define Ue = 0.

We’ve seen that a charge creates an electric field in all the space surrounding it. This field exists whether or not a test charge is placed in the field. The electric field is what “communicates” the electric force: q 1 creates a field E, and q 2 interacts with this field, experiencing a force of magnitude Fon 2 = q 2 E. q 1 electric field every point in space has a vector E q 2 experiences F = q 2 E at a point Can we understand electric potential energy in a similar way? That is, does a single charge produce something in the space around it, such that if another charge is brought in, the system has an electric potential energy? Ue = q (? )

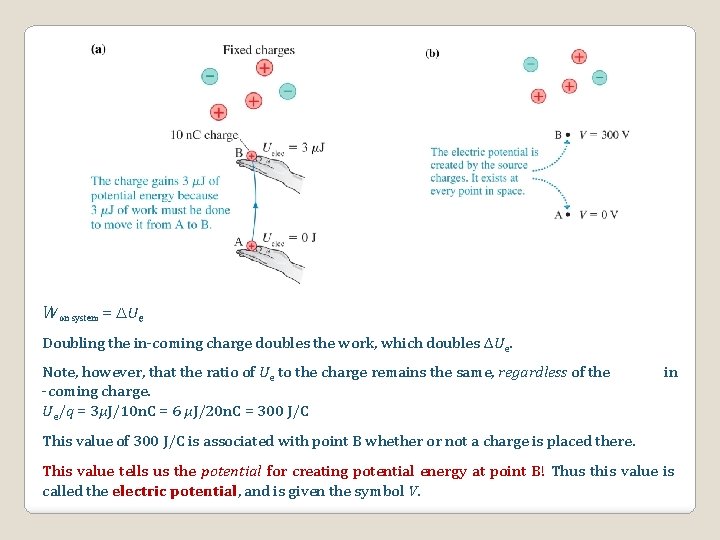
Won system = Ue Doubling the in-coming charge doubles the work, which doubles ΔUe. Note, however, that the ratio of Ue to the charge remains the same, regardless of the -coming charge. Ue/q = 3μJ/10 n. C = 6 μJ/20 n. C = 300 J/C in This value of 300 J/C is associated with point B whether or not a charge is placed there. This value tells us the potential for creating potential energy at point B! Thus this value is called the electric potential, and is given the symbol V.

The electric potential V at any point in space is the electric potential energy Ue per unit charge: V = Ue/q’ It’s important to understand that V is independent of the charge q’. We’ll soon see this. The unit of electric potential is the joule per coulomb, which is called the volt, V. 1 volt = 1 V = 1 J/C Unfortunately, we are stuck with some bad notation here: Electric potential is V, while its units are non-italicized V (volts) So we will have something like V = 200 V. Do not cancel the V’s! It may be easier to simply write “volts” rather than use V. V = 200 volts Electric potential is a scalar—it is just a number, with no direction. Electric potential can be positive, zero, or negative. The charges which produce the electric potential are referred to as the source charges.

What happens if we place another charge, a test charge q’, in the neighborhood of the source charges? If we place the test charge q’ at a point in space where the electric potential is V, the test charge will have an electric potential energy Ue = q’V. Notice that in this equation, q’ is the charge of the test particle. Also notice that there are no absolute value signs. Source charges create an electric potential in the space around them. At a point where the electric potential is V, the electric potential energy Ue of a particle with charge q’ is Ue = q’V Electric potential energy is measured in joules. It is a measure of the interaction energy of a charged particle q’ with the source charges producing V. Ue is proportional to the particles charge q’, and the potential V at which it is placed. Note that Ue can be positive, zero, or negative.

Since only changes in potential energy are significant, we often consider the equation Ue = q’ V (the change in Ue between two points) We call the quantity V = Vf - Vi the potential difference. The potential difference between two points in space is often called the voltage. potential difference = voltage = Vf - Vi We say that a particle moves “through” or “across” a potential difference. If a particle of charge q moves through a potential difference V, the change in its potential energy is Ue = q’ V. The electric force is conservative, so mechanical energy is conserved for a charged particle in an electric potential.

Example. The electric potentials at points A, B, and C are VA = 300 V, VB = 100 V, VC = -200 V. A 15 n. C charged particle moves from point A to point B to point C. By how much does the particle’s electric potential energy change between points A and C? Solution: Notice that we’re not told what is creating the electric potential. It exists independently of the 15 n. C charge. We can use Uelec = q. V to find the electric potential energy when charge q is placed at a point where the electric potential is V. We are interested in Uelec = (Uelec)C - (Uelec)A. Note that because the electric force is conservative, we don’t need to know the path; the information about B is not needed. (Uelec)C = q VC = ( 15 10 -9 C)(-200 V) = -3 J (Uelec)A = q VA = ( 15 10 -9 C)(300 V) = 4. 5 J Uelec = (Uelec)C - (Uelec)A = (-3 J) – (4. 5 J) = -7. 5 J A positive charged particle loses potential energy as it moves from a higher to a lower electric potential.

Energy conservation: Emech = 0 Emech = K + Ue = 0 K + q’ V = 0 This equation is important; it tells us how a particle’s speed changes when it moves through a potential difference V. Question: Is the same true for a negative charge? No! It’s just the opposite. To see why, keep in mind that Uelec = q V and not |q| V.

Example. A proton (q = 1. 6 10 -19 C, m = 9. 11 10 -27 kg) travelling with a speed of 2 105 m/s moves through a potential difference of +100 volts. What is the proton’s speed afterward? vf ? We’ll use conservation of energy: Now you calculate vf for an electron. A positive charge slows down when going to a higher potential (K U). A negative charge speeds up when going to a higher potential (U K).

A charge affects the space around it. We can look at this in two ways: It creates a vector field, which associates a vector E with each point in space. Or It creates a scalar field, which associates a scalar V with each point in space. + Suppose another charge is brought in Electric field picture: the electric field leads to an electric force Electric potential picture: the electric potential leads to an electric potential energy between the two

The electric potential produced by a single charge

The electric potential produced by a single charge

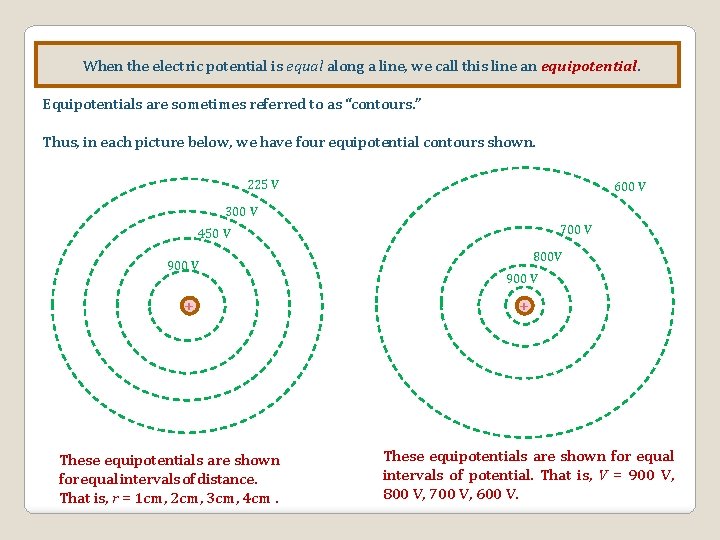
Let’s calculate a few values of the electric potential at different distances from a 1 n. C charge: V 1 cm = kq/d = (9 109 N m 2/C 2)(1 10 -9 C)/(. 01 m) = 900 V V 2 cm = kq/d = (9 109 N m 2/C 2)(1 10 -9 C)/(. 02 m) = 450 V V 3 cm = kq/d = (9 109 N m 2/C 2)(1 10 -9 C)/(. 03 m) = 300 V V 4 cm = kq/d = (9 109 N m 2/C 2)(1 10 -9 C)/(. 04 m) = 225 V Take a look at the first calculation. It says that at a distance of 1 cm from the charge, the electric potential is +900 V. But 1 cm away in which direction? In any direction! That is, there is a circle of radius 1 cm around the charge, and at every point on the circle the electric potential is + 900 V. The potential is equal along this circle. There is also a circle for each of the other potentials: 225 V 300 V 450 V 900 V +

When the electric potential is equal along a line, we call this line an equipotential. Equipotentials are sometimes referred to as “contours. ” Thus, in each picture below, we have four equipotential contours shown. 225 V 600 V 300 V 700 V 450 V 900 V + These equipotentials are shown for equal intervals of distance. That is, r = 1 cm, 2 cm, 3 cm, 4 cm. 800 V 900 V + These equipotentials are shown for equal intervals of potential. That is, V = 900 V, 800 V, 700 V, 600 V.

600 V 700 V 800 V 900 V + This way is perhaps preferable. Notice that the more closely spaced equipotential lines indicate a “steepness” in the potential. This will be important when we connect the electric potential with the electric field. These equipotentials are shown for equal intervals of potential.

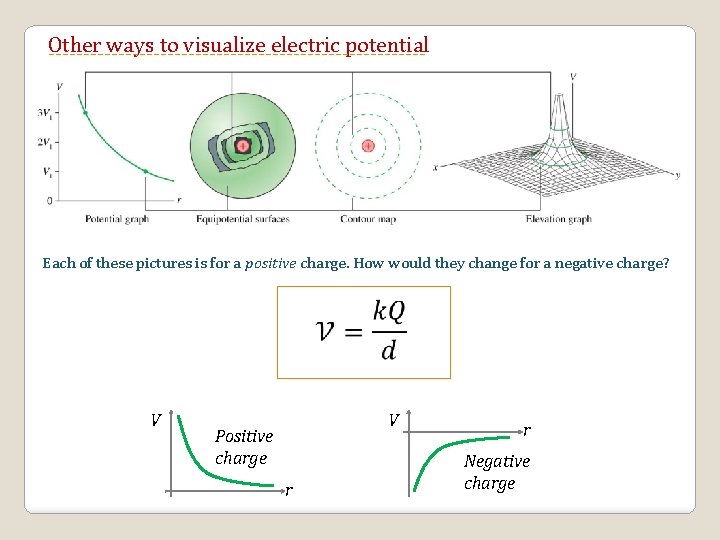
Other ways to visualize electric potential Each of these pictures is for a positive charge. How would they change for a negative charge? V V Positive charge r r Negative charge

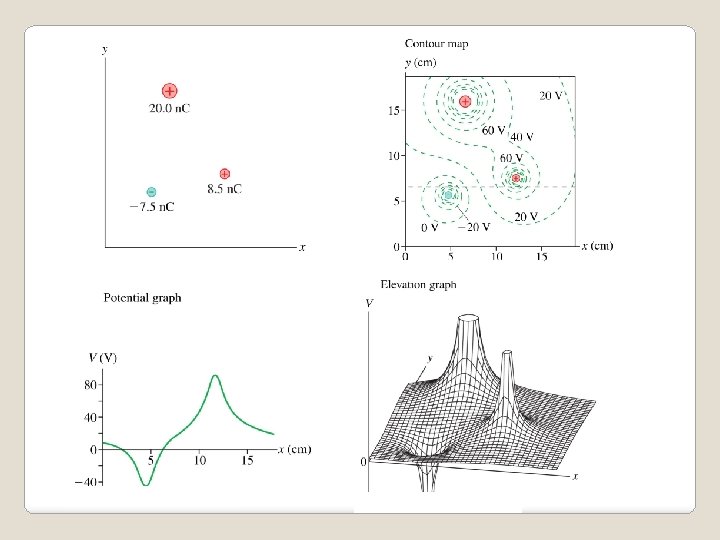
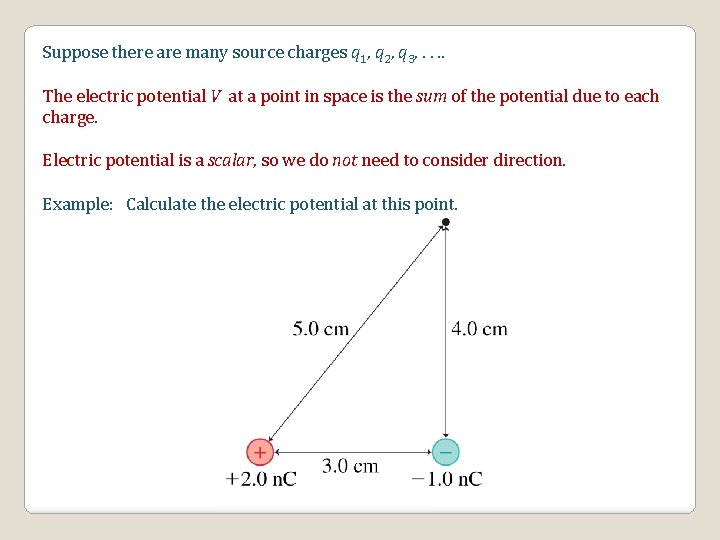
Suppose there are many source charges q 1, q 2, q 3, . . The electric potential V at a point in space is the sum of the potential due to each charge. Electric potential is a scalar, so we do not need to consider direction. Example: Calculate the electric potential at this point.

We have already seen that if there is an electric potential V at a point in space, and we put a charge q’ at that location, the electric potential energy will be given by Uelec = q’ V. Since V = Kq/r, we have for the electric potential energy the following equation:

q’ accelerates toward the fixed charge q.

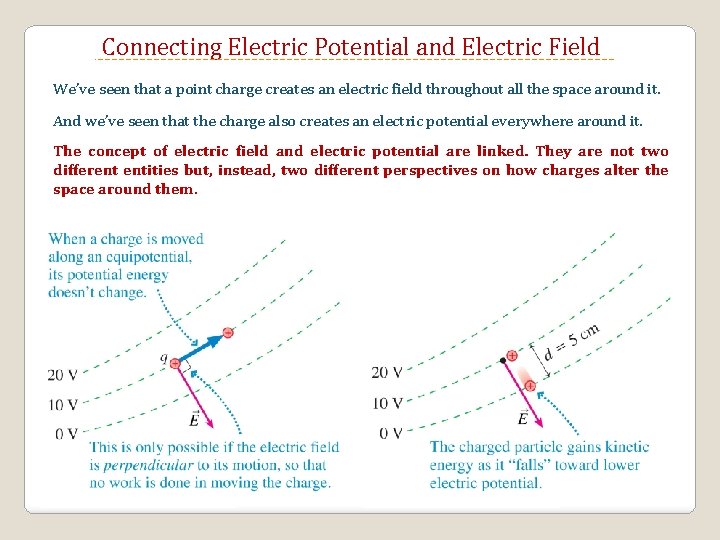
Connecting Electric Potential and Electric Field We’ve seen that a point charge creates an electric field throughout all the space around it. And we’ve seen that the charge also creates an electric potential everywhere around it. The concept of electric field and electric potential are linked. They are not two different entities but, instead, two different perspectives on how charges alter the space around them.

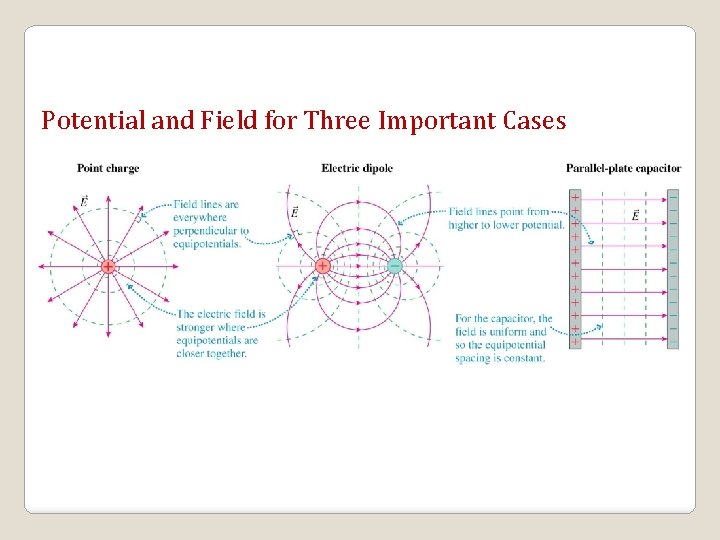
Potential and Field for Three Important Cases

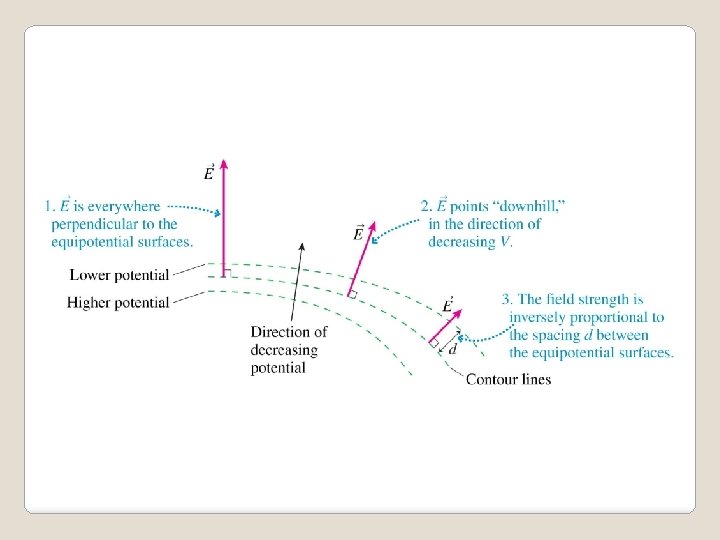
c There is an electric field in the x direction only if the potential changes as you move in the x direction. This goes for any direction—x, y, or z. The electric field is the negative of the slope of the electric potential. What is the electric field strength between the two equipotentials?

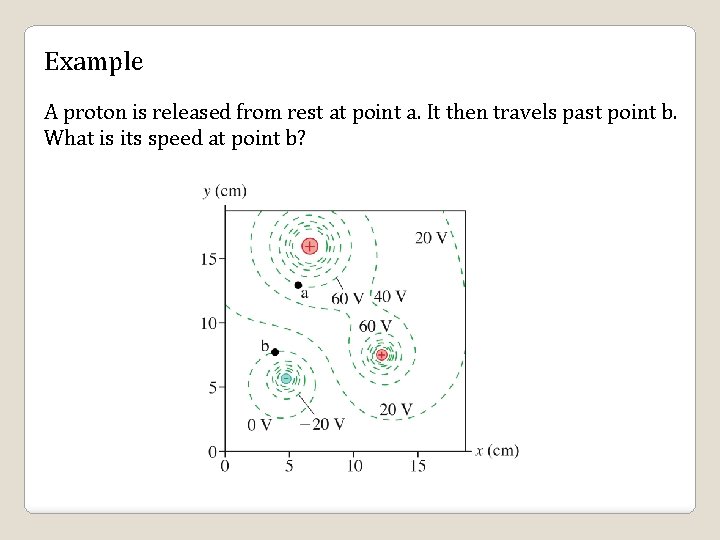
Example A proton is released from rest at point a. It then travels past point b. What is its speed at point b?

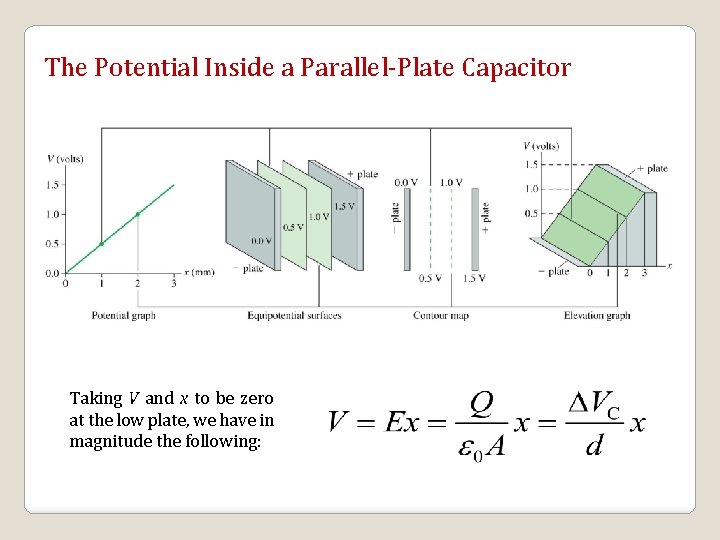
The Potential Inside a Parallel-Plate Capacitor Taking V and x to be zero at the low plate, we have in magnitude the following:

Example 1 James recharges his dead 12 V battery by sending 28, 000 C of charge through the terminals. How much work was required to charge the battery? How much electric potential energy is stored in the battery when it is charged?

Example 2 If an electron gains 1. 4 × 10 -15 J of energy when it is accelerated through a TV tube, what voltage was applied across the tube?

Example 3 The two plates of a “bug zapper” are 5 cm apart. The electric field between the plates is 2. 8 × 106 V/m. What is the voltage (the potential difference) across the plates?

Example 4 While getting out of his car, Victor builds up a charge on his body. When he gets out and shuts the door, his hand discharges 12, 000 V through an electric field of 3× 106 V/m. How far was his hand from the door at the time he got shocked?

Example 5 A lightning bolt travels 200 m through an electric field of 2 × 106 V/m and strikes a tree. What is the potential difference between the cloud and tree?