Chapter 17 Electric Potential Electric Energy and Capacitance

Chapter 17 Electric Potential, Electric Energy and Capacitance © 2006 Giancoli, PHYSICS, 6/E © 2005. Electronically reproduced by permission of Pearson Education, Inc. , Upper Saddle River, New Jersey Ch 17 1

Review of Work and Energy Electric potential is based on the concept of work and energy. • Work = (force) (distance) (cos ) • Units are J (joules) 1 J = N m • Potential Energy is energy of position such as the energy stored in a stretched spring or a roller coaster at the top of the first hill. • You have to do work to move a positive charge in an electric field to point a, so that charge has electrical potential energy (PEa). • If you release the charge it will “fall” away from the other charge thus gaining kinetic energy KE = ½ m v 2 Ch 17 2

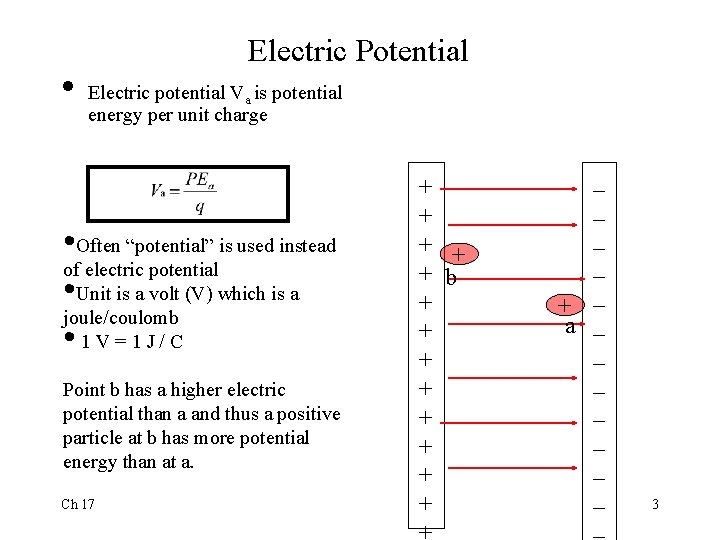
• Electric Potential Electric potential Va is potential energy per unit charge • Often “potential” is used instead of electric potential • Unit is a volt (V) which is a joule/coulomb • 1 V=1 J/C Point b has a higher electric potential than a and thus a positive particle at b has more potential energy than at a. Ch 17 + + + b + + + + _ _ + _ a _ _ _ _ 3

Potential Difference • The difference in potential energy between two points a and b is the work done in moving a charge from one point to the other Wba ( assuming the charge is moved slowly so there in no change in kinetic energy. ) It is similar with electric potential. • Ch 17 4

• Potential Energy Difference Since electric potential is potential energy per unit charge, we can find the change in potential energy Example 17 -1: The two parallel plates shown are connected to a 9 V battery. If a charge of +4 C is located at point b then the potential energy difference between b and a is PE = (9 V) (4 C)= 36 J • If the charge were released at point b it would accelerate towards a and gain 36 J of kinetic energy if there was no friction. Ch 17 + + + b + + + + _ _ a _ _ _ _ 5

The Electron Volt • Many devices accelerate electrons and protons through a given potential difference • Because all charges are e or multiples of e, a special unit of energy has been created called the electron volt • Definition: An electron volt (e. V) is the energy gained or lost when a particle of charge e moves through a potential difference of 1 V. • 1 e. V = q V = (1. 60 x 10 C)( 1. 0 V) = 1. 60 x 10 -19 J Ch 17 -19 6

Example 17 -2: An electron in a TV tube is accelerated through a potential difference of 25, 000 V. What is the kinetic energy of the electron in electron volts? Answer: KE = 25, 000 e. V What is the kinetic energy in J? We use the conversion factor KE = 25, 000 e. V (1. 6 x 10 -19 J/e. V) = 4. 0 x 10 -15 J Ch 17 7

The Electron Volt Example 17 -3: A 42 He nucleus is accelerated from rest through a potential difference of 750, 000 V. What is the kinetic energy of the nucleus? The standard notation is AZX. where A is the number of nucleons (protons and neutrons) and Z is the number of protons. Thus this nucleus has a charge = +2 e. We could also refer to this as a He 2+ ion. Answer: In this case the charge is 2 e and thus the kinetic energy is twice as great as when a singe proton is accelerated. KE = 2 (750, 000 e. V) = 1. 5 x 106 e. V = 1. 5 Me. V Ch 17 8

Electric Field of Parallel Plates • • • Consider the uniform electric field between parallel plates Ignoring signs the work done by the field to move the charge from b to a is W= q Vba Since the E field is uniform, we can also calculate W from W=Fd=q. Ed We can combine these two equations to give Vba = E d The electric field between parallel conducting plates is thus + + b + + + + _ _ _ + _ a _ _ _ _ This equation can be used anywhere the electric field is uniform. Ch 17 9

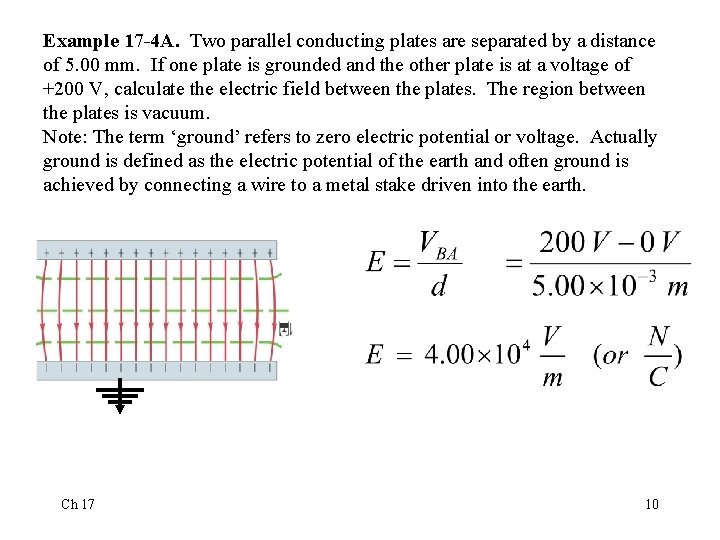
Example 17 -4 A. Two parallel conducting plates are separated by a distance of 5. 00 mm. If one plate is grounded and the other plate is at a voltage of +200 V, calculate the electric field between the plates. The region between the plates is vacuum. Note: The term ‘ground’ refers to zero electric potential or voltage. Actually ground is defined as the electric potential of the earth and often ground is achieved by connecting a wire to a metal stake driven into the earth. Ch 17 10

Example 17 -4 B. If an electron is released near the grounded plate in Ex. 17 -4 A, what is its kinetic energy in e. V and J when it reaches the + 200 V plate. . Also calculate the velocity of the electron at that time. Ch 17 11

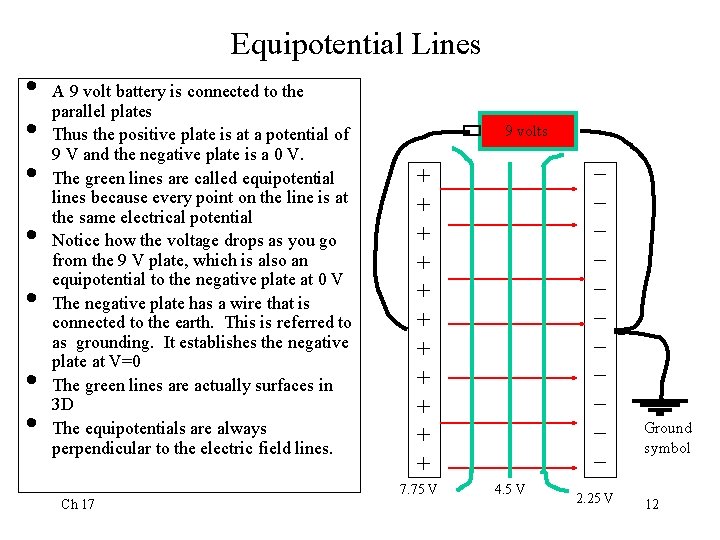
Equipotential Lines • • A 9 volt battery is connected to the parallel plates Thus the positive plate is at a potential of 9 V and the negative plate is a 0 V. The green lines are called equipotential lines because every point on the line is at the same electrical potential Notice how the voltage drops as you go from the 9 V plate, which is also an equipotential to the negative plate at 0 V The negative plate has a wire that is connected to the earth. This is referred to as grounding. It establishes the negative plate at V=0 The green lines are actually surfaces in 3 D The equipotentials are always perpendicular to the electric field lines. Ch 17 9 volts _ _ _ + + + 7. 75 V 4. 5 V 2. 25 V Ground symbol 12

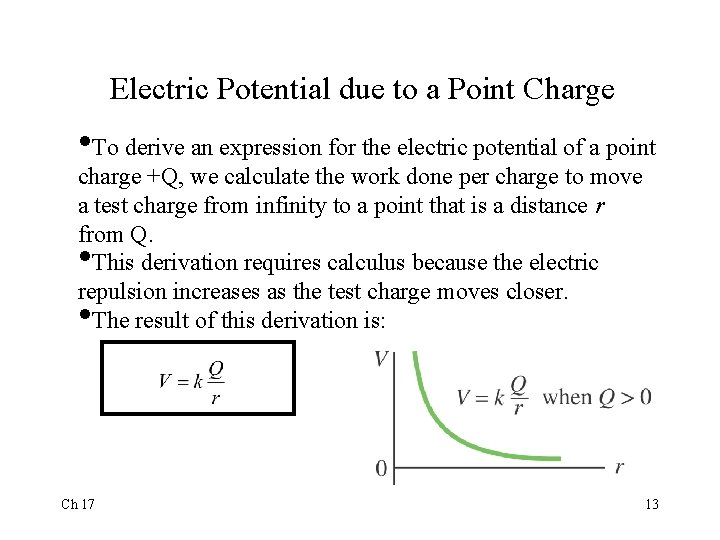
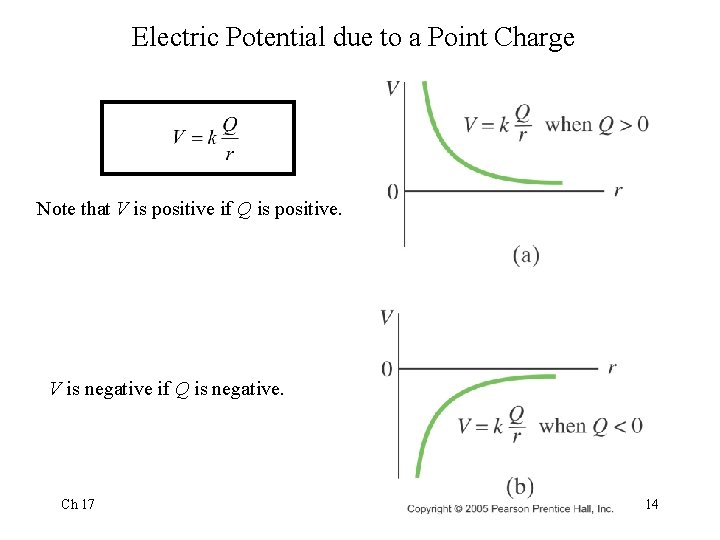
Electric Potential due to a Point Charge • To derive an expression for the electric potential of a point charge +Q, we calculate the work done per charge to move a test charge from infinity to a point that is a distance r from Q. This derivation requires calculus because the electric repulsion increases as the test charge moves closer. The result of this derivation is: • • Ch 17 13

Electric Potential due to a Point Charge Note that V is positive if Q is positive. V is negative if Q is negative. Ch 17 14

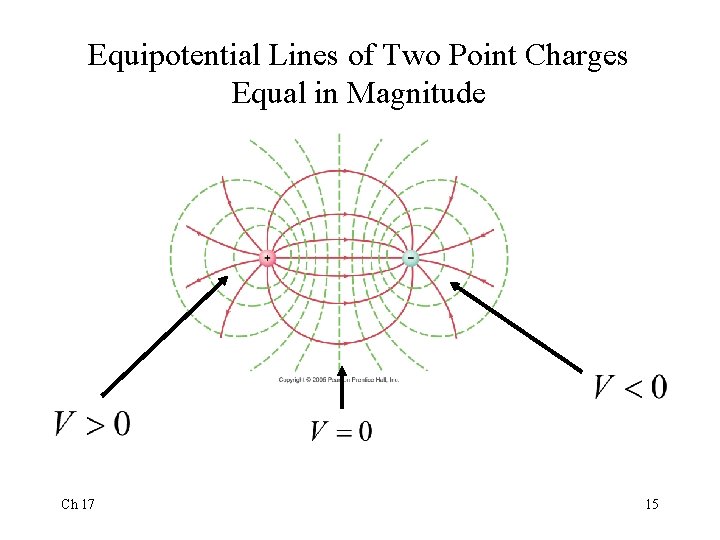
Equipotential Lines of Two Point Charges Equal in Magnitude Ch 17 15

Example 17 -5 A. Calculate the electric potential of the upper right corner of a rectangle that is 3. 0 cm high and 6. 0 cm long if there are charges of +8. 0 C in the upper left corner, +2. 0 C in the lower left corner and +4. 0 C in the lower right corner. Assume V = 0 at infinity. Ch 17 16

Example 17 -5 B. For the problem above, how much work would be done in bringing a proton from infinity to the upper right corner? Ch 17 17

The Capacitor • • What would happen to the charged parallel plates if the battery were disconnected? Answer: Nothing: the + and – charges are attracted to each other, so they would remain. Notice that this is a charge-storage device. It also stores energy. The potential difference or voltage V will remain constant This device is called a capacitor and it is often used in electrical circuits. Often the plates are made of a thin foil with a thin insulator between the plates. This can then be rolled up to form a very compact device Ch 17 9 volts + + + _ _ _ 18

Capacitor Equations There are several equations that describe the capacitor which we will not derive. • The charge on the plate is proportional to the voltage: • Q is the charge on one plate (and there is an equal but opposite charge on the other plate) and V is the voltage difference. • We refer to C as the capacitance. • The unit of capacitance is the farad ( F ). • 1 F=1 C/V • Most capacitors are F or smaller Ch 17 + + + _ _ _ 19

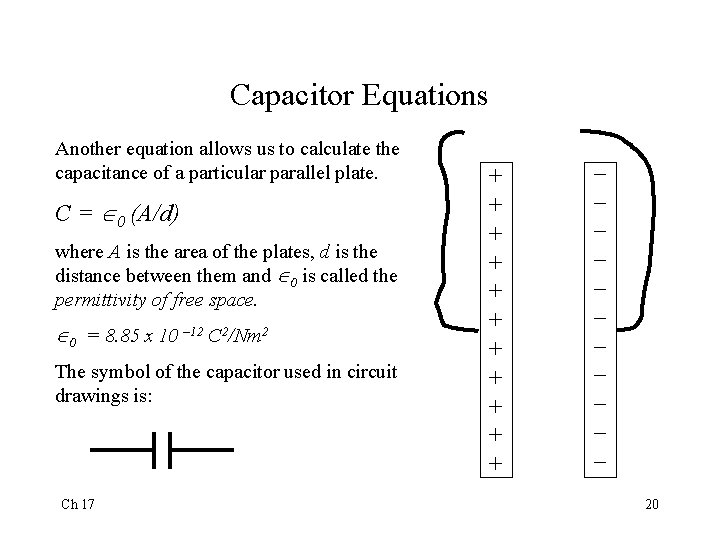
Capacitor Equations Another equation allows us to calculate the capacitance of a particular parallel plate. C = 0 (A/d) where A is the area of the plates, d is the distance between them and 0 is called the permittivity of free space. 0 = 8. 85 x 10 – 12 C 2/Nm 2 The symbol of the capacitor used in circuit drawings is: Ch 17 + + + _ _ _ 20

Dielectrics Most capacitors have a dielectric material between the plates that • Increases capacitance • Allows higher voltages • Maintains distance d • The formula for a capacitor with a dielectric is (this is the formula to remember). C = K 0 ( A / d ) where K is the dielectric constant. Ch 17 21

Dielectrics Dielectric Constants of some materials at 20 o. C. The dielectric constant is unitless Ch 17 Vacuum 1. 0000 Air 1. 0006 Vinyl (plastic) 2. 8 4. 5 Mica 7 Water 80 22

How Dielectrics Work • The molecules in dielectrics become polar which means that the electrons tend to be located closer to the positive plate as shown below. • A test charge inside the dielectric feels a E field reduced by 1 / K and thus a smaller V. Ch 17 + + + + -+ -+ -+ -+ -+ -+ _ _ _ _ 23

Energy Storage in a Capacitor A battery must do work to move electrons from one plate to the other. The work done to move a small charge q across a voltage V is W = V q. As the charge increases, V increases so the work to bring q increases. Using calculus we find that the energy ( U ) stored on a capacitor is given by: Ch 17 24

Example 17 -6 A. A parallel-plate capacitor has an area of 5. 00 cm 2, and the plates are separated by 1. 00 mm with air (K = 1. 0006) between them. Calculate the capacitance. 17 -6 B. If the above capacitor is storing a charge of 400 p. C, what is the voltage across the plates? Ch 17 25

17 -6 C What is the energy stored by the capacitor? 17 -6 D If mica (K = 7. 0) is placed between the plates of the above capacitor, calculate its capacitance. Ch 17 26

Cathode Ray Tube (CRT) • Electrons are ejected from heated metal called cathode • Then accelerated through potential difference of as much as 25, 000 V • Electron beam is then bent by horizontal and vertical electric fields created by the horizontal and vertical deflection plates. • Electron beam then strikes fluorescent screen • Points on screen fluoresce in different colors • Electronics attached to deflection plates cause beam to paint a picture on screen • Picture made with 525 horizontal lines • Picture redrawn at 30 Hz Ch 17 27