Electric Potential Chapter 25 Electric Potential Energy Electric

Electric Potential Chapter 25 Electric Potential Energy Electric Potential Equipotential Surfaces

Electric Potential: the Bottom Line The electric potential V(r) is an easy way to calculate the electric field – easier than directly using Coulomb’s law. For a point charge at the origin: For a collection of charges qi at positions ri the electric potential at r is the scalar sum: Calculate V and then find the electric field by taking the gradient:

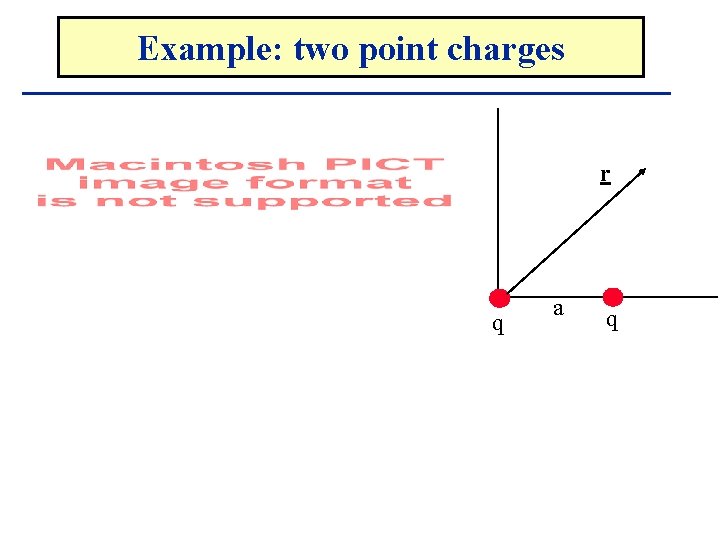
Example: two point charges r q a q

CONSERVATIVE FORCES A conservative force “gives back” work that has been done against it When the total work done by a force on an object moving around a closed loop is zero, then the force is conservative ° F·dr = 0 F is conservative The circle on the integral sign indicates that the integral is taken over a closed path The work done by a conservative force, in moving and object between two points A and B, is independent of the path taken W= AB F·dr is a function of A and B only – it is NOT a function of the path selected. We can define a potential energy difference as UAB=-W.

POTENTIAL ENERGY The change UAB in potential energy due to the electric force is thus UAB = -q AB E·dr UAB = UB – UA = potential energy difference between A and B Potential energy is defined at each point in space, but it is only the difference in potential energy that matters. Potential energy is measured with respect to a reference point (usually infinity). So we let A be the reference point (i. e, define UA to be zero), and use the above integral as the definition of U at point B.

POTENTIAL ENERGY IN A CONSTANT FIELD E E L A • dl • B The potential energy difference between A and B equals the work necessary to move a charge +q from A to B UAB = UB – UA = - q E·dl But E = constant, and E. dl = -E dl, so: UAB = - q E · dl = q E dl = q E L UAB = q E L

ELECTRIC POTENTIAL DIFFERENCE The potential energy U depends on the charge being moved. To remove this dependence, we introduce the concept of the electric potential V. This is defined in terms of the difference V: VAB = UAB / q = - AB E · dl Electrical Potential = Potential Energy per Unit Charge = line integral of -E·dl VAB = Electric potential difference between the points A and B. Units are Volts (1 V = 1 J/C), and so the electric potential is often called the voltage. A positive charge is pushed from regions of high potential to regions of low potential.

ELECTRIC POTENTIAL IN A CONSTANT FIELD E E L A • d. L • B VAB = UAB / q The electrical potential difference between A and B equals the work per unit charge necessary to move a charge +q from A to B VAB = VB – VA = - E·dl But E = constant, and E. dl = -1 E dl, so: VAB = - E·dl = E dl = E L VAB = E L UAB = q E L

Cases in which the electric field E is not aligned with dl E A VAB = - AB E · dl • • B The electric potential difference does not depend on the integration path. So pick a simple path. One possibility is to integrate along the straight line AB. This is convenient in this case because the field E is constant, and the angle between E and dl is constant. B E. dl = E dl cos VAB = - E cos dl = - E L cos A

Cases in which the electric field E is not aligned with dl E A • L d • • C VAB = - AB E · dl B Another possibility is to choose a path that goes from A to C, and then from C to B VAB = VAC + VCB Thus, VAB = E d VAC = E d VCB = 0 (E d. L) but d = L cos = - L cos VAB = - E L cos

Equipotential Surfaces (lines) A E B For a constant field E VAB = E L x L E Similarly, at a distance x from plate A VAx = E x All the points along the dashed line at x, are at the same potential. The dashed line is an equipotential line L

Equipotential Surfaces (lines) x E It takes no work to move a charge at right angles to an electric field E dl E • dl = 0 V = 0 L If a surface(line) is perpendicular to the electric field, all the points in the surface (line) are at the same potential. Such surface (line) is called EQUIPOTENTIAL ELECTRIC FIELD

Equipotential Surfaces We can make graphical representations of the electric potential in the same way as we have created for the electric field: Lines of constant E

Equipotential Surfaces We can make graphical representations of the electric potential in the same way as we have created for the electric field: Lines of constant V (perpendicular to E) Lines of constant E

Equipotential Surfaces We can make graphical representations of the electric potential in the same way as we have created for the electric field: Lines of constant V (perpendicular to E) Lines of constant E Equipotential plots are like contour maps of hills and valleys. A positive charge would be pushed from hills to valleys.

Equipotential Surfaces How do the equipotential surfaces look for: (a) A point charge? E + (b) An electric dipole? + - Equipotential plots are like contour maps of hills and valleys. Equipotential plots are like contourfrom mapshills of hills and valleys. A positive charge would be pushed to valleys.

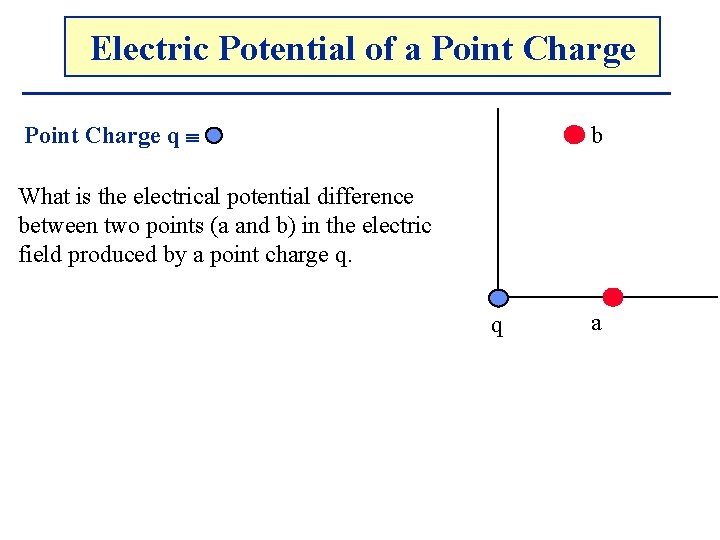
Electric. The Potential Electricof. Potential a Point Charge q b What is the electrical potential difference between two points (a and b) in the electric field produced by a point charge q. q a

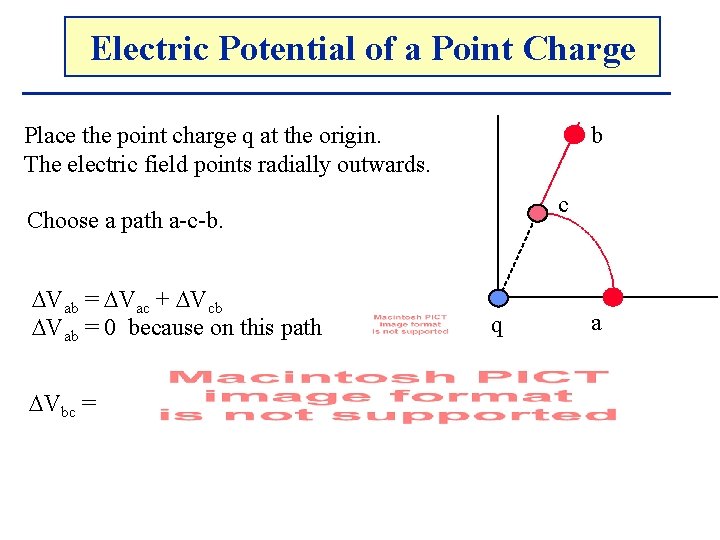
Electric. The Potential Electricof. Potential a Point Charge b Place the point charge q at the origin. The electric field points radially outwards. c Choose a path a-c-b. Vab = Vac + Vcb Vab = 0 because on this path Vbc = q a

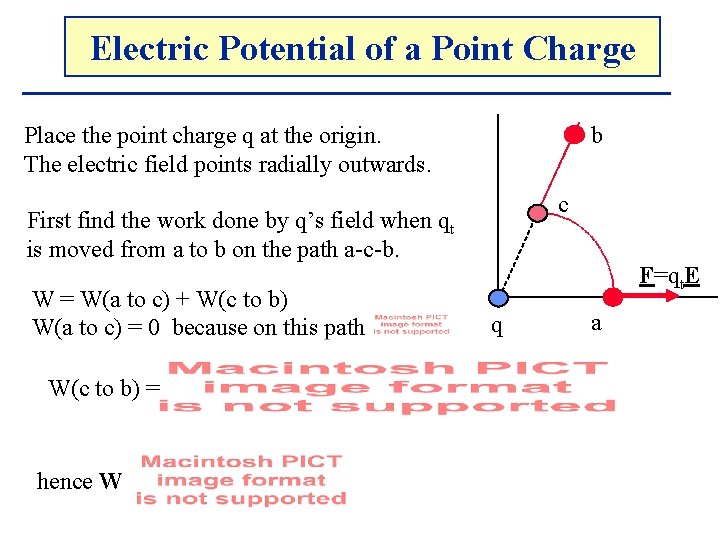
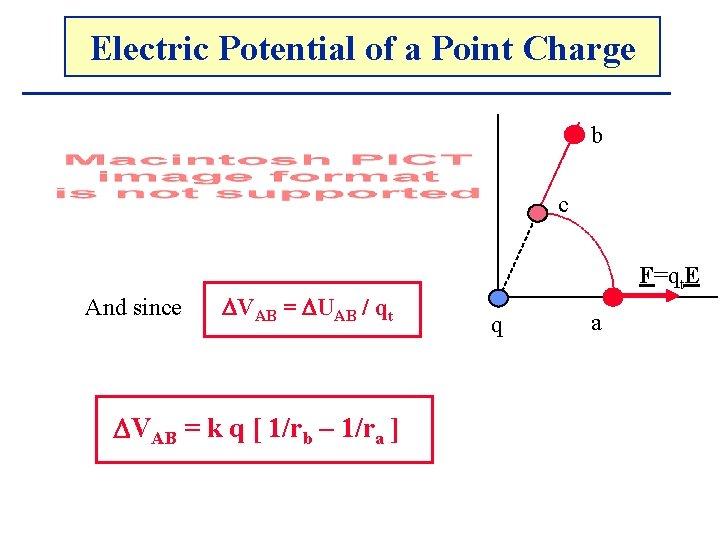
Electric. The Potential Electricof. Potential a Point Charge b Place the point charge q at the origin. The electric field points radially outwards. c First find the work done by q’s field when qt is moved from a to b on the path a-c-b. W = W(a to c) + W(c to b) W(a to c) = 0 because on this path W(c to b) = hence W F=qt. E q a

Electric. The Potential Electricof. Potential a Point Charge b c And since VAB = UAB / qt VAB = k q [ 1/rb – 1/ra ] F=qt. E q a

Electric. The Potential Electricof. Potential a Point Charge b VAB = k q [ 1/rb – 1/ra ] c From this it’s natural to choose the zero of electric potential to be when ra Letting a be the point at infinity, and dropping the subscript b, we get the electric potential: V=kq/r F=qt. E q When the source charge is q, and the electric potential is evaluated at the point r. Remember: this is the electric potential with respect to infinity a

Potential Due to a Group of Charges • For isolated point charges just add the potentials created by each charge (superposition) • For a continuous distribution of charge …

Potential Produced by a Continuous Distribution of Charge In the case of a continuous distribution of charge we first divide the distribution up into small pieces, and then we sum the contribution, to the electric potential, from each piece: dqi

Potential Produced by a Continuous Distribution of Charge In the case of a continuous distribution of charge we first divide the distribution up into small pieces, and then we sum the contribution, to the electric potential, from each piece: In the limit of very small pieces, the sum is an integral A r d. V = k dq / r A dq Remember: VA = d. VA = k dq / r vol k=1/(4 0)

Example: a disk of charge Suppose the disk has radius R and a charge per unit area s. Find the potential at a point P up the z axis (centered on the disk). Divide the object into small elements of charge and find the potential d. V at P due to each bit. For a disk, a bit (differential of area) is a small ring of width dw and radius w. P dq = s 2 wdw z r dw w R