Electric Potential and Electric Potential Energy Learning Objectives

Electric Potential and Electric Potential Energy

Learning Objectives • To introduce the concept of electric potential energy • To define the electric potential • To find and use the electric potential of point charges, charged spheres, and parallel-plate capacitors • To understand charge and energy storage in a capacitor

Remember Work? • In high school we learned that Work = force x displacement* • Work is a scalar, unlike force and displacement, which are vectors. • If the force and the displacement are in the same direction, the work is positive; if they are in opposite directions, the work is negative. • The electric field generates a force that does work. *oversimplified, but it will do for now

Question about Work Which of the following is true for the proton as it travels from point A to point B? Blue arrow shows force on proton due to E field. A. Work done on the charge is positive. B. Work done on the charge is negative. C. No work is done on the charge

Another Question about Work Which of the following is true for the electron as it travels from point B to point A this time? Blue arrow shows force on electron due to E field. A. Work done on the charge is positive. B. Work done on the charge is negative. C. No work is done on the charge.

More about work • When a conservative force does work, this work is defined as the change in potential energy of an object. • Conservative forces include electric force, magnetic force, gravity, the spring force and the Tea Party. All other forces we deal with in this class are nonconservative.

The change in potential energy ΔPE = - Wconservative As the weight goes up, its potential energy increases, so ΔPE is positive. The gravitational force is doing negative work, since it’s direction (down) is opposite to that of the displacement(up) Knight uses ΔU for the change in potential energy: (ΔU = - Wconservative )

The change in potential energy ΔPE = - Wconservative As the weight goes down, its potential energy decreases so ΔPE is negative. The gravitational force is doing positive work, since it’s direction (down) is same as that of the displacement (down).

Question about ΔEPE Which of the following is true for the electron as it travels from point B to point A? Blue arrow shows force on electron due to E field. A. ΔEPE is positive. B. ΔEPE is negative. C. EPE does not change.

Conservation of Energy W nonconservative = ΔKE + ΔPE Non-conservative forces that do work include pushes and pulls, friction, tension and the ACLU. If no conservative forces do work on a system: W nonconservative = ΔKE If no nonconservative forces do work: ΔKE + ΔPE = 0

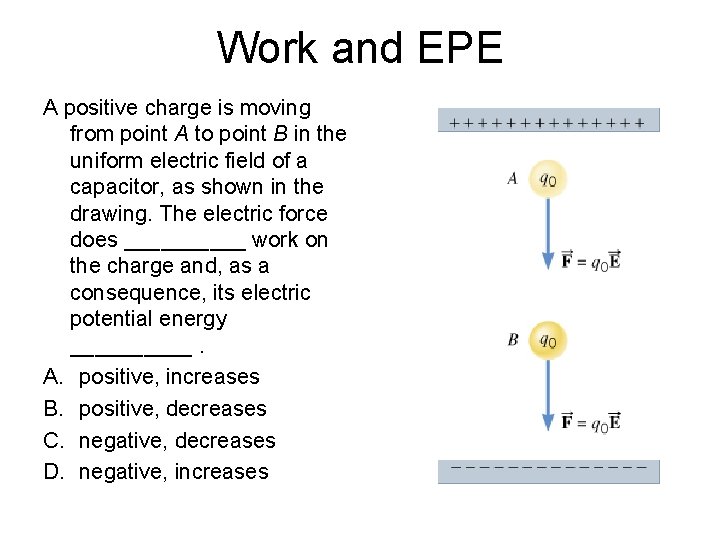
Work and EPE A positive charge is moving from point A to point B in the uniform electric field of a capacitor, as shown in the drawing. The electric force does _____ work on the charge and, as a consequence, its electric potential energy _____. A. positive, increases B. positive, decreases C. negative, decreases D. negative, increases

EPE and KE - 1 A small, positively-charged particle is shot toward a larger fixed charge, also positive. There are no nonconservative forces once the particle is released What does the particle do? A. B. C. D. speed up and gain EPE slow down and gain EPE speed up and lose EPE slow down and lose EPE fixed

EPE and KE- 2 A small, positively-charged particle is shot toward a larger fixed charge, this time negative. What does the particle do? A. B. C. D. speed up and gain EPE slow down and gain EPE speed up and lose EPE slow down and lose EPE

The Electric Potential Model • The source charges have altered the space around them to create an electric field (E). • Any point in the E field has an electric potential (V) associated with it. • A test charge q (blue) at that point has an EPE. • V = EPE/q

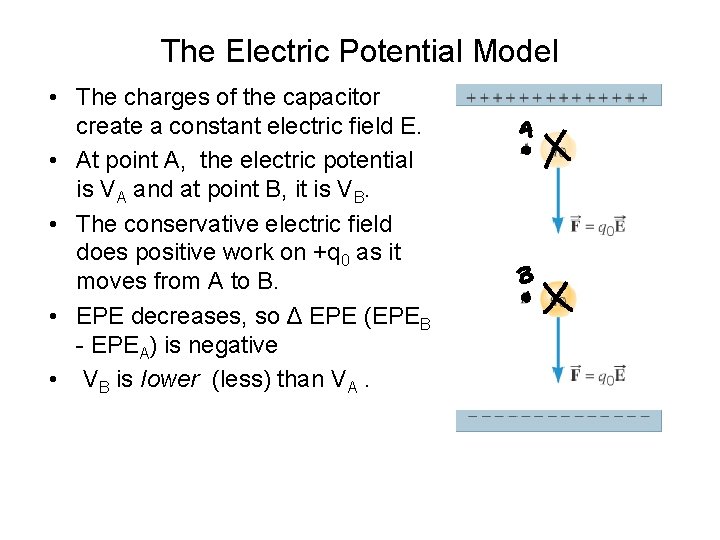
The Electric Potential Model • The charges of the capacitor create a constant electric field E. • At point A, the electric potential is VA and at point B, it is VB. • The conservative electric field does positive work on +q 0 as it moves from A to B. • EPE decreases, so Δ EPE (EPEB - EPEA) is negative • VB is Iower (less) than VA.

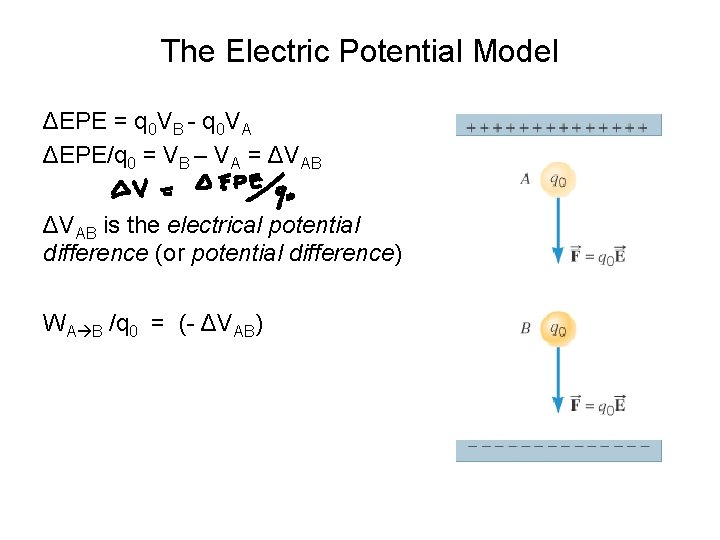
The Electric Potential Model ΔEPE = q 0 VB - q 0 VA ΔEPE/q 0 = VB – VA = ΔVAB is the electrical potential difference (or potential difference) WA B /q 0 = (- ΔVAB)

19. 2 The Electric Potential Difference DEFINITION OF ELECTRIC POTENTIAL DIFFERENCE The electric potential difference between 2 points is the change in electric potential energy experienced by a test charge as it moved between the 2 points, divided by the charge itself. The change in electric potential energy is the negative of the work done by the electric field when the charge moves between the 2 points SI Unit of Electric Potential Difference: joule/coulomb = volt (V)

19. 2 The Electric Potential Difference DEFINITION OF ELECTRIC POTENTIAL The electric potential at a point is the electric potential energy of a small test charge divided by the charge itself: SI Unit of Electric Potential: joule/coulomb = volt (V) Recall that any value for a potential energy is based on an arbitrary zero. The same is true for the electric potential. Only the differences ΔEPE and ΔV can be measured absolutely in terms of the work done between 2 points.

Potential and Potential Energy As the +1 n. C charge moves toward the source charges, it gains 1 μJ of potential energy. The change in potential is: A. 1 KV B. 1 μV C. 1 m. V D. 1 n. V

Sources of Electric Potential Difference A potential difference is created by separating positive charge from negative charge.

Measuring Electric Potential Difference • The voltmeter measures the potential difference (ΔV) between 2 points. • Since it is the difference that is important, not the actual value, the black lead is 0 volts and the value read by the voltmeter is equal to (ΔV).

Work and potential difference In each of the cases below, the same +q 0 moves from points A to B. In which case is the most work done by the electric field? A. Case 1 C. Case 3 B. Case 2 D. All equal work

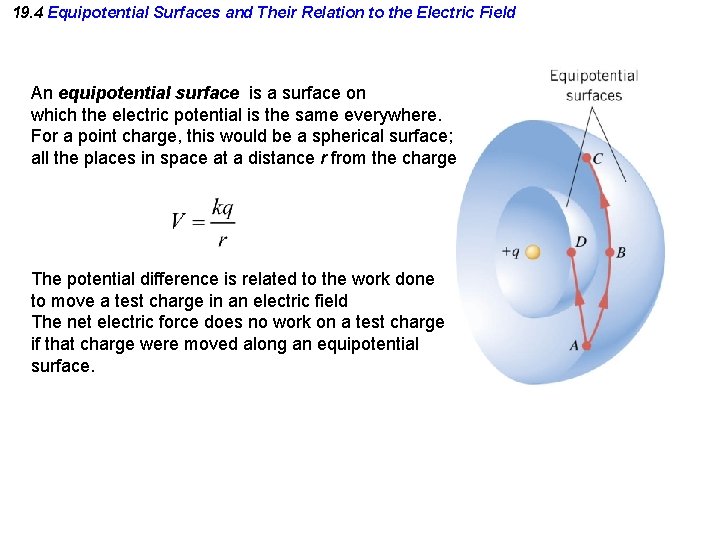
19. 4 Equipotential Surfaces and Their Relation to the Electric Field An equipotential surface is a surface on which the electric potential is the same everywhere. For a point charge, this would be a spherical surface; all the places in space at a distance r from the charge. The potential difference is related to the work done to move a test charge in an electric field The net electric force does no work on a test charge if that charge were moved along an equipotential surface.

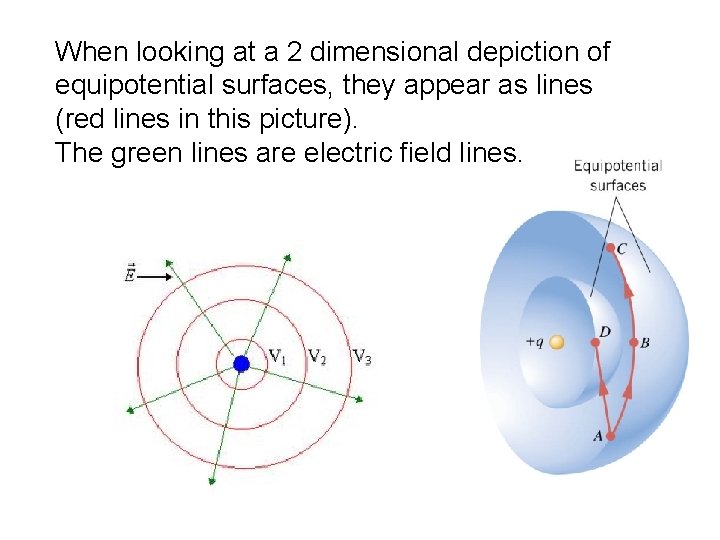
When looking at a 2 dimensional depiction of equipotential surfaces, they appear as lines (red lines in this picture). The green lines are electric field lines.

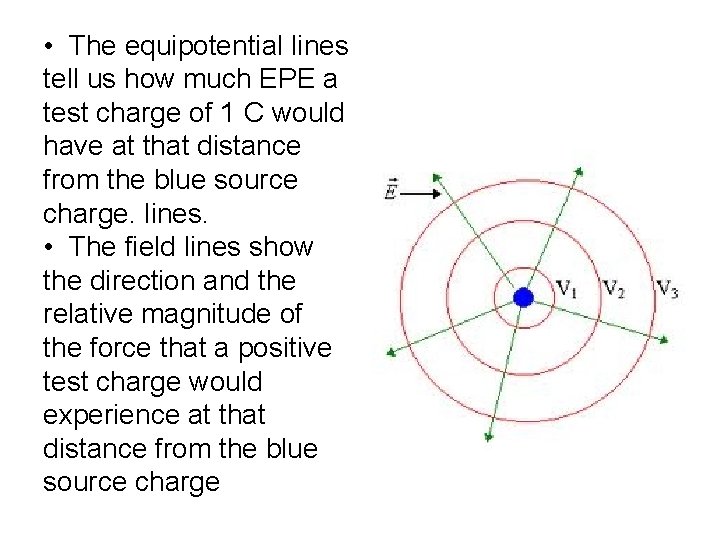
• The equipotential lines tell us how much EPE a test charge of 1 C would have at that distance from the blue source charge. lines. • The field lines show the direction and the relative magnitude of the force that a positive test charge would experience at that distance from the blue source charge

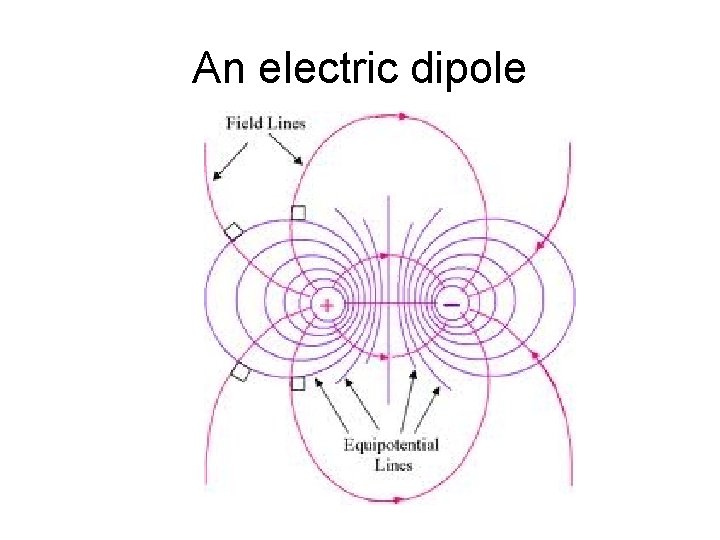
An electric dipole

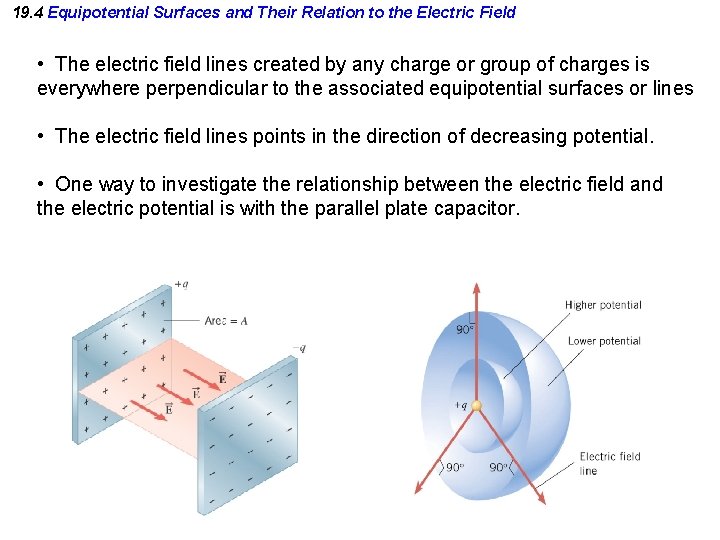
19. 4 Equipotential Surfaces and Their Relation to the Electric Field • The electric field lines created by any charge or group of charges is everywhere perpendicular to the associated equipotential surfaces or lines • The electric field lines points in the direction of decreasing potential. • One way to investigate the relationship between the electric field and the electric potential is with the parallel plate capacitor.

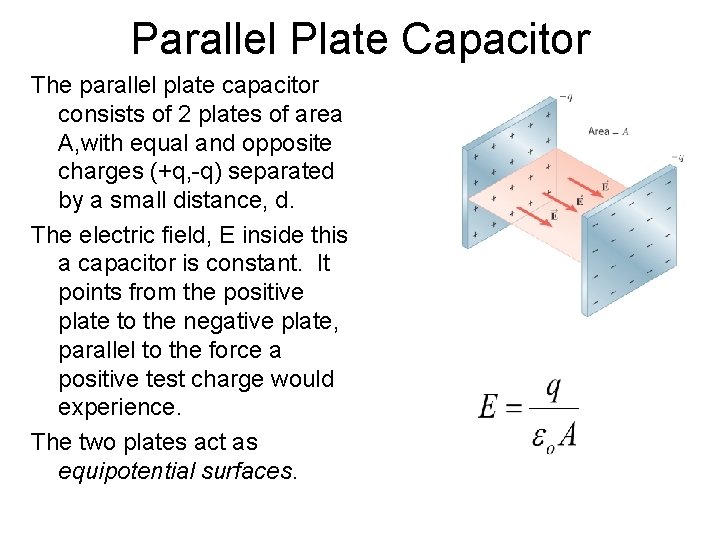
Parallel Plate Capacitor The parallel plate capacitor consists of 2 plates of area A, with equal and opposite charges (+q, -q) separated by a small distance, d. The electric field, E inside this a capacitor is constant. It points from the positive plate to the negative plate, parallel to the force a positive test charge would experience. The two plates act as equipotential surfaces.

Electric Potential of the Capacitor The electric potential is the same anywhere on each (imaginary) equipotential surface, and decreases in the direction of the electric field. A positive test charge would have the greatest EPE at the positive plate and the least EPE at the negative plate. The test charge would have the same EPE anywhere on an equipotential surface.

Relationship between Electric Field and Electric Potential of the Capacitor If the charge travels in the direction of the electric field, ∆V is negative, If the charge travels opposite to the electric field, ∆V is positive. This is the same for both negative and positive charge. E = - ∆V/ ∆s For the capacitor, we can simplify and write this as E = V/d where E is the magnitude of the electric field strength, V is the potential of the positive plate (with negative plate = 0 V) and d the plate spacing. The electric field E can be expressed in units of volts/meter (V/m).

Graphical representations of electric potential inside a capacitor • the green dashed contour lines represent equipotential surfaces. • Any point on one of these surfaces is at the same potential. • These surfaces are perpendicular to the direction of E. • E points in the direction of decreasing potential

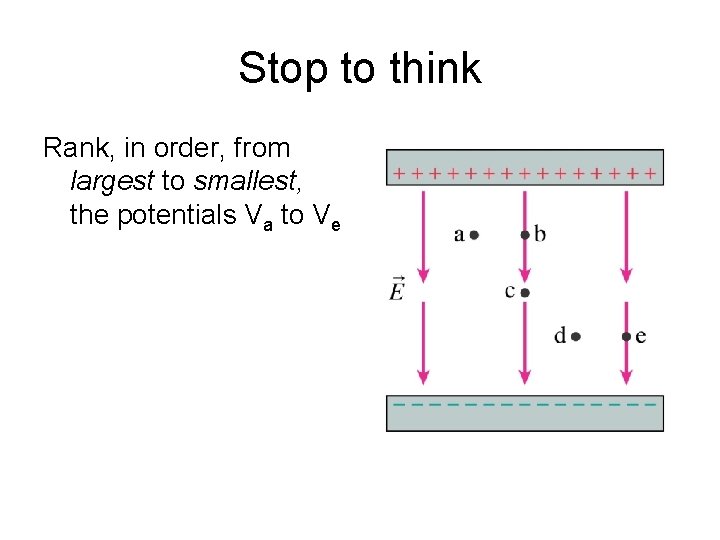
Stop to think Rank, in order, from largest to smallest, the potentials Va to Ve

EOC# 35 The inner and outer surfaces of a cell membrane carry a negative and a positive charge, respectively. Because of these charges, a potential difference of about 0. 070 V exists across the membrane. The thickness of the cell membrane is 8. 00 x 10 -9 m. What is the magnitude of the electric field in the membrane? outer + + + inner _ _ _ E

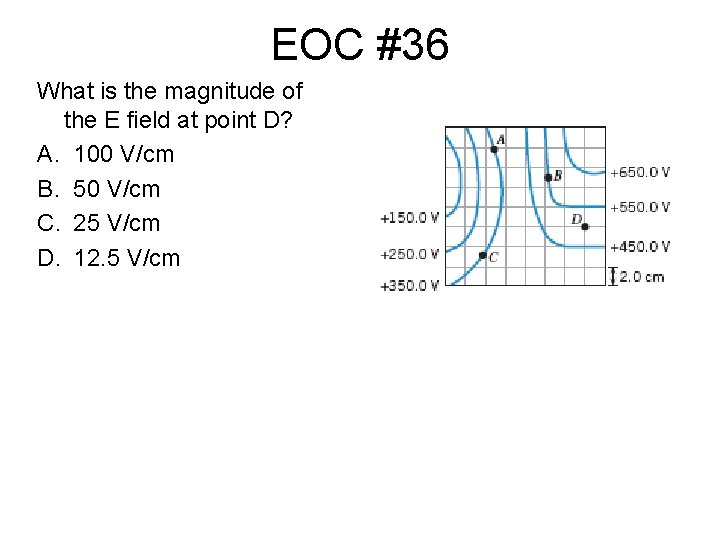
EOC #36 What is the magnitude of the E field at point D? A. 100 V/cm B. 50 V/cm C. 25 V/cm D. 12. 5 V/cm

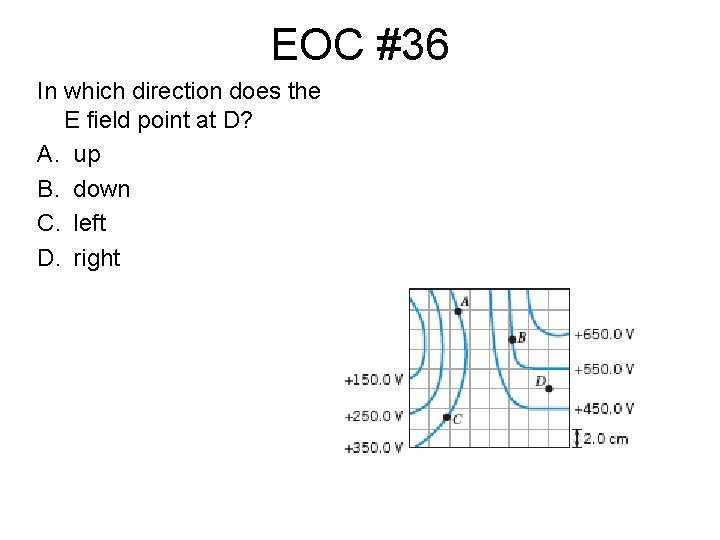
EOC #36 In which direction does the E field point at D? A. up B. down C. left D. right

Capacitors and Energy Storage • The capacitor stores energy, which it can release very rapidly. • The capacitor stores separated charges, which creates a potential difference (ΔV). Each of the charges has electric potential energy due to their position in the electric field of the capacitor.

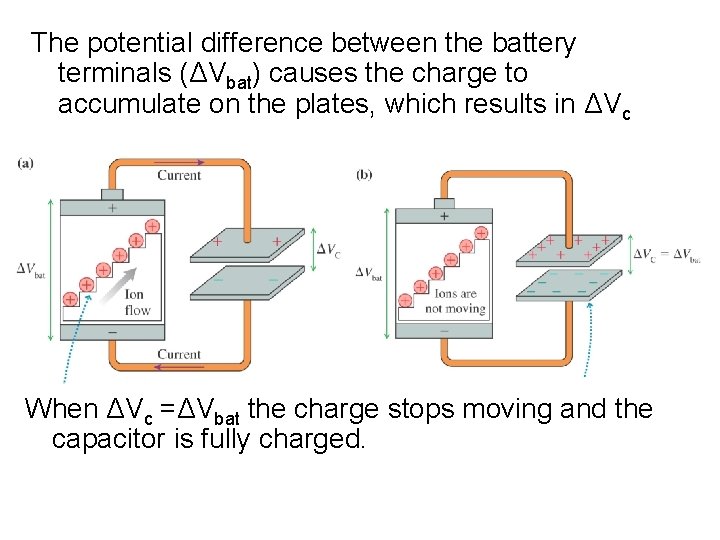
The potential difference between the battery terminals (ΔVbat) causes the charge to accumulate on the plates, which results in ΔVc When ΔVc =ΔVbat the charge stops moving and the capacitor is fully charged.

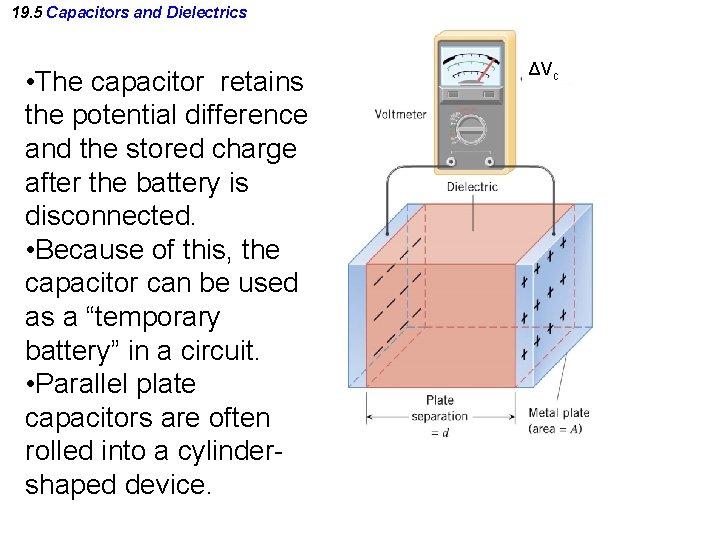
19. 5 Capacitors and Dielectrics • The capacitor retains the potential difference and the stored charge after the battery is disconnected. • Because of this, the capacitor can be used as a “temporary battery” in a circuit. • Parallel plate capacitors are often rolled into a cylindershaped device. ΔVc

The potential difference between the plates depends on the amount of charge separated: • But how much charge do I need to obtain a desired ∆V ? This depends on the geometry of the capacitor. • The area of the plate determines the charge density and is proportional to number of charges needed to maintain a given ∆V. • The distance between the plates separates the unlike charges; and is inversely proportional to the number of charges needed:

Given the relationship: The constant of proportionality is ε 0 : ε 0 = 8. 85 x 10 -12 C 2 /(N-m 2 ) And the whole quantity is defined as C, the capacitance of the capacitor:

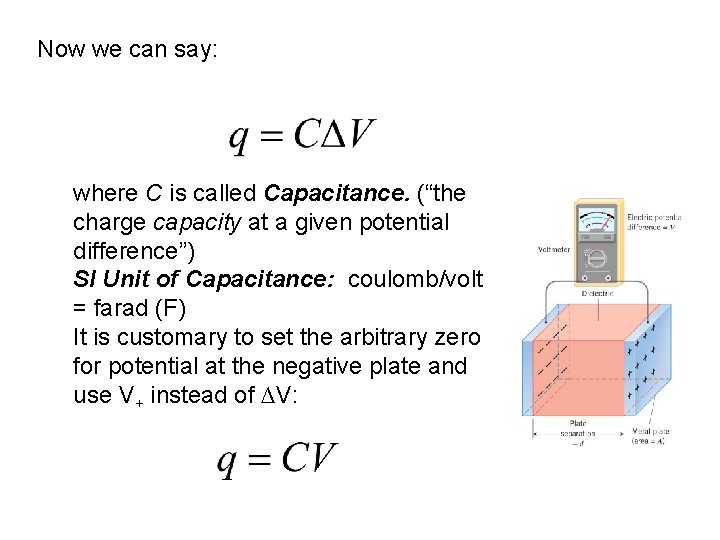
Now we can say: where C is called Capacitance. (“the charge capacity at a given potential difference”) SI Unit of Capacitance: coulomb/volt = farad (F) It is customary to set the arbitrary zero for potential at the negative plate and use V+ instead of ∆V:

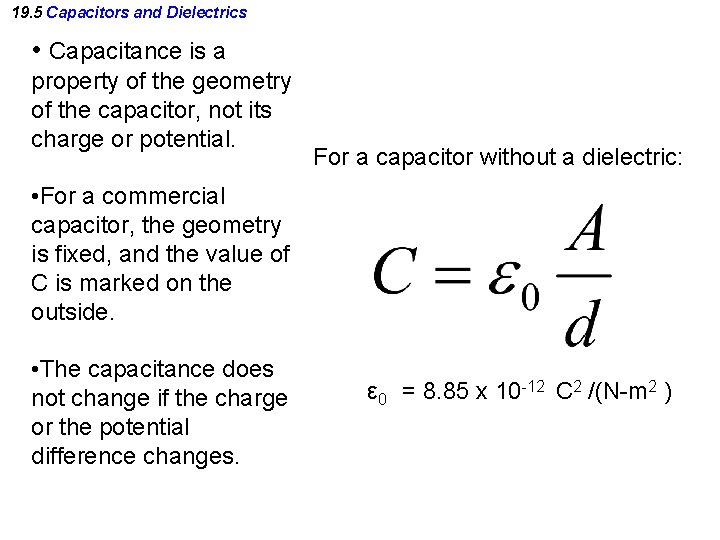
19. 5 Capacitors and Dielectrics • Capacitance is a property of the geometry of the capacitor, not its charge or potential. For a capacitor without a dielectric: • For a commercial capacitor, the geometry is fixed, and the value of C is marked on the outside. • The capacitance does not change if the charge or the potential difference changes. ε 0 = 8. 85 x 10 -12 C 2 /(N-m 2 )

A parallel plate capacitor is connected to a battery that maintains a constant potential difference between the plates. If the plates are pulled away from each other, doubling the separation (d), by what factor does the amount of charge on the plates change ? A. B. C. D. No change, the separation distance is not a factor By a factor of 2 (doubles). By a factor of one half Impossible to say without knowing the area and original separation distance of the capacitor.

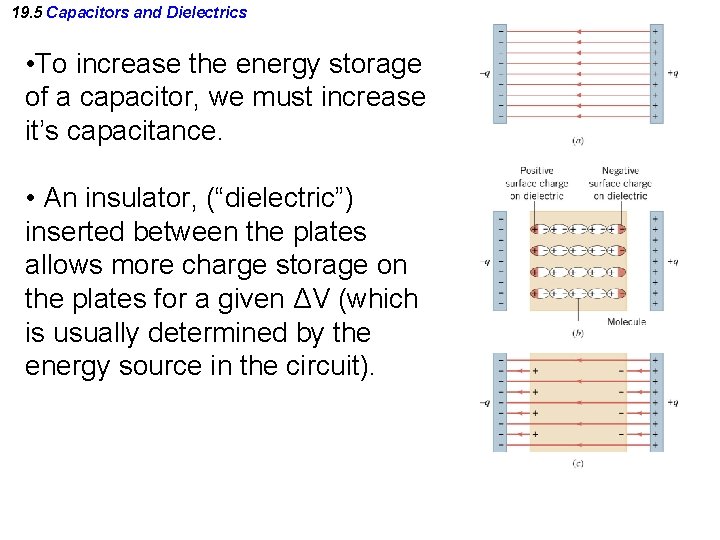
19. 5 Capacitors and Dielectrics • To increase the energy storage of a capacitor, we must increase it’s capacitance. • An insulator, (“dielectric”) inserted between the plates allows more charge storage on the plates for a given ΔV (which is usually determined by the energy source in the circuit).

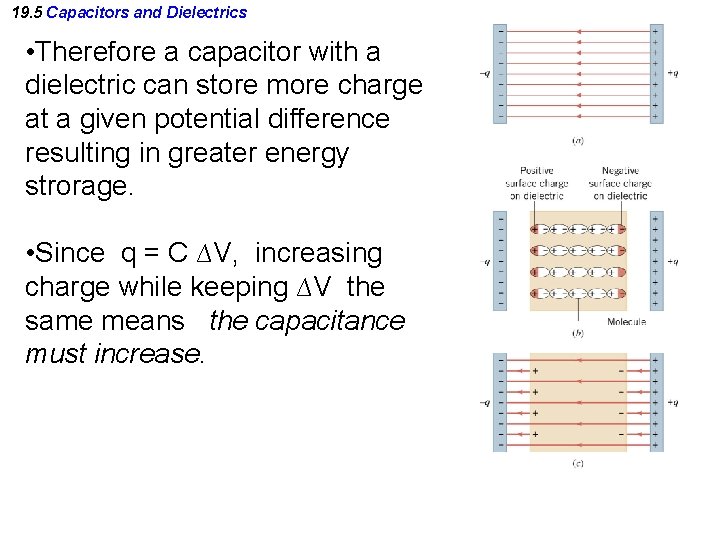
19. 5 Capacitors and Dielectrics • Therefore a capacitor with a dielectric can store more charge at a given potential difference resulting in greater energy strorage. • Since q = C ∆V, increasing charge while keeping ∆V the same means the capacitance must increase.

THE CAPACITANCE OF A PARALLEL PLATE CAPACITOR WITH A DIELECTRIC Where k is the dielectric constant of the material (found in a table in most texts), and C 0 is the capacitance without dielectric. ε 0 = 8. 85 x 10 -12 C 2/Nm 2

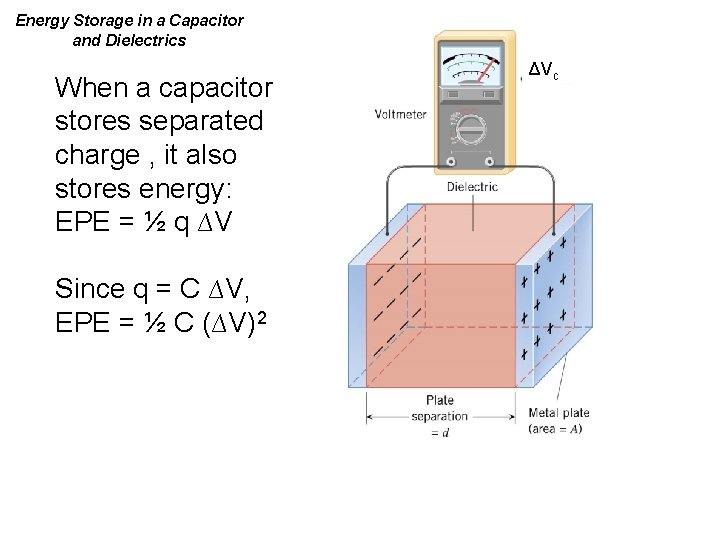
Energy Storage in a Capacitor and Dielectrics When a capacitor stores separated charge , it also stores energy: EPE = ½ q ∆V Since q = C ∆V, EPE = ½ C (∆V)2 ΔVc

Remember power? What is the potential difference between the plates of a 3. 2 -F capacitor that stores sufficient energy to operate a 83 -W light bulb for three minutes? Recall that power (in units of Watts) is energy used per unit time (SI units are J/s)

Remember power? What is the potential difference between the plates of a 3. 2 -F capacitor that stores sufficient energy to operate a 83 -W light bulb for three minutes? Ans: 96. 6 V

Which two, or more, of the following actions would increase the energy stored in a parallel plate capacitor when a constant potential difference is applied across the plates (i. e. battery remains attached)? 1. increase the area of the plates 2. decrease the area of the plates 3. increase the separation between the plates 4. decrease the separation between the plates 5. insert a dielectric between the plates A. 2, 3, 5 B. 1, 4, 5 C. 1, 3 D. 2, 4

Energy storage with a dielectric • An empty capacitor is capable of storing 1. 0 x 10 -4 J of energy when connected to a certain battery. If the distance between the plates is halved and then filled with a dielectric (κ = 2. 5), how much energy could this modified capacitor store when connected to the same battery?

Energy storage with a dielectric • An empty capacitor is capable of storing 1. 0 x 10 -4 J of energy when connected to a certain battery. If the distance between the plates is halved and then filled with a dielectric (κ = 2. 5), how much energy could this modified capacitor store when connected to the same battery? • Ans: 5 E 0 where E 0 is 1. 0 x 10 -4 J