Function Generators FUNCTION GENERATORS Function generators which are

Function Generators

FUNCTION GENERATORS Function generators, which are very important and versatile instruments. provide a variety of output waveforms over a wide frequency range. The most common output waveforms are sine, square, triangular, ramp. and pulse. The frequency range generally extends from a fraction of a hertz to at least several hundred kilohertz.

Since a function generator provides sine, square, and triangular wave outputs, any of these may be the primary waveform generated by the instrument. This primary waveform can then be applied to the proper circuitry to generate the remaining waveforms.

For example, the primary waveform may be a sine wave generated with the RC or LC oscillator circuit. However, because of difficulties with amplitude and frequency stability, particularly at very low frequencies, oscillators with a sine wave as the primary output are generally not used.

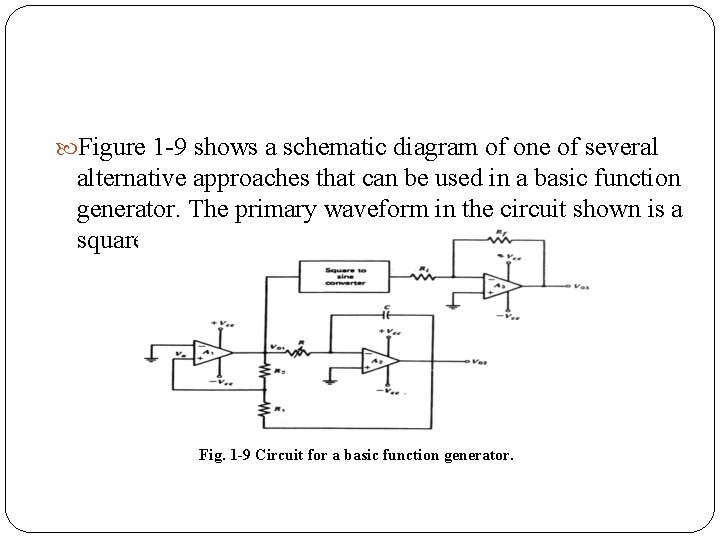
Figure 1 9 shows a schematic diagram of one of several alternative approaches that can be used in a basic function generator. The primary waveform in the circuit shown is a square wave. Fig. 1 -9 Circuit for a basic function generator.

This waveform is chosen because some circuits generating square waves are simpler and offer significantly better amplitude and frequency stability than do circuits generating sine waves. The first stage, A 1, which is a voltage comparator, generates a square wave output. The output of A 1 is driven to saturation; therefore, the square wave is either at + Vcc or Vcc.

The second stage, A 2 is an integrator which generates a triangular output. The square wave is applied to a square to sine wave converter that filters out the odd harmonics making u the square wave while passing on only the fundamental sine wave. The operation of the circuit can be analyzed by starting at the output of the comparator, which la at either +Vcc or Vcc. Consider V 01 to be at –Vcc.

The voltage V 01 will remain at Vcc until the voltage at the inverting input of A, exceeds the voltage at the noninverting input, which in this case is at zero volts. The noninverting input voltage. Vx, is due, in par, to the voltage V 01 and, in part, to the voltage V 02, according to the expression (1 24)

The output V 01 changes states when Vx = 0; therefore. we can say (1 -25) which simplifies to (1 -26)

From Eq. 1 26 we can determine the maximum amplitude of the triangular output. V 02, which is expressed as (1 27)

When the output voltage V 02 reaches the amplitude given by Eq. 1 27. the output of the comparator changes stars and the triangular wave begins to decrease linearly. Since the output is symmetrical about by Eq. 1 27 also expresses the minimum value of V 02 at which switching occurs.

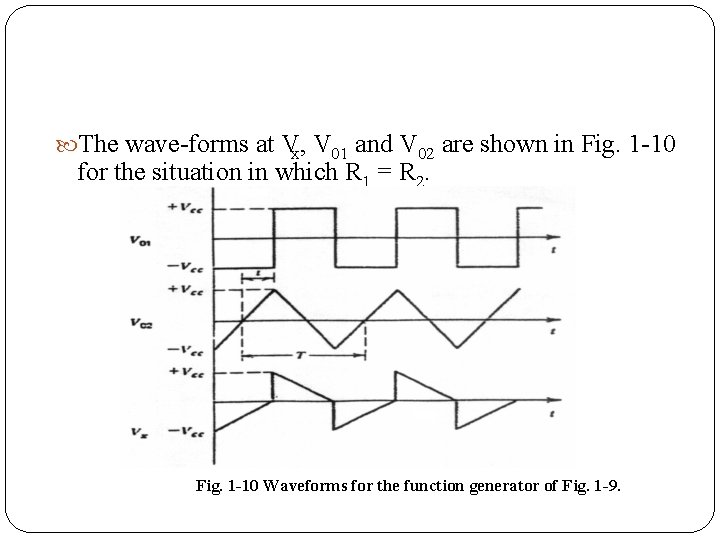
The wave forms at Vx, V 01 and V 02 are shown in Fig. 1 10 for the situation in which R 1 = R 2. Fig. 1 -10 Waveforms for the function generator of Fig. 1 -9.

The frequency of the circuit is controlled by the RC time constant of the integrator. To obtain an expression for the frequency. we begin with the expression relating capacitor current. charge, and time of change: (1 28) The rate of charge of the capacitor is (1 29)

which can be written as (1 30) As the capacitor charges. the relationship between charge, capacitance, and voltage across the capacitor plates is (1 31)

Substituting Eq. 1 31 into Eq. 1 30 yields (1 32) Since the input resistance of the operational amplifier is very high. the current through resistor R is approximately equal to the charging current of the capacitor. Therefore, we can write (1 33)

In addition, since the voltage gain of the operational amplifier is very high. the voltage at the input to the amplifier is very nearly zero. Therefore (1 34) Substituting Eq. 1 34 into Eq. 1 33. we obtain (1 35)

Integrating both sides of Eq. 1 35, we obtain (1 36) Substituting Eq. 1 27 into Eq. 1 36 yields (1 37)

Since V 01 =Vcc. Eq. 1 37 simplifies to (1 38) The development of Eq. 1 38 began with Eq. 1 28. which allows us to compute the charge on a capacitor after a period of time t. Equation 1 28 is valid only if the initial charge and, therefore. the initial voltages on the capacitor are zero. Therefore, the time t in Eq. 1 38 is the time for the capacitor to charge from 0 V until switching occurs. which is at one fourth cycle as shown in Fig. 1 10.

Therefore, the time t in Eq. 1 38 is the time for the capacitor to charge from 0 V until switching occurs. which is at one fourth cycle as shown in Fig. 1 10. Since Eq. 1 38 becomes (1 39) The frequency which is the reciprocal of the period, is now expressed as (1 40)

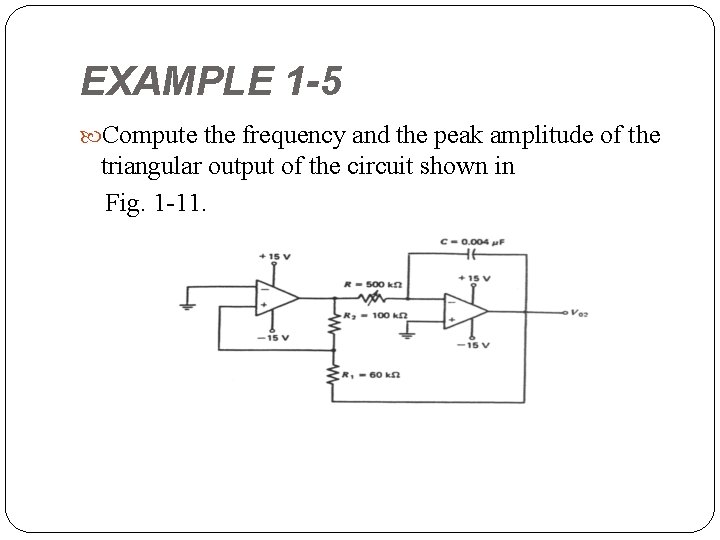
EXAMPLE 1 -5 Compute the frequency and the peak amplitude of the triangular output of the circuit shown in Fig. 1 11 Function generator for Example 1 5.

The amplitude of the triangular waveform can be computed from Eq. 1 27 a

Figure 10 12 shows an Exact Electronic Model 528 function generator. Fig. 1 12 Laboratory quality function generator. (Courtesy Exact Electronics. )

This laboratory – quality instrument generates sine, square, triangle, ramp, and pulse waveforms over the frequency range from 03. 001 Hz to 20 MHz. The output voltage is 30 V peak to peak in an open circuit and 15 V peak to peak across a 50 load.