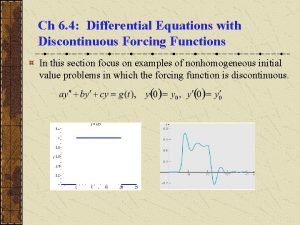
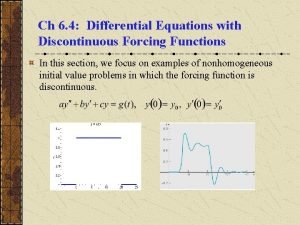
Chapter 2 SecondOrder Differential Equations 2 1 Preliminary



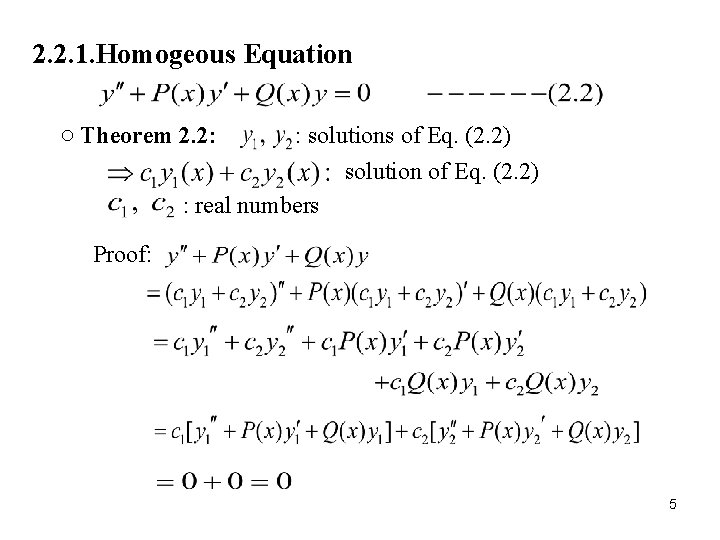


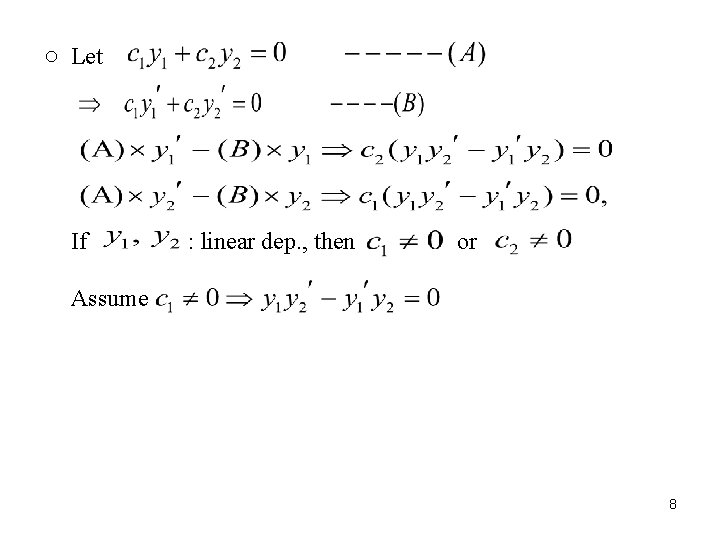









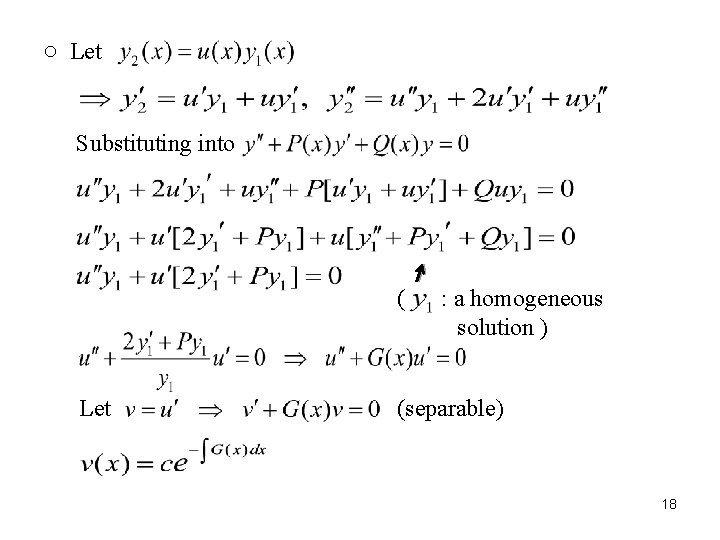
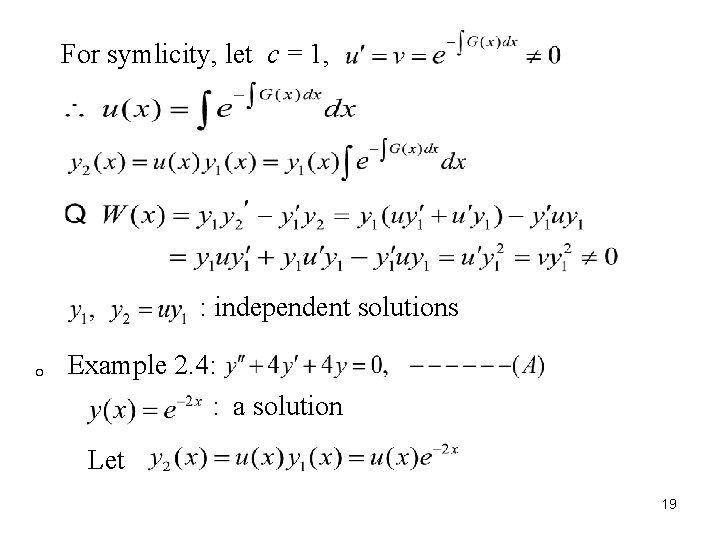




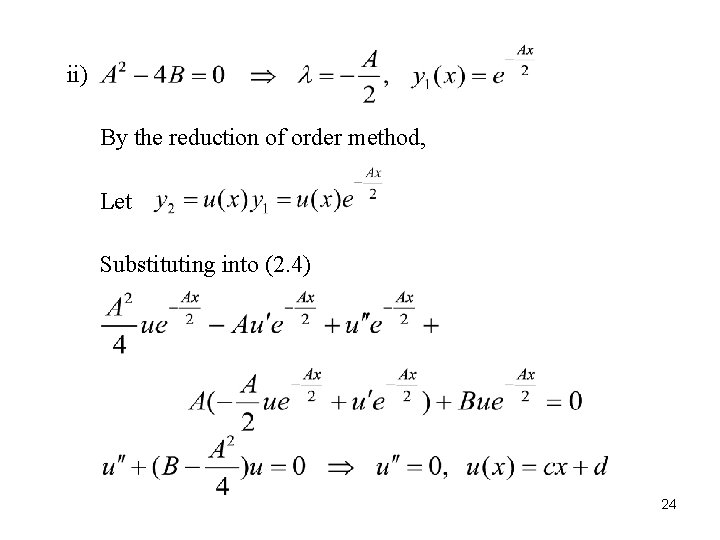




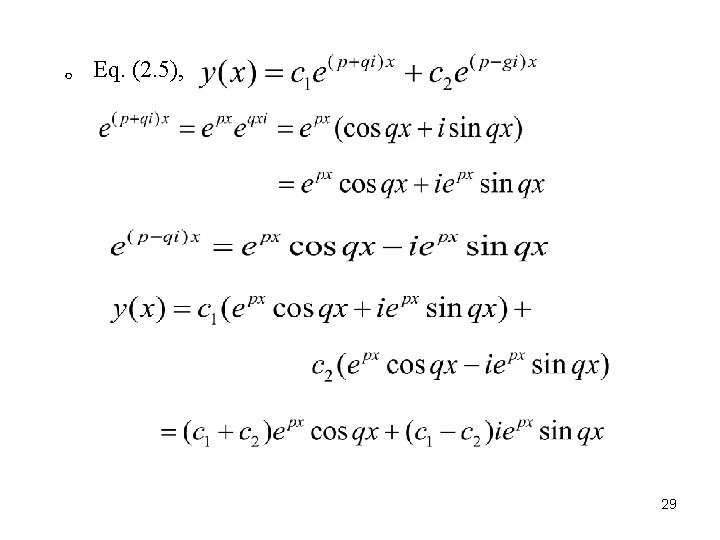






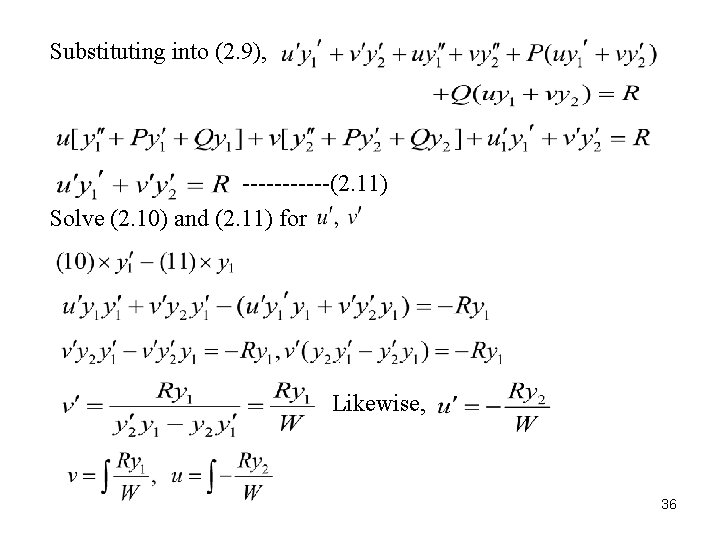


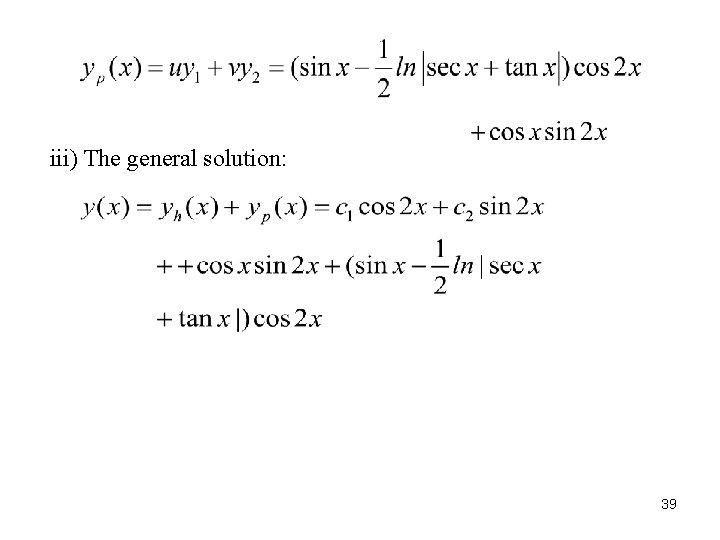









- Slides: 48

Chapter 2: Second-Order Differential Equations 2. 1. Preliminary Concepts ○ Second-order differential equation e. g. , Solution: A function satisfies , (I : an interval) 1

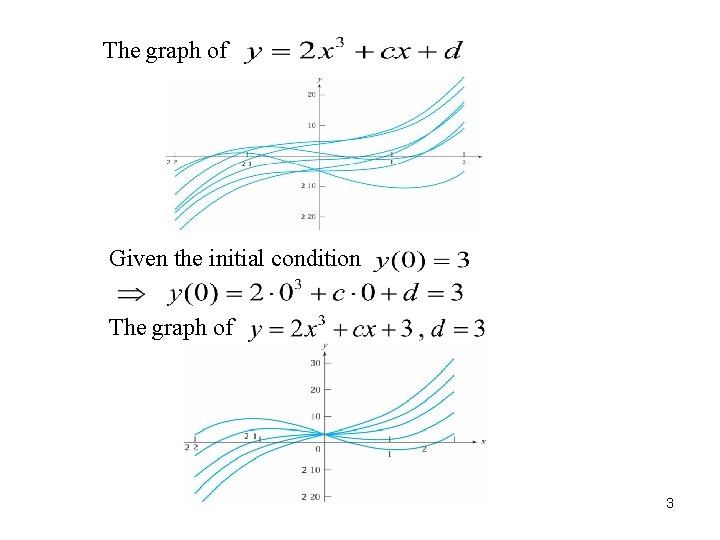
○ Linear second-order differential equation Nonlinear: e. g. , 2. 2. Theory of Solution ○ Consider y contains two parameters c and d 2

The graph of Given the initial condition The graph of 3

Given another initial condition The graph of ◎ The initial value problem: ○ Theorem 2. 1: : continuous on I, has a unique solution 4
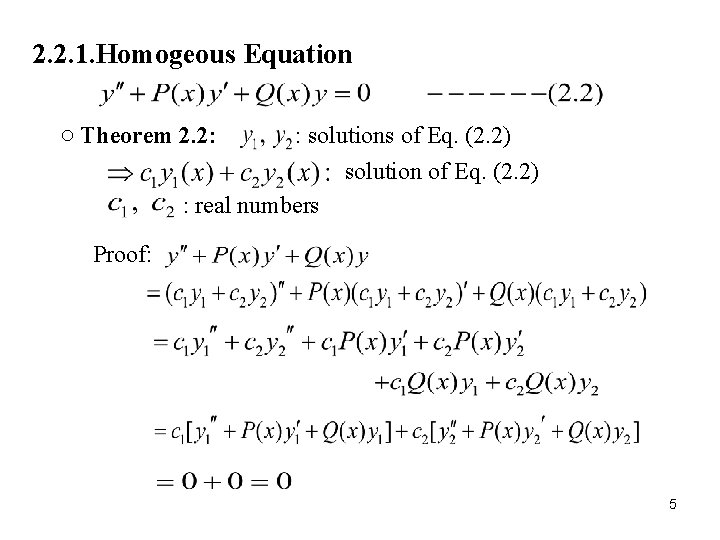
2. 2. 1. Homogeous Equation ○ Theorem 2. 2: : solutions of Eq. (2. 2) solution of Eq. (2. 2) : real numbers Proof: 5

※ Two solutions are linearly independent. Their linear combination provides an infinity of new solutions ○ Definition 2. 1: f , g : linearly dependent If s. t. or ; otherwise f , g : linearly independent In other words, f and g are linearly dependent only if for 6

○ Wronskian test -- Test whether two solutions of a homogeneous differential equation are linearly independent Define: Wronskian of solutions to be the 2 by 2 determinant 7
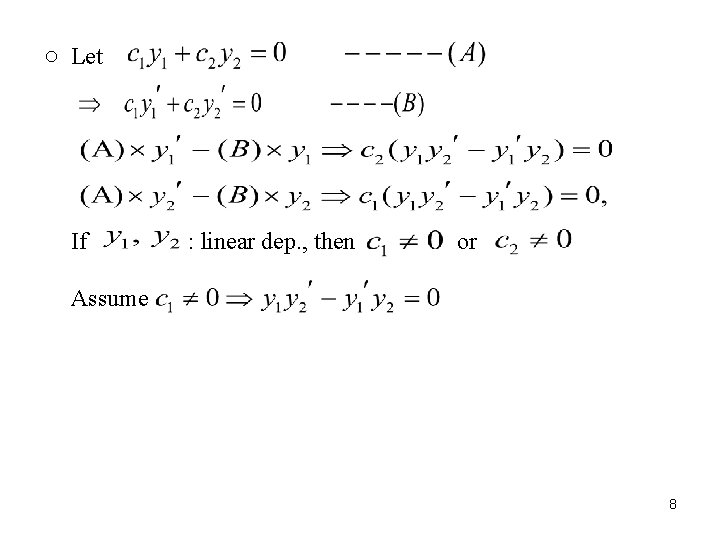
○ Let If : linear dep. , then or Assume 8

○ Theorem 2. 3: 1) Either 2) or : linearly independent iff Proof (2): (i) (if : linear indep. (P), then (Q) then if : linear dep. ( ( Q) , P) ) : linear dep. 9

(ii) (if if ( P)) (P), then : linear indep. (Q) : linear dep. ( Q), then : linear dep. , ※ Test at just one point of I to determine linear dependency of the solutions 10

。 Example 2. 2: are solutions of : linearly independent 11

。 Example 2. 3: Solve by a power series method The Wronskian of at nonzero x would be difficult to evaluate, but at x = 0 are linearly independent 12

◎ Find all solutions ○ Definition 2. 2: 1. : linearly independent : fundamental set of solutions 2. : general solution : constant ○ Theorem 2. 4: : linearly independent solutions on I Any solution is a linear combination of 13

Proof: Let be a solution. Show Let Then, s. t. and is the unique solution on I of the initial value problem 14

2. 2. 2. Nonhomogeneous Equation ○ Theorem 2. 5: : linearly independent homogeneous solutions of : a nonhomogeneous solution of any solution has the form 15

Proof: Given , solutions : a homogenous solution of : linearly independent homogenous solutions (Theorem 2. 4) 16

○ Steps: 1. Find the general homogeneous solutions of 2. Find any nonhomogeneous solution of 3. The general solution of is 2. 3. Reduction of Order -- A method for finding the second independent homogeneous solution when given the first one 17
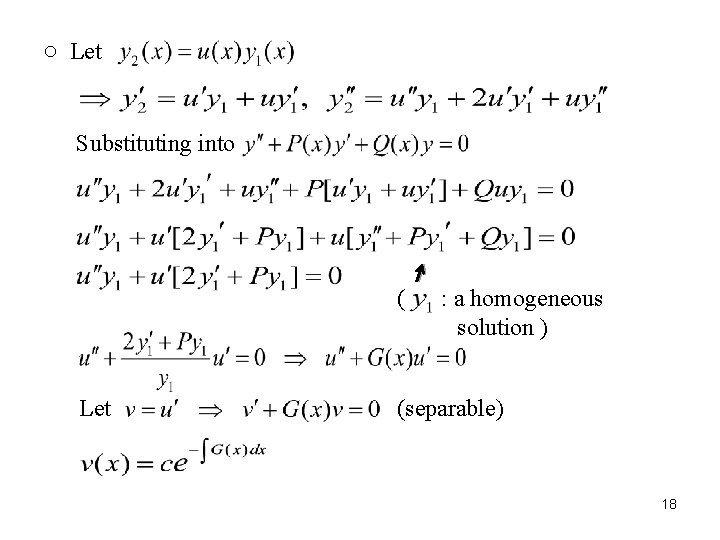
○ Let Substituting into ( Let : a homogeneous solution ) (separable) 18
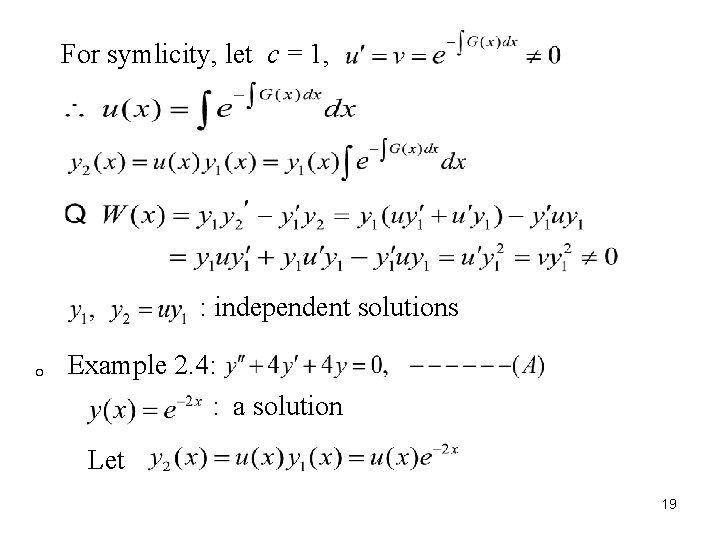
For symlicity, let c = 1, : independent solutions 。 Example 2. 4: : a solution Let 19

Substituting into (A), For simplicity, take c = 1, d = 0 : independent The general solution: 20

2. 4. Constant Coefficient Homogeneous A, B : numbers ----- (2. 4) The derivative of is a constant (i. e. , ) multiple of Constant multiples of derivatives of y , which has form , must sum to 0 for (2, 4) ○ Let Substituting into (2, 4), (characteristic equation) 21

i) Solutions : : linearly independent The general solution: 22

。 Example 2. 6: Let , Then Substituting into (A), The characteristic equation: The general solution: 23
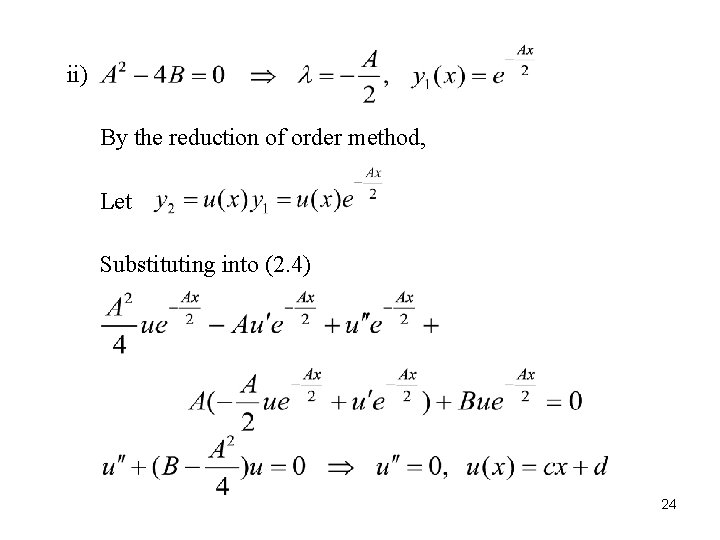
ii) By the reduction of order method, Let Substituting into (2. 4) 24

Choose : linearly independent The general sol. : 。 Example 2. 7: Characteristic eq. : The repeated root: The general solution: 25

iii) Let The general sol. : 26

。 Example 2. 8: Characteristic equation: Roots: The general solution: ○ Find the real-valued general solution 。 Euler’s formula: 27

Maclaurin expansions: 28
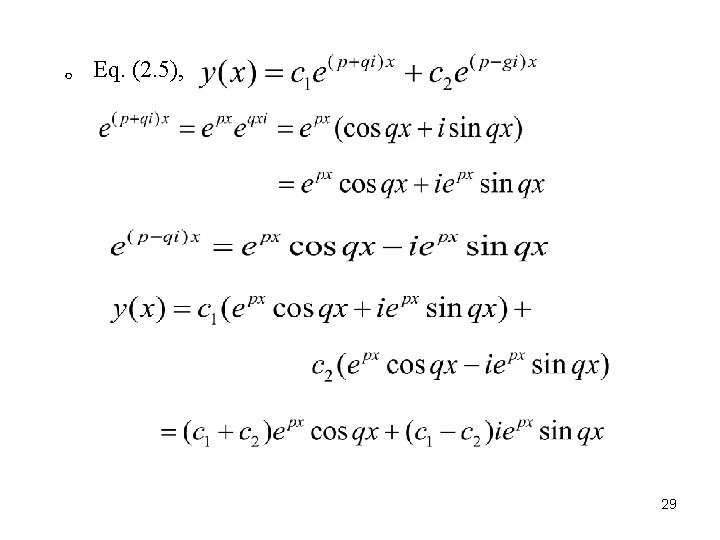
。 Eq. (2. 5), 29

Find any two independent solutions Take The general sol. : 30

2. 5. Euler’s Equation , A , B : constants -----(2. 7) Transform (2. 7) to a constant coefficient equation by letting 31

Substituting into Eq. (2. 7), i. e. , ----(2. 8) Steps: (1) Solve (2) Substitute (3) Obtain 32

。 Example 2. 11: ------(A) -------(B) (i) Let Substituting into (A) Characteristic equation: Roots: General solution: 33

○ Solutions of constant coefficient linear equation have the forms: Solutions of Euler’s equation have the forms: 34

2. 6. Nonhomogeneous Linear Equation ------(2. 9) The general solution: ◎ Two methods for finding (1) Variation of parameters -- Replace with homogeneous solution in the general Let Assume ------(2. 10) Compute 35
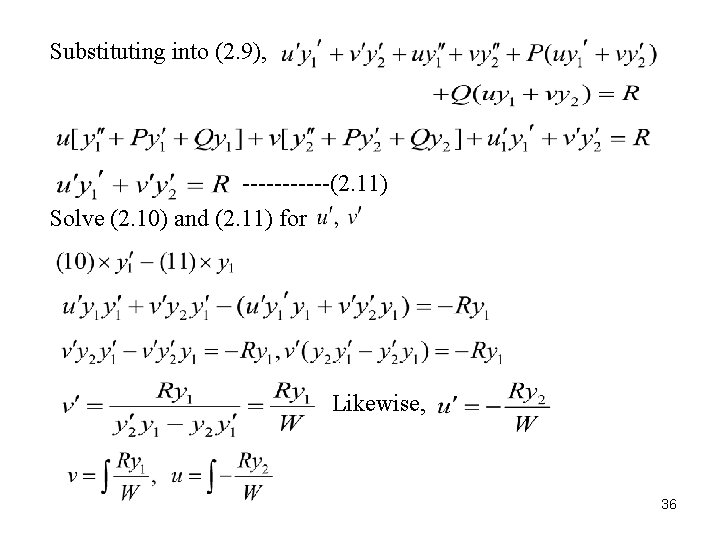
Substituting into (2. 9), ------(2. 11) Solve (2. 10) and (2. 11) for . Likewise, 36

。 Example 2. 15: ------(A) i) General homogeneous solution : Let. Substitute into (A) The characteristic equation: Complex solutions: Real solutions: : independent 37

ii) Nonhomogeneous solution Let 38
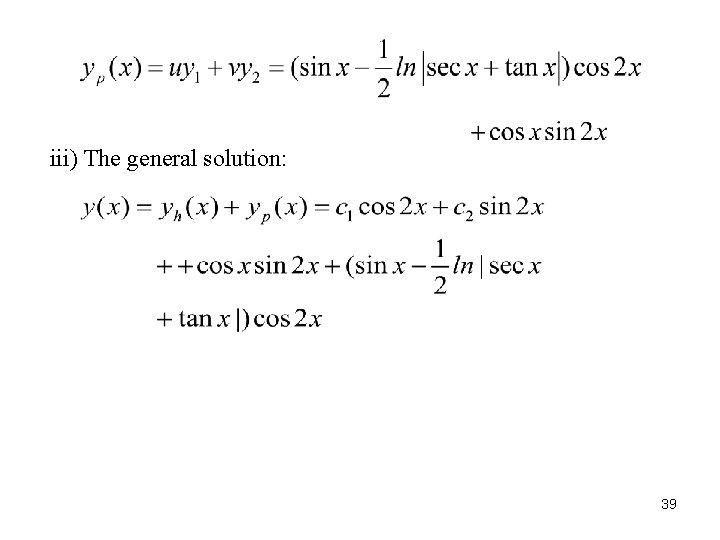
iii) The general solution: 39

(2) Undetermined coefficients Apply to A, B: constants Guess the form of e. g. from that of R : a polynomial Try a polynomial for : an exponential for Try an exponential for 40

。 Example 2. 19: ---(A) It’s derivatives can be multiples of or Try Compute Substituting into (A), 41

: linearly independent and The homogeneous solutions: The general solution: 42

。 Example 2. 20: ------(A) , try Substituting into (A), * This is because the guessed contains a homogeneous solution Strategy: If a homogeneous solution appears in any term of , multiply this term by x. If the modified term still occurs in a homogeneous solution, multiply by x again 43

Try Substituting into (A), 44

○ Steps of undetermined coefficients: (1) Find homogeneous solutions (2) From R(x), guess the form of If a homogeneous solution appears in any term of , multiply this term by x. If the modified term still occurs in a homogeneous solution, multiply by x again (3) Substitute the resultant into and solve for its coefficients 45

○ Guess Let from : a given polynomial , : polynomials with unknown coefficients Guessed 46

2. 6. 3. Superposition Let be a solution of is a solution of (A) 47

。 Example 2. 25: The general solution: where homogeneous solutions 48
 Differential equations chapter 1
Differential equations chapter 1 Differential equations projects
Differential equations projects Bernoulli differential equation ppt
Bernoulli differential equation ppt Differential equations in computer science
Differential equations in computer science Cengage differential equations
Cengage differential equations Ordinary differential equations
Ordinary differential equations Euler midpoint method
Euler midpoint method Differential calculus
Differential calculus Differential equations meaning
Differential equations meaning Integrating factor of differential equation
Integrating factor of differential equation Characteristics method partial differential equations
Characteristics method partial differential equations What is a first order equation
What is a first order equation Integrating factor of differential equation
Integrating factor of differential equation Differential equations formula
Differential equations formula Cengage differential equations
Cengage differential equations Natural solution
Natural solution Second order differential equation
Second order differential equation Solving 1st order differential equations
Solving 1st order differential equations Classifying differential equations
Classifying differential equations Traffic flow differential equations
Traffic flow differential equations 1st order derivative formula
1st order derivative formula Implicit euler method
Implicit euler method First order linear equation
First order linear equation Variable separable
Variable separable Slidetodoc
Slidetodoc Differential equations
Differential equations Differential equations with discontinuous forcing functions
Differential equations with discontinuous forcing functions Bernoulli equation differential equations examples
Bernoulli equation differential equations examples Parachute problem
Parachute problem Non homogeneous differential equation definition
Non homogeneous differential equation definition Differential equations and linear algebra strang
Differential equations and linear algebra strang Growth and decay differential equations
Growth and decay differential equations Dennis g zill differential equations solutions
Dennis g zill differential equations solutions Stewart differential equations
Stewart differential equations Hertz
Hertz Mechanical and electrical vibrations
Mechanical and electrical vibrations Undetermined coefficients annihilator approach
Undetermined coefficients annihilator approach Ordinary differential equations example
Ordinary differential equations example Ordinary differential equations example
Ordinary differential equations example Integration of partial differential equation
Integration of partial differential equation Higher order linear differential equations
Higher order linear differential equations Define homogeneous differential equation
Define homogeneous differential equation Mixing problems differential equations
Mixing problems differential equations Derivation of maxwell's equations in differential form
Derivation of maxwell's equations in differential form Differential equations with discontinuous forcing functions
Differential equations with discontinuous forcing functions Derivation of maxwell's equations in differential form
Derivation of maxwell's equations in differential form Partial differential equation solution
Partial differential equation solution Differential equations summary
Differential equations summary Piecewise differential equation
Piecewise differential equation