SecondOrder Differential Equations 2 1 Preliminary Concepts Secondorder







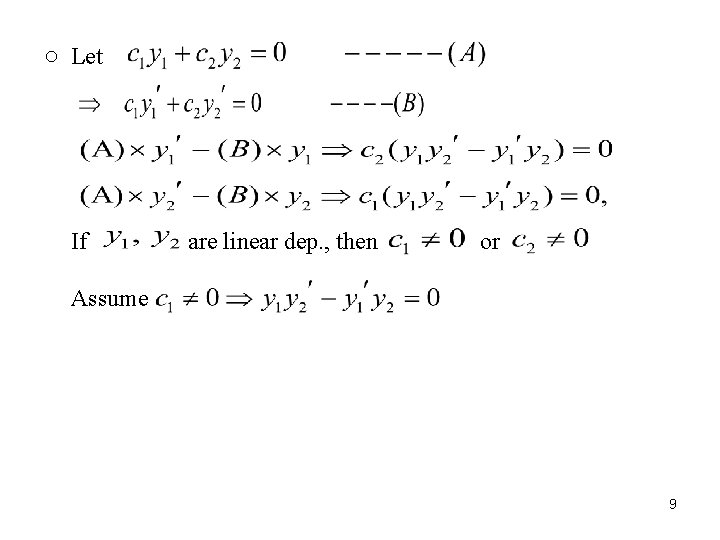




![Fundamental solution set • A pair of solutions [y 1, y 2] of L[y] Fundamental solution set • A pair of solutions [y 1, y 2] of L[y]](https://slidetodoc.com/presentation_image_h2/9e0969b551e01176480522e9e1de2171/image-14.jpg)





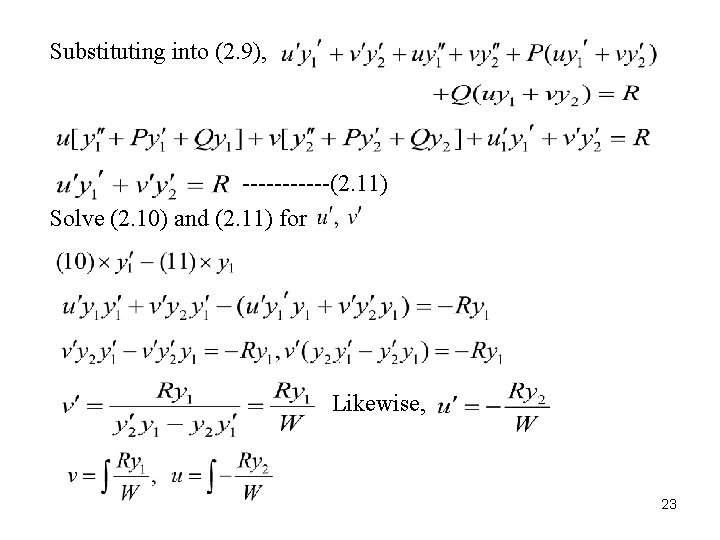


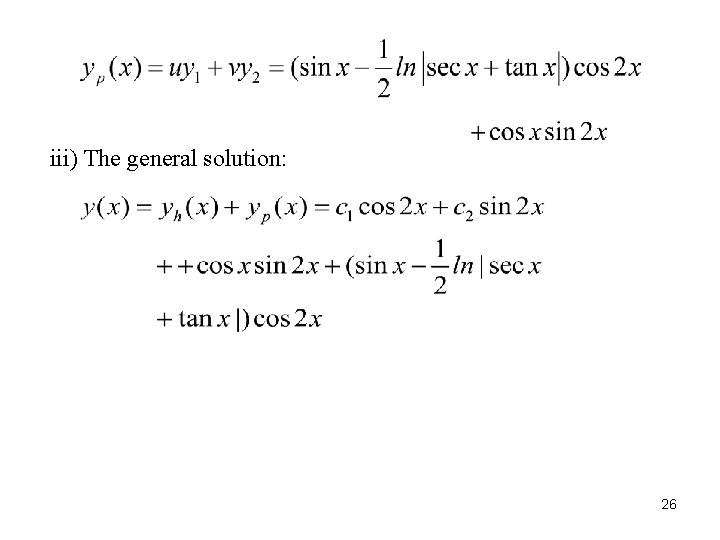









- Slides: 35

Second-Order Differential Equations 2. 1. Preliminary Concepts ○ Second-order differential equation e. g. , Solution: A function satisfies , (I : an interval) 1

○ Linear second-order differential equation Nonlinear: e. g. , 2. 2. Theories of Solution ○ Consider y contains two parameters c and d 2

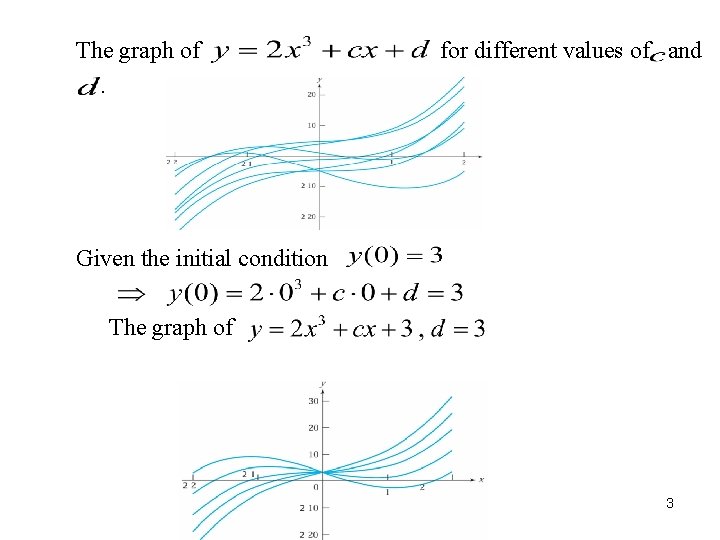
The graph of. for different values of and Given the initial condition The graph of 3

Given another initial condition The graph of ◎ The initial value problem (I. V. P): 4

Existence and Uniqueness of 1 st order equation Theorem 1 • Suppose P(x) and Q(x) are continuous on the interval (a, b) that contains the point x 0. Then the initial value problem: • y + P(x)y = Q(x), y(x 0)=y 0 for any given y 0 has a unique solution on (a, b). 5 5

Existence and Uniqueness of 2 nd order equation • Theorem 2. Let p(x), q(x) and g(x) be continuous on an interval (a, b), and x 0 (a, b). Then the I. V. P. 6 6

※ Linear independent solutions Two solutions are linearly independent if their linear combination provides an infinity of new solutions ○ Definition 2. 1: f , g : linearly dependent If s. t. or ; otherwise f , g : linearly independent In other words, f and g are linearly dependent only if for 7

Wronskian ○ Wronskian test whether two solutions of a homogeneous differential equation are linearly independent Define: Wronskian of solutions is the 2 by 2 determinant 8
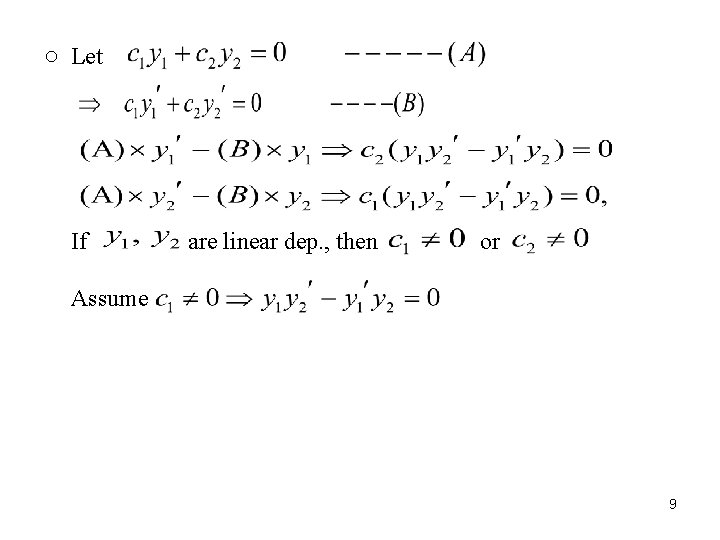
○ Let If are linear dep. , then or Assume 9

○ Theorem 2. 3: 1) Either 2) or are linearly independent iff Proof (2): (i) if are linearly independent, then if then , are linearly dependent. 10

(ii) Conversely, if , then independent. if linear dep. then are linearly : linear dep. , ※ Test at just one point of I to determine linear dependency of the solutions 11

。 Example 2. 2: are solutions of : linearly independent 12

。 Example 2. 3: Solve by a power series method The Wronskian of at nonzero x would be difficult to evaluate, but at x = 0 are linearly independent 13
![Fundamental solution set A pair of solutions y 1 y 2 of Ly Fundamental solution set • A pair of solutions [y 1, y 2] of L[y]](https://slidetodoc.com/presentation_image_h2/9e0969b551e01176480522e9e1de2171/image-14.jpg)
Fundamental solution set • A pair of solutions [y 1, y 2] of L[y] = 0, on (a, b) where L[y] = y +py +qy is called a fundamental solution set, if W[y 1, y 2](x 0) 0 for some x 0 (a, b). A simple example: Consider • L[y] = y +9 y. It is easily checked that y 1 = cos 3 x and y 2 = sin 3 x are solutions of L[y] = 0. Since the corresponding Wronskian W[y 1, y 2](x) = 3 0 , thus {cos 3 x, sin 3 x} forms a fundamental solution set to the homogenenous eq: y + 9 y = 0. We see that any linear combination c 1 y 1 + c 2 y 2 also satisfies L[y] = 0. This is known as a general solution 14

Homogeneous 2 nd order o. d. e with constant coefficients The general formula for such equation is To solve this equation we assume the solution in the form of exponential function: If then and the equation will change into after dividing by the eλx we obtain We obtained a quadratic characteristic equation. The roots are 15

There exist three types of solutions according to the discriminant D 1) If D>0, the roots λ 1, λ 2 are real and distinct 2) If D=0, the roots are real and identical λ 12 =λ 3) If D<0, the roots are complex conjugate λ 1, λ 2 where α and ω are real and imaginary parts of the root 16

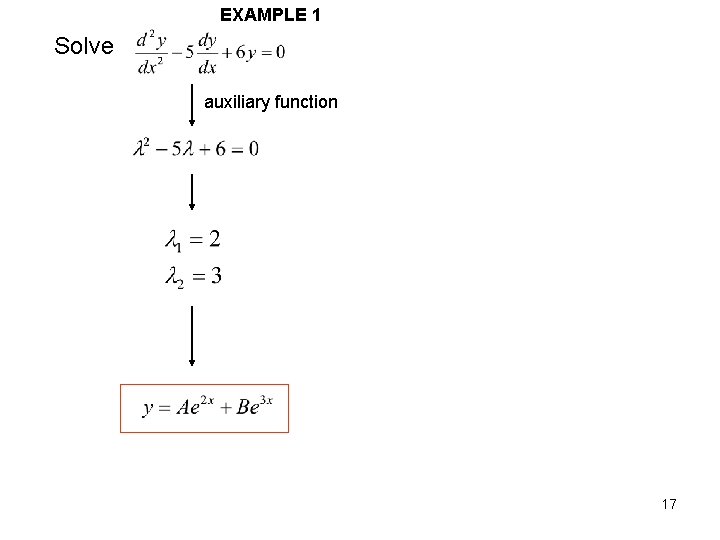
EXAMPLE 1 Solve auxiliary function 17

EXAMPLE 2 Solve auxiliary function 18

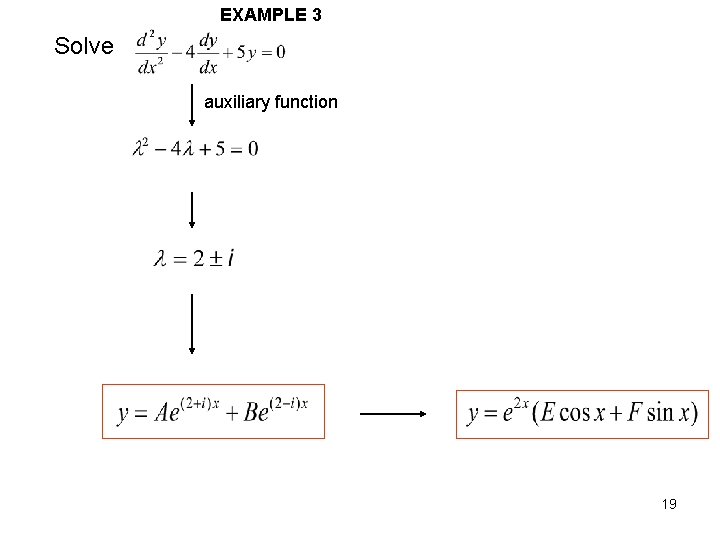
EXAMPLE 3 Solve auxiliary function 19

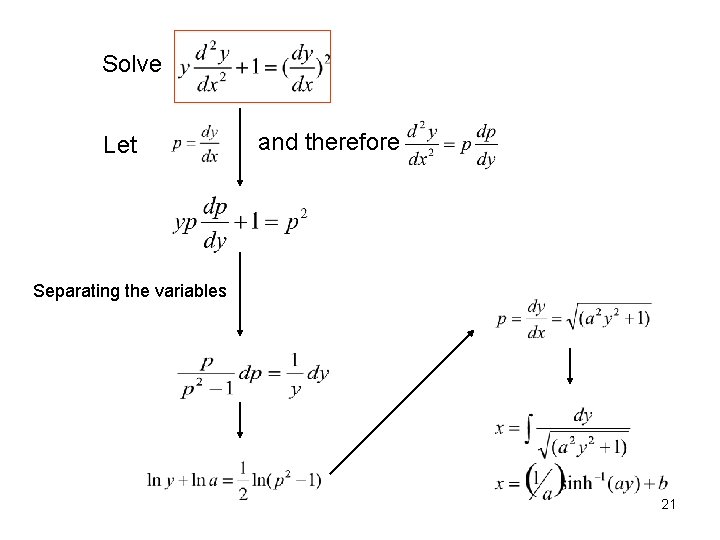
Non-linear 2 nd O. D. E. - Equations where the independent variables does not occur explicitly • They are solved by differentiation followed by the p substitution. • When the p substitution is made in this case, the second derivative of y is replaced as Let 20

Solve Let and therefore Separating the variables 21

2. 6. Nonhomogeneous Linear Equation ------(2. 9) The general solution: ◎ Two methods for finding (1) Variation of parameters -- Replace with homogeneous solution in the general Let Assume ------(2. 10) Compute 22
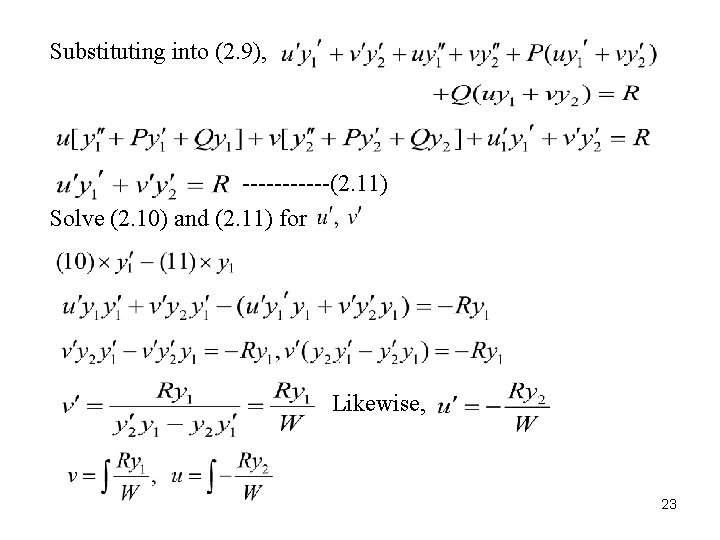
Substituting into (2. 9), ------(2. 11) Solve (2. 10) and (2. 11) for . Likewise, 23

。 Example 2. 15: ------(A) i) General homogeneous solution : Let. Substitute into (A) The characteristic equation: Complex solutions: Real solutions: : independent 24

ii) Nonhomogeneous solution Let 25
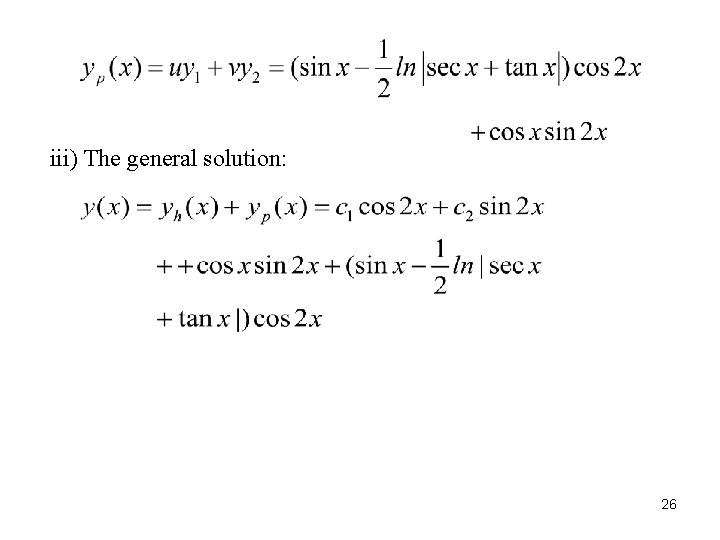
iii) The general solution: 26

(2) Undetermined coefficients Apply to A, B: constants Guess the form of e. g. from that of R : a polynomial Try a polynomial for : an exponential for Try an exponential for 27

。 Example 2. 19: ---(A) It’s derivatives can be multiples of or Try Compute Substituting into (A), 28

: linearly independent and The homogeneous solutions: The general solution: 29

。 Example 2. 20: ------(A) , try Substituting into (A), * This is because the guessed contains a homogeneous solution Strategy: If a homogeneous solution appears in any term of , multiply this term by x. If the modified term still occurs in a homogeneous solution, multiply by x again 30

Try Substituting into (A), 31

○ Steps of undetermined coefficients: (1) Find homogeneous solutions (2) From R(x), guess the form of If a homogeneous solution appears in any term of , multiply this term by x. If the modified term still occurs in a homogeneous solution, multiply by x again (3) Substitute the resultant into and solve for its coefficients 32

○ Guess Let from : a given polynomial , : polynomials with unknown coefficients Guessed 33

2. 6. 3. Superposition Let be a solution of is a solution of (A) 34

。 Example 2. 25: The general solution: where homogeneous solutions 35
 Integrating factor of differential equation
Integrating factor of differential equation Exponential differential equation
Exponential differential equation Parachute problem differential equations
Parachute problem differential equations Equations reducible to the linear form
Equations reducible to the linear form Euler algorithm
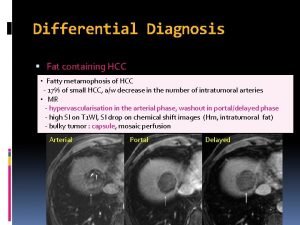
Euler algorithm Hcc differential equations
Hcc differential equations Definition of differential equation
Definition of differential equation How to solve linear ode
How to solve linear ode Hertz
Hertz Differential equations
Differential equations Kutta
Kutta Definition and classification of differential equations
Definition and classification of differential equations Piecewise differential equation
Piecewise differential equation Singular solution of ode
Singular solution of ode How to solve linear first order differential equations
How to solve linear first order differential equations Dennis g zill differential equations solutions
Dennis g zill differential equations solutions Homogeneous differential equation definition
Homogeneous differential equation definition Pde paula
Pde paula Separable partial differential equations
Separable partial differential equations Numerical methods for partial differential equations eth
Numerical methods for partial differential equations eth Derivation of maxwell's equations in differential form
Derivation of maxwell's equations in differential form Mixing problems differential equations
Mixing problems differential equations Cengage differential equations
Cengage differential equations Mechanical and electrical vibrations differential equations
Mechanical and electrical vibrations differential equations Differential equations with discontinuous forcing functions
Differential equations with discontinuous forcing functions Differential calculus
Differential calculus Traffic flow differential equations
Traffic flow differential equations Logistic growth curve equation
Logistic growth curve equation Integration of partial differential equation
Integration of partial differential equation Introduction to linear algebra strang
Introduction to linear algebra strang First order ode
First order ode Stewart differential equations
Stewart differential equations First order differential equation
First order differential equation Cengage differential equations
Cengage differential equations Second order differential equation
Second order differential equation Partial differential equations
Partial differential equations