Chapter 2 SecondOrder Circuits 1 SecondOrder Circuits Chapter

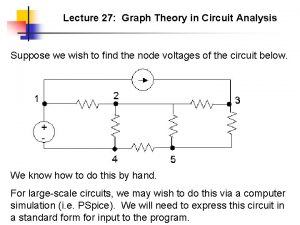
Chapter 2 Second-Order Circuits 1

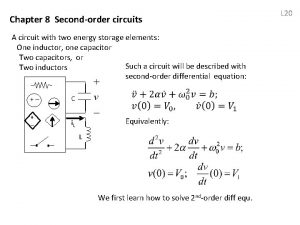
Second-Order Circuits Chapter 2 2. 1 2. 2 2. 3 2. 4 2. 5 Examples of 2 nd order RCL circuit The source-free series RLC circuit The source-free parallel RLC circuit Step response of a series RLC circuit Step response of a parallel RLC 2

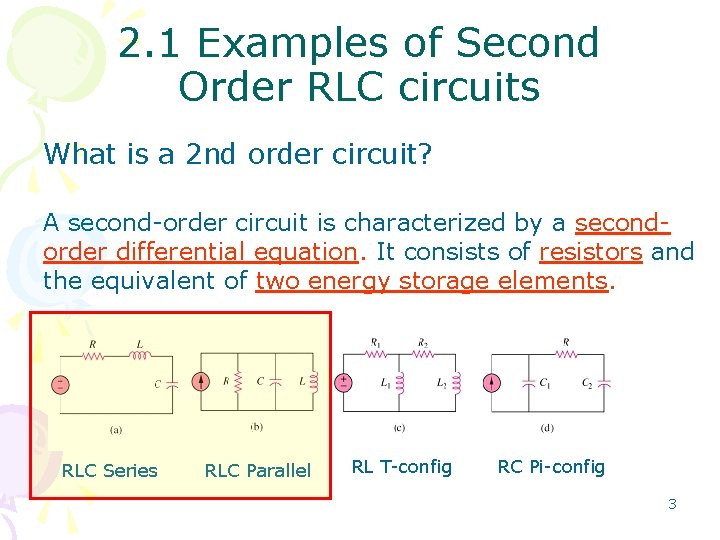
2. 1 Examples of Second Order RLC circuits What is a 2 nd order circuit? A second-order circuit is characterized by a secondorder differential equation. It consists of resistors and the equivalent of two energy storage elements. RLC Series RLC Parallel RL T-config RC Pi-config 3

2. 1 Second Order RLC circuits Analysis of second order circuits will be similar to that used for first order First consider circuits that are excited by the initial conditions of the storage elements Although these circuits may contain dependent sources, they are free of independent sources These source free circuits will give natural responses as expected 4

2. 1 Second Order RLC circuits Next will consider circuits that are excited by independent sources (dc) These circuits will give both the transient response and the steady-state response 5

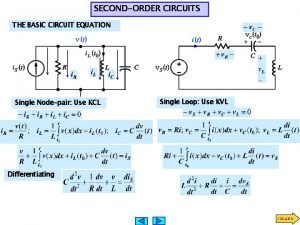
2. 1 Finding Initial and Final Values In handling second order circuit, it is essential to determine the initial and final conditions on circuit variables Next is to find the initial values of their derivatives Two key points in determining the initial conditions: -Carefully handle the polarity of voltage v(t) across the capacitor and the direction of the current i(t) through the inductor -Capacitor voltage is always continuous so that 6 v(0+) =v(0 -)

2. 1 Finding Initial and Final Values Inductor current is always continuous so that i(0+) =i(0 -) Where t = 0 - denotes the time just before a switching event and t = 0+ is the time just after the switching event, assuming that the switching event takes place at t = 0 7

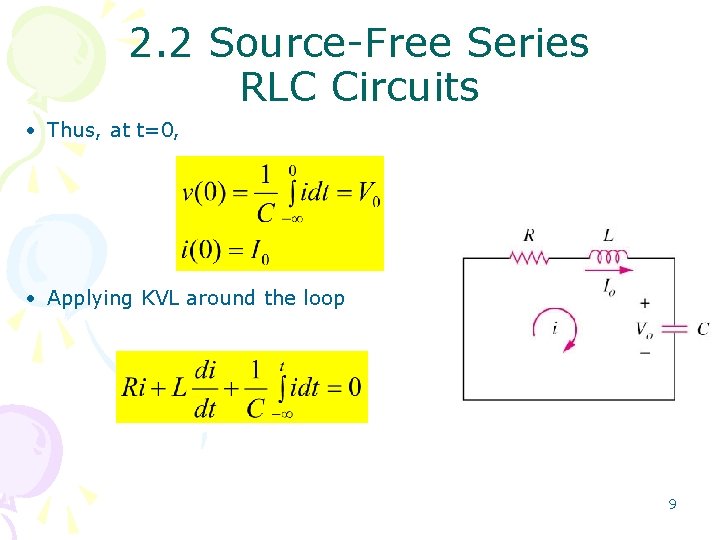
2. 2 Source-Free Series RLC Circuits • The solution of the source-free series RLC circuit is called as the natural response of the circuit. • The circuit is excited by the energy initially stored in the capacitor and inductor. • Consider the series RLC circuit • The circuit is being excited by the energy initially stored in the capacitor and inductor • The energy is represented by the initial capacitor voltage V 0 and initial inductor current I 0 8

2. 2 Source-Free Series RLC Circuits • Thus, at t=0, • Applying KVL around the loop 9

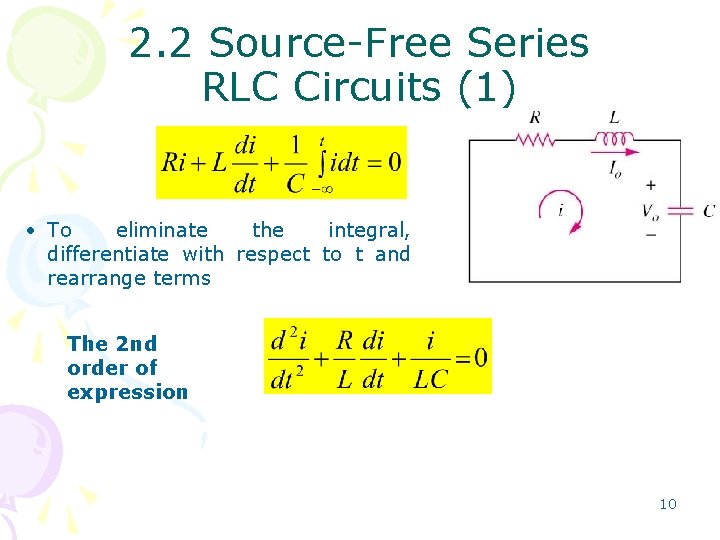
2. 2 Source-Free Series RLC Circuits (1) • To eliminate the integral, differentiate with respect to t and rearrange terms The 2 nd order of expression 10

2. 2 Source-Free Series RLC Circuits • To solve a second order differential equation requires two initial conditions, such as the initial value of i and its first derivative or initial values of some i and v • The initial value of i is • The initial value of the derivative of i is or 11

2. 2 Source-Free Series RLC Circuits • With the two initial conditions from and • We can solve • First order circuits suggests that the solution is of exponential form Let where A and s are constants to be determined 12

2. 2 Source-Free Series RLC Circuits • Substituting into and carrying out the differentiations, we get or 13

2. 2 Source-Free Series RLC Circuits Since is the assumed solution we are trying to find, only the expression in parentheses can be zero: This quadratic equation is known as the characteristic equation of the differential eq. since the roots dictate the character of i 14

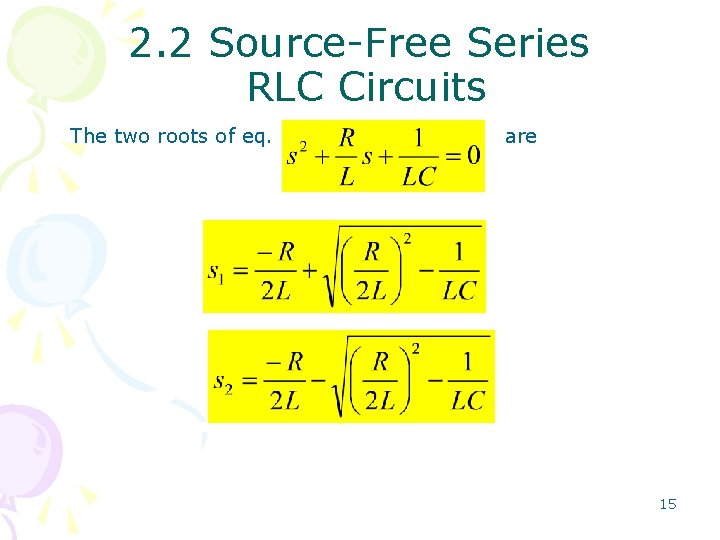
2. 2 Source-Free Series RLC Circuits The two roots of eq. are 15

2. 2 Source-Free Series RLC Circuits A more compact way of expressing the roots is where The roots s 1 and s 2 are called natural frequencies, measured in (Np/s), because they are associated with the natural response of the circuit; is known as the resonant frequency or undamped natural frequency, expressed in (rad/s) is the neper frequency or the damping factor, expressed in (Np/s) 16

2. 2 Source-Free Series RLC Circuits In terms of and , eq. can be written as The two values of s in eq. indicate that there are two possible solutions for i, that is, 17

2. 2 Source-Free Series RLC Circuits Since eq. is a linear equation, any linear combination of the two distinct solutions i 1 and i 2 is also a solution of eq. A complete solution of eq. is a linear combination of i 1 and i 2 18

2. 2 Source-Free Series RLC Circuits Thus, the natural response of the series RLC circuit is where the constants A 1 and A 2 are determined from the initial values i(0) and di(0)/dt in eqs. and 19

2. 2 Source-Free Series RLC Circuits From eq. , we can infer that there are three types of solutions: 1. If > o, over-damped case 2. If = o, critical damped case 3. If < o, under-damped case 20

2. 2 Source-Free Series RLC Circuits Overdamped Case ( > o) > o implies C > 4 L/R 2 When this happens, both roots s 1 and s 2 are negative and real The response is which decays and approaches zero as t increases 21

2. 2 Source-Free Series RLC Circuits Critically Damped Case ( = o) = o , C = 4 L/R 2 and Eq. yields where A 3 = A 1 + A 2. This cannot be the solution, because the two initial conditions cannot be satisfied with the single constant A 3 Referring to eq. when = o=R/2 L eq. 22

2. 2 Source-Free Series RLC Circuits or Let then eq. which is a first order differential eq. with solution where A 1 is a constant Eq. then becomes 23

2. 2 Source-Free Series RLC Circuits This can be written as Integrating both sides yields where A 2 is another constant. Hence, the natural response of the critically damped circuit is a sum of two terms: a negative exponential and a negative exponential multiplied by a linear term, or 24

2. 2 Source-Free Series RLC Circuits A typical critically damped response is shown below It is a sketch of i(t)=te- t , which reaches a maximum value at t= 1/ , one time constant, and then decays all the way to zero. 25

2. 2 Source-Free Series RLC Circuits Underdamped Case ( < o) For < o, C < 4 L/R 2. The roots may be written as where j= -1 and , which is called the damping frequency Both are natural frequencies because they help determine the natural response; while is often called the undamped natural frequency, is called the damped natural frequency 26

2. 2 Source-Free Series RLC Circuits The natural response is Using Euler’s identities, we get Replacing constants (A 1 + A 2) and j(A 1 - A 2) with constants B 1 and B 2, 27

2. 2 Source-Free Series RLC Circuits With the presence of sine and cosine functions, it is clear that the natural response for this case is exponentially damped and oscillatory in nature The response has a time constant of 1/ and a period of T=2 / d Once the inductor current i(t) is found for the RLC series circuit, other circuit quantities such as individual element voltages can easily be found 28

2. 2 Source-Free Series RLC Circuits Properties of an RLC network: 1. The behavior of such a network is captured by the idea of damping, which is the gradual loss of the initial stored energy(decrease in the amplitude) The damping effects due to the presence of resistance R The damping factor determines the rate at which the response is damped. If R = 0, then =0, and we have an LC circuit with 1/√LC as the undamped natural frequency Since < o in this case, the response is not only undamped but also oscillatory The circuit is said to be loss less, because the dissipating or damping element (R) is absent By adjusting the value of R, the response may be undamped, overdamped, critically damped, or underdamped 29

2. 2 Source-Free Series RLC Circuits 2. Oscillatory response is possible due to the presence of the two types of storage elements Having both L and C allows the flow of energy back and forth between the two The damped oscillation exhibited by the underdamped response is known as ringing 3. It is difficult to tell from the waveforms the difference between the overdamped and critically damped responses The critically damped case is the borderline between the underdamped and overdamped cases and it decays the fastest With the same initial conditions, the overdamped case has the longest settling time, because it takes the longest time to dissipate the initial stored energy If we desire the response that approaches the final value most rapidly without oscillation or ranging, the critically 30 damped circuit is the right choice

2. 2 Source-Free Series RLC Circuits Example 1 If R = 10 Ω, L = 5 H, and C = 2 m. F, find , ω0, s 1 and s 2. What type of natural response will the circuit have? • Please refer to lecture or textbook for more detail elaboration. Answer: 1, 10, -1 j 9. 95, underdamped 31

2. 2 Source-Free Series RLC Circuits Example 2 The circuit shown below has reached steady state at t = 0 -. If the make-before-break switch moves to position b at t = 0, calculate i(t) for t > 0. • Please refer to lecture or textbook for more detail elaboration. Answer: i(t) = e– 2. 5 t[5 cos 1. 6583 t – 7. 538 sin 1. 6583 t] A 32

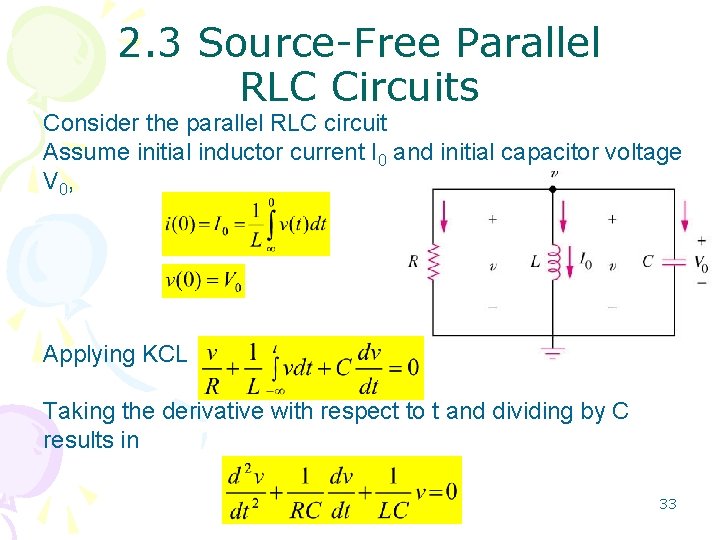
2. 3 Source-Free Parallel RLC Circuits Consider the parallel RLC circuit Assume initial inductor current I 0 and initial capacitor voltage V 0, Applying KCL Taking the derivative with respect to t and dividing by C results in 33

2. 3 Source-Free Parallel RLC Circuits We obtain the characteristic eq. by replacing the first derivative by s and the second derivative by s 2 The characteristic eq. is obtained as The roots of the eq. are or where 34

2. 3 Source-Free Parallel RLC Circuits There are three possible solutions, depending on whether > o , = o or < o Overdamped Case ( > o) > o when L > 4 R 2 C. The roots of the characteristics eq. are real and negative. The response is Critically Damped Case ( = o) = o , L = 4 R 2 C. The roots are real and equal so that the response is 35

2. 3 Source-Free Parallel RLC Circuits Underdamped Case ( < o) < o when L < 4 R 2 C. The roots are complex and may be expressed as Where The response is The constants A 1 and A 2 in each case can be determined from the initial conditions We need v(0) and dv(0)/dt 36

2. 3 Source-Free Parallel RLC Circuits Underdamped Case ( < o) The first term is known from v(0)=V 0 (initial capacitor voltage) We find the second term by combining initial inductor current and initial capacitor voltage with eq. as or The voltage waveforms will depend on whether the circuit is overdamped, underdamped, or critically damped 37

2. 3 Source-Free Parallel RLC Circuits Having found the capacitor voltage v(t), we can obtain other circuit quantities such as individual elements currents We first found the inductor current i(t) for the RLC series circuit, whereas we first found the capacitor voltage v(t) for the parallel RLC circuit 38

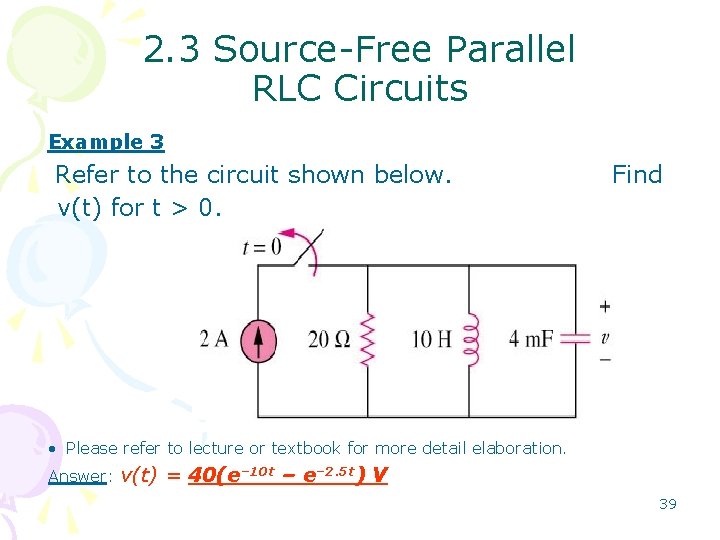
2. 3 Source-Free Parallel RLC Circuits Example 3 Refer to the circuit shown below. v(t) for t > 0. Find • Please refer to lecture or textbook for more detail elaboration. Answer: v(t) = 40(e– 10 t – e– 2. 5 t) V 39

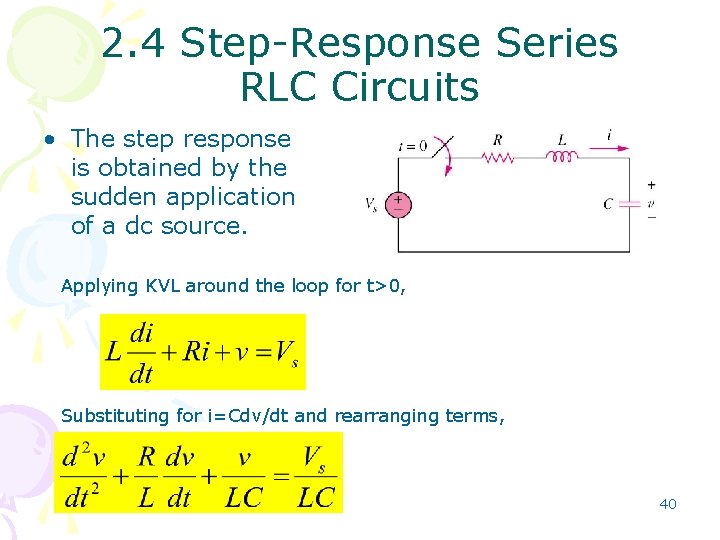
2. 4 Step-Response Series RLC Circuits • The step response is obtained by the sudden application of a dc source. Applying KVL around the loop for t>0, Substituting for i=Cdv/dt and rearranging terms, 40

2. 4 Step-Response Series RLC Circuits • The step response is obtained by the sudden application of a dc source. The 2 nd order of expression The above equation has the same form as the equation for source-free series RLC circuit. • The same coefficients (important in determining the frequency parameters). • Different circuit variable in the equation. 41

2. 4 Step-Response Series RLC Circuits (2) The solution of the equation should have two components: the transient response vt(t) & the steady-state response vss(t): The transient response vt is the same as that for source-free case (over-damped) (critically damped) (under-damped) The steady-state response is the final value of v(t). Ø vss(t) = v(∞) The values of A 1 and A 2 are obtained from the initial conditions: Ø v(0) and dv(0)/dt. 42

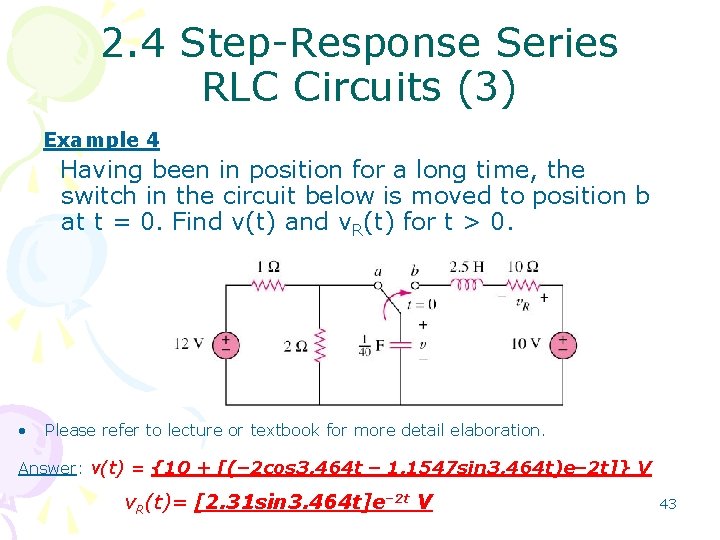
2. 4 Step-Response Series RLC Circuits (3) Example 4 Having been in position for a long time, the switch in the circuit below is moved to position b at t = 0. Find v(t) and v. R(t) for t > 0. • Please refer to lecture or textbook for more detail elaboration. Answer: v(t) = {10 + [(– 2 cos 3. 464 t – 1. 1547 sin 3. 464 t)e– 2 t]} V v. R(t)= [2. 31 sin 3. 464 t]e– 2 t V 43

2. 5 Step-Response Parallel RLC Circuits (1) • The step response obtained by the sudden application a dc source. is of The 2 nd order of expression It has the same form as the equation for source-free parallel RLC circuit. • The same coefficients (important in determining the frequency parameters). • Different circuit variable in the equation. 44

2. 5 Step-Response Parallel RLC Circuits (2) The solution of the equation should have two components: the transient response vt(t) & the steady-state response vss(t): The transient response it is the same as that for source-free case (over-damped) (critical damped) (under-damped) The steady-state response is the final value of i(t). Ø iss(t) = i(∞) = Is The values of A 1 and A 2 are obtained from the initial conditions: Ø i(0) and di(0)/dt. 45

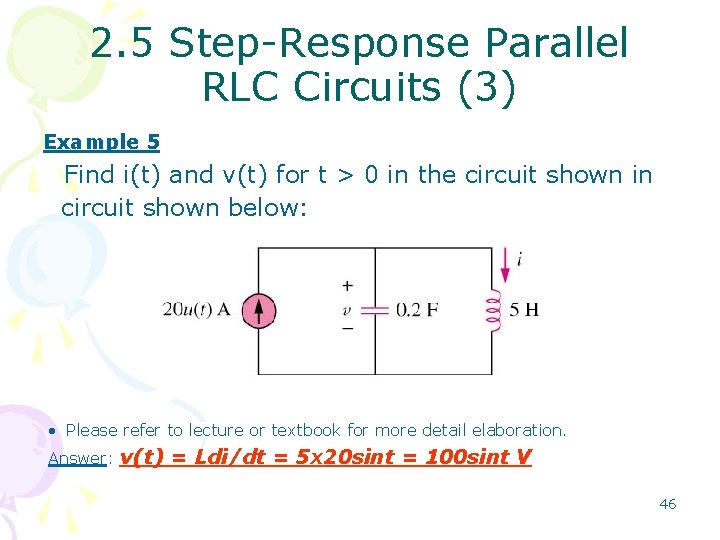
2. 5 Step-Response Parallel RLC Circuits (3) Example 5 Find i(t) and v(t) for t > 0 in the circuit shown in circuit shown below: • Please refer to lecture or textbook for more detail elaboration. Answer: v(t) = Ldi/dt = 5 x 20 sint = 100 sint V 46