Chapter 16 Curve Fitting Splines Spline Interpolation z

Chapter 16 Curve Fitting: Splines

Spline Interpolation z. There are cases where polynomial interpolation is bad z. Noisy data z. Sharp Corners (slope discontinuity) z. Humped or Flat data Ø Overshoot Ø Oscillations

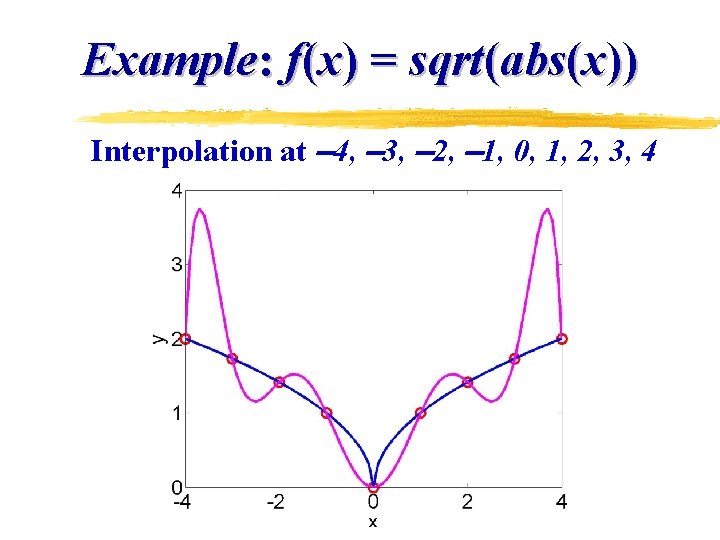
Example: f(x) = sqrt(abs(x)) Interpolation at 4, 3, 2, 1, 0, 1, 2, 3, 4

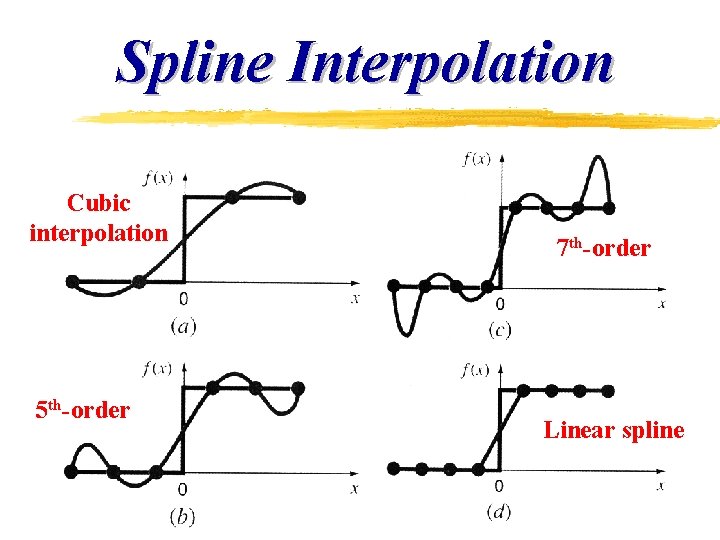
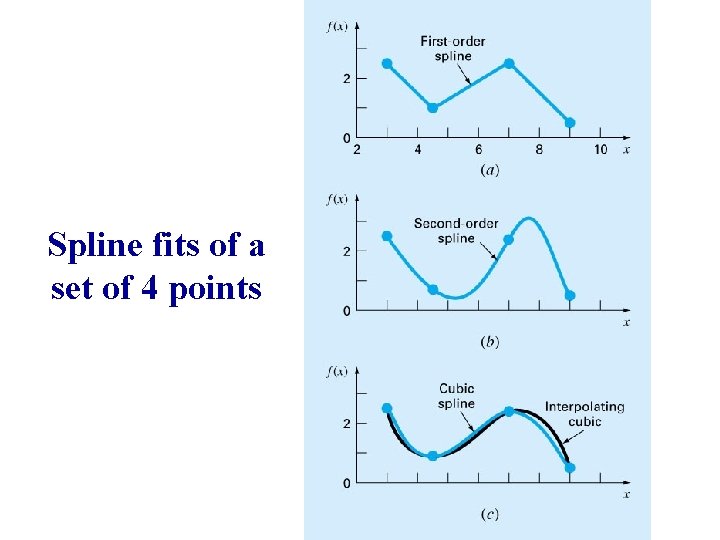
Spline Interpolation Cubic interpolation 5 th-order 7 th-order Linear spline

Spline Interpolation Idea behind splines • Use lower order polynomials to connect subsets of data points • Make connections between adjacent splines smooth • Lower order polynomials avoid oscillations and overshoots

Spline Interpolation z Use “piecewise” polynomials instead of a single polynomial z Spline -- a thin, flexible metal or wooden lath z Bent the lath around pegs at the required points z Spline curves -- curves of minimum strain energy z Piecewise Linear Interpolation z Piecewise Quadratic Interpolation z Piecewise Cubic Interpolation (cubic splines)

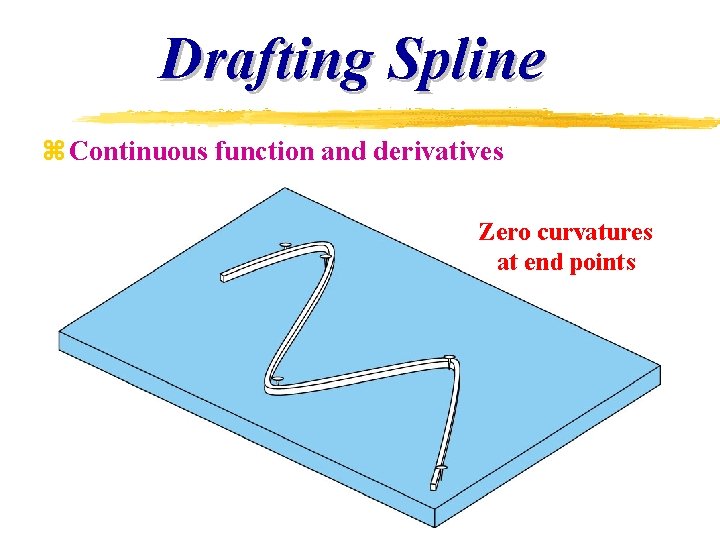
Drafting Spline z Continuous function and derivatives Zero curvatures at end points

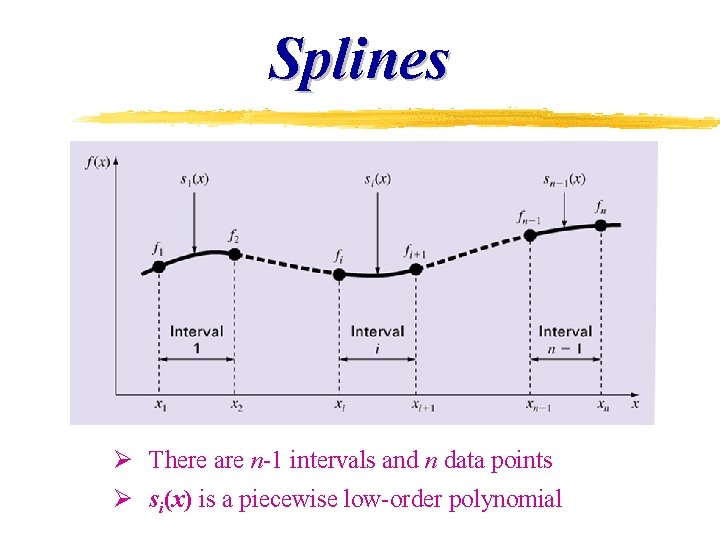
Splines Ø There are n-1 intervals and n data points Ø si(x) is a piecewise low-order polynomial

Spline fits of a set of 4 points

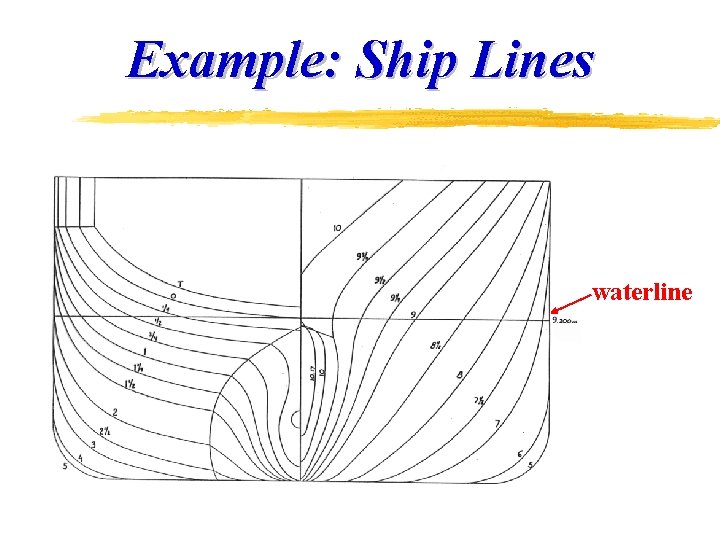
Example: Ship Lines waterline

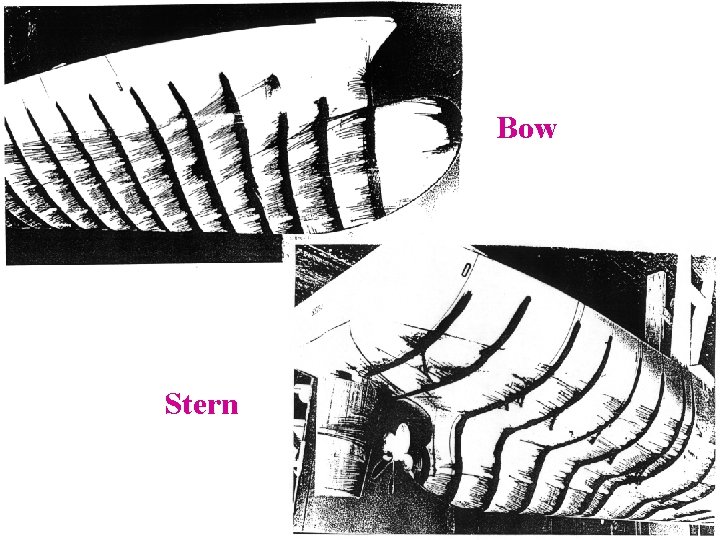
Bow Stern

Original database Spline interpolation for submerged hull (below waterline)

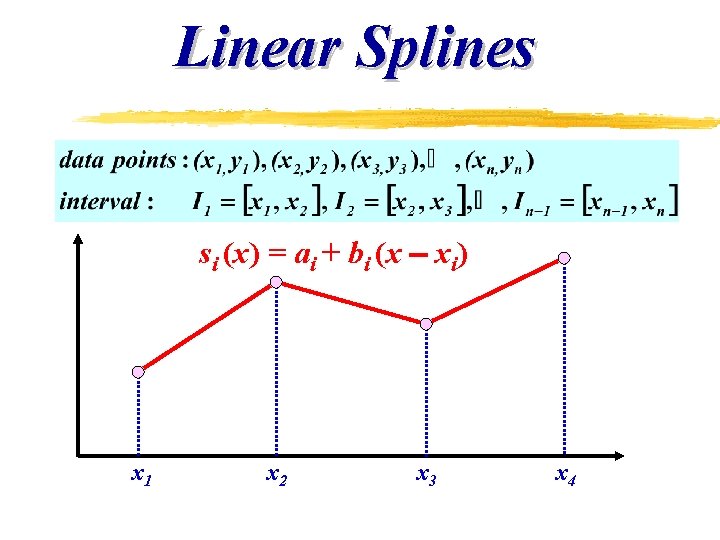
Linear Splines z Connect each two points with straight line functions connecting each pair of points b is the slope between points

Linear Splines si (x) = ai + bi (x xi) x 1 x 2 x 3 x 4

Linear Splines Identical to Lagrange interpolating polynomials

Linear splines Ø Connect each two points with straight line Ø Functions connecting each pair of points are Ø slope

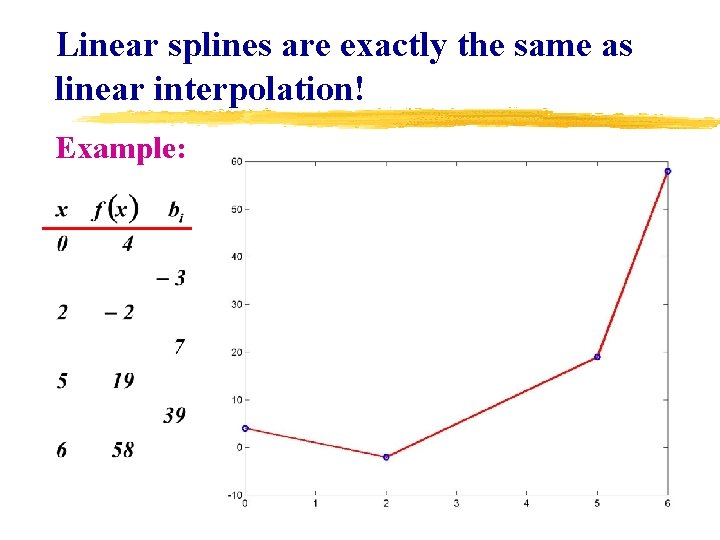
Linear splines are exactly the same as linear interpolation! Example:

Linear Splines z. Problem with linear splines -- not smooth at data points (or knots) z. First derivative (slope) is not continuous z. Use higher-order splines to get continuous derivatives z. Equate derivatives at neighboring splines z. Continuous functional values and derivatives

Quadratic Splines Quadratic splines - continuous first derivatives May have discontinuous second and higher derivatives Derive second order polynomial between each pair of points For n points (i=1, …, n): (n-1) intervals & 3(n-1) unknown parameters (a’s, b’s, and c’s) Need 3(n-1) equations

Quadratic Splines x) ( s 1 f(x 2) s 2 (x) f(x 3) s 3 (x) f(x 4) s 4 (x) f(x 5) f(x 1) Interval 1 x 2 Interval 3 x 3 si(x) = ai + bi (x xi) + ci(x xi)2 Interval 4 x 5 3(n-1) unknowns

Piecewise Quadratic Splines Example with n = 5 1. The functional must pass through all the points xi (continuity condition) 2. The function values of adjacent polynomials must be equal at all nodes (identical to condition 1. ) 2(n-2) + 2 = 2(n-1) 3. The 1 st derivatives are continuous at interior nodes xi, (n-2) 4. Assume that the second derivatives is zero at the first points 2(n 1) + (n 2) + (1) = 3(n 1) equations for 3(n 1) unknowns

Piecewise Quadratic Splines z Function must pass through all the points x = xi (2 n 2 eqns) z This also ensure the same function values of adjacent polynomials at the interior knots (hi = xi+1 – xi) z Apply to every interval (4 intervals, 8 equations)

Piecewise Quadratic Splines z Continuous slope at interior knots x = xi (n 2 equations) z Apply to interior knots x 2 , x 3 and x 4 (3 equations) z Zero curvatures at x = x 1 (1 equation)

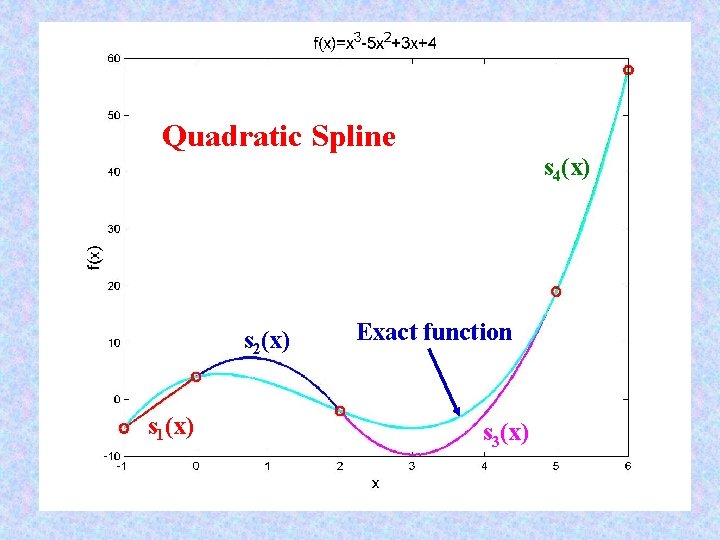
Example: Quadratic Spline

Quadratic Spline Interpolation function [A, b] = quadratic(x, f) % exact solution f(x)=x^3 -5 x^2+3 x+4 % x=[-1 0 2 5 6]; f=[-5 4 -2 19 58]; h 1=x(2)-x(1); h 2=x(3)-x(2); h 3=x(4)-x(3); h 4=x(5)-x(4); f 1=f(1); f 2=f(2); f 3=f(3); f 4=f(4); f 5=f(5); A=[1 0 0 0 h 1^2 0 0 0 1 0 0 0 h 2^2 0 0 0 1 0 0 0 h 3^2 0 0 0 1 0 0 0 h 4^2 0 1 2*h 1 0 -1 0 0 0 1 2*h 2 0 -1 0 0 0 1 2*h 3 0 -1 0 0 0 0]; b=[f 1; f 2 -f 1; f 2; f 3 -f 2; f 3; f 4 -f 3; f 4; f 5 -f 4; 0; 0];

Quadratic Spline Interpolation >> x=[-1 0 2 5 6]; f=[-5 4 -2 19 58]; >> [A, b]=quadratic(x, f) p = Ab -5. 0000 9. 0000 0 4. 0000 9. 0000 -6. 0000 -2. 0000 -15. 0000 7. 3333 19. 0000 29. 0000 10. 0000 dx = 0. 1; z 1=x(1): dx: x(2); s 1=p(1)+p(2)*(z 1 -x(1))+p(3)*(z 1 -x(1)). ^2; z 2=x(2): dx: x(3); s 2=p(4)+p(5)*(z 2 -x(2))+p(6)*(z 2 -x(2)). ^2; z 3=x(3): dx: x(4); s 3=p(7)+p(8)*(z 3 -x(3))+p(9)*(z 3 -x(3)). ^2; z 4=x(4): dx: x(5); s 4=p(10)+p(11)*(z 4 -x(4))+p(12)*(z 4 -x(4)). ^2; H=plot(z 1, s 1, 'r', z 2, s 2, 'b', z 3, s 3, 'm', z 4, s 4, 'g'); xx=-1: 0. 1: 6; fexact=xx. ^3 -5*xx. ^2+3*xx+4; hold on; G=plot(xx, fexact, 'c', x, f, 'ro'); set(H, 'Line. Width', 3); set(G, 'Line. Width', 3, 'Marker. Size', 8); H 1=xlabel('x'); set(H 1, 'Font. Size', 15); H 2=ylabel('f(x)'); set(H 2, 'Font. Size', 15); H 3=title('f(x)=x^3 -5 x^2+3 x+4'); set(H 3, 'Font. Size', 15);

Quadratic Spline s 2(x) s 1(x) s 4(x) Exact function s 3(x)

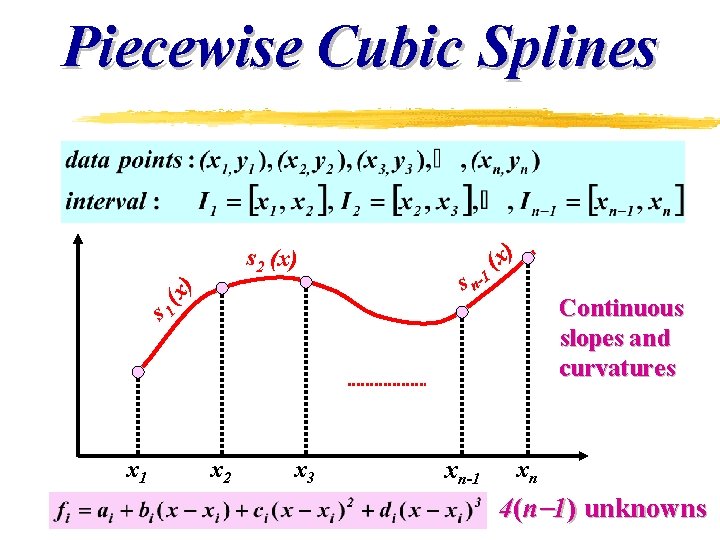
Cubic Splines Cubic splines avoid the straight line and the over-swing Can develop method like we did for quadratic – 4(n– 1) unknowns – 4(n– 1) equations Ø interior knot equality Ø end point fixed Ø interior knot first derivative equality Ø assume derivative value if needed

Piecewise Cubic Splines s n-1 (x) Continuous slopes and curvatures s 1 (x ) s 2 (x) x 1 x 2 x 3 xn-1 xn 4(n 1) unknowns

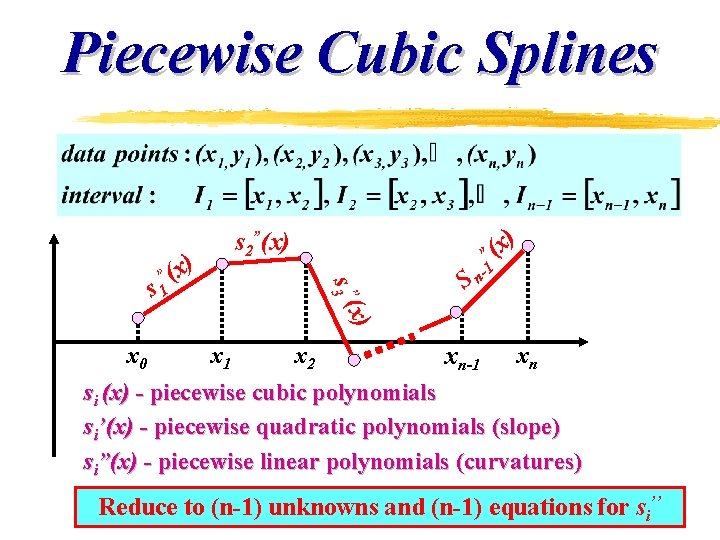
Piecewise Cubic Splines x 0 ) ” x) s 3 ( ” (x s 1 ) x ”( s 2”(x) x 1 x 2 S nxn-1 1 xn si (x) - piecewise cubic polynomials si’(x) - piecewise quadratic polynomials (slope) si”(x) - piecewise linear polynomials (curvatures) Reduce to (n-1) unknowns and (n-1) equations for si’’

Cubic Splines z Piecewise cubic polynomial with continuous derivatives up to order 2 1. The function must pass through all the data points gives 2(n-1) equations i = 1, 2, …, n-1

Cubic Splines 2. First derivatives at the interior nodes must be equal: (n-2) equations 3. Second derivatives at the interior nodes must be equal: (n-2) equations

Cubic Splines 4. Two additional conditions are needed (arbitrary) The last two equations Total equations: 2(n-1) + (n-2) +2 = 4(n-1)

Cubic Splines Ø Solve for (ai, bi, ci, di) – see textbook for details Ø Tridiagonal system with boundary conditions c 1 = cn= 0

Cubic Splines Tridiagonal matrix

Hand Calculations

Hand Calculations Ø can be further simplified since c 1 = c 4 = 0 (natural spline)

Cubic Spline Interpolation

Cubic Splines Ø Piecewise cubic splines (cubic polynomials)

Cubic Spline Interpolation z The exact solution is a cubic function z Why cubic spline interpolation does not give the exact solution for a cubic polynomial? z Because the conditions on the end knots are different! z In general, f (x 0) 0 and f (xn) 0 !!

Cubic Spline Interpolation

>> xx=[-1 0 2 5 6]; f = [-5 4 -2 19 58]; >> Cubic_spline(xx, f); Resulting piecewise function: (i = 1) s 1 = (-5. 000000)+(11. 081218)*(x-(-1. 000000)) s 2 = (0. 000000)*(x-(-1. 000000)). ^2+(-2. 081218)*(x-(-1. 000000)). ^3 Resulting piecewise function: s 1 = (i = 2) (4. 000000)+(4. 837563)*(x-(0. 000000)) s 2 = (-6. 243655)*(x-(0. 000000)). ^2+(1. 162437)*(x-(0. 000000)). ^3 Resulting piecewise function: s 1 = (i = 3) (-2. 000000)+(-6. 187817)*(x-(2. 000000)) s 2 = (0. 730964)*(x-(2. 000000)). ^2+(1. 221658)*(x-(2. 000000)). ^3 Resulting piecewise function: s 1 = (i = 4) (19. 000000)+(31. 182741)*(x-(5. 000000)) s 2 = (11. 725888)*(x-(5. 000000)). ^2+(-3. 908629)*(x-(5. 000000)). ^3

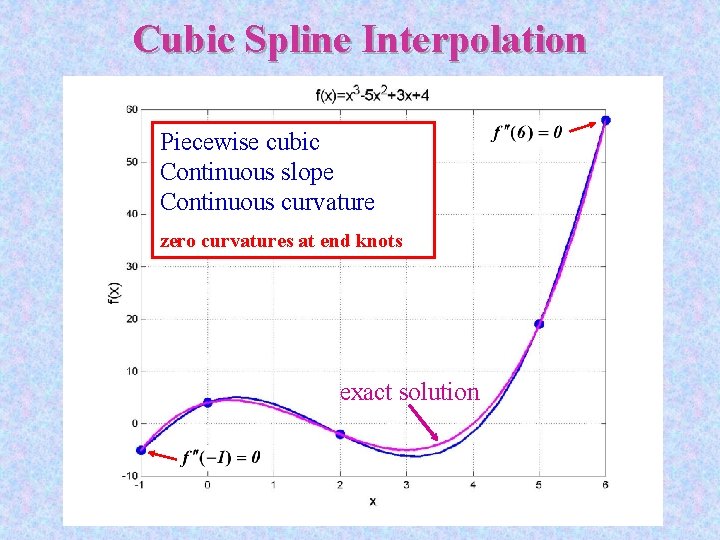
Cubic Spline Interpolation Piecewise cubic Continuous slope Continuous curvature zero curvatures at end knots exact solution

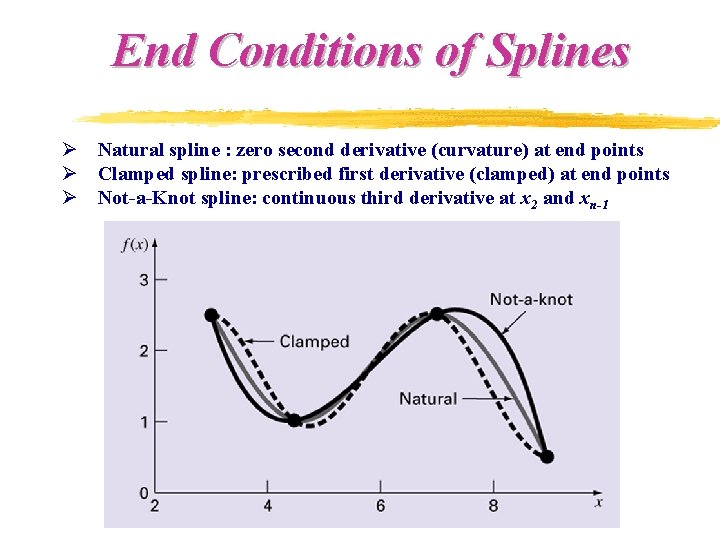
End Conditions of Splines Ø Natural spline : zero second derivative (curvature) at end points Ø Clamped spline: prescribed first derivative (clamped) at end points Ø Not-a-Knot spline: continuous third derivative at x 2 and xn-1

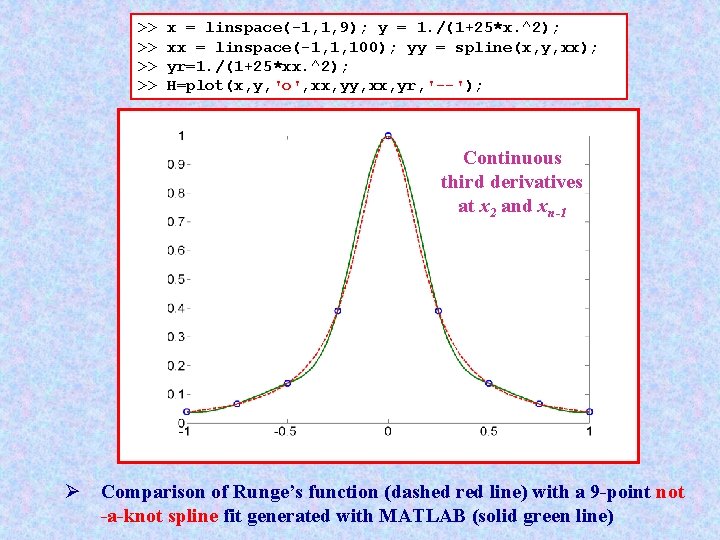
>> >> x = linspace(-1, 1, 9); y = 1. /(1+25*x. ^2); xx = linspace(-1, 1, 100); yy = spline(x, y, xx); yr=1. /(1+25*xx. ^2); H=plot(x, y, 'o', xx, yy, xx, yr, '--'); Continuous third derivatives at x 2 and xn-1 Ø Comparison of Runge’s function (dashed red line) with a 9 -point not -a-knot spline fit generated with MATLAB (solid green line)

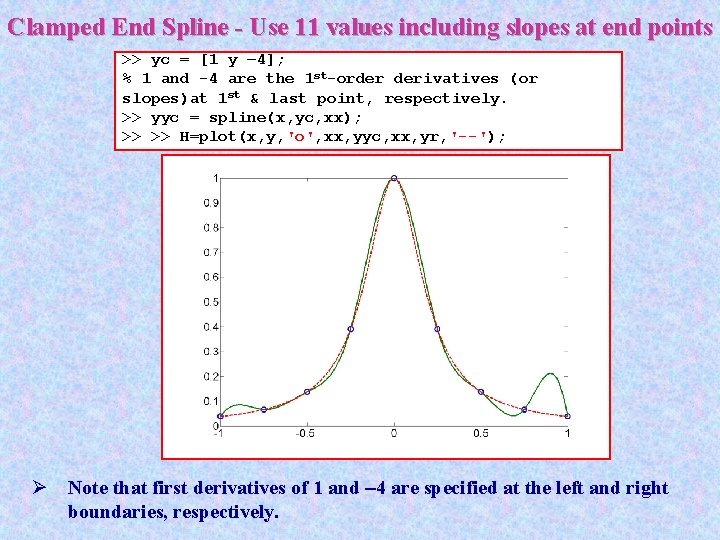
Clamped End Spline - Use 11 values including slopes at end points >> yc = [1 y – 4]; % 1 and -4 are the 1 st-order derivatives (or slopes)at 1 st & last point, respectively. >> yyc = spline(x, yc, xx); >> >> H=plot(x, y, 'o', xx, yyc, xx, yr, '--'); Ø Note that first derivatives of 1 and 4 are specified at the left and right boundaries, respectively.

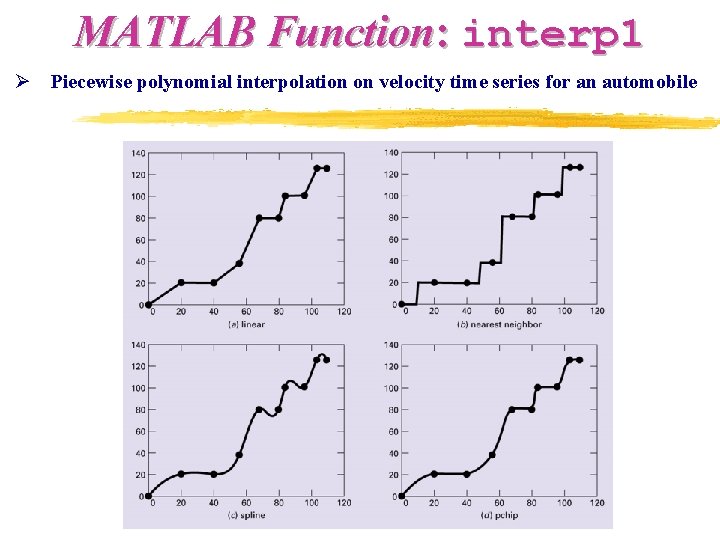
MATLAB Functions z One-dimensional interpolations z yy = spline (x, y, xx) z yi = interp 1 (x, y, xi, ‘method’) z yi = interp 1 (x, y, xi, ‘linear’) z yi = interp 1 (x, y, xi, ‘spline’) – not-a-knot spline z yi = interp 1 (x, y, , xi, ‘pchip’) – cubic Hermite z yi = interp 1 (x, y, , xi, ‘cubic’) – cubic Hermite z yi = interp 1 (x, y, , xi, ‘nearest’) – nearest neighbor

MATLAB Function: interp 1 Ø Piecewise polynomial interpolation on velocity time series for an automobile

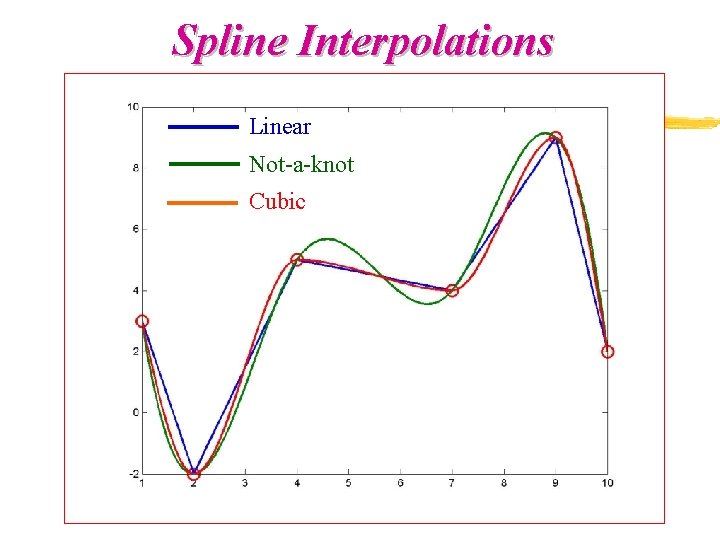
Spline Interpolations >> x=[1 2 4 7 9 10] x = 1 2 4 7 9 10 4 9 2 >> y=[3 -2 5 4 9 2] y = 3 -2 5 >> xi=1: 0. 1: 10; >> y 1=interp 1(x, y, xi, 'linear'); >> y 2=interp 1(x, y, xi, 'spline'); >> y 3=interp 1(x, y, xi, 'cubic'); >> plot(x, y, 'ro', xi, y 1, xi, y 2, xi, y 3, 'Line. Width', 2, 'Marker. Size', 12) >> print -djpeg spline 00. jpg

Spline Interpolations Linear Not-a-knot Cubic

MATLAB’s Functions z. Two-dimensional interpolations zzi = interp 2 (x, y, z, xi, yi)

MATLAB Function: interp 2 >> >> >> [x, y, z]=peaks(100); [xi, yi]=meshgrid(-3: 0. 1: 3, -3: 0. 1: 3); zi = interp 2(x, y, z, xi, yi); surf(xi, yi, zi) print -djpeg 075 peaks 1. jpg [x, y, z]=peaks(10); [xi, yi]=meshgrid(-3: 0. 1: 3, -3: 0. 1: 3); zi = interp 2(x, y, z, xi, yi); surf(xi, yi, zi) print -djpeg 075 peaks 2. jpg 100 data base 10 data base

CVEN 302 -501 Homework No. 11 z Chapter 16 z Problem 16. 1(a) (30) – Hand Calculation z Problem 16. 1(b) (20)– MATLAB program not-a-knot spline: yy = spline(x, y, xx) z Problem 16. 1(c)(20) – MATLAB program z Chapter 19 z Problem 19. 2 (20)– Hand Calculation z Problem 19. 4 (20)– Hand Calculation z Due on Wed. 11/05/08 at the beginning of the period