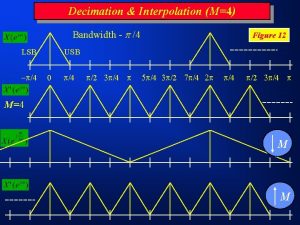
Interpolation Decimation Sampling period T at the output

Interpolation & Decimation • Sampling period T , at the output INPUT 1 OUTPUT • Interpolation by m: • Let the OUTPUT be [i. e. Samples exist at all instants n. T] • then INPUT is [i. e. Samples exist at instants m. T] Professor A G Constantinides

Interpolation & Decimation • Let Digital Filter transfer function be then • Hence is of the form i. e. its impulse response exists at the instants m. T. • Write 2 Professor A G Constantinides

Interpolation & Decimation • Or • Where • So that 3 Professor A G Constantinides

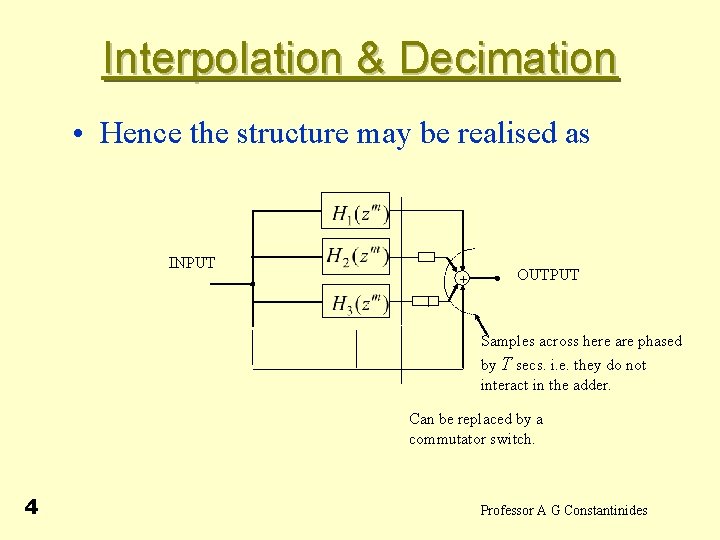
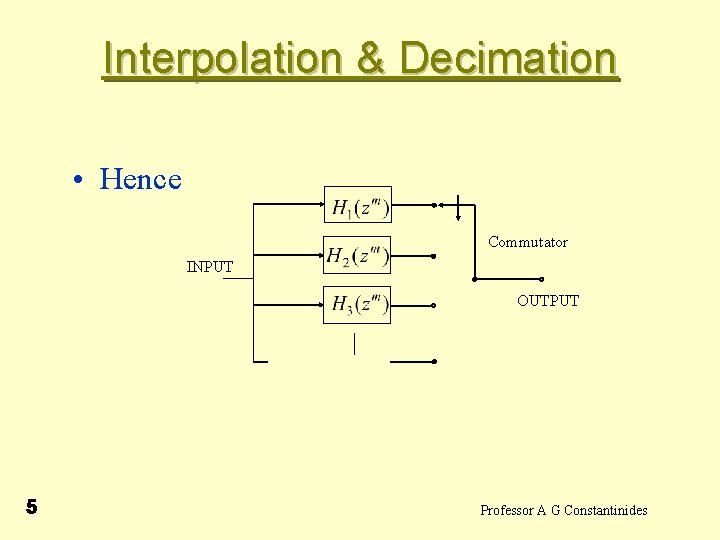
Interpolation & Decimation • Hence the structure may be realised as INPUT + OUTPUT Samples across here are phased by T secs. i. e. they do not interact in the adder. Can be replaced by a commutator switch. 4 Professor A G Constantinides

Interpolation & Decimation • Hence Commutator INPUT OUTPUT 5 Professor A G Constantinides

Interpolation & Decimation • Decimation by m: • Let Input be (i. e. Samples exist at all instants n. T) • Let Output be (i. e. Samples exist at instants m. T) • With digital filter transfer function we have 6 Professor A G Constantinides

Interpolation & Decimation • Set • And • Where in both expressions the subsequences are constructed as earlier. Then 7 Professor A G Constantinides

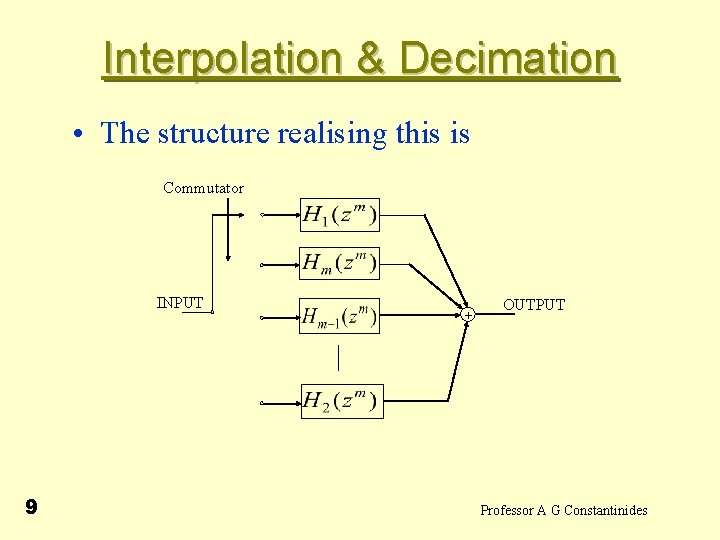
Interpolation & Decimation • Any products that have powers of less than m do not contribute to , as this is required to be a function of . • Therefore we retain the products 8 Professor A G Constantinides

Interpolation & Decimation • The structure realising this is Commutator INPUT 9 + OUTPUT Professor A G Constantinides

Interpolation & Decimation • For FIR filters why Downsample and then Upsample? LOW PASS LENGTH N #MULT/ACC DOWNSAMPLE M: 1 LOW PASS UPSAMPLE 1: M LOW PASS LENGTH N #MULT/ACC TOTAL #MULT/ACC 10 Professor A G Constantinides

Interpolation & Decimation • A very useful FIR transfer function special case is for : N odd, symmetric • with additional constraints on to be zero at the points shown in the figure. 11 Professor A G Constantinides

Interpolation & Decimation • For the impulse response shown • The amplitude response is then given • In general 12 Professor A G Constantinides

Interpolation & Decimation • Now consider • Then 13 Professor A G Constantinides

Interpolation & Decimation • Hence • Also • Or • For a normalised response 14 Professor A G Constantinides

Interpolation & Decimation • Thus • The shifted response is useful 15 Professor A G Constantinides

Design of Decimator and Interpolator • Example Develop the specs suitable for the design of a decimator to reduce the sampling rate of a signal from 12 k. Hz to 400 Hz • The desired down-sampling factor is therefore M = 30 as shown below 16 Professor A G Constantinides

Multistage Design of Decimator and Interpolator • Specifications for the decimation filter H(z) are assumed to be as follows: , 17 Professor A G Constantinides

Polyphase Decomposition The Decomposition • Consider an arbitrary sequence {x[n]} with a z-transform X(z) given by • We can rewrite X(z) as where 18 Professor A G Constantinides

Polyphase Decomposition • The subsequences are called the polyphase components of the parent sequence {x[n]} • The functions , given by the z -transforms of , are called the polyphase components of X(z) 19 Professor A G Constantinides

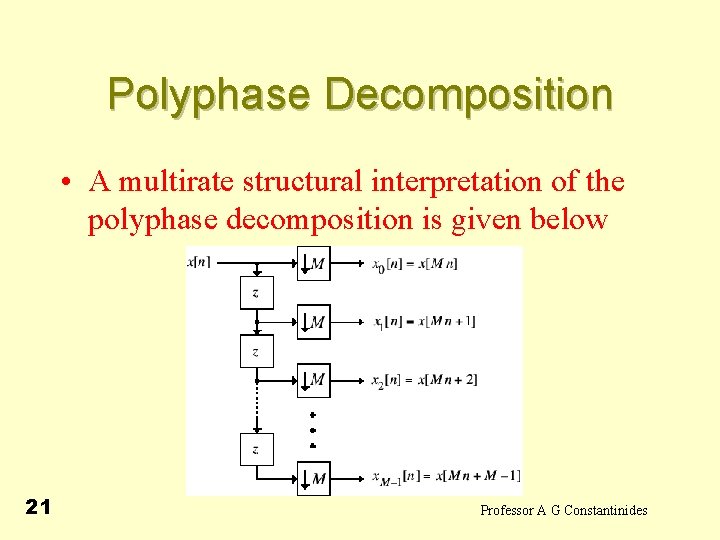
Polyphase Decomposition • The relation between the subsequences and the original sequence {x[n]} are given by • In matrix form we can write 20 Professor A G Constantinides

Polyphase Decomposition • A multirate structural interpretation of the polyphase decomposition is given below 21 Professor A G Constantinides

Polyphase Decomposition • The polyphase decomposition of an FIR transfer function can be carried out by inspection • For example, consider a length-9 FIR transfer function: 22 Professor A G Constantinides

Polyphase Decomposition • Its 4 -branch polyphase decomposition is given by where 23 Professor A G Constantinides

Polyphase Decomposition • The polyphase decomposition of an IIR transfer function H(z) = P(z)/D(z) is not that straight forward • One way to arrive at an M-branch polyphase decomposition of H(z) is to express it in the form by multiplying P(z) and D(z) with an appropriately chosen polynomial and then apply an M-branch polyphase decomposition to 24 Professor A G Constantinides

Polyphase Decomposition • Example - Consider • To obtain a 2 -band polyphase decomposition we rewrite H(z) as • Therefore, where 25 Professor A G Constantinides

Polyphase Decomposition • The above approach increases the overall order and complexity of H(z) • However, when used in certain multirate structures, the approach may result in a more computationally efficient structure • An alternative more attractive approach is discussed in the following example 26 Professor A G Constantinides

Polyphase Decomposition • Example - Consider the transfer function of a 5 -th order Butterworth lowpass filter with a 3 -d. B cutoff frequency at 0. 5 p: • It is easy to show that H(z) can be expressed as 27 Professor A G Constantinides

Polyphase Decomposition • Therefore H(z) can be expressed as where 28 Professor A G Constantinides

Polyphase Decomposition • In the above polyphase decomposition, branch transfer functions are stable allpass functions (proposed by Constantinides) • Moreover, the decomposition has not increased the order of the overall transfer function H(z) 29 Professor A G Constantinides

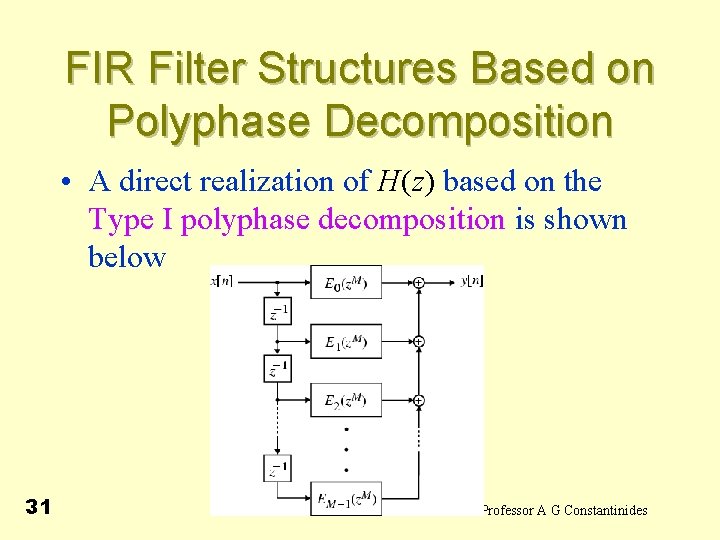
FIR Filter Structures Based on Polyphase Decomposition • We shall demonstrate later that a parallel realization of an FIR transfer function H(z) based on the polyphase decomposition can often result in computationally efficient multirate structures • Consider the M-branch Type I polyphase decomposition of H(z): 30 Professor A G Constantinides

FIR Filter Structures Based on Polyphase Decomposition • A direct realization of H(z) based on the Type I polyphase decomposition is shown below 31 Professor A G Constantinides

FIR Filter Structures Based on Polyphase Decomposition • The transpose of the Type I polyphase FIR filter structure is indicated below 32 Professor A G Constantinides