STAT 1060 Week 6 SAMPLING TECHNIQUES Course Overview

STAT 1060 Week 6 SAMPLING TECHNIQUES

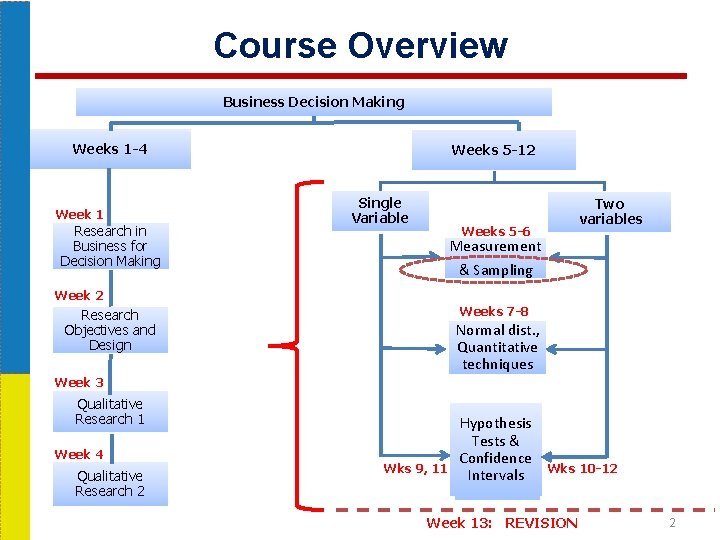
Course Overview Business Decision Making Weeks 1 -4 Week 1 Research in Business for Decision Making Weeks 5 -12 Single Variable Weeks 5 -6 Two variables Measurement & Sampling Week 2 Research Objectives and Design Weeks 7 -8 Normal dist. , Quantitative techniques Week 3 Qualitative Research 1 Week 4 Qualitative Research 2 Hypothesis Tests & Confidence Wks 9, 11 Confidence Wks 10 -12 Intervals Week 13: REVISION 2

REVISION QUESTION 1 A consumer confidence researcher asks several retailers to report the number of LCD televisions sold during a particular month. These numbers most likely represent what variable type? A) NOMINAL B) ORDINAL C) DISCRETE D) CONTINUOUS

REVISION QUESTION 2 A company publishes data on its quarterly earnings for its stockholders to evaluate. What is the variable type? A) NOMINAL B) ORDINAL C) DISCRETE D) CONTINUOUS

REVISION QUESTION 3 Which of the following can be described as a nominal variable? A) Annual income B) Age C) Annual sales D) Geographical location of a firm

Aims of Week 6 1. What is Sampling 1 -6 2. When to use a Larger Sample 3. What is a Valid Sample - Accurate - Precise 4. Types of Sampling Designs

1. What is Sampling? • Sampling: by selecting some of the elements in a population, we may draw conclusions about the entire population. • I. e. , the idea of sampling is to study a part (the sample) in order to gain information about the whole (the population). Sample Population 1 -7

Simple Example of Sampling • In this photo, a young girl is sampling a watermelon. • How many bites would she need to take to determine if it was to her liking? 1 -8

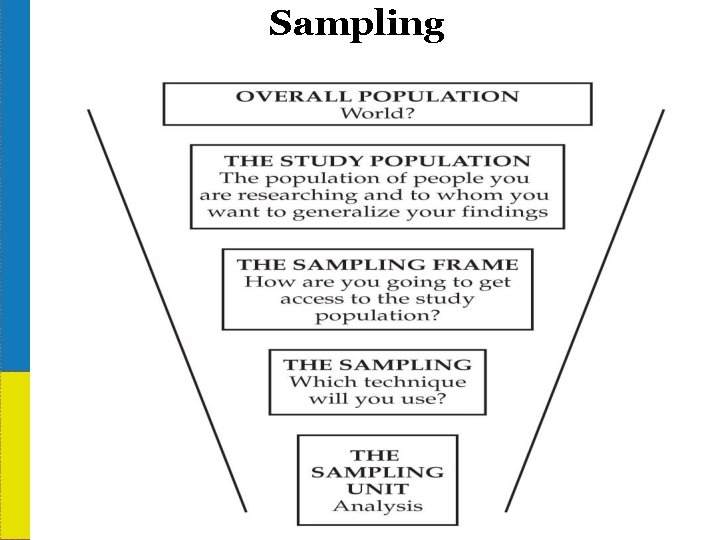
Sampling –Terminology • A population element is the individual participant or object on which the measurement is taken. It is the unit of study. It may be a person but it could also be any object. • E. g. , Individual Household Accounting record, Advertisement, Slab of beer • A population is the total collection of elements about which we wish to make an inference • A census is a count of all the elements in a population. • A sampling frame is a list of all the population elements from which the sample is drawn from the population. E. g. , all numbers in a telephone book, electoral register • Sample: A subset, or some part, of a larger population Ideally you want the sample to be representative of the population 1 -9

Sampling Frame - Example Recap: List of elements in population from which the sample is drawn • Stay at home dads might be a difficult sampling frame to come by. • Where might you gather data to build the sampling frame from? 1 -10

Sampling nit

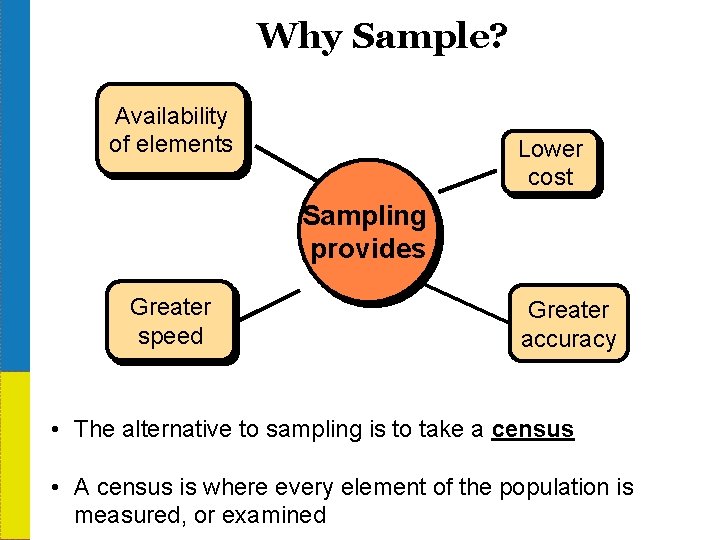
Why Sample? Availability of elements Lower cost Sampling provides Greater speed Greater accuracy • The alternative to sampling is to take a census • A census is where every element of the population is measured, or examined 1 -12

QUESTION 1 • Hilton Hotels wishes to conduct a study on the determinants of brand loyalty among Hilton Hotel customers. • The Hilton organization estimates that 10% of its 2, 600, 000 Hilton Honors club members are loyal to the Hilton brand wherever they travel. • However, the remaining members may choose other hotel brands at times. The organization wants to understand how to increase loyalty among the other 90% of club members. • The Hilton organization is considering a survey about factors affecting brand loyalty that will be sent to all of its Hilton Honors club members. This is an example of a: A. sampling element B. sample C. sampling frame D. census 1 -13

Why Sample - Example? • Why might there be problems with testing average battery life by taking a census? • To determine average battery life by a census, all batteries produced would need to be used until failure, thus would be no batteries left to 1 -14 sell to customers – not realistic! • A parameter is a numerical characteristic of the population E. g. : Population Mean • The mean is another word for average, and indicates the location of the data. • We take a sample and calculate the Mean of the sample. • This will give us some information about the population parameter. • The mean of the sample is an example of a statistic. • Statistics are a numerical summary of the sample, while a parameter is a numerical characteristic of the populationn. 1 -14

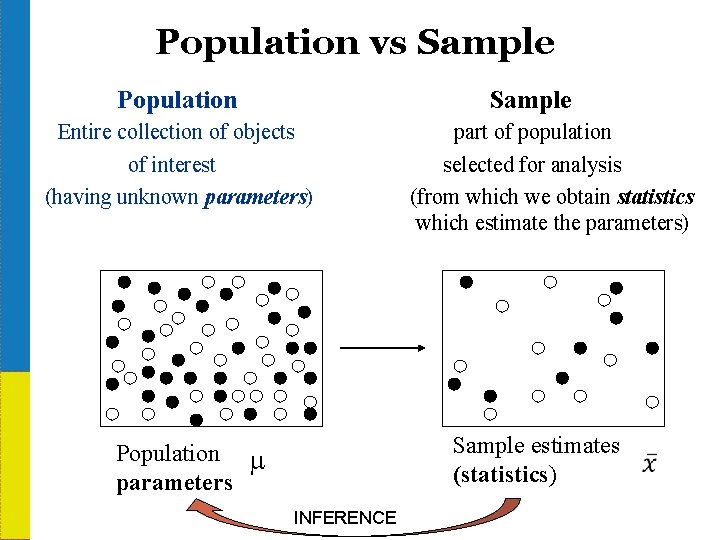
Population vs Sample Population Sample Entire collection of objects of interest (having unknown parameters) part of population selected for analysis (from which we obtain statistics which estimate the parameters) Sample estimates (statistics) Population m parameters INFERENCE

2. When to Use Larger Sample? • The greater the variation (variance) within the population, the larger the sample must be to provide estimation precision Population variance • The greater the desired precision of the estimate, Desired the larger the sample must be precision • The smaller the error range, the larger the sample must be Small error range • The higher the confidence level of estimate, the Confidence large the sample must be level • The greater the number of subgroups within a Number of sample, the greater the sample size must be, as each subgroups subgroup must meet minimum sample size requirements 1 -16

When is a Census Appropriate? Feasible Necessary • The advantages of sampling over census studies are less compelling when the population is small and the variability within population is high. • A census is feasible when the population is small and necessary when the elements are quite different from each other. • RARELY in practice would you obtain a census so most of the time you will have to rely on a SAMPLE. • SO HOW DO WE DETERMINE IF THE SAMPLE IS OKAY? 1 -17

3. What Is a Valid Sample? Accurate Precise Here a sample is being taken of water, using a can suspended on a fishing line. • The ultimate test of a sample design is how well it represents the characteristics of the population it is supposed to represent. • In measurement terms, the sample must be valid. • Validity of a sample depends on: • Accuracy and • Precision 1 -18

What Is a Valid Sample -> a. Accuracy “Accuracy is the degree to which bias is absent from the sample” • When the sample is drawn properly, the measure of behavior, attitudes, or knowledge of some sample elements will be less than the measure of those same variables drawn from the population; while measure of other sample elements will be more than the population values. • Variations in these sample values offset each other, resulting in a sample value that is close to the population value. • For these offsetting effects to occur, there must be enough elements in the sample and they must be drawn in a way that favors neither over- nor under-estimation. 1 -19

What Is a Valid Sample ->b. Precision • As well as accuracy, the precision of an estimate is the second criterion of a good sample design • The statistics that describe samples may be expected to differ from those that describe populations because of random fluctuations in the sampling process • This is called sampling error and reflects the influence of chance in drawing the sample members • Sampling error is what is left after all known sources of errors have been accounted for. • Precision is measured by the standard error of estimate (i. e. the variation or spread of the estimate) • The smaller the standard error, the higher the precision of the sample 1 -20

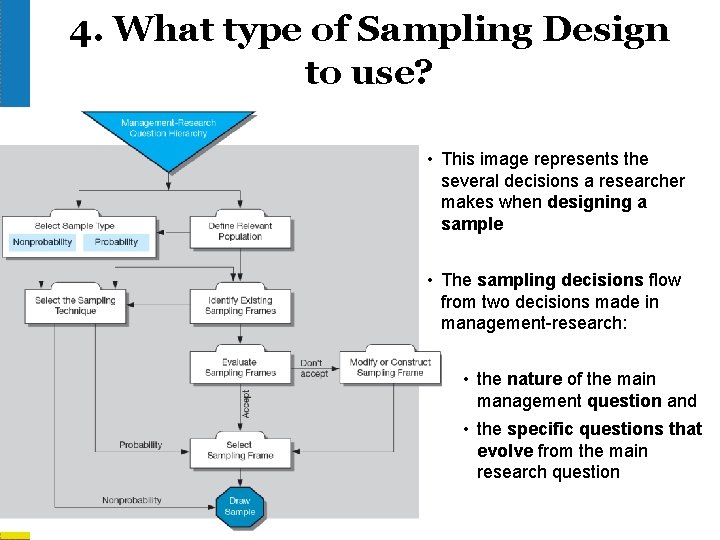
4. What type of Sampling Design to use? • This image represents the several decisions a researcher makes when designing a sample • The sampling decisions flow from two decisions made in management-research: • the nature of the main management question and • the specific questions that evolve from the main research question 1 -21

Types of Sampling Designs a. Probability b. Non-probability i. Simple random i. Convenience Complex random: Purposive: ii. Systematic ii. Judgment iii. Stratified iii. Quota iv. Cluster iv. Snowball v. Double 1 -22

Probability vs Non-probability Sampling 23 Probability Sampling § Sampling units are selected by chance § Can determine the precision of sample estimates § Can make inferences about the population from the sample Focus of the remainder of this course Non-probability Sampling ¢ May yield good estimates of population characteristics ¢ May be quicker, cheaper and easier to do ¢ Estimates are not statistically projectable to the population 1 -23

a. Probability Sampling • Each member of the population has a known chance of being selected • Some randomisation process is used • Requires a sampling frame Examples Simple Random Sampling Systematic (every nth member) Stratified (mutually exclusive groups, e. g. occupation, age) Cluster Double • Use when external validity (generalisability) is important • Probability sampling yields results close to that of the population! Statistical methods are based on probability sampling. Emphasis of STAT 1060 is on these methods 1 -24

i. Simple Random sample • Each population member (element) has an equal chance of being selected • The sample is drawn using a random number table or generator or by drawing names out of a hat • The probability of selecting each element is equal to the sample size divided by the population size. • What is the probability of selecting each of 10 products from a production line? 1 -25

Simple Random sample (ctd) Advantages Easy to implement with random dialing Disadvantages Requires list of population elements Time consuming and High cost Larger sample needed Produces larger errors 1 -26

ii. Systematic Sampling Systematically selecting the sample from the list of population members, such as: auditing records, production line or shoppers Example Sampling units chosen If you want a systematic sample of 20 slabs of beer from 141 slabs N = 141/20 = 7 (every 7 th slab) 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119, 126, 133, 140 Systematic = selecting every nth member i. e. An element of the population is selected at the beginning with a random start - Then every kth element is selected until the appropriate size is selected. - The kth element is the skip interval, the interval between sample elements drawn - It is determined by dividing the population size by the sample size. 1 -27

Systematic (ctd) To protect against subtle biases, the research can: - Randomize the population before sampling, - Change the random start several times in the process, and - Replicate a selection of different samples. Advantages Simple to design Easier than simple random Easy to determine sampling distribution of mean or proportion Disadvantages Periodicity within population may skew sample and results Trends in list may bias results Moderate cost 1 -28

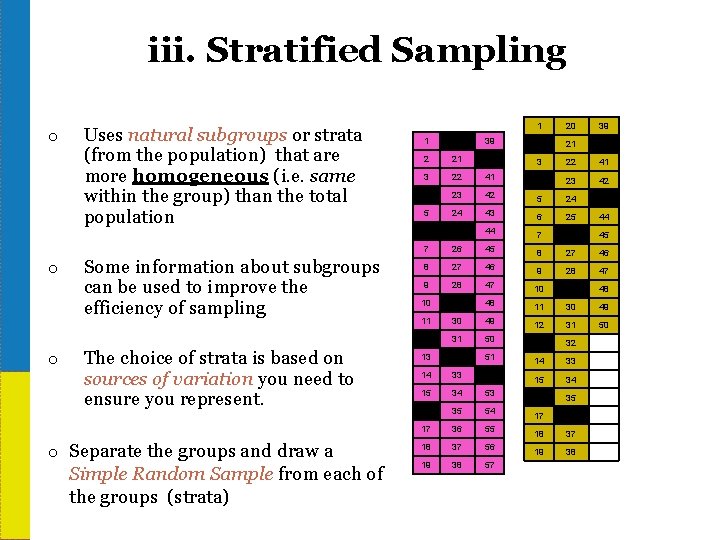
iii. Stratified Sampling o o o Uses natural subgroups or strata (from the population) that are more homogeneous (i. e. same within the group) than the total population Some information about subgroups can be used to improve the efficiency of sampling The choice of strata is based on sources of variation you need to ensure you represent. o Separate the groups and draw a Simple Random Sample from each of the groups (strata) 1 20 39 2 21 40 3 22 41 4 23 42 5 24 43 6 25 44 7 26 45 8 27 46 9 28 47 10 29 48 11 30 49 12 31 50 13 32 51 14 33 52 15 34 53 16 35 54 17 36 55 18 37 56 19 38 57 1 -29

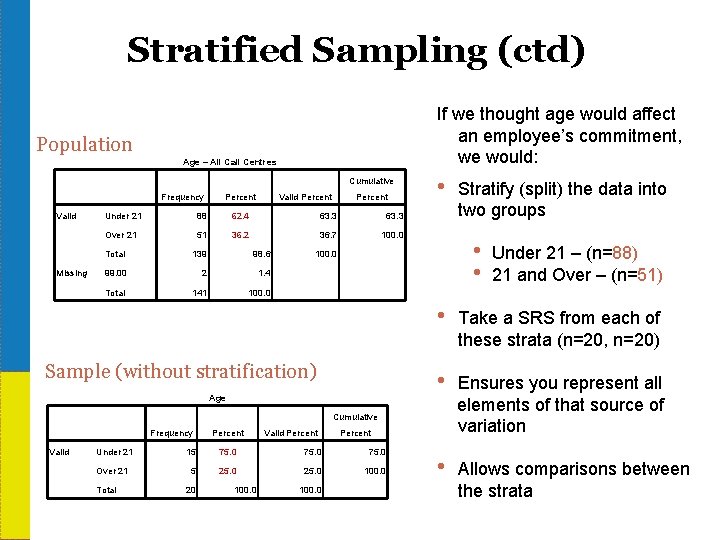
Stratified Sampling (ctd) If we thought age would affect an employee’s commitment, we would: Population Age – All Call Centres Cumulative Frequency Valid Missing Percent Valid Percent Under 21 88 62. 4 63. 3 Over 21 51 36. 2 36. 7 100. 0 Total 139 98. 6 99. 00 2 1. 4 Total 141 100. 0 • • Under 21 – (n=88) • 21 and Over – (n=51) 100. 0 • Sample (without stratification) Cumulative Valid Percent Under 21 15 75. 0 Over 21 5 25. 0 100. 0 Total 20 100. 0 Take a SRS from each of these strata (n=20, n=20) • Age Frequency Stratify (split) the data into two groups Ensures you represent all elements of that source of variation • Allows comparisons between the strata 1 -30

Stratified Sampling (ctd) • Stratified sampling may be proportionate or disproportionate. • In proportionate stratified sampling, each stratum’s size is proportionate to the stratum’s share of the population. • Any stratification that departs from the proportionate relationship is disproportionate. Advantages Control of sample size in strata Increased statistical efficiency Provides data to represent and analyze subgroups Enables use of different methods in strata Disadvantages Increased error if subgroups are selected at different rates Especially expensive if strata on population must be created High cost 1 -31

iv. Cluster Sampling § Similar to stratified sampling § Involves dividing population into subgroups (i. e. clusters) § Involves random sampling of the clusters and all members of the subgroup are sampled § Useful when the population is divided into mutually exclusive subgroups (or clusters), e. g. § § Suburbs Schools Slabs of beers on a production line Planes arriving at Newcastle Airport 1 -32

Cluster Sampling (ctd) • Population divided into heterogeneous subgroups. • Some are randomly selected for further study. • Use when there is a need for more economic efficiency than can be provided by simple random sampling; and • Unavailability of a practical sampling frame for individual elements. • Several questions must be answered when designing cluster samples. • • • How homogeneous are the resulting clusters? Shall we seek equal-sized or unequal-sized clusters? How large a cluster shall we take? Shall we use a single-stage or multistage cluster? How large a sample is needed? Advantages Provides an unbiased estimate of population parameters if properly done Economically more efficient than simple random Lowest cost per sample Easy to do without list Disadvantages Often lower statistical efficiency due to subgroups being homogeneous rather than heterogeneous Moderate cost 1 -33

QUESTION 2 Which of the following techniques yields a simple random sample of companies? A) Randomly selecting a district and then sampling all companies within the district B) Numbering all the elements of a company sampling frame and then using a random number table to pick companies from the table C) Listing companies by sector and choosing a proportion from within each sector at random D) Choosing volunteer companies to participate 1 -34

Clusters can be ‘Areas’ – ‘Area Sampling’ Well defined political or geographical boundaries Low cost Frequently used 1 -35

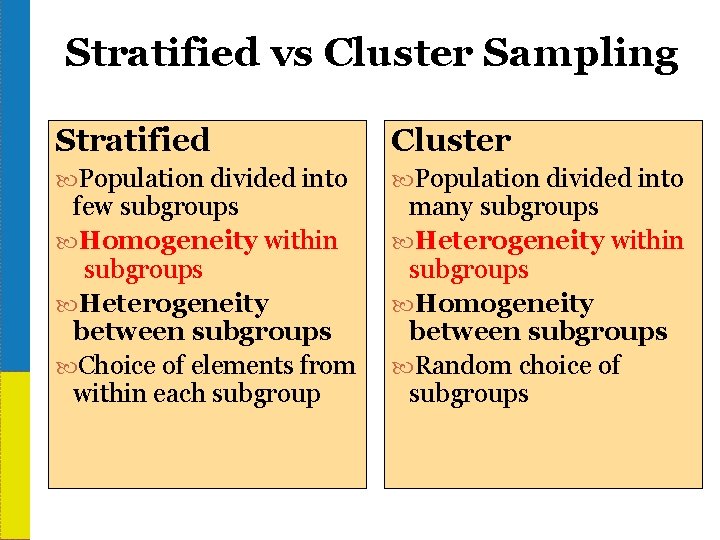
Stratified vs Cluster Sampling Stratified Cluster Population divided into few subgroups many subgroups Homogeneity within Heterogeneity within subgroups Heterogeneity Homogeneity between subgroups Choice of elements from Random choice of within each subgroups 1 -36

Summary of Probability sampling methods 37 1 -37

v. Double Sampling • In drawing a sample with double (sequential or multiphase) sampling, data are collected using a previously defined technique. • Based on the information found, a subsample is selected for further study. Advantages Disadvantages May reduce costs if first Increased costs if stage results in enough data to stratify or cluster the population indiscriminately used 1 -38

b. Nonprobability Samples • Subjective approach: Probability of selecting population elements is unknown. • Greater opportunity for bias in the sample and distorted findings. • However there are practical reasons to use nonprobability samples. ¢May yield good estimates of population characteristics ¢May be quicker, cheaper and easier to do ¢Estimates are not statistically projectable to the population Feasibility Time No need to generalize Limited objectives Cost 1 -39

Nonprobability Sampling Methods i. Convenience ii. Judgment iii. Quota iv. Snowball 1 -40

Non-probability Sampling Methods (ctd) i. Convenience samples • are non-probability samples where the element selection is based on ease of accessibility. • They are the least reliable but cheapest and easiest to conduct. • Examples include informal pools of friends and neighbours, people responding to an advertised invitation, and “on the street” interviews. 1 -41

Nonprobability Sampling Methods (ctd) PURPOSIVE Sampling can be: ii. Judgement Sampling: researcher arbitrarily selects sample units to conform to some criterion. • Appropriate for the early stages of an exploratory study. iii. Quota sampling Relevant characteristics are used to stratify the sample which should improve its representativeness. • Certain relevant characteristics describe dimensions of population. • In most quota samples, researchers specify more than one control dimension. Each dimension should have a distribution in the population that can be estimated and pertinent to topic studied. 1 -42

Nonprobability Sampling Methods (ctd) iv. Snowball sampling: • means that subsequent participants are referred by the current sample elements. • This is useful when respondents are difficult to identify and best located through referral networks. • It is also used frequently in qualitative studies. 1 -43

Revise: Selecting a sampling method Advantages Least expensive and time consuming Disadvantages Selection bias May not be representative of population Cannot generalise to the population Non-probability Sampling units are accessible, easy to measure Sampling and co-operative Random aspect may be able to be used Easily understood Results may be projected to target population Probability Sampling Different techniques (e. g. stratified) can help improve SRS results Stats tools applicable May be time-consuming, difficult and costly to do May be difficult to construct sample frame that will permit a SRS can result in large samples SRS may not result in as precise or representative sample may need to use a more complex technique (e. g. stratified, cluster, two 44 stage) SRS = simple random sampling 1 -44

QUESTION 3 When people are readily available, volunteer, or are easily recruited to the sample, this is called: A) Snowball sampling B) Convenience sampling C) Stratified sampling D) Random sampling 1 -45

QUESTION 4 Which ONE of these sampling methods is a probability method of sampling? A) Quota B) Judgement C) Convenience D) Simple random 1 -46

QUESTION 5 When each member of a population has an equal chance of being selected, this is called: A) A snowball sample B) A stratified sample C) A random sample D) A non-random sample 1 -47

Why were polls so wrong in 2016? (Trump vs Clinton) http: //www. pewresearch. org/fact-tank/2016/11/09/why-2016 -electionpolls-missed-their-mark/ 1. One likely culprit is what pollsters refer to as nonresponse bias. This occurs when certain kinds of people systematically do not respond to surveys despite equal opportunity outreach to all parts of the electorate. We know that some groups – including the less educated voters who were a key demographic for Trump on Election Day – are consistently hard for pollsters to reach. It is possible that the frustration and anti-institutional feelings that drove the Trump campaign may also have aligned with an unwillingness to respond to polls. The result would be a strongly pro. Trump segment of the population that simply did not show up in the polls in proportion to their actual share of the population. 48 1 -48

Why were polls so wrong in 2016? (Trump vs Clinton) 2. Some have also suggested that many of those who were polled simply were not honest about whom they intended to vote for. The idea of so-called “shy Trumpers” suggests that support for Trump was socially undesirable, and that his supporters were unwilling to admit their support to pollsters. This hypothesis is reminiscent of the supposed “Bradley effect, ” when Democrat Tom Bradley, the black mayor of Los Angeles, lost the 1982 California gubernatorial election to Republican George Deukmejian despite having been ahead in the polls, supposedly because voters were reluctant to tell interviewers that they were not going to vote for a black candidate. 49 1 -49

Why were polls so wrong in 2016? (Trump vs Clinton) The “shy Trumper” hypothesis has received a fair amount of attention this year. If this were the case, we would expect to see Trump perform systematically better in online surveys, as research has found that people are less likely to report socially undesirable behavior when they are talking to a live interviewer. Politico and Morning Consult conducted an experiment to see if this was the case, and found that overall, there was little indication of an effect, though they did find some suggestion that collegeeducated and higher-income voters might have been more likely to support Trump online. (*) In phone interviews, likely voters with a college degree said they support Clinton by a 21 -point margin, 60 percent to 39 percent. But online, that margin shrunk (sic) to just 7 points, 53 percent to 46 percent. Similarly, among likely voters in households earning more than $50, 000 annually, Clinton leads by 10 points over the phone, 54 percent to 44 percent. The candidates run neck-and-neck among these voters online, however: 50 percent for Trump, and 50 49 percent for Clinton. 1 -50

Why were polls so wrong in 2016? (Trump vs Clinton) 3. A third possibility involves the way pollsters identify likely voters. Because we can’t know in advance who is actually going to vote, pollsters develop models predicting who is going to vote and what the electorate will look like on Election Day. This is a notoriously difficult task, and small differences in assumptions can produce sizable differences in election predictions. We may find that the voters that pollsters were expecting, particularly in the Midwestern and Rust Belt states that so defied expectations, were not the ones that showed up. Because many traditional likely-voter models incorporate measures of enthusiasm into their calculus, 2016’s distinctly unenthused electorate – at least on the Democratic side – may have also wreaked some havoc with this aspect of measurement. 51 1 -51

Revision - Key Terms to be aware of Area sampling Multiphase sampling Census Nonprobability sampling Convenience sampling Population element Disproportionate stratified sampling Population parameters Double sampling Probability sampling Judgment sampling Cluster sampling 1 -52

Revision - Key Terms to be aware of (ctd) Proportionate Simple random stratified sampling Quota sampling Sample statistics Sampling error Sampling frame Sequential sampling sample Skip interval Snowball sampling Stratified random sampling Systematic sampling 1 -53