Sampling 1 Sampling Issues Sampling Terminology Probability in

Sampling 1

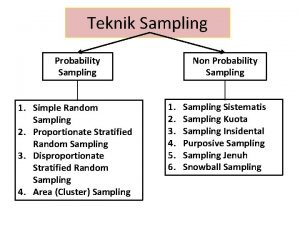
Sampling Issues Sampling Terminology Probability in Sampling Probability Sampling Designs Non-Probability Sampling Designs Sampling Distribution 2

Sampling Terminology 3

Two Major Types of Sampling Methods Probability Sampling uses some form of random selection requires that each unit have a known (often equal) probability of being selected Non-Probability Sampling selection is systematic or haphazard, but not random 4

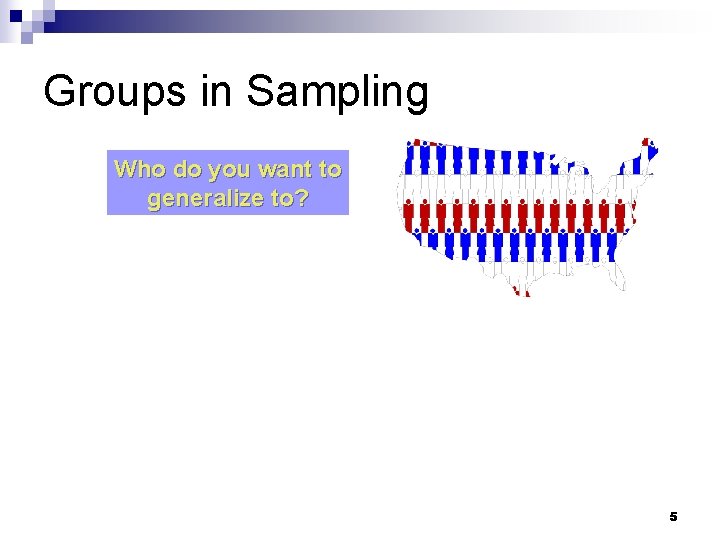
Groups in Sampling Who do you want to generalize to? 5

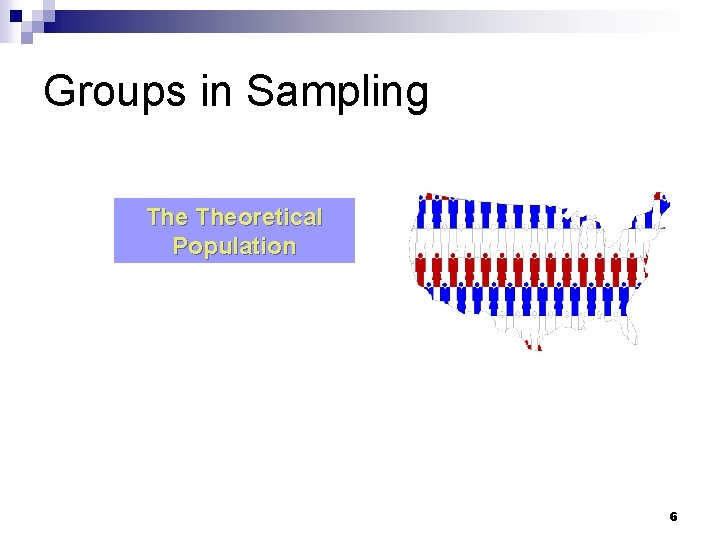
Groups in Sampling Theoretical Population 6

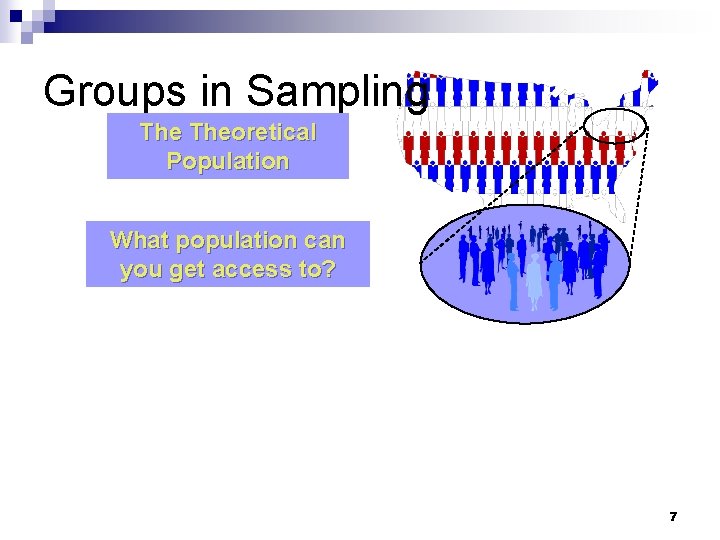
Groups in Sampling Theoretical Population What population can you get access to? 7

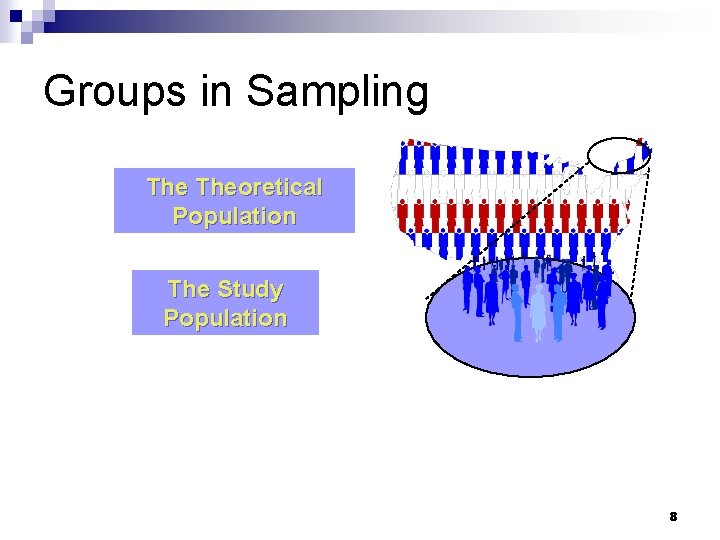
Groups in Sampling Theoretical Population The Study Population 8

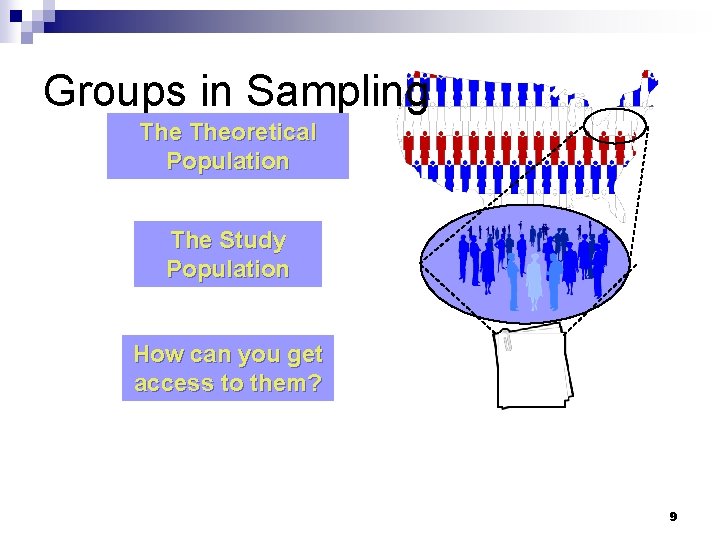
Groups in Sampling Theoretical Population The Study Population How can you get access to them? 9

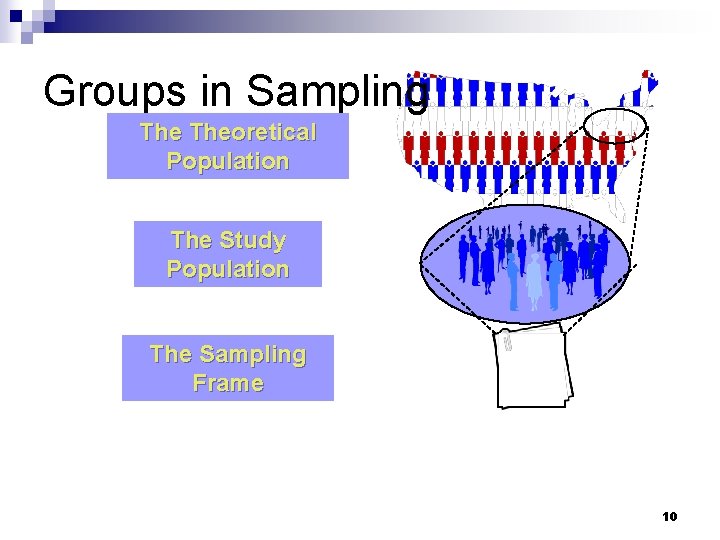
Groups in Sampling Theoretical Population The Study Population The Sampling Frame 10

Groups in Sampling Theoretical Population The Study Population The Sampling Frame Who is in your study? 11

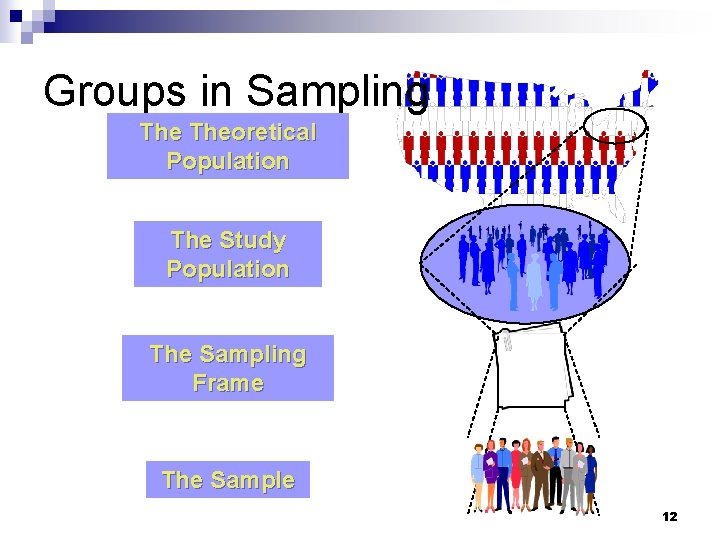
Groups in Sampling Theoretical Population The Study Population The Sampling Frame The Sample 12

Where Can We Go Wrong? Theoretical Population The Study Population The Sampling Frame The Sample 13

Where Can We Go Wrong? Theoretical Population The Study Population The Sampling Frame The Sample 14

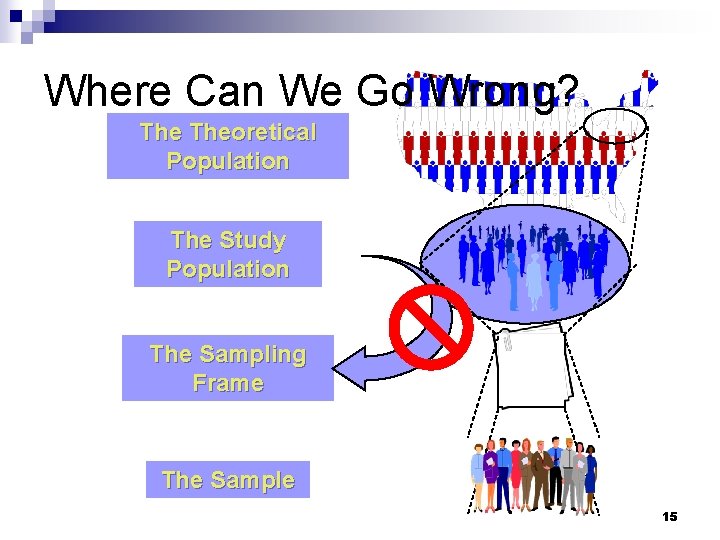
Where Can We Go Wrong? Theoretical Population The Study Population The Sampling Frame The Sample 15

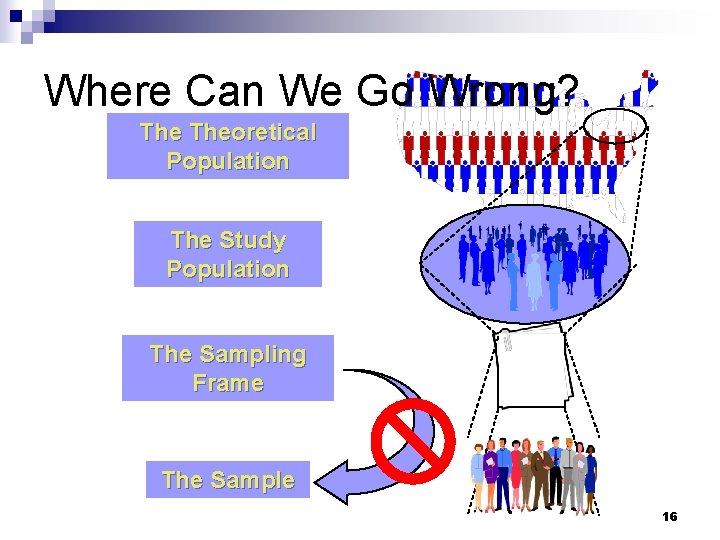
Where Can We Go Wrong? Theoretical Population The Study Population The Sampling Frame The Sample 16

Statistical Terms in Sampling Variable 17

Statistical Terms in Sampling Variable 1 2 3 4 5 responsibility 18

Statistical Terms in Sampling Variable 1 2 3 4 5 responsibility Statistic 19

Statistical Terms in Sampling Variable 1 2 3 4 5 responsibility Statistic Average = 3. 72 sample 20

Statistical Terms in Sampling Variable 1 2 3 4 5 responsibility Statistic Average = 3. 72 sample Parameter 21

Statistical Terms in Sampling Variable 1 2 3 4 5 response Statistic Average = 3. 72 sample Parameter Average = 3. 75 population 22

Statistical Inference n n n Statistical inference: make generalizations about a population from a sample. A population is the set of all the elements of interest in a study. A sample is a subset elements in the Thisofclass would not be a population chosengood to represent sample of it. all Persian Dentists, we are Quality of the sample = quality of more the interested in research inference methodology, so we are Would this class be a good representation of different!! all Persian Doctors? Why or why not? 23

The Sampling Distribution sample 24

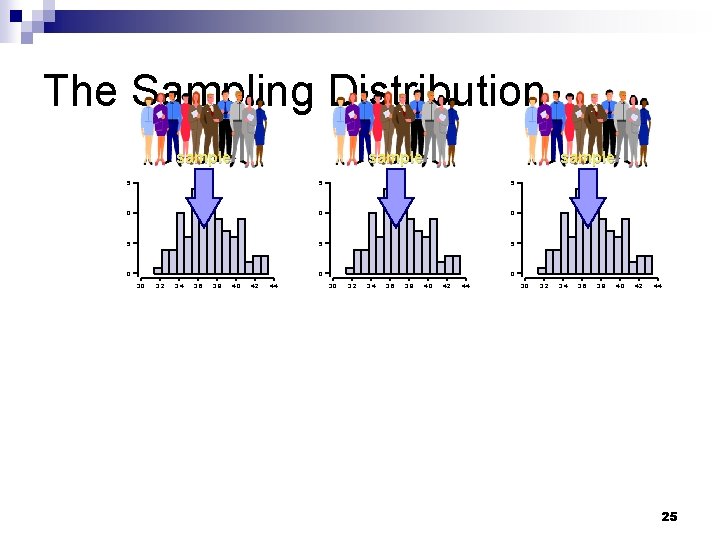
The Sampling Distribution sample 5 5 5 0 0 0 3. 2 3. 4 3. 6 3. 8 4. 0 4. 2 4. 4 3. 0 3. 2 3. 4 3. 6 3. 8 4. 0 4. 2 4. 4 25

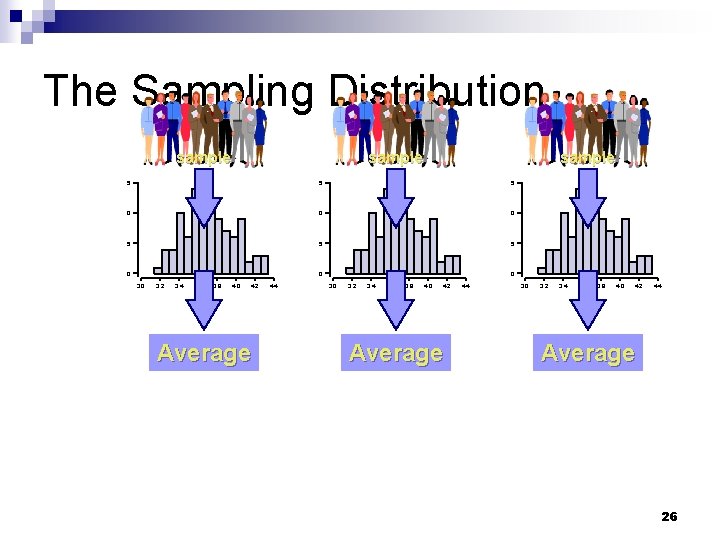
The Sampling Distribution sample 5 5 5 0 0 0 3. 2 3. 4 3. 6 3. 8 4. 0 4. 2 Average 4. 4 3. 0 3. 2 3. 4 3. 6 3. 8 4. 0 4. 2 4. 4 Average 26

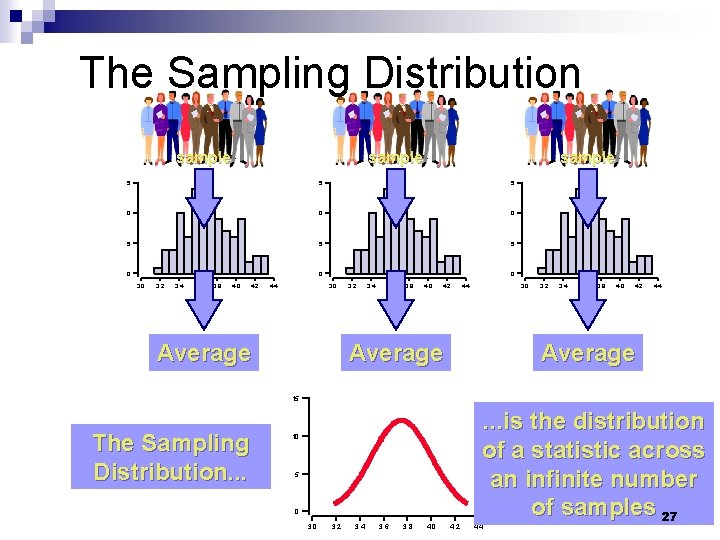
The Sampling Distribution sample 5 5 5 0 0 0 3. 2 3. 4 3. 6 3. 8 4. 0 4. 2 4. 4 3. 0 Average 3. 2 3. 4 3. 6 3. 8 4. 0 4. 2 4. 4 Average 15 The Sampling Distribution. . . 10 5 0 3. 2 3. 4 3. 6 3. 8 4. 0 4. 2 . . . is the distribution of a statistic across an infinite number of samples 27 4. 4

Random Sampling 28

Types of Probability Sampling Designs Simple Random Sampling n Stratified Sampling n Systematic Sampling n Cluster Sampling n Multistage Sampling n 29

Some Definitions N = the number of cases in the sampling frame n n = the number of cases in the sample n NCn = the number of combinations (subsets) of n from N n f = n/N = the sampling fraction n 30

Simple Random Sampling • Objective - select n units out of N such that every NCn has an equal chance • Procedure - use table of random numbers, computer random number generator or mechanical device • can sample with or without replacement • f=n/N is the sampling fraction 31

Simple Random Sampling Example: People who subscribe Novin Pezeshki last year n People who visit our site n draw a simple random sample of n/N n 32

Simple Random Sampling List of Residents 33

Simple Random Sampling List of Residents Random Subsample 34

Stratified Random Sampling • sometimes called "proportional" or "quota" random sampling • Objective - population of N units divided into non-overlapping strata N 1, N 2, N 3, . . . Ni such that N 1 + N 2 +. . . + Ni = N, then do simple random sample of n/N in each strata 35

n Stratified Sampling The population is first divided into groups called strata. If stratification is evident ¨ n n n Example: medical students; preclinical, clerckship, internship Best results when low intra strata variance and high inter strata variance A simple random sample is taken from each stratum. Advantage: If strata are homogeneous, this method is “more precise” than simple random sampling of same sample size As precise but with a smaller total sample size. If there is a dominant strata and it is relatively small, you can enumerate it, and sample the rest. 36

Stratified Sampling - Purposes: • to insure representation of each strata - oversample smaller population groups • sampling problems may differ in each strata • increase precision (lower variance) if strata are homogeneous within (like blocking) 37

Stratified Random Sampling List of Residents 38

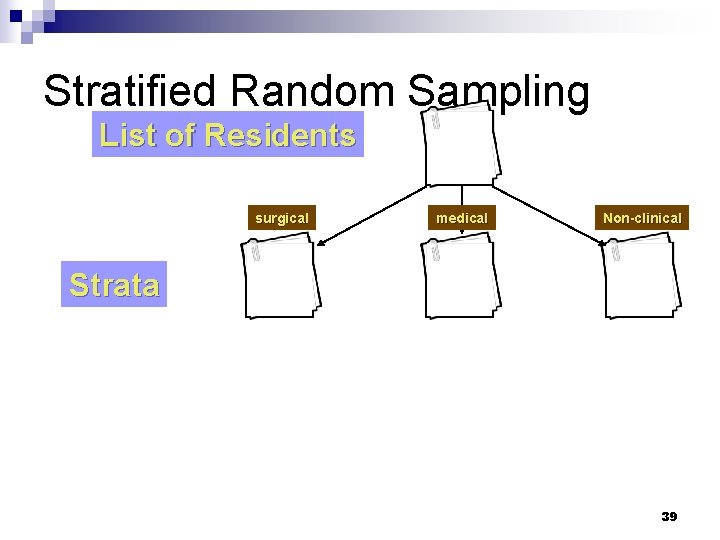
Stratified Random Sampling List of Residents surgical medical Non-clinical Strata 39

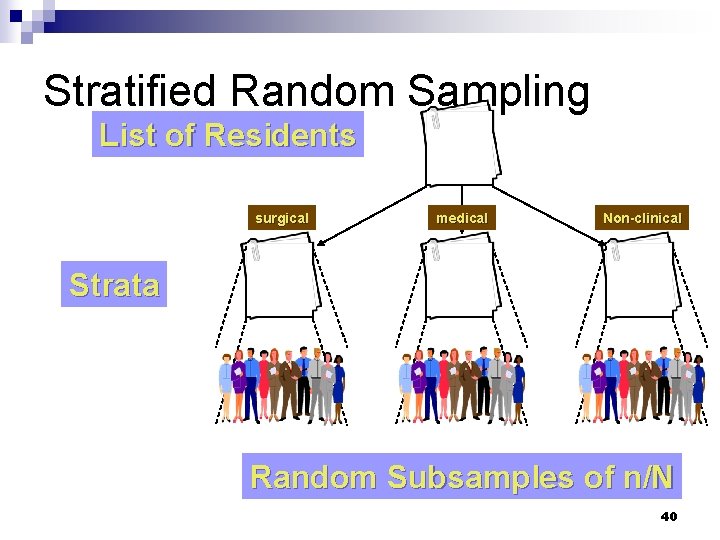
Stratified Random Sampling List of Residents surgical medical Non-clinical Strata Random Subsamples of n/N 40

Systematic Random Sampling Procedure: number units in population from 1 to N n decide on the n that you want or need n N/n=k the interval size n randomly select a number from 1 to k n then take every kth unit n 41

Systematic Random Sampling Assumes that the population is randomly ordered n Advantages - easy; may be more precise than simple random sample n Example - Residents study n 42

Systematic Random Sampling N = 100 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 43

Systematic Random Sampling N = 100 want n = 20 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 44

Systematic Random Sampling N = 100 want n = 20 N/n = 5 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 45

Systematic Random Sampling N = 100 want n = 20 N/n = 5 select a random number from 1 -5: chose 4 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 46

Systematic Random Sampling N = 100 want n = 20 N/n = 5 select a random number from 1 -5: chose 4 start with #4 and take every 5 th unit 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 47

Cluster Sampling n The population is first divided into clusters n A cluster is a small-scale version of the population (i. e. heterogeneous group reflecting the variance in the population. n Take a simple random sample of the clusters. n All elements within each sampled (chosen) cluster form the sample. 48

Cluster Random Sampling Advantages - administratively useful, especially when you have a wide geographic area to cover n Example: Randomly sample from city blocks and measure all homes in selected blocks n 49

Cluster Sampling vs. Stratified Sampling n Stratified sampling seeks to divide the sample into heterogeneous groups so the variance within the strata is low and between the strata is high. n Cluster sampling seeks to have each cluster reflect the variance in the population…each cluster is a “mini” population. Each cluster is a mirror of the total population and of each other. 50

Multi-Stage Sampling Cluster random sampling can be multistage n Any combinations of single-stage methods n 51

Multi-Stage Sampling choosing � choosing students from medical schools: Select all schools, then sample within schools n Sample schools, then measure all students n Sample schools, then sample students n 52

Nonrandom Sampling Designs 53

Types of nonrandom samples Accidental, haphazard, convenience n Modal Instance n Purposive n Expert n Quota n Snowball n Heterogeneity sampling n 54

Accidental or Haphazard Sampling “Man on the street” n Medical student in the library n available or accessible clients n volunteer samples • Problem: we have no evidence for representativeness n 55

Convenience Sampling ¨ The sample is identified primarily by convenience. n It is a nonprobability sampling technique. Items are included in the sample without known probabilities of being selected. n Example: A professor conducting research might use student volunteers to constitute a sample. 56

Convenience Sampling Advantage: Relatively easy, fast, often, but not always, cheap n Disadvantage: It is impossible to determine how representative of the population the sample is. n ¨ Try to offset this by collecting large sample size. 57

Quota Sampling n select people nonrandomly according to some quotas 61

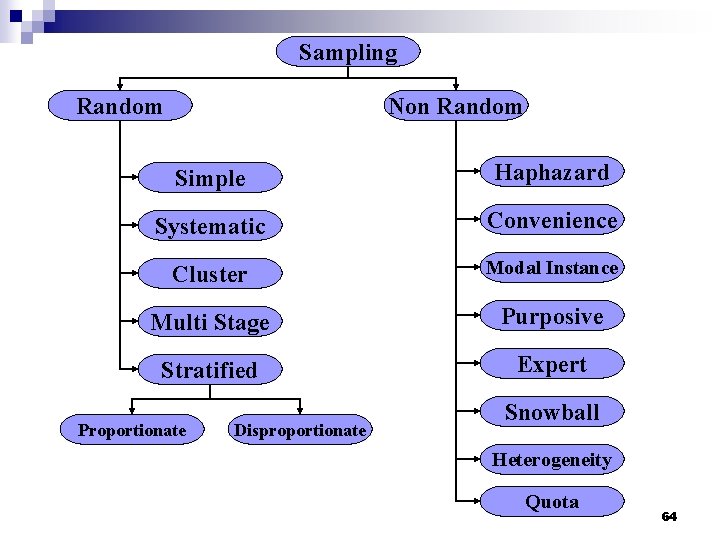
Sampling Random Non Random Simple Haphazard Systematic Convenience Cluster Modal Instance Multi Stage Purposive Stratified Expert Proportionate Disproportionate Snowball Heterogeneity Quota 64

65