Chapter Eleven Sampling Design and Procedures Copyright 2010






























- Slides: 42

Chapter Eleven Sampling: Design and Procedures Copyright © 2010 Pearson Education, Inc. 11 -1

Chapter Outline 1) Overview 2) Sample or Census 3) The Sampling Design Process i. Define the Target Population ii. Determine the Sampling Frame iii. Select a Sampling Technique iv. Determine the Sample Size v. Execute the Sampling Process Copyright © 2010 Pearson Education, Inc. 11 -2

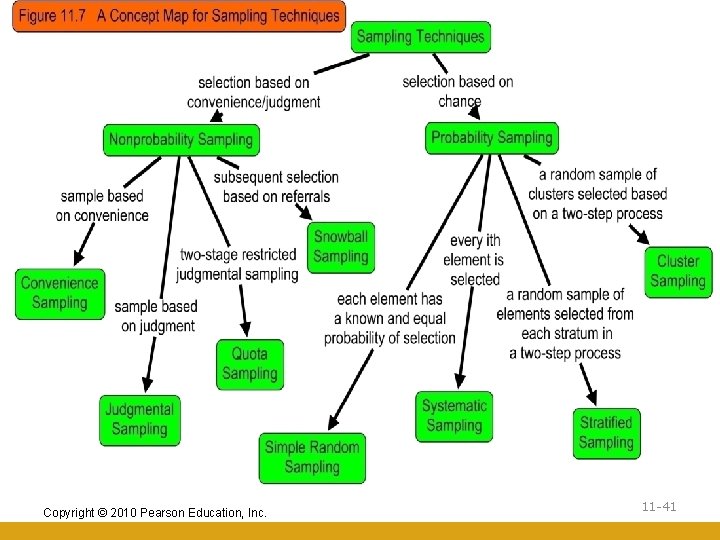
Chapter Outline 4) A Classification of Sampling Techniques i. Nonprobability Sampling Techniques a. Convenience Sampling b. Judgmental Sampling c. Quota Sampling d. Snowball Sampling ii. Probability Sampling Techniques a. Simple Random Sampling b. Systematic Sampling c. Stratified Sampling d. Cluster Sampling e. Other Probability Sampling Techniques Copyright © 2010 Pearson Education, Inc. 11 -3

Chapter Outline 5) Choosing Nonprobability Versus Probability Sampling 6) Uses of Nonprobability Versus Probability Sampling 7) Internet Sampling 8) International Marketing Research 9) Ethics in Marketing Research 10)Summary Copyright © 2010 Pearson Education, Inc. 11 -4

Sample Vs. Census Table 11. 1 Copyright © 2010 Pearson Education, Inc. 11 -5

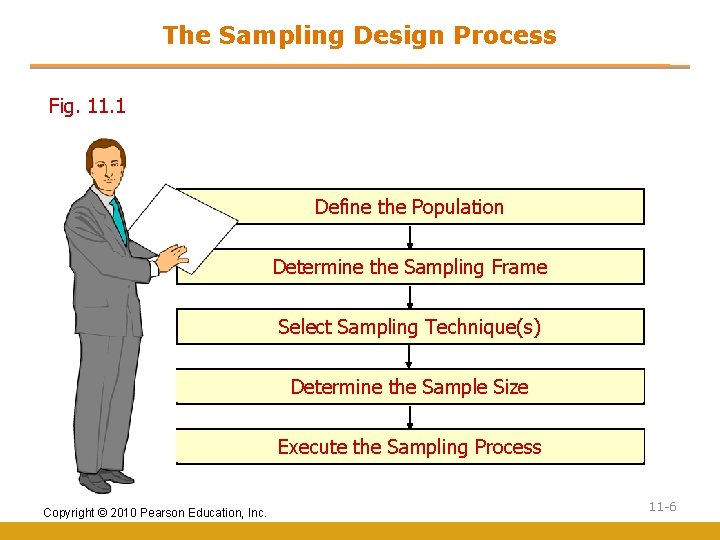
The Sampling Design Process Fig. 11. 1 Define the Population Determine the Sampling Frame Select Sampling Technique(s) Determine the Sample Size Execute the Sampling Process Copyright © 2010 Pearson Education, Inc. 11 -6

Define the Target Population The target population is the collection of elements or objects that possess the information sought by the researcher and about which inferences are to be made. The target population should be defined in terms of elements, sampling units, extent, and time. • An element is the object about which or from which the information is desired, e. g. , the respondent. • A sampling unit is an element, or a unit containing the element, that is available for selection at some stage of the sampling process. • Extent refers to the geographical boundaries. • Time is the time period under consideration. Copyright © 2010 Pearson Education, Inc. 11 -7

Define the Target Population Important qualitative factors in determining the sample size are: • • the importance of the decision the nature of the research the number of variables the nature of the analysis sample sizes used in similar studies incidence rates completion rates resource constraints Copyright © 2010 Pearson Education, Inc. 11 -8

Sample Sizes Used in Marketing Research Studies Table 11. 2 Copyright © 2010 Pearson Education, Inc. 11 -9

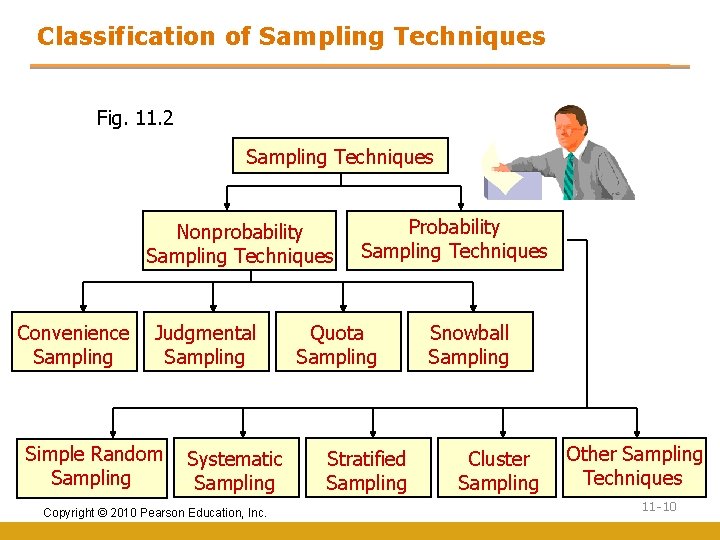
Classification of Sampling Techniques Fig. 11. 2 Sampling Techniques Nonprobability Sampling Techniques Convenience Sampling Judgmental Sampling Simple Random Sampling Systematic Sampling Copyright © 2010 Pearson Education, Inc. Probability Sampling Techniques Quota Sampling Stratified Sampling Snowball Sampling Cluster Sampling Other Sampling Techniques 11 -10

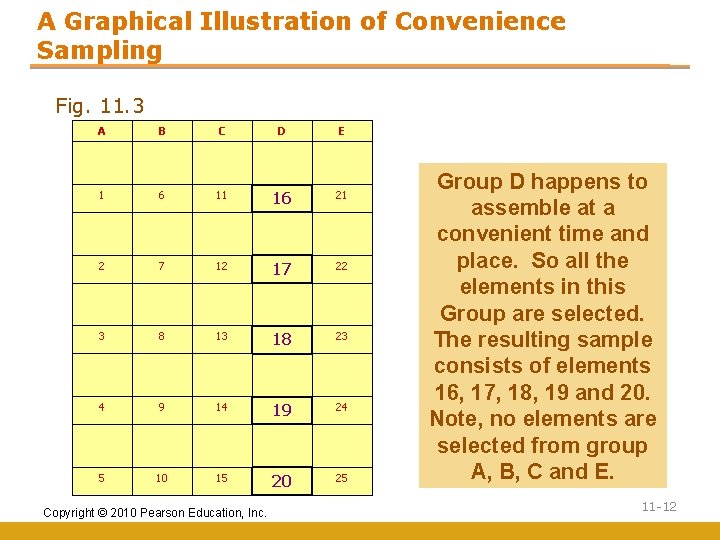
Convenience Sampling Convenience sampling attempts to obtain a sample of convenient elements. Often, respondents are selected because they happen to be in the right place at the right time. • Use of students, and members of social organizations • Mall intercept interviews without qualifying the respondents • Department stores using charge account lists • “People on the street” interviews Copyright © 2010 Pearson Education, Inc. 11 -11

A Graphical Illustration of Convenience Sampling Fig. 11. 3 A 11. 3 B C D E 1 6 11 16 21 2 7 12 17 22 3 8 13 18 23 4 9 14 19 24 5 10 15 20 25 Copyright © 2010 Pearson Education, Inc. Group D happens to assemble at a convenient time and place. So all the elements in this Group are selected. The resulting sample consists of elements 16, 17, 18, 19 and 20. Note, no elements are selected from group A, B, C and E. 11 -12

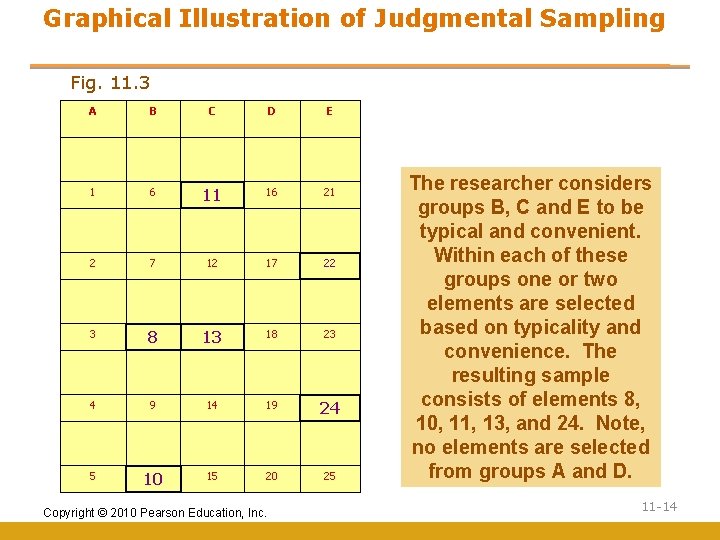
Judgmental Sampling Judgmental sampling is a form of convenience sampling in which the population elements are selected based on the judgment of the researcher. • Test markets • Purchase engineers selected in industrial marketing research • Bellwether precincts selected in voting behavior research • Expert witnesses used in court Copyright © 2010 Pearson Education, Inc. 11 -13

Graphical Illustration of Judgmental Sampling Fig. 11. 3 A B C D E 1 6 11 16 21 2 7 12 17 22 3 8 13 18 23 4 9 14 19 24 5 10 15 20 25 Copyright © 2010 Pearson Education, Inc. The researcher considers groups B, C and E to be typical and convenient. Within each of these groups one or two elements are selected based on typicality and convenience. The resulting sample consists of elements 8, 10, 11, 13, and 24. Note, no elements are selected from groups A and D. 11 -14

Quota Sampling Quota sampling may be viewed as two-stage restricted judgmental sampling. • The first stage consists of developing control categories, or quotas, of population elements. • In the second stage, sample elements are selected based on convenience or judgment. Control Variable Sex Male Female Population composition Sample composition Percentage Number 48 52 ____ 100 Copyright © 2010 Pearson Education, Inc. 48 52 ____ 100 480 520 ____ 1000 11 -15

A Graphical Illustration of Quota Sampling Fig. 11. 3 A B C D E 1 6 11 16 21 2 7 12 17 22 3 8 13 18 23 4 9 14 19 24 5 10 15 20 25 Copyright © 2010 Pearson Education, Inc. A quota of one element from each group, A to E, is imposed. Within each group, one element is selected based on judgment or convenience. The resulting sample consists of elements 3, 6, 13, 20 and 22. Note, one element is selected from each column or group. 11 -16

Snowball Sampling In snowball sampling, an initial group of respondents is selected, usually at random. • After being interviewed, these respondents are asked to identify others who belong to the target population of interest. • Subsequent respondents are selected based on the referrals. Copyright © 2010 Pearson Education, Inc. 11 -17

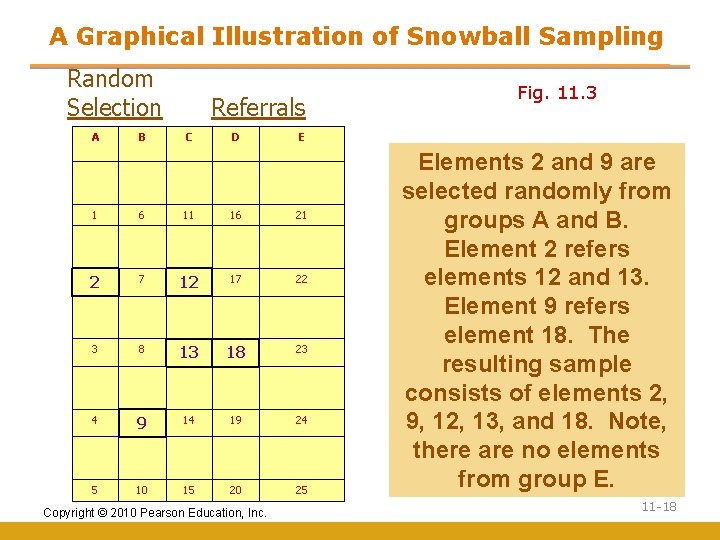
A Graphical Illustration of Snowball Sampling Random Selection A B Referrals C D E 1 6 11 16 21 2 7 12 17 22 3 8 13 18 23 4 9 14 19 24 5 10 15 20 25 Copyright © 2010 Pearson Education, Inc. Fig. 11. 3 Elements 2 and 9 are selected randomly from groups A and B. Element 2 refers elements 12 and 13. Element 9 refers element 18. The resulting sample consists of elements 2, 9, 12, 13, and 18. Note, there are no elements from group E. 11 -18

Simple Random Sampling • Each element in the population has a known and equal probability of selection. • Each possible sample of a given size (n) has a known and equal probability of being the sample actually selected. • This implies that every element is selected independently of every other element. Copyright © 2010 Pearson Education, Inc. 11 -19

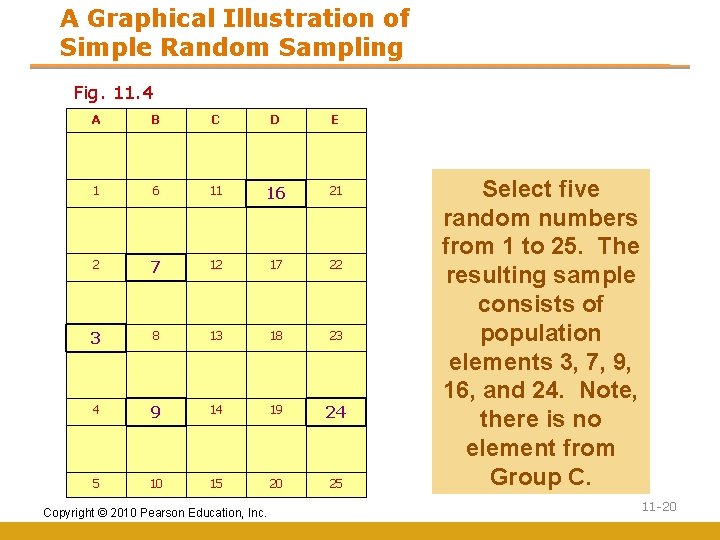
A Graphical Illustration of Simple Random Sampling Fig. 11. 4 A B C D E 1 6 11 16 21 2 7 12 17 22 3 8 13 18 23 4 9 14 19 24 5 10 15 20 25 Copyright © 2010 Pearson Education, Inc. Select five random numbers from 1 to 25. The resulting sample consists of population elements 3, 7, 9, 16, and 24. Note, there is no element from Group C. 11 -20

Systematic Sampling • The sample is chosen by selecting a random starting point and then picking every ith element in succession from the sampling frame. • The sampling interval, i, is determined by dividing the population size N by the sample size n and rounding to the nearest integer. • When the ordering of the elements is related to the characteristic of interest, systematic sampling increases the representativeness of the sample. Copyright © 2010 Pearson Education, Inc. 11 -21

Systematic Sampling • If the ordering of the elements produces a cyclical pattern, systematic sampling may decrease the representativeness of the sample. For example, there are 100, 000 elements in the population and a sample of 1, 000 is desired. In this case the sampling interval, i, is 100. A random number between 1 and 100 is selected. If, for example, this number is 23, the sample consists of elements 23, 123, 223, 323, 423, 523, and so on. Copyright © 2010 Pearson Education, Inc. 11 -22

A Graphical Illustration of Systematic Sampling Fig. 11. 4 A B C D E 1 6 11 16 21 2 7 12 17 22 3 8 13 18 23 4 9 14 19 24 5 10 15 20 25 Copyright © 2010 Pearson Education, Inc. Select a random number between 1 and 5, say 2. The resulting sample consists of population 2, (2+5=) 7, (2+5 x 2=) 12, (2+5 x 3=)17, and (2+5 x 4=) 22. Note, all the elements are selected from a single row. 11 -23

Stratified Sampling • A two-step process in which the population is partitioned into subpopulations, or strata. • The strata should be mutually exclusive and collectively exhaustive in that every population element should be assigned to one and only one stratum and no population elements should be omitted. • Next, elements are selected from each stratum by a random procedure, usually SRS. • A major objective of stratified sampling is to increase precision without increasing cost. Copyright © 2010 Pearson Education, Inc. 11 -24

Stratified Sampling • The elements within a stratum should be as homogeneous as possible, but the elements in different strata should be as heterogeneous as possible. • The stratification variables should also be closely related to the characteristic of interest. • Finally, the variables should decrease the cost of the stratification process by being easy to measure and apply. Copyright © 2010 Pearson Education, Inc. 11 -25

Stratified Sampling • In proportionate stratified sampling, the size of the sample drawn from each stratum is proportionate to the relative size of that stratum in the total population. • In disproportionate stratified sampling, the size of the sample from each stratum is proportionate to the relative size of that stratum and to the standard deviation of the distribution of the characteristic of interest among all the elements in that stratum. Copyright © 2010 Pearson Education, Inc. 11 -26

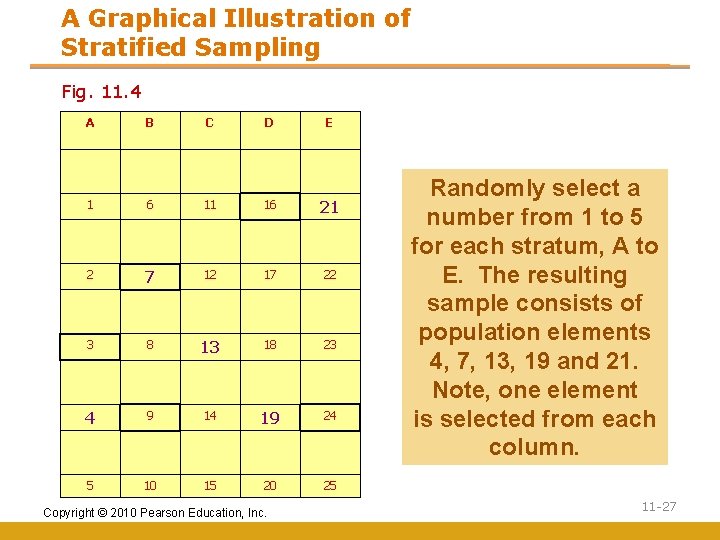
A Graphical Illustration of Stratified Sampling Fig. 11. 4 A B C D 1 6 11 16 21 2 7 12 17 22 3 8 13 18 23 4 9 14 19 24 5 10 15 20 25 Copyright © 2010 Pearson Education, Inc. E Randomly select a number from 1 to 5 for each stratum, A to E. The resulting sample consists of population elements 4, 7, 13, 19 and 21. Note, one element is selected from each column. 11 -27

Cluster Sampling • The target population is first divided into mutually exclusive and collectively exhaustive subpopulations, or clusters. • Then a random sample of clusters is selected, based on a probability sampling technique such as SRS. • For each selected cluster, either all the elements are included in the sample (onestage) or a sample of elements is drawn probabilistically (two-stage). Copyright © 2010 Pearson Education, Inc. 11 -28

Cluster Sampling • Elements within a cluster should be as heterogeneous as possible, but clusters themselves should be as homogeneous as possible. Ideally, each cluster should be a small-scale representation of the population. • In probability proportionate to size sampling, the clusters are sampled with probability proportional to size. In the second stage, the probability of selecting a sampling unit in a selected cluster varies inversely with the size of the cluster. Copyright © 2010 Pearson Education, Inc. 11 -29

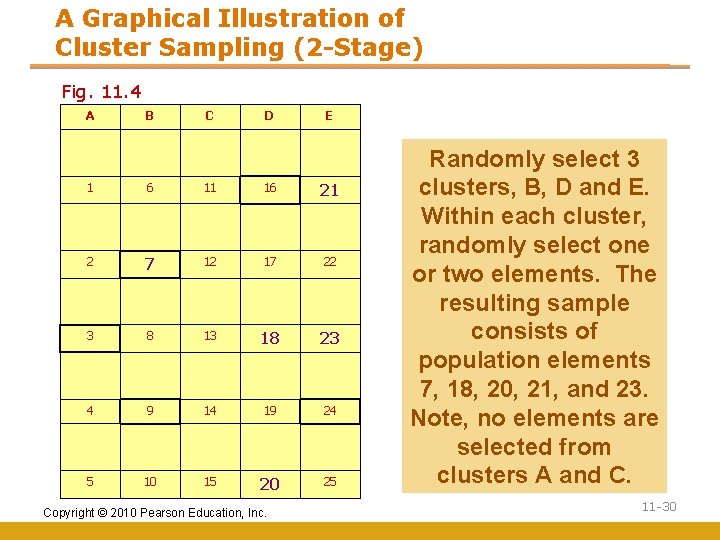
A Graphical Illustration of Cluster Sampling (2 -Stage) Fig. 11. 4 A B C D E 1 6 11 16 21 2 7 12 17 22 3 8 13 18 23 4 9 14 19 24 5 10 15 20 25 Copyright © 2010 Pearson Education, Inc. Randomly select 3 clusters, B, D and E. Within each cluster, randomly select one or two elements. The resulting sample consists of population elements 7, 18, 20, 21, and 23. Note, no elements are selected from clusters A and C. 11 -30

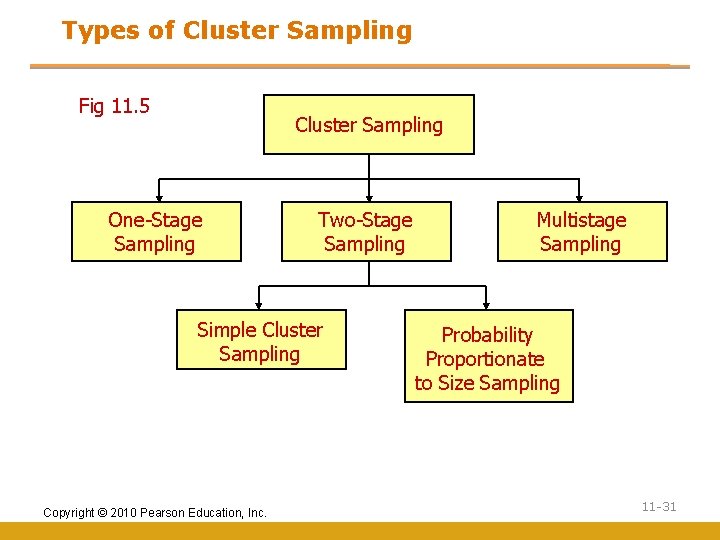
Types of Cluster Sampling Fig 11. 5 Cluster Sampling One-Stage Sampling Two-Stage Sampling Simple Cluster Sampling Copyright © 2010 Pearson Education, Inc. Multistage Sampling Probability Proportionate to Size Sampling 11 -31

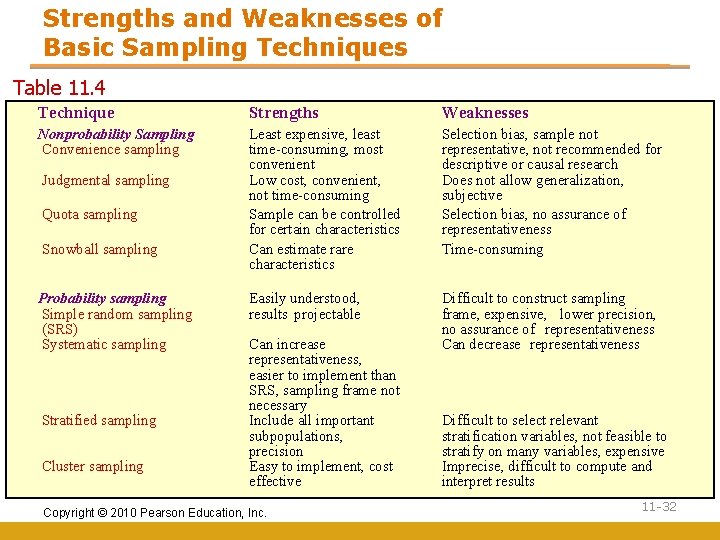
Strengths and Weaknesses of Basic Sampling Techniques Table 11. 4 Technique Strengths Weaknesses Nonprobability Sampling Convenience sampling Least expensive, least time-consuming, most convenient Low cost, convenient, not time-consuming Sample can be controlled for certain characteristics Can estimate rare characteristics Selection bias, sample not representative, not recommended for descriptive or causal research Does not allow generalization, subjective Selection bias, no assurance of representativeness Time-consuming Easily understood, results projectable Difficult to construct sampling frame, expensive, lower precision, no assurance of representativeness Can decrease representativeness Judgmental sampling Quota sampling Snowball sampling Probability sampling Simple random sampling (SRS) Systematic sampling Stratified sampling Cluster sampling Can increase representativeness, easier to implement than SRS, sampling frame not necessary Include all important subpopulations, precision Easy to implement, cost effective Copyright © 2010 Pearson Education, Inc. Difficult to select relevant stratification variables, not feasible to stratify on many variables, expensive Imprecise, difficult to compute and interpret results 11 -32

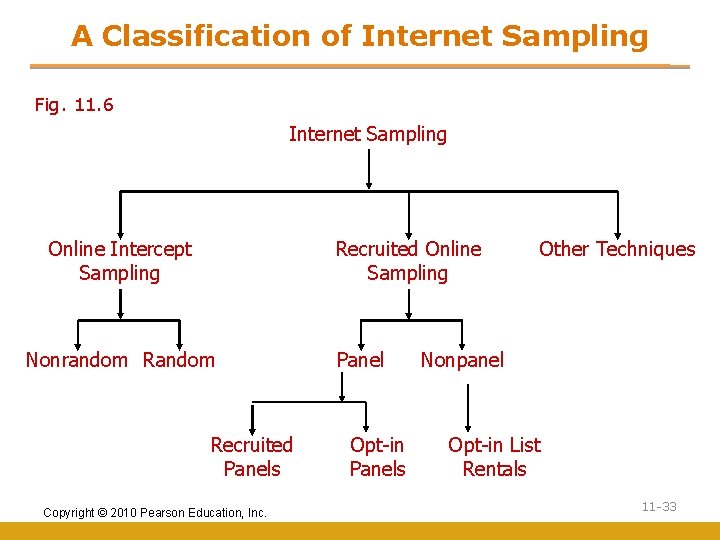
A Classification of Internet Sampling Fig. 11. 6 Internet Sampling Online Intercept Sampling Recruited Online Sampling Nonrandom Recruited Panels Copyright © 2010 Pearson Education, Inc. Panel Opt-in Panels Other Techniques Nonpanel Opt-in List Rentals 11 -33

Procedures for Drawing Probability Samples Exhibit 11. 1 Simple Random Sampling 1. Select a suitable sampling frame. 2. Each element is assigned a number from 1 to N (pop. size). 3. Generate n (sample size) different random numbers between 1 and N. 4. The numbers generated denote the elements that should be included in the sample. Copyright © 2010 Pearson Education, Inc. 11 -34

Procedures for Drawing Probability Samples Exhibit 11. 1, cont. Systematic Sampling 1. Select a suitable sampling frame. 2. Each element is assigned a number from 1 to N (pop. size). 3. Determine the sampling interval i: i=N/n. If i is a fraction, round to the nearest integer. 4. Select a random number, r, between 1 and i, as explained in simple random sampling. 5. The elements with the following numbers will comprise the systematic random sample: r, r+i, r+2 i, r+3 i, r+4 i, . . . , r+(n-1)i. Copyright © 2010 Pearson Education, Inc. 11 -35

Procedures for Drawing Probability Samples Stratified Sampling Exhibit 11. 1, cont. 1. Select a suitable frame. 2. Select the stratification variable(s) and the number of strata, H. 3. Divide the entire population into H strata. Based on the classification variable, each element of the population is assigned to one of the H strata. 4. In each stratum, number the elements from 1 to Nh (the pop. size of stratum h). 5. Determine the sample size of each stratum, nh, based on proportionate or disproportionate stratified sampling, where H h=1 nh = n 6. In each stratum, select a simple random sample of size nh Copyright © 2010 Pearson Education, Inc. 11 -36

Procedures for Drawing Probability Samples Cluster Sampling Exhibit 11. 1, cont. 1. Assign a number from 1 to N to each element in the population. 2. Divide the population into C clusters of which c will be included in the sample. 3. Calculate the sampling interval i, i=N/c (round to nearest integer). 4. Select a random number r between 1 and i, as explained in simple random sampling. 5. Identify elements with the following numbers: r, r+i, r+2 i, . . . r+(c-1)i. 6. Select the clusters that contain the identified elements. 7. Select sampling units within each selected cluster based on SRS or systematic sampling. 8. Remove clusters exceeding sampling interval i. Calculate new population size N*, number of clusters to be selected c*= c-1, and new sampling interval i*. Copyright © 2010 Pearson Education, Inc. 11 -37

Procedures for Drawing Probability Samples Exhibit 11. 1, cont. Cluster Sampling Repeat the process until each of the remaining clusters has a population less than the sampling interval. If b clusters have been selected with certainty, select the remaining c-b clusters according to steps 1 through 7. The fraction of units to be sampled with certainty is the overall sampling fraction = n/N. Thus, for clusters selected with certainty, we would select ns=(n/N)(N 1+N 2+. . . +Nb) units. The units selected from clusters selected under two-stage sampling will therefore be n*=n-ns. Copyright © 2010 Pearson Education, Inc. 11 -38

Choosing Nonprobability Vs. Probability Sampling Table 11. 4 Copyright © 2010 Pearson Education, Inc. 11 -39

Tennis' Systematic Sampling Returns a Smash Tennis magazine conducted a mail survey of its subscribers to gain a better understanding of its market. Systematic sampling was employed to select a sample of 1, 472 subscribers from the publication's domestic circulation list. If we assume that the subscriber list had 1, 472, 000 names, the sampling interval would be 1, 000 (1, 472, 000/1, 472). A number from 1 to 1, 000 was drawn at random. Beginning with that number, every 1, 000 th subscriber was selected. A brand-new dollar bill was included with the questionnaire as an incentive to respondents. An alert postcard was mailed one week before the survey. A second, follow-up, questionnaire was sent to the whole sample ten days after the initial questionnaire. There were 76 post office returns, so the net effective mailing was 1, 396. Six weeks after the first mailing, 778 completed questionnaires were returned, yielding a response rate of 56%. Copyright © 2010 Pearson Education, Inc. 11 -40

Copyright © 2010 Pearson Education, Inc. 11 -41

All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior written permission of the publisher. Printed in the United States of America. Copyright © 2010 Pearson Education, Inc. publishing as Prentice Hall Copyright © 2010 Pearson Education, Inc. 11 -42