Lecture 4 Sampling Overview of Sampling Theory Sampling

Sampling Continuous Signals n n n Sample Period is T, Frequency is 1/T x[n]

Continuous-time Sampling n Delta function d(t) n n Zero everywhere except t=0 Integral of

Continuous-time Sampling n Defining the sequence by multiple sifts: n Equivalently: n Note: xa(t)

Reconstruction n Given a train of samples – how to rebuild a continuous-time signal?

Example Linear interpolation: Integral (0, 2) of imp(t) = 1 Imp(t) = 0 at

DAC Output n n Stair-step output DAC needs filtering to reduce excess high frequency

Sinc(x) – ‘Perfect Reconstruction’ n n Is there an impulse function which needs no

Perfect Reconstruction II n Note – Sinc(t) is non-zero for all t n n

Operations on sequences n n n Addition: Scaling: Modulation: n n Windowing is a

Resampling (Integer Case) n Suppose we have x[n] sampled at T 1 but want

Sampling Theorem n Perfect Reconstruction of a continuoustime signal with Bandlimit f requires samples

Alaising n n For Sinusoid signals (natural bandlimit): For Cos(wn), w=2 pk+w 0 n

Slides: 16

Download presentation

Lecture 4 Sampling Overview of Sampling Theory

Sampling Continuous Signals n n n Sample Period is T, Frequency is 1/T x[n] = xa(n) = x(t)|t=n. T Samples of x(t) from an infinite discrete sequence

Continuous-time Sampling n Delta function d(t) n n Zero everywhere except t=0 Integral of d(t) over any interval including t=0 is 1 (Not a function – but the limit of functions) Sifting

Continuous-time Sampling n Defining the sequence by multiple sifts: n Equivalently: n Note: xa(t) is not defined at t=n. T and is zero for other t

Reconstruction n Given a train of samples – how to rebuild a continuous-time signal? In general, Convolve some impluse function with the samples: Imp(t) can be any function with unit integral…

Example Linear interpolation: Integral (0, 2) of imp(t) = 1 Imp(t) = 0 at t=0, 2 Reconstucted function is piecewise-linear interpolation of sample values

DAC Output n n Stair-step output DAC needs filtering to reduce excess high frequency information

Sinc(x) – ‘Perfect Reconstruction’ n n Is there an impulse function which needs no filtering? Why? – Remember that Sin(t)/t is Fourier Transform of a unit impulse

Perfect Reconstruction II n Note – Sinc(t) is non-zero for all t n n Implies that all samples (including negative time) are needed Note that x(t) is defined for all t since Sinc(0)=1

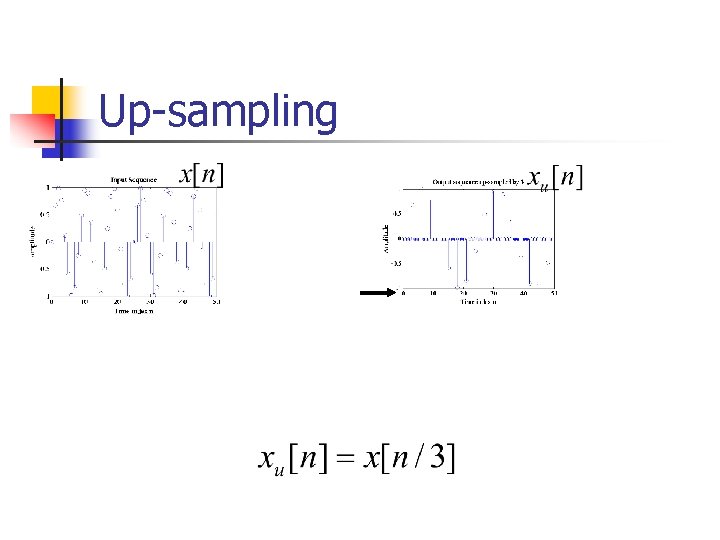
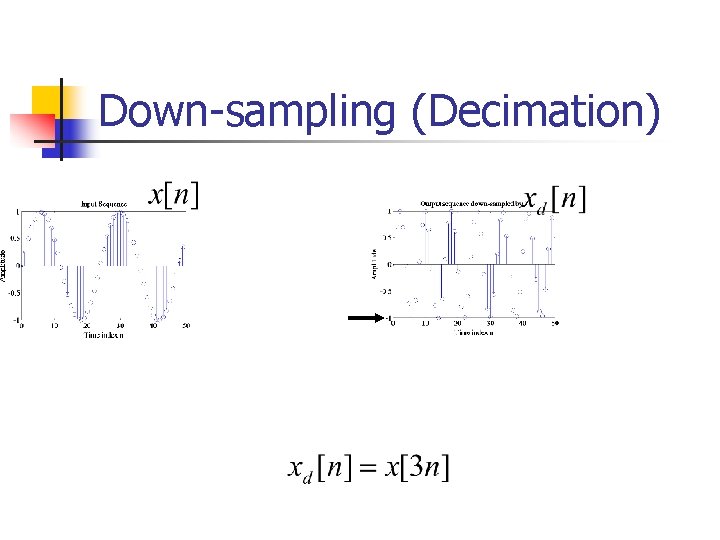
Operations on sequences n n n Addition: Scaling: Modulation: n n Windowing is a type of modulation Time-Shift: Up-sampling: Down-sampling:

Up-sampling

Down-sampling (Decimation)

Resampling (Integer Case) n Suppose we have x[n] sampled at T 1 but want x. R[n] sampled at T 2=L T 1

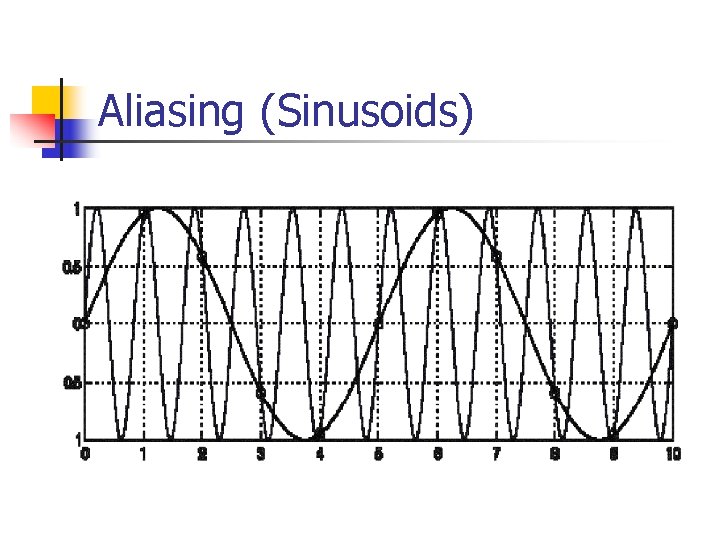
Sampling Theorem n Perfect Reconstruction of a continuoustime signal with Bandlimit f requires samples no longer than 1/2 f n n Bandlimit is not Bandwidth – but limit of maximum frequency Any signal beyond f aliases the samples

Aliasing (Sinusoids)

Alaising n n For Sinusoid signals (natural bandlimit): For Cos(wn), w=2 pk+w 0 n n Samples for all k are the same! Unambiguous if 0<w<p Thus One-half cycle per sample So if sampling at T, frequencies of f=e+1/2 T will map to frequency e