Sampling Sampling Distributions Sampling vs Census Reasons for

Sampling & Sampling Distributions Sampling vs Census Reasons for Taking a Sample: 1) Save Time 2) Save Money 3) Infinite Population 4) Destructive Testing 5) More Accurate Sampling Error - Sample Does Not Reflect the Population by Random Chance.

Sampling Bias – Sample Does Not Reflect the Population because Certain Elements of the Population have a Higher Chance of Selection. Literary Digest Poll – 1936 Roosevelt Landon 972, 897 1, 293, 669 Bias of Non-Response Taking a Random Sample will Prevent Sampling Bias. Simple Random Sample – Each Element of the Population has equal Chance of Selection.

Ex: Simple Random Sample Select 3 people from 8 people 1) Mary 2) Joni 3) Neil 4) Don 5) Linda 6) Paul 7) Mark 8) Jane Random Number Table

Modifications of Simple Random Sampling: Systematic Random Sample – A Few Random Selections Force the other Selections Stratified Random Sample – Divide Population into Strata Cluster Sampling – Divide Population into Clusters (Areas)
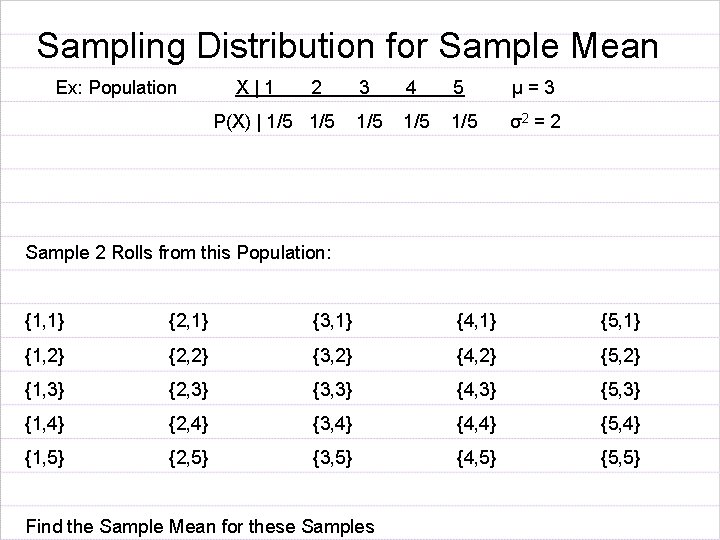
Sampling Distribution for Sample Mean Ex: Population X|1 2 P(X) | 1/5 3 4 5 µ=3 1/5 1/5 σ2 = 2 Sample 2 Rolls from this Population: {1, 1} {2, 1} {3, 1} {4, 1} {5, 1} {1, 2} {2, 2} {3, 2} {4, 2} {5, 2} {1, 3} {2, 3} {3, 3} {4, 3} {5, 3} {1, 4} {2, 4} {3, 4} {4, 4} {5, 4} {1, 5} {2, 5} {3, 5} {4, 5} {5, 5} Find the Sample Mean for these Samples
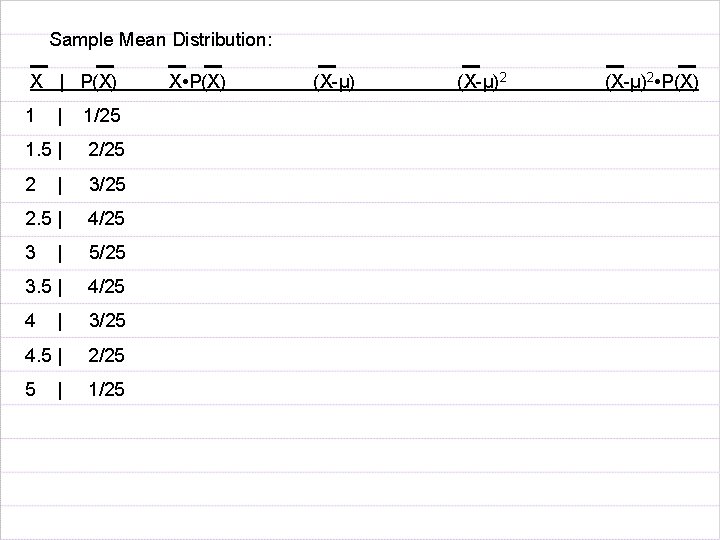
Sample Mean Distribution: X | P(X) 1 | 1/25 1. 5 | 2/25 2 | 3/25 2. 5 | 4/25 3 | 5/25 3. 5 | 4/25 4 | 3/25 4. 5 | 2/25 5 1/25 | X • P(X) (X-µ)2 • P(X)
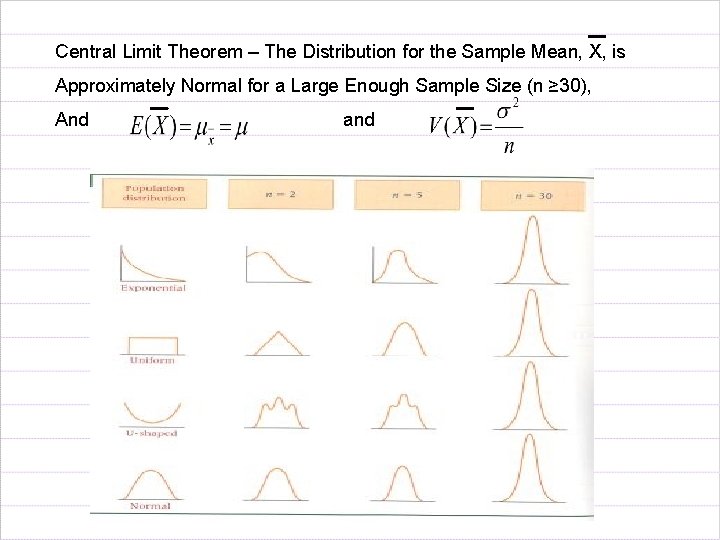
Central Limit Theorem – The Distribution for the Sample Mean, X, is Approximately Normal for a Large Enough Sample Size (n ≥ 30), And and

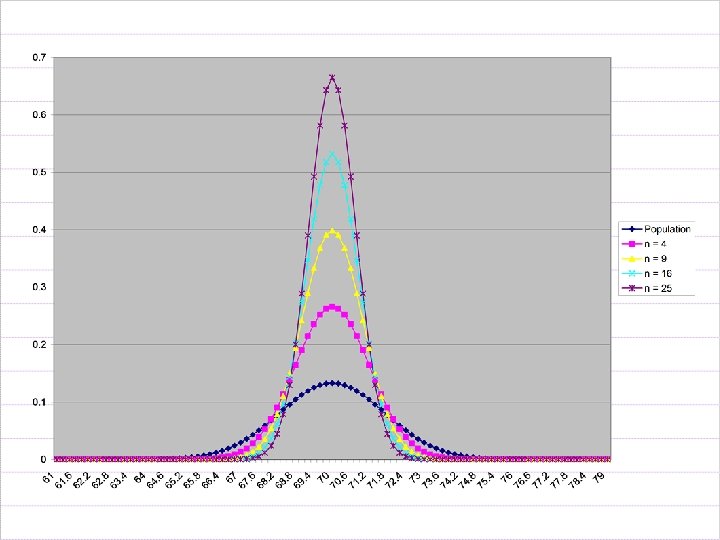
Z Formula for Sample Mean Transformation to Standardized Normal Curve Ex: Male Heights are Normally Distributed with a Mean of 70” Std Dev of 3” P(X > 72”) = If n = 4, P( > 72”) =

n =25 P( > 72)

Sampling from a Finite Population • Finite Correction Factor • Modified Z Formula Use If n >. 05 • N
- Slides: 11