Hypothesis and Hypothesis Testing HYPOTHESIS A statement about

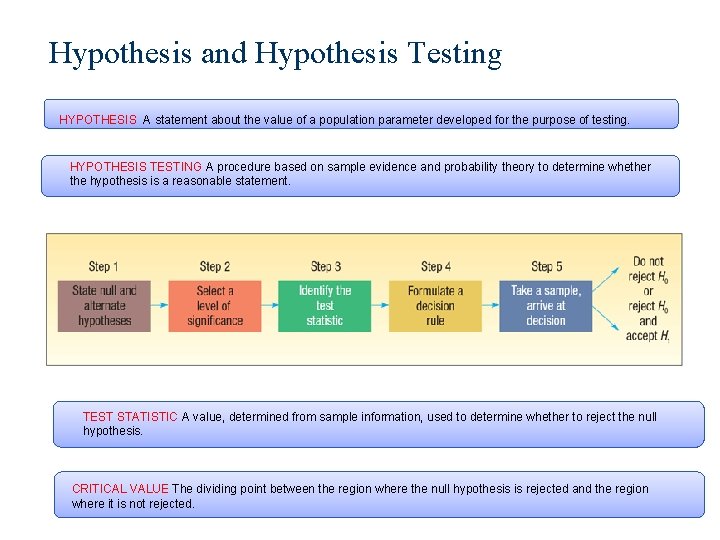
Hypothesis and Hypothesis Testing HYPOTHESIS A statement about the value of a population parameter developed for the purpose of testing. HYPOTHESIS TESTING A procedure based on sample evidence and probability theory to determine whether the hypothesis is a reasonable statement. TEST STATISTIC A value, determined from sample information, used to determine whether to reject the null hypothesis. CRITICAL VALUE The dividing point between the region where the null hypothesis is rejected and the region where it is not rejected.

Important Things to Remember about H 0 and H 1 n n n n n H 0: null hypothesis and H 1: alternate hypothesis H 0 and H 1 are mutually exclusive and collectively exhaustive H 0 is always presumed to be true H 1 is the research hypothesis A random sample (n) is used to “reject H 0” If we conclude 'do not reject H 0', this does not necessarily mean that the null hypothesis is true, it only suggests that there is not sufficient evidence to reject H 0; rejecting the null hypothesis then, suggests that the alternative hypothesis may be true. Equality is always part of H 0 (e. g. “=” , “≥” , “≤”). “≠” “<” and “>” always part of H 1 In actual practice, the status quo is set up as H 0 In problem solving, look for key words and convert them into symbols. Some key words include: “improved, better than, as effective as, different from, has changed, etc. ” Inequality Symbol Part of: Larger (or more) than > H 1 Smaller (or less) < H 1 No more than H 0 At least ≥ H 0 Has increased > H 1 Is there difference? ≠ H 1 Has not changed = H 0 Keywords Has “improved”, “is better than”. “is more effective” See left text H 1

Signs in the Tails of a Test

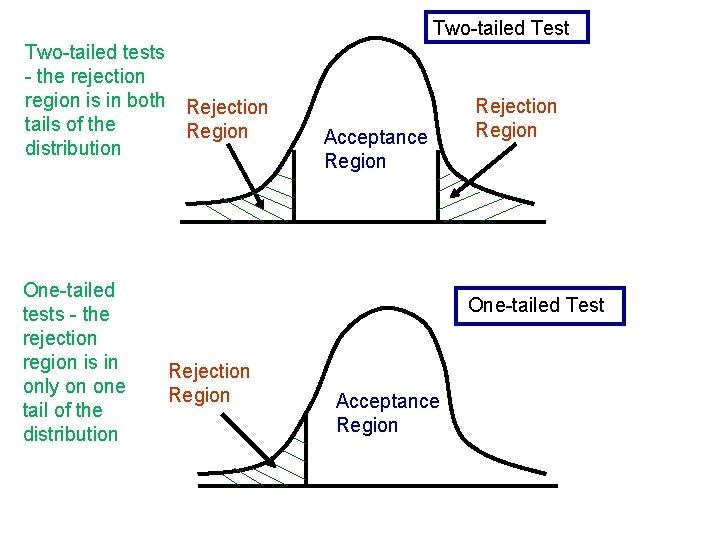
Two-tailed Test Two-tailed tests - the rejection region is in both Rejection tails of the Region distribution One-tailed tests - the rejection region is in only on one tail of the distribution Acceptance Region Rejection Region One-tailed Test Rejection Region Acceptance Region

Types of Errors is true Reject Do not reject is false Type I error P(Type I)= Correct Decision Type II error P(Type II)= Type I Error Defined as the probability of rejecting the null hypothesis when it is actually true. This is denoted by the Greek letter “ ” Also known as the significance level of a test Type II Error: Defined as the probability of “accepting” the null hypothesis when it is actually false. This is denoted by the Greek letter “β”

Hypothesis Setups for Testing a Mean ( ) or a Proportion ( ) MEAN PROPORTION

Steps in hypothesis testing - Define Null hypothesis - Define Alternative hypothesis - Calculate Test statistic - Determine Rejection region - Compare Value of the test statistic with Critical Value - Conclusion

Testing for a Population Mean with a Known Population Standard Deviation- Example EXAMPLE Jamestown Steel Company manufactures and assembles desks and other office equipment. The weekly production of the Model A 325 desk at the Fredonia Plant follows the normal probability distribution with a mean of 200 and a standard deviation of 16. Recently, new production methods have been introduced and new employees hired. The mean number of desks produced during last 50 weeks was 203. 5. The VP of manufacturing would like to investigate whethere has been a change in the weekly production of the Model A 325 desk, at 1% level of significance. Step 1: State the null hypothesis and the alternate hypothesis. H 0: = 200 H 1: ≠ 200 (note: This is a 2 -tail test, as the keyword in the problem “has changed”) Step 2: Select the level of significance. α = 0. 01 as stated in the problem Step 3: Select the test statistic. Use Z-distribution since σ is known Step 4: Formulate the decision rule. Reject H 0 if |Z| > Z /2 Step 5: Make a decision and interpret the result. Because 1. 55 does not fall in the rejection region, H 0 is not rejected. We conclude that the population mean is not different from 200. So we would report to the vice president of manufacturing that the sample evidence does not show that the production rate at the plant has changed from 200 per week.

Testing for a Population Mean with a Known Population Standard Deviation- Another Example Suppose in the previous problem the vice president wants to know whethere has been an increase in the number of units assembled. To put it another way, can we conclude, because of the improved production methods, that the mean number of desks assembled in the last 50 weeks was more than 200? Recall: σ=16, =200, α=. 01 Step 1: State the null hypothesis and the alternate hypothesis. H 0: ≤ 200 H 1: > 200 (note: This is a 1 -tail test as the keyword in the problem “an increase”) Step 2: Select the level of significance. α = 0. 01 as stated in the problem Step 3: Select the test statistic. Use Z-distribution since σ is known Step 4: Formulate the decision rule. Reject H 0 if Z > Z Step 5: Make a decision and interpret the result. Because 1. 55 does not fall in the rejection region, H 0 is not rejected. We conclude that the average number of desks assembled in the last 50 weeks is not more than 200

p-value in Hypothesis Testing n p-VALUE is the probability of observing a sample value as extreme as, or more extreme than, the value observed, given that the null hypothesis is true. n In testing a hypothesis, we can also compare the p-value to the significance level ( ). n Decision rule using the p-value: Reject null hypothesis, if p< α EAMPLE p-Value Recall the last problem where the hypothesis and decision rules were set up as: H 0: ≤ 200 H 1: > 200 Reject H 0 if Z > Z where Z = 1. 55 and Z =2. 33 Reject H 0 if p-value < 0. 0606 is not < 0. 01 Conclude: Fail to reject H 0

Interpreting the p-value n Describing the p-value – If the p-value is less than 1%, there is overwhelming evidence that supports the alternative hypothesis. – If the p-value is between 1% and 5%, there is a strong evidence that supports the alternative hypothesis. – If the p-value is between 5% and 10% there is a weak evidence that supports the alternative hypothesis. – If the p-value exceeds 10%, there is no evidence that supports the alternative hypothesis.

The Power of Statistical Test The power of a statistical test, given as 1 – b = P (reject H 0 when H 0 is false), measures the ability of the test to perform as required. This 1 – b is called the power of the function. This means that greater the power of the function the better would be the decision rule. There are two types of tail test 1. One-tailed tests - the rejection region is in only one tail of the distribution 2. Two-tailed tests - the rejection region is in both tails of the distribution

Steps in Hypothesis Testing using SPSS State the null and alternative hypotheses n Define the level of significance (α) n Calculate the actual significance : p -value n Make decision : Reject null hypothesis, if p≤ α, for 2 -tail test; and if p*≤ α, for 1 -tail test. (p* is p/2 when p is obtained from 2 -tail test) n Conclusion n

Inference About a Population Mean When the Population Standard Deviation Is Unknown or When the Sample Size is Small In practice, the population standard deviation will be unknown. Recall that when s is known we use the following statistic to estimate and test a population mean When s is unknown or when the sample size is small, we use its point estimator s, and the -statistic is replaced then by the t-statistic z

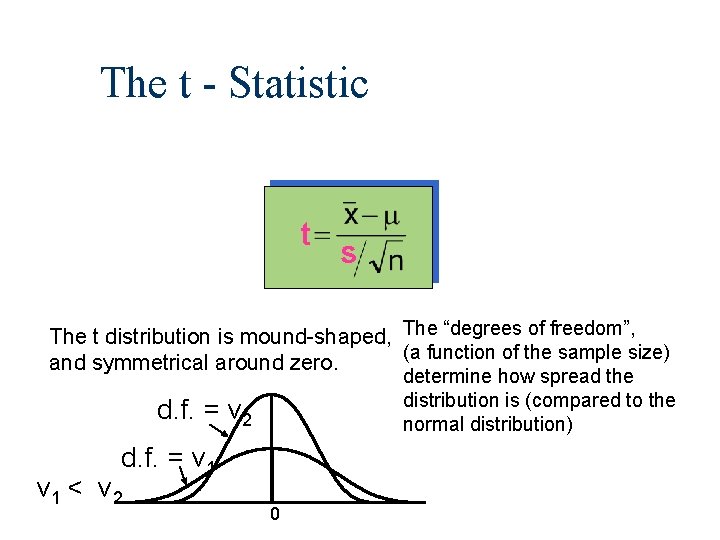
The t - Statistic t s The t distribution is mound-shaped, The “degrees of freedom”, (a function of the sample size) and symmetrical around zero. determine how spread the distribution is (compared to the normal distribution) d. f. = v 2 d. f. = v 1 < v 2 0

Testing when s is unknown n Example – In order to determine the number of workers required to meet demand, the productivity of newly hired trainees is studied. – It is believed that trainees can process and distribute more than 450 packages per hour within one week of hiring. – Can we conclude that this belief is correct, based on productivity observation of 50 trainees (see file PROD. sav).

Testing when s is unknown n Example – Solution – The problem objective is to describe the population of the number of packages processed in one hour. – H 0: = 450 H 1: > 450 – The t statistic d. f. = n - 1 = 49

Testing when s is unknown n Solution continued (solving by hand) – The rejection region is t > t , n – 1 t , n - 1 = t. 05, 49 @ t. 05, 50 = 1. 676.

Testing when s is unknown Rejection region • The test statistic is 1. 676 1. 89 • Since 1. 89 > 1. 676 we reject the null hypothesis in favor of the alternative. • There is sufficient evidence to infer that the mean productivity of trainees one week after being hired is greater than 450 packages at. 05 significance level.

Solution using SPSS (use file PROD. sav) One-Sample Statistics N Packages Mean 50 Std. Deviation 460. 38 Std. Error Mean 38. 827 5. 491 One-Sample Test Value = 450 95% Confidence Interval of the Difference t Packages 1. 890 Sig. (2 tailed) df 49 . 065 Mean Difference 10. 380 Lower -. 65 Upper 21. 41

Inference About a Population Proportion n Statistic and sampling distribution – the statistic used when making inference about p is: – Under certain conditions, [np > 5 and n(1 -p) > 5], is approximately normally distributed, with = p and s 2 = p(1 - p)/n.

Testing and Estimating the Proportion n Test statistic for p

Testing the Proportion n Example 12. 6 – A pharmaceutical company claimed that its medicine was 80% effective in relieving allergy. In a sample of 200 persons, who were given medicine only 150 persons had relief. Do you thank that the effectiveness is below 80%? Use 0. 05 level of significance.

Testing the Proportion n Solution – The problem objective is to test the effectiveness of medicine. – The data are nominal. – The parameter to be tested is ‘p’. – Success is defined as “having relief”. – The hypotheses are: H 0: p =. 8 H 1: p <. 8

Testing the Proportion – Solution • The rejection region is z < z = z. 05 = -1. 645. • The sample proportion is • The value of the test statistic is Since calculated z is less than critical value, we reject null hypothesis and conclude that the claim of the company that its medicine is 80% effective is not justified.

T-Tests : When sample size is small (<30) or When the Population Standard Deviation Is Unknown n n Variable : Normal Types of t-tests: One-sample t-test Paired or dependent sample t-test Independent samples t-test (Equal and Unequal Variance)

One-sample t-test

Paired sample t-test

Matched pairs The mean of the population differences is that is Test statistic: Degree of freedom =

Independent sample t-test

The sampling process. Population 1 Parameters: Statistics: Sample size: Population 2 Parameters: Statistics: Sample size:

If the two population standard deviations are unknown, then we can estimate the standard error of the difference between two means.

Test statistic:

If population variance unknown and the sample size is small and the population variances are equal Then we will use the weighted average called a “ pooled estimate” of Where:

Test statistic: Degree of freedom =

One way Analysis of Variance ( ANOVA ) ANOVA is a technique used to test a hypothesis concerning the means of three or more populations.

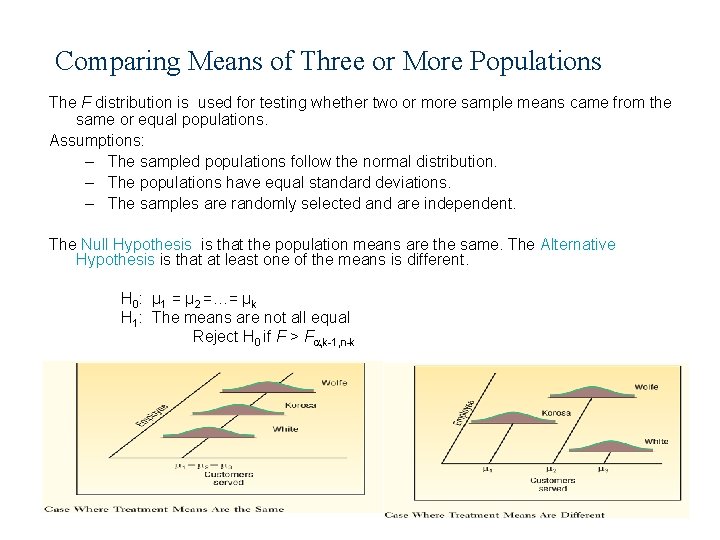
Comparing Means of Three or More Populations The F distribution is used for testing whether two or more sample means came from the same or equal populations. Assumptions: – The sampled populations follow the normal distribution. – The populations have equal standard deviations. – The samples are randomly selected and are independent. The Null Hypothesis is that the population means are the same. The Alternative Hypothesis is that at least one of the means is different. H 0: µ 1 = µ 2 =…= µk H 1: The means are not all equal Reject H 0 if F > F , k-1, n-k

The test statistic used to test the hypothesis is F statistic Assumptions: 1. The random variable is normally distributed. 2. The population variances are equal.

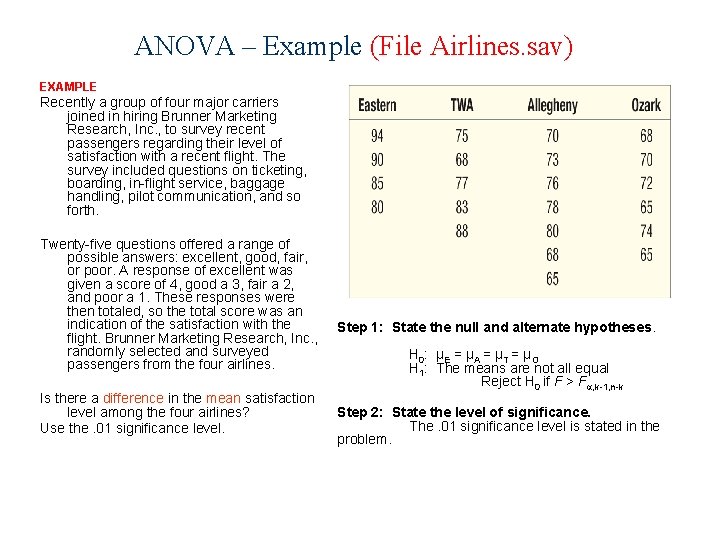
ANOVA – Example (File Airlines. sav) EXAMPLE Recently a group of four major carriers joined in hiring Brunner Marketing Research, Inc. , to survey recent passengers regarding their level of satisfaction with a recent flight. The survey included questions on ticketing, boarding, in-flight service, baggage handling, pilot communication, and so forth. Twenty-five questions offered a range of possible answers: excellent, good, fair, or poor. A response of excellent was given a score of 4, good a 3, fair a 2, and poor a 1. These responses were then totaled, so the total score was an indication of the satisfaction with the flight. Brunner Marketing Research, Inc. , randomly selected and surveyed passengers from the four airlines. Is there a difference in the mean satisfaction level among the four airlines? Use the. 01 significance level. Step 1: State the null and alternate hypotheses. H 0: µE = µA = µT = µO H 1: The means are not all equal Reject H 0 if F > F , k-1, n-k Step 2: State the level of significance. The. 01 significance level is stated in the problem.

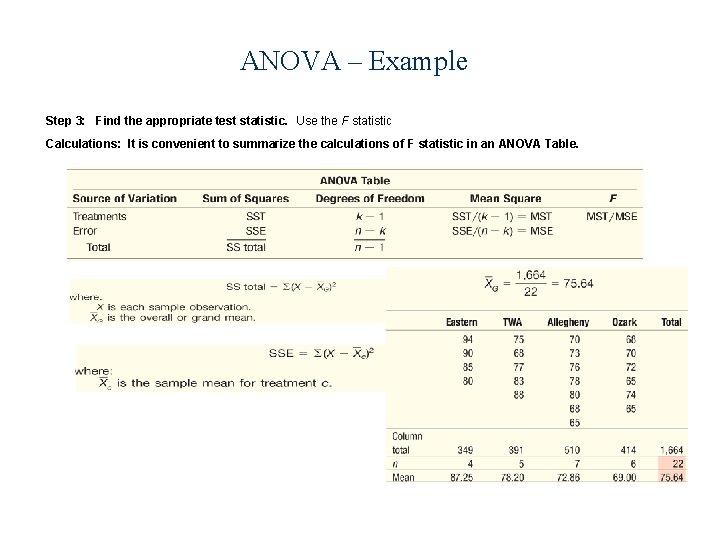
ANOVA – Example Step 3: Find the appropriate test statistic. Use the F statistic Calculations: It is convenient to summarize the calculations of F statistic in an ANOVA Table.

ANOVA – Example Compute the value of F and make a decision We find deviation of each observation from the grand mean, square the deviations, and sum this result for all 22 observations. SS total = {(94 -75. 64)2 + (90 -75. 64)2 + ……+ (6575. 64)2 } = 1485. 10 To compute SSE, find deviation between each observation and its treatment mean. Each of these values is squared and then summed for all 22 observations. SSE = {(94 -87. 25)2 + (90 -87. 25)2 + ……+ (80 -87. 25)2 } + {(75 -78. 20)2 + (68 -78. 20)2 + ……+ (88 -78. 20)2 } + {(70 -72. 86)2 + (73 -72. 86)2 + ……+ (65 -72. 86)2 } + {(68 -69)2 + (7069)2 + ……+ (65 -69)2 } = 594. 41 Finally, determine SST = SS total – SSE. SST = 1485. 10 – 594. 41 = 890. 69

ANOVA – Example Step 3: Find the appropriate test statistic. Use the F statistic Calculations: It is convenient to summarize the calculations of F statistic in an ANOVA Table. Step 4: State the decision rule. Reject H 0 if: F > F , k-1, n-k F > F. 01, 4 -1, 22 -4 F > F. 01, 3, 18 F > 5. 09 Step 5: Make a decision. The computed value of F is 8. 99, which is greater than the critical value of 5. 09, so the null hypothesis is rejected. Conclusion: The mean scores are not the same for the four airlines; at this point we can only conclude there is a difference in the treatment means. We cannot determine which treatment groups differ or how many treatment groups differ.

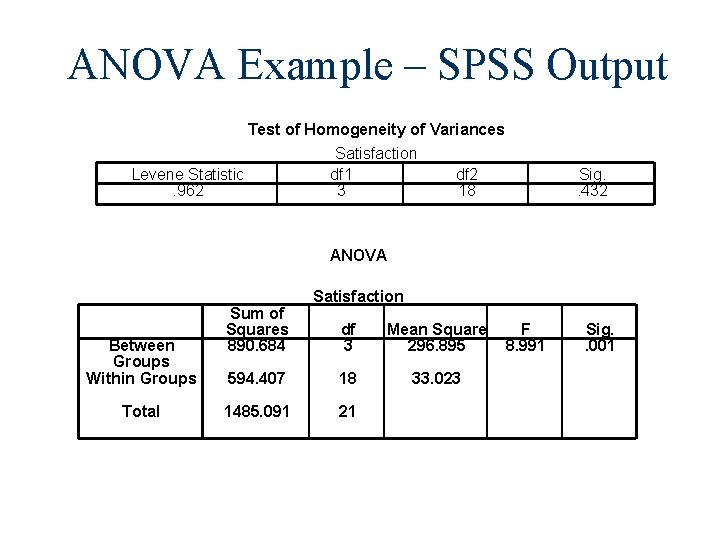
ANOVA Example – SPSS Output Test of Homogeneity of Variances Satisfaction Levene Statistic df 1 df 2. 962 3 18 Sig. . 432 ANOVA Between Groups Within Groups Total Sum of Squares 890. 684 Satisfaction df 3 Mean Square 296. 895 594. 407 18 33. 023 1485. 091 21 F 8. 991 Sig. . 001

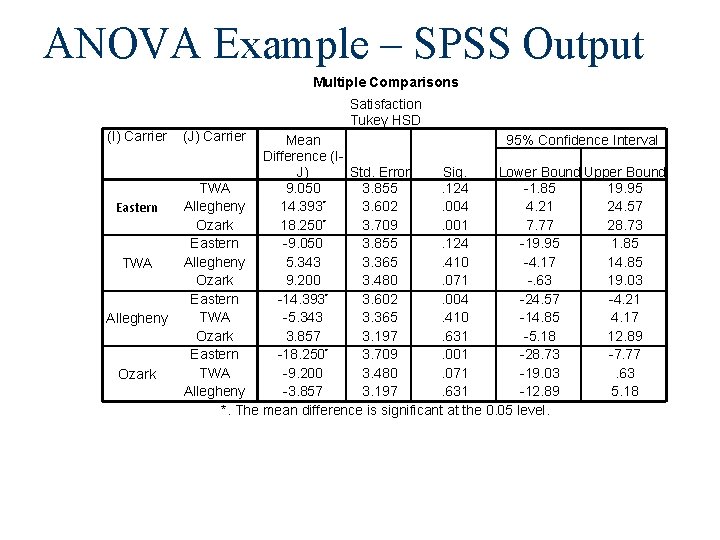
ANOVA Example – SPSS Output Multiple Comparisons Satisfaction Tukey HSD (I) Carrier Eastern TWA Allegheny Ozark (J) Carrier Mean 95% Confidence Interval Difference (IJ) Std. Error Sig. Lower Bound Upper Bound TWA 9. 050 3. 855. 124 -1. 85 19. 95 * Allegheny 14. 393 3. 602. 004 4. 21 24. 57 Ozark 18. 250* 3. 709. 001 7. 77 28. 73 Eastern -9. 050 3. 855. 124 -19. 95 1. 85 Allegheny 5. 343 3. 365. 410 -4. 17 14. 85 Ozark 9. 200 3. 480. 071 -. 63 19. 03 * Eastern -14. 393 3. 602. 004 -24. 57 -4. 21 TWA -5. 343 3. 365. 410 -14. 85 4. 17 Ozark 3. 857 3. 197. 631 -5. 18 12. 89 * Eastern -18. 250 3. 709. 001 -28. 73 -7. 77 TWA -9. 200 3. 480. 071 -19. 03. 63 Allegheny -3. 857 3. 197. 631 -12. 89 5. 18 *. The mean difference is significant at the 0. 05 level.

ANOVA Example – SPSS Output Homogeneous Subsets Satisfaction Tukey HSDa, b Carrier Subset for alpha = 0. 05 Ozark N 6 1 69. 00 Allegheny 7 72. 86 TWA 5 78. 20 Eastern 4 Sig. 2 78. 20 87. 25 . 078 . 085 Means for groups in homogeneous subsets are displayed. a. Uses Harmonic Mean Sample Size = 5. 266. b. The group sizes are unequal. The harmonic mean of the group sizes is used. Type I error levels are not guaranteed.

Chi-squared Test of a Contingency Table n Test of Independence : Test on association between two nominal variables regarding contingency tables. Null Hypothesis : Two variables are independent Alternative Hypothesis : The two variables are dependent

The Chi-square Distribution At the outset, we should know that the chisquare distribution has only one parameter called the ‘degrees of freedom’ (df ) as is the case with the t-distribution. The shape of a particular chi-square distribution depends on the number of degrees of freedom.

Properties of Chi-square Distribution 1. Chi-square is non-negative in value; it is either zero or positively valued. 2. It is not symmetrical; it is skewed to the right. 3. There are many chi-square distributions. As with the t-distribution, there is a different chi-square distribution for each degree-of-freedom value.

The chi-squared statistic measures the difference between the actual counts and the expected counts ( assuming validity of the null hypothesis) The sum ( Observed count - Expected count )2 Expected count

Contingency table c 2 test – Example – In an effort to better predict the demand for courses offered by a certain MBA program, it was hypothesized that students’ academic background affect their choice of MBA major, thus, their courses selection. – A random sample of last year’s MBA students was selected. The data is given in the file Chi-Sq_MBA. sav. – The following contingency table summarizes relevant data.

Contingency table c 2 test – Example The observed values

Contingency table c 2 test – Example n Solution – The hypotheses are: H 0: The two variables are independent H 1: The two variables are dependent – The test statistic k is the number of cells in the contingency table. – The rejection region

Estimating the expected frequencies Undergraduate MBA Major Degree Accounting Finance Marketing BA BENG BBA Other 61 44 47 Probability 61/152 44/152 47/152 60 60 31 39 39 22 Probability 60/152 31/152 39/152 22/152 152 Under the null hypothesis the two variables are independen P(Accounting and BA) = P(Accounting)*P(BA) = [61/152][60/152]. The number of students expected to fall in the cell “Accounting - BA” is e. Acct-BA = n(p. Acct-BA) = 152(61/152)(60/152) = [61*60]/152 = 24. 08 The number of students expected to fall in the cell “Finance - BBA” is e. Finance-BBA = np. Finance-BBA = 152(44/152)(39/152) = [44*39]/152 = 11. 29

The expected frequencies for a contingency table • The expected frequency of cell of raw i and column j in the contingency table is calculated by (Column j total)(Row i total) Eij = Sample size

Calculation of the c 2 statistic • Solution – continued Undergraduate MBA Major Degree Accounting Finance Marketing 31 (24. 08) 24. 0813 (17. 37) 16 (18. 55) BA 31 BENG 8 (12. 44) 16 (8. 97) 7 (9. 58) 24. 08 BBA 31 12 (15. 65) 10 (11. 29) 17 (12. 06) Other 10 (8. 83) 55 (6. 39) (6. 80) 6. 39 77 6. 80 31 24. 08 61 44 47 31 24. 08 31 c 2= 5 6. 39 The expected frequency 5 6. 39 24. 08 7 60 31 39 22 152 6. 80 7 6. 80 5 6. 39 (31 - 24. 08)2 (5 - 6. 39)2 (7 - 6. 80)2 = 14. 70 24. 08 +…. + 6. 39 +…. + 6. 80

Contingency table c 2 test – Example • Solution – continued – The critical value in our example is: • Conclusion: Since c 2 = 14. 70 > 12. 5916, there is sufficient evidence to infer at 5% significance level that students’ undergraduate degree and MBA students courses selection

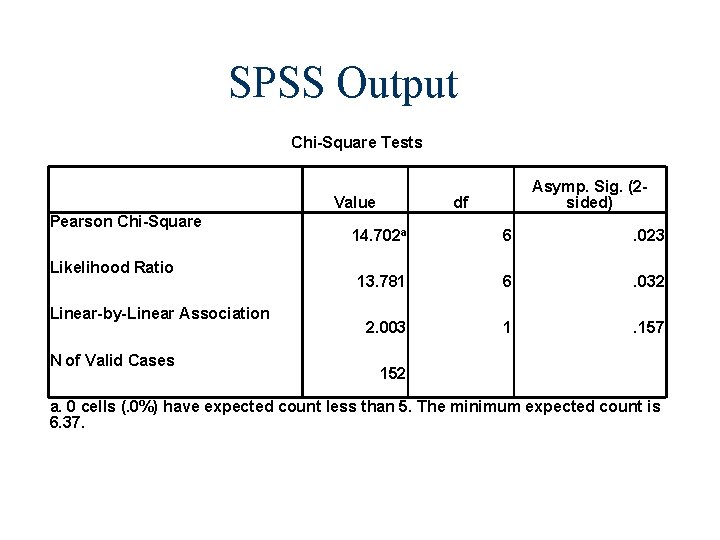
SPSS Output Chi-Square Tests Value Pearson Chi-Square Likelihood Ratio Linear-by-Linear Association N of Valid Cases Asymp. Sig. (2 sided) df 14. 702 a 6 . 023 13. 781 6 . 032 2. 003 1 . 157 152 a. 0 cells (. 0%) have expected count less than 5. The minimum expected count is 6. 37.

Yates’ Correction for Continuity Chi-square distribution is a continuous distribution. Whenever the degrees of freedom (in case of a 2 x 2 table), certain corrections for continuity can be made

Required conditions – the rule of five n n n The test statistic used to perform the test is only approximately Chi-squared distributed. For the approximation to apply, the expected cell frequency has to be at least 5 for all the cells (np ³ 5). If the expected frequency in a cell is less than 5, combine it with other cells.