Chapter 1 Limits and Their Properties Unit Outcomes









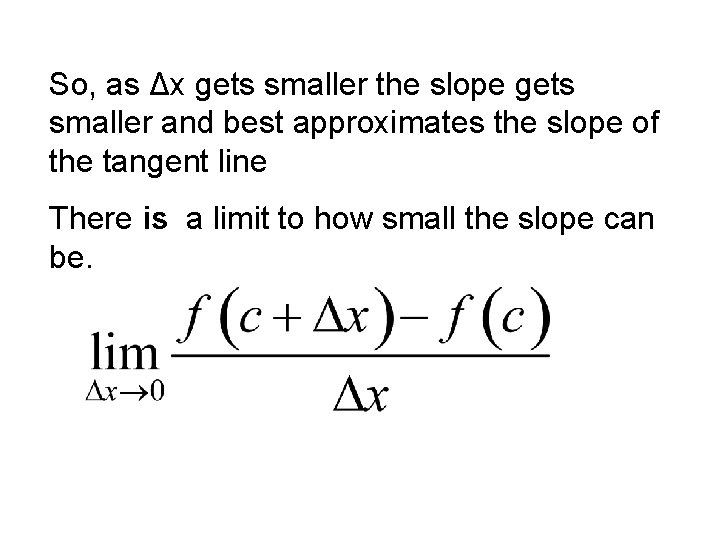










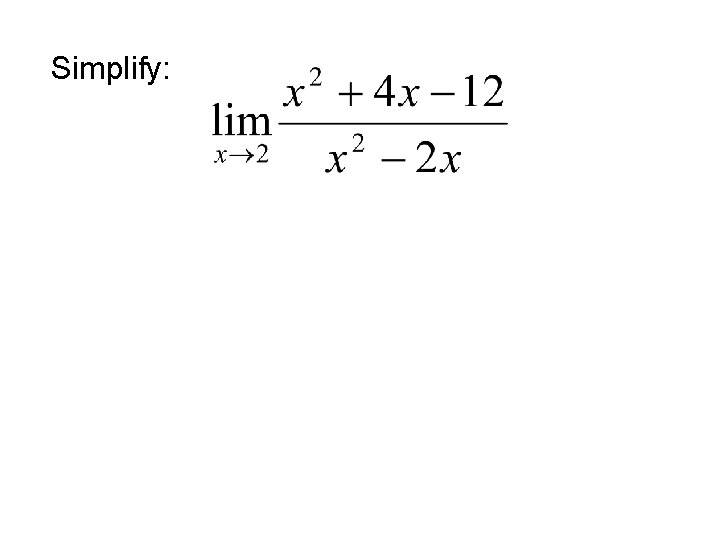











- Slides: 57

Chapter 1 Limits and Their Properties Unit Outcomes – At the end of this unit you will be able to: • Understand what calculus is and how it differs from precalculus • Understand that the tangent line and area problems are basic to calculus • Estimate a limit numerically and graphically • Determine when a limit does not exist

• Learn and use a formal definition of a limit • Use properties of limits to evaluate limits • Develop and use a strategy for finding limits • Evaluate limits by “dividing out” and “rationalizing” • Evaluate a limit using the “Squeeze Theorem” • Determine continuity at a point and continuity on an open interval • Determine one-sided limits and continuity on a closed interval

q. Use properties of continuity q. Know and use the Intermediate Value Theorem q. Determine infinite limits from the left and the right q. Find and sketch the vertical asymptotes of the graph of a function

1. 1 A Preview of Calculus What is Calculus? ? ? ? ?

What Is Calculus • • One answer is to say it is a "limit machine" Involves three stages 1. Precalculus/algebra mathematics process • Building blocks to produce calculus techniques 2. Limit process • The stepping stone to calculus 3. Calculus • Derivatives, integrals

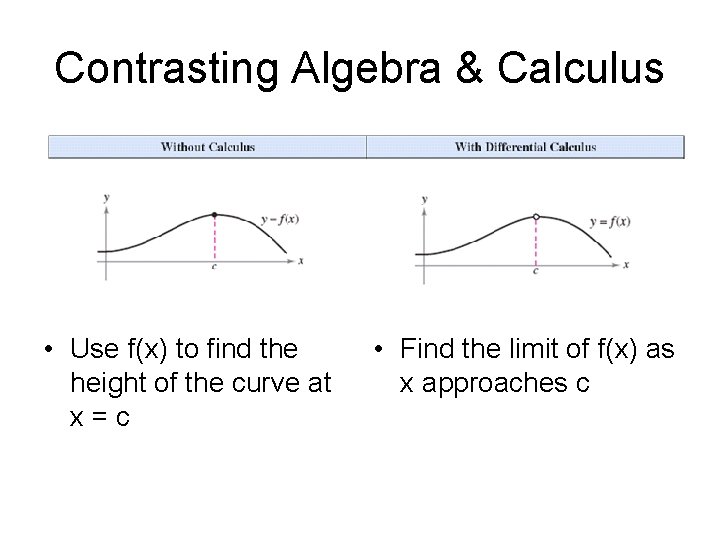
Contrasting Algebra & Calculus • Use f(x) to find the height of the curve at x=c • Find the limit of f(x) as x approaches c

Contrasting Algebra & Calculus • Find the average rate of change between t = a and t = b • Find the instantaneous rate of change at t = c

Contrasting Algebra & Calculus • Area of a rectangle • Area between two curves

A Preview of Calculus (cont’d)

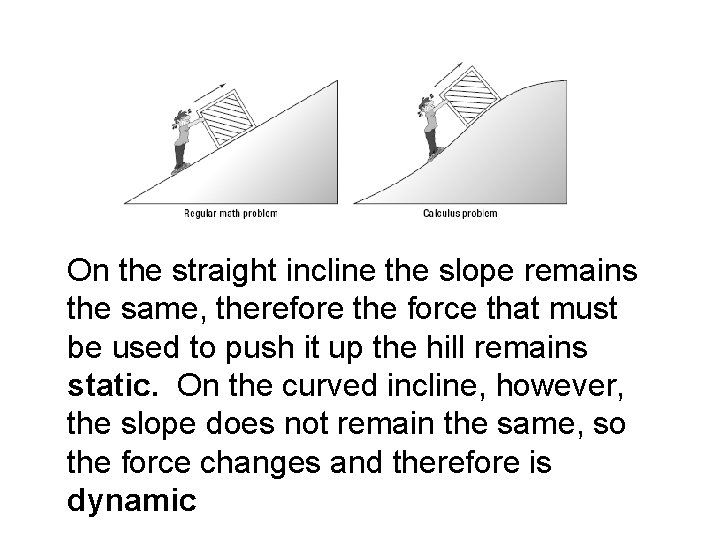
• Calculus is a branch of mathematics that deals with rates of change like velocity and acceleration. What we know of Calculus today, began in the 17 th century with Newton and Leibnitz • Calculus deals primarily with limits, derivatives and integrals • How does Calculus differ from Precalculus? Precalculus is static while Calculus is dynamic See the chart on page 43

On the straight incline the slope remains the same, therefore the force that must be used to push it up the hill remains static. On the curved incline, however, the slope does not remain the same, so the force changes and therefore is dynamic

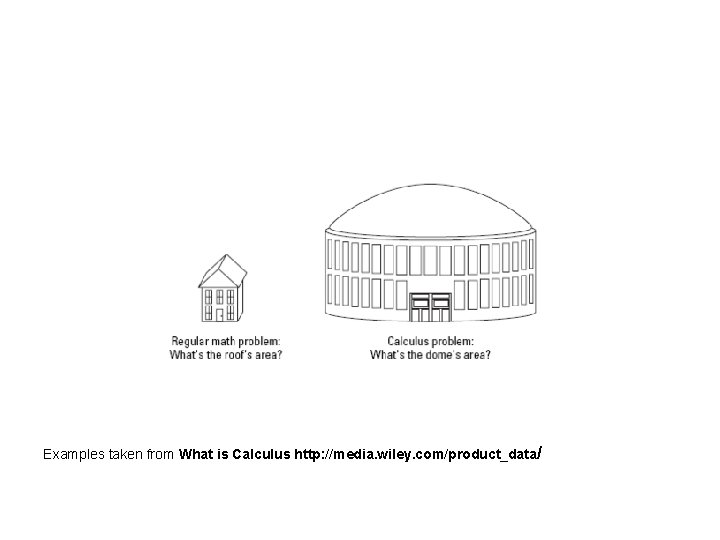
Examples taken from What is Calculus http: //media. wiley. com/product_data/

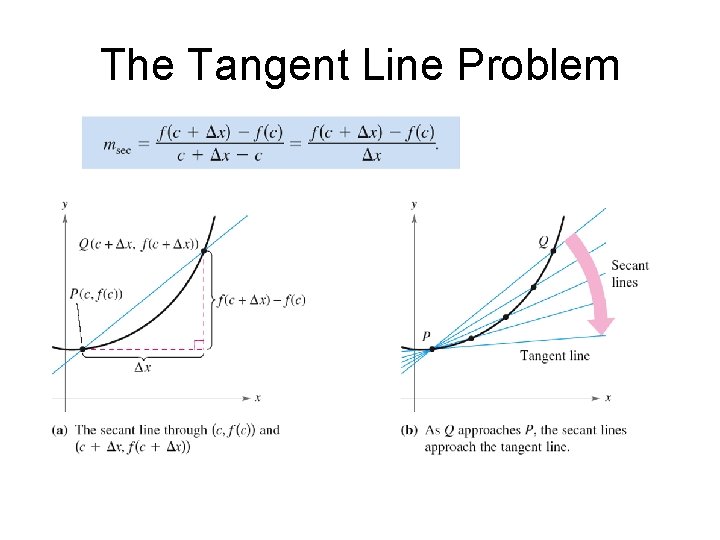
Two problems are basic to the study of calculus: The tangent line problem and the area problem The Tangent Line Problem The graph of a linear equation has a constant slope, but the graph of a quadratic equation does not. So, to find the slope of the curve at a certain point, we find the slope of the tangent line at that point

TANGENT LINE

How will we determine the slope of the tangent line?

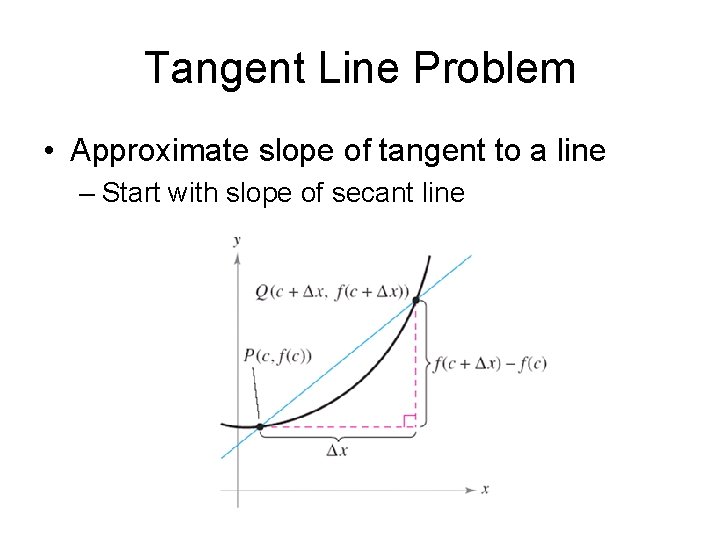
Tangent Line Problem • Approximate slope of tangent to a line – Start with slope of secant line

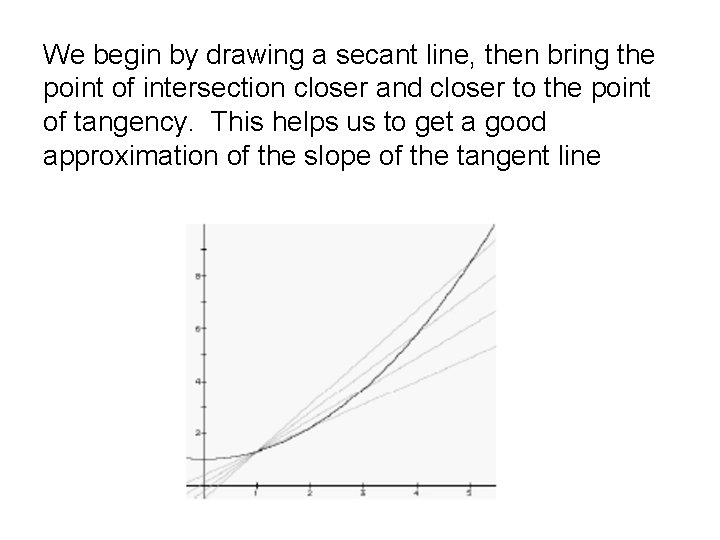
We begin by drawing a secant line, then bring the point of intersection closer and closer to the point of tangency. This helps us to get a good approximation of the slope of the tangent line

The Tangent Line Problem
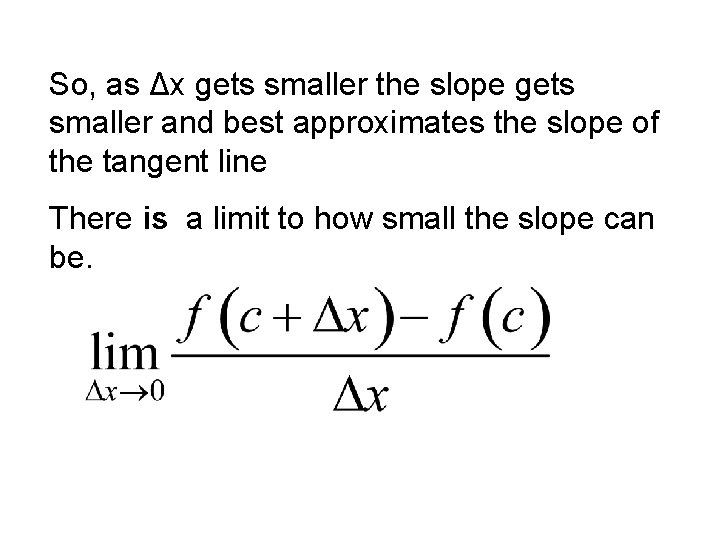
So, as Δx gets smaller the slope gets smaller and best approximates the slope of the tangent line There is a limit to how small the slope can be.

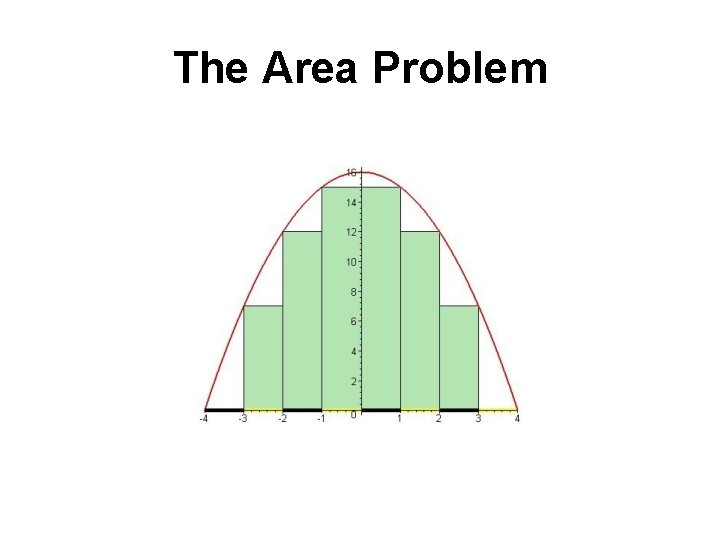
The Area Problem


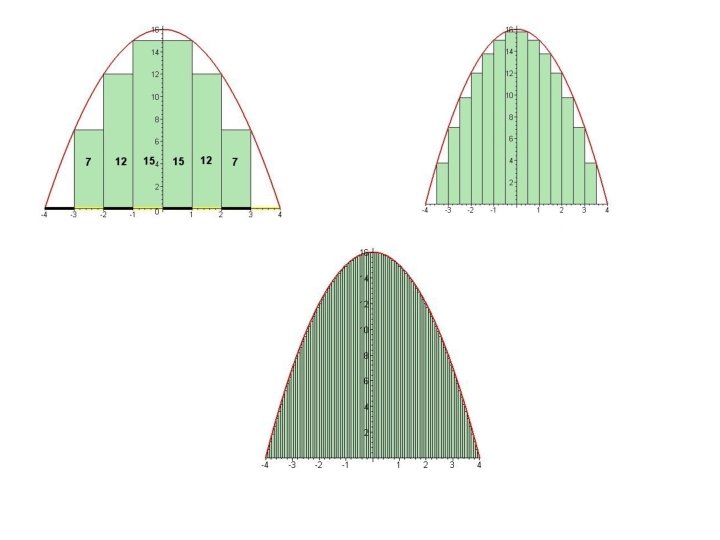
• In other words!!!! As we increase the number of rectangles, we get closer and closer to the actual area of under the curve!! • Or we could say “as the limit of the number of rectangles approaches infinity”!!!! “we get closer and closer to the actual area under the curve!!!!

Ways to Evaluate Limits: • Graphically – show graph and arrows traveling from each side of the x-value to find limit • Numerically – show table values from both the right and left of the xvalue to discover limit • Analytically - algebraically

In AP Calculus, we will be approaching problems in three different ways: q. Analytically (using the equation) q. Numerically q. Graphically

Finding Limits Graphically and Numerically

Finding Limits Graphically The informal definition of a limit is “what is happening to y as x gets close to a certain number”

Notation for a Limit This is read: The limit of f of x as x approaches c equals L.

If we are concerned with the limit of f(x) as we approach some value c from the left hand side, we write

One-sided Limits—Left-Hand Limit This is read--The limit of f as x approaches c from the left.

If we are concerned with the limit of f(x) as we approach some value c from the right hand side, we write

One-sided Limits—Right-Hand Limit This is read: The limit of f as x approaches c from the right.

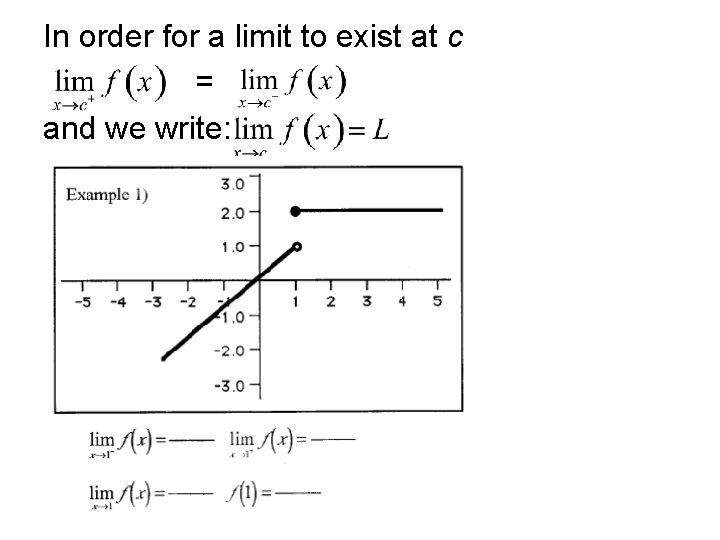
Definition of a Limit If the righthand lefthand limits are equal and exist, then the limit exists.

In order for a limit to exist at c = and we write:

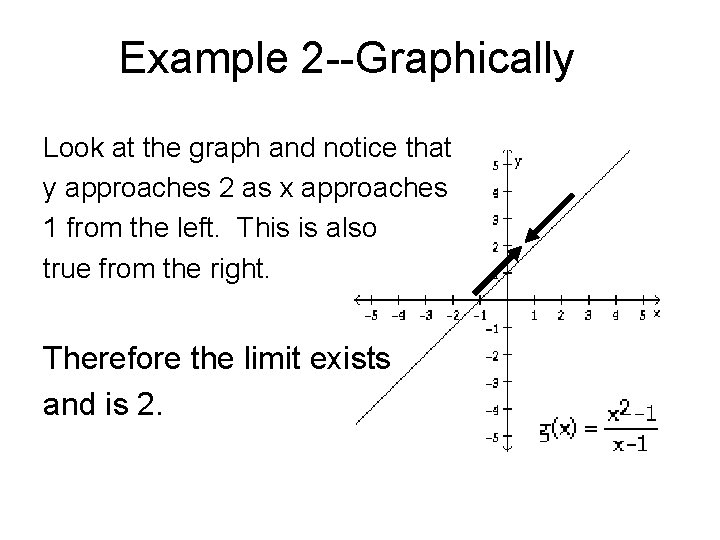
Example 2 --Graphically Look at the graph and notice that y approaches 2 as x approaches 1 from the left. This is also true from the right. Therefore the limit exists and is 2.

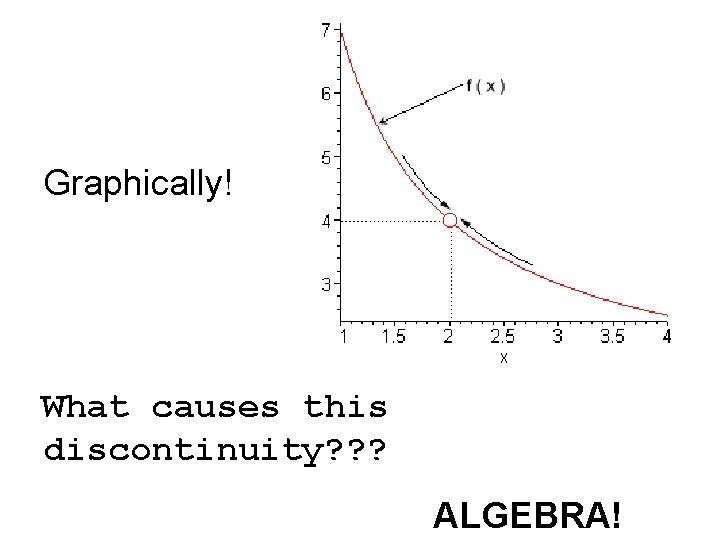
Graphically! What causes this discontinuity? ? ? ALGEBRA!
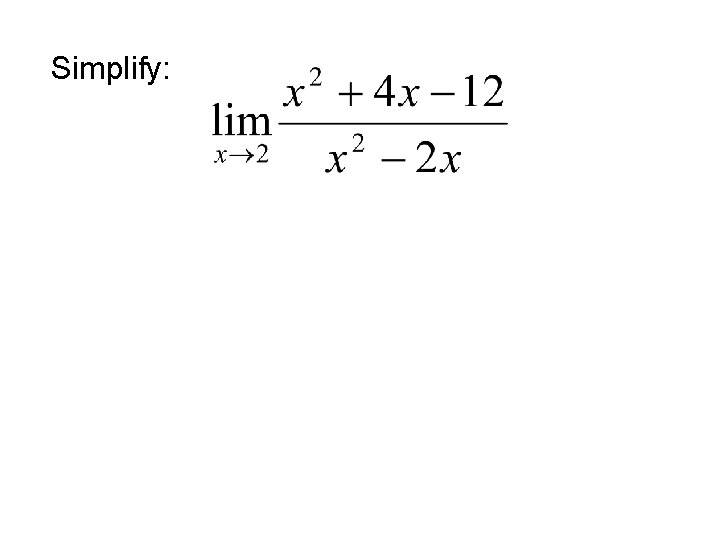
Simplify:

When we are computing limits the question that we are really asking is what y value is our graph “intending to take” as we move on towards x = 2 on our graph. We are NOT asking what y value the graph takes at the point in question!

Example 2 --Numerically Look at the table and notice that y approaches 2 as x approaches 1 from the left. (slightly smaller than 1) This is also true from the right. (slightly larger than 1) Therefore the limit Exists and is 2.

Finding Limits Determine whether the limit exists. If it does, compute it. EXAMPLE SOLUTION Let us make a table of values of x approaching 4 and the corresponding values of x 3 – 7 as we approach for both from above (from the right) and below (from the left) x x 3 - 7 4. 1 61. 921 3. 9 52. 319 4. 01 57. 481 3. 99 56. 521 4. 001 57. 048 3. 999 56. 952 4. 0001 57. 005 3. 9999 56. 995 As x approaches 4, it appears that x 3 – 7 approaches 57. In terms of our notation,

One more try…. . • • • Turn on the TI-83/84 or 89 Graph y = 2 x + 2 Create a table Study what happens as x approaches 5. Make sure your tblset is set to: Independent “ask”. You can then choose any x value you like and get its y-value

From the Left x f(x) From the Right x f(x)

Example. Evaluate the following limit:

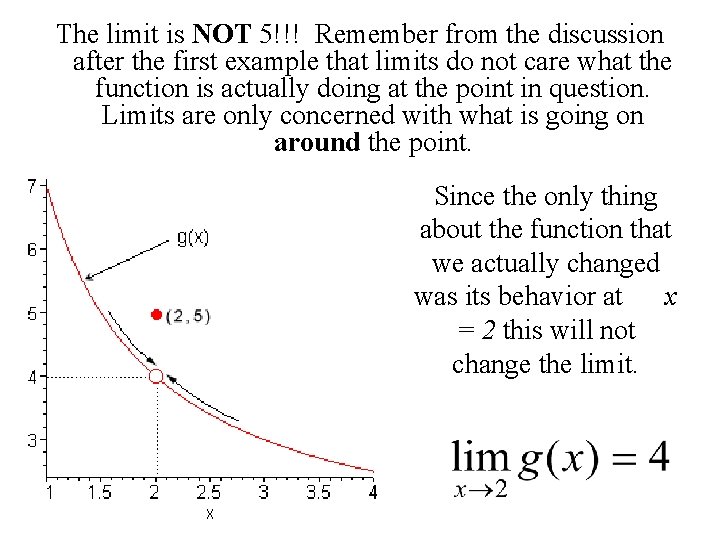
The limit is NOT 5!!! Remember from the discussion after the first example that limits do not care what the function is actually doing at the point in question. Limits are only concerned with what is going on around the point. Since the only thing about the function that we actually changed was its behavior at x = 2 this will not change the limit.

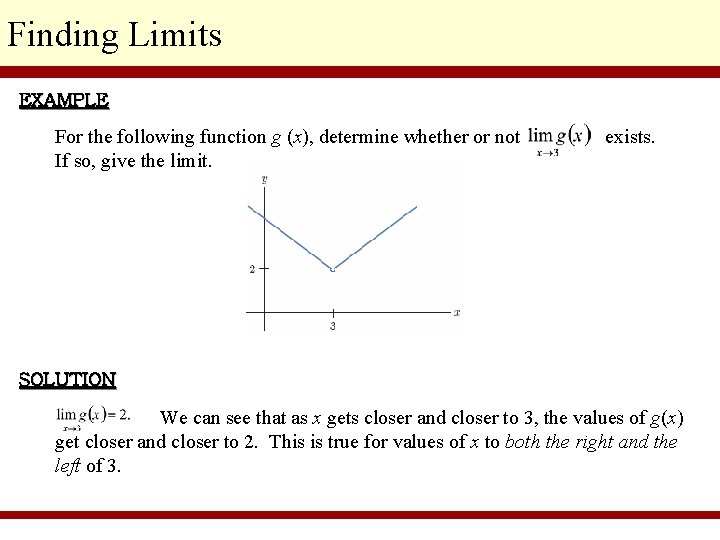
Finding Limits EXAMPLE For the following function g (x), determine whether or not If so, give the limit. exists. SOLUTION We can see that as x gets closer and closer to 3, the values of g(x) get closer and closer to 2. This is true for values of x to both the right and the left of 3.

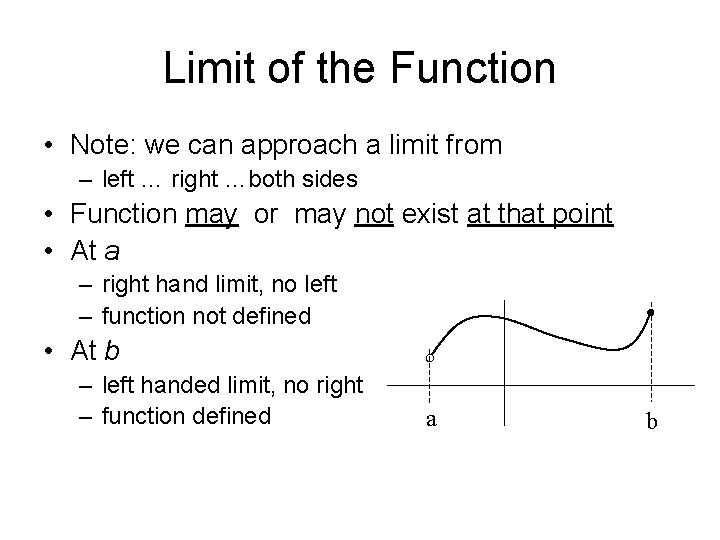
Limit of the Function • Note: we can approach a limit from – left … right …both sides • Function may or may not exist at that point • At a – right hand limit, no left – function not defined • At b – left handed limit, no right – function defined a b

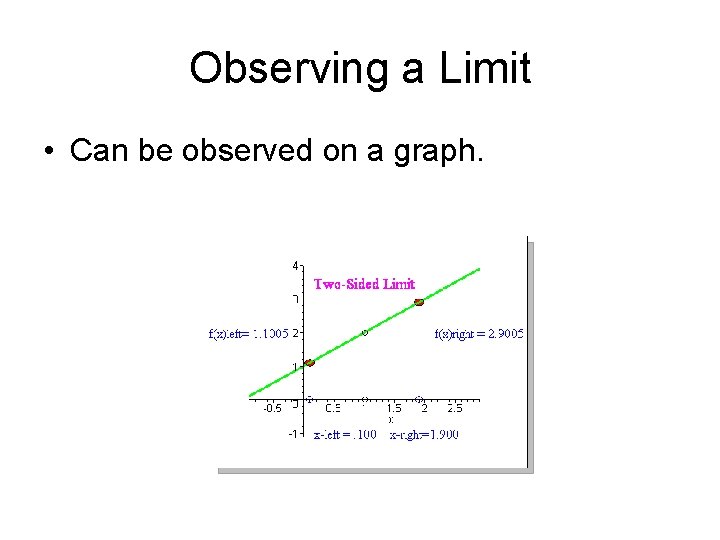
Observing a Limit • Can be observed on a graph.

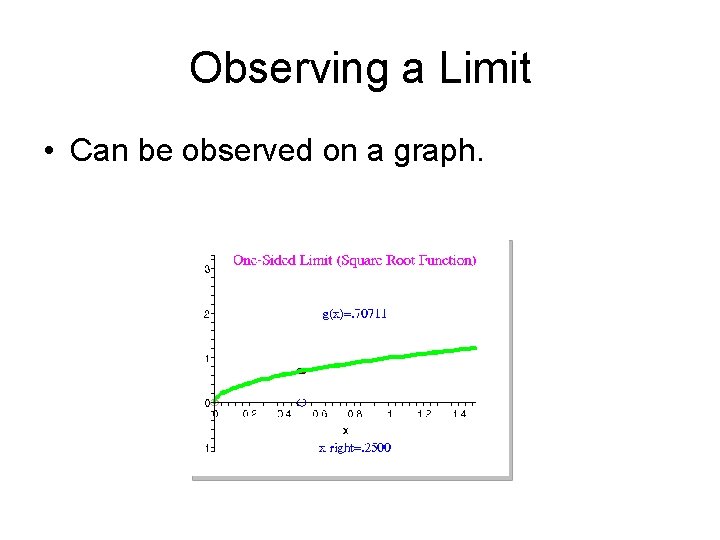
Observing a Limit • Can be observed on a graph.

Find each limit, if it exists. In order for a limit to exist, the two sides of a graph must match at the given x-value. D. S.

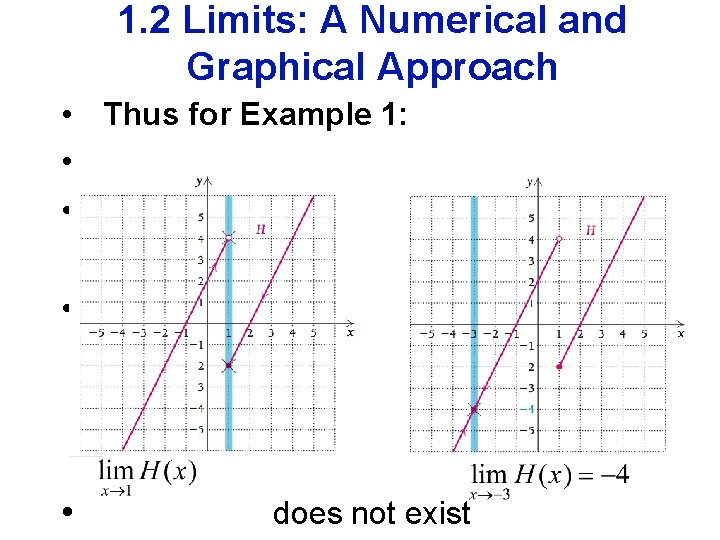
1. 2 Limits: A Numerical and Graphical Approach • Thus for Example 1: • • does not exist

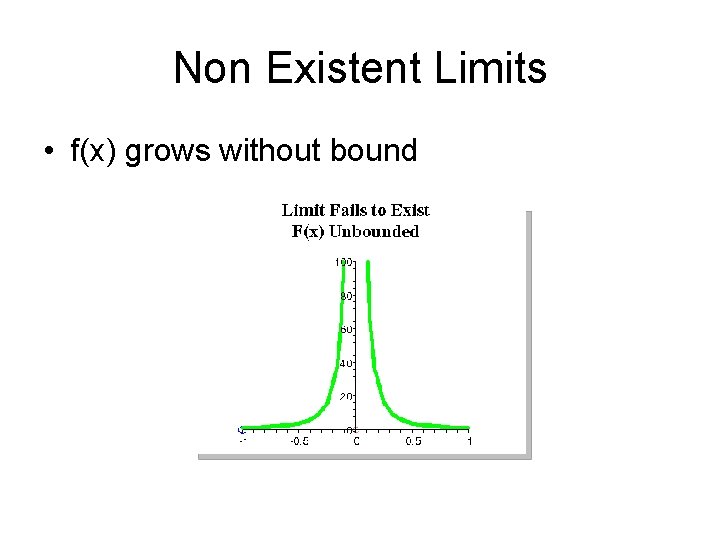
Non Existent Limits • f(x) grows without bound

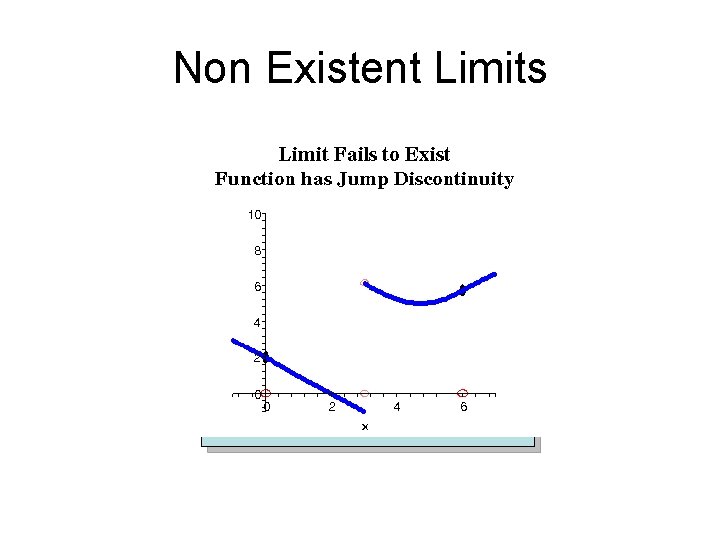
Non Existent Limits

Graphical Example 2 What happens as x approaches zero? The limit as x approaches zero does not exist.

Graphical Example 2 What happens as x approaches zero? The limit as x approaches zero does not exist.

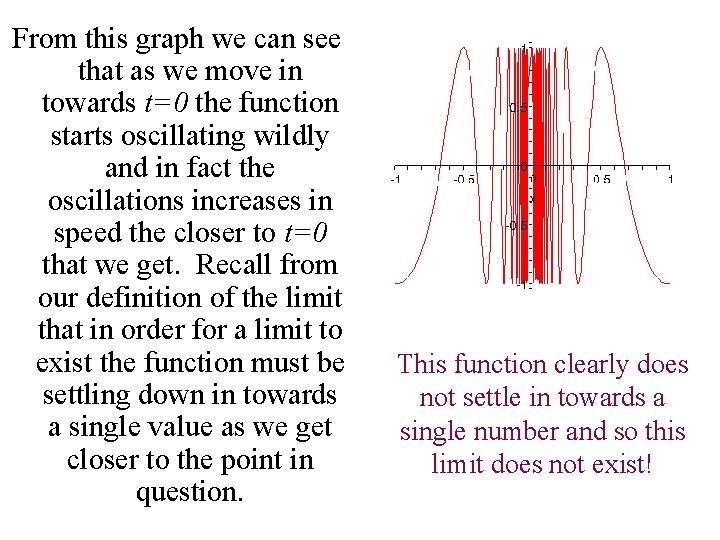
From this graph we can see that as we move in towards t=0 the function starts oscillating wildly and in fact the oscillations increases in speed the closer to t=0 that we get. Recall from our definition of the limit that in order for a limit to exist the function must be settling down in towards a single value as we get closer to the point in question. This function clearly does not settle in towards a single number and so this limit does not exist!

Common Types of Behavior Associated with Nonexistence of a Limit

SUMMATION • Introduction to limits – The limit of a function is the y value the graph is getting closer to as x gets closer to a particular value – Making a table of values to calculate the limit – must be done on a calculator – Sketch a graph to calculate the limit, or use an already existing graph to calculate the limit

When limits fail to exist 1. When the right hand left hand limits do not agree 2. When there is unbounded behavior (as we have just seen) 3. When there is oscillating behavior