Anisotropic Voronoi Diagrams and GuaranteedQuality Anisotropic Mesh Generation

Anisotropic Voronoi Diagrams and Guaranteed-Quality Anisotropic Mesh Generation François Labelle Jonathan Richard Shewchuk Computer Science Division University of California at Berkeley, California Presented by Jessica Schoen

Outline Anisotropic meshes Anisotropic Voronoi diagrams Algorithm for anisotropic mesh generation Current research

I. Anisotropic Meshes

What Are Anisotropic Meshes? Meshes with long, skinny triangles (in the right places). Why are they important? • Often provide better interpolation of multivariate functions with fewer triangles. • Used in finite element methods to resolve boundary layers and shocks. Source: “Grid Generation by the Delaunay Triangulation, ” Nigel P. Weatherill, 1994.

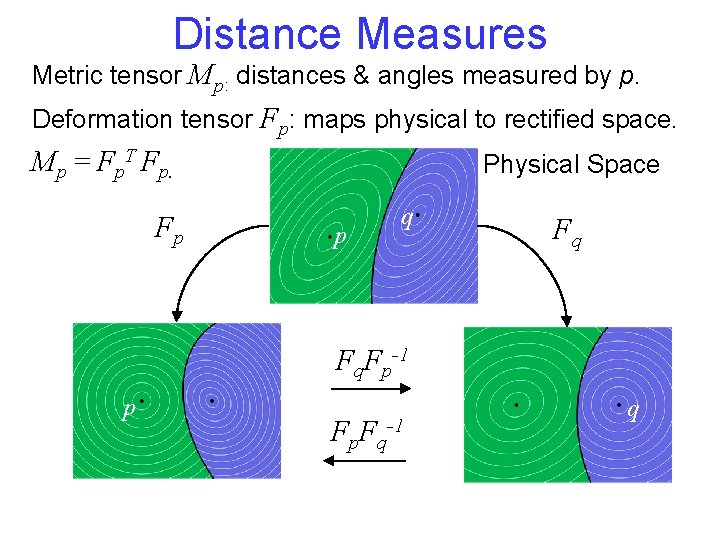
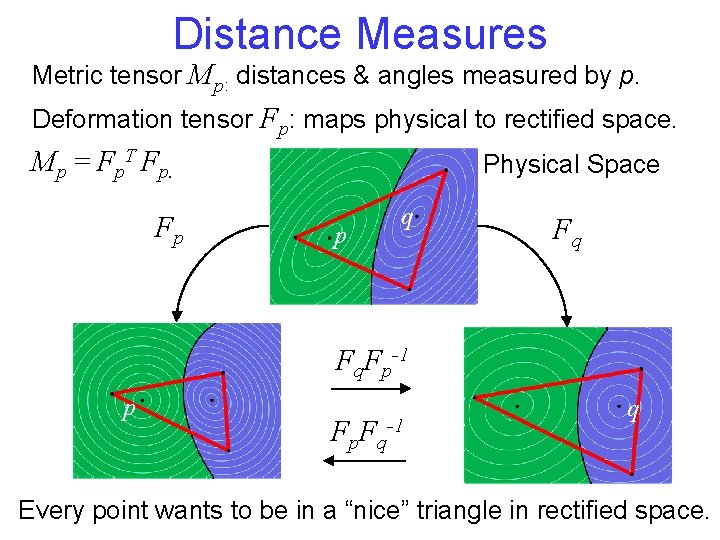
Distance Measures Metric tensor Mp: distances & angles measured by p. Deformation tensor Fp: maps physical to rectified space. Mp = Fp. T Fp. Fp Physical Space p q Fq Fq. Fp-1 p Fp. Fq-1 q

Distance Measures Metric tensor Mp: distances & angles measured by p. Deformation tensor Fp: maps physical to rectified space. Mp = Fp. T Fp. Fp Physical Space p q Fq Fq. Fp-1 p Fp. Fq-1 q Every point wants to be in a “nice” triangle in rectified space.

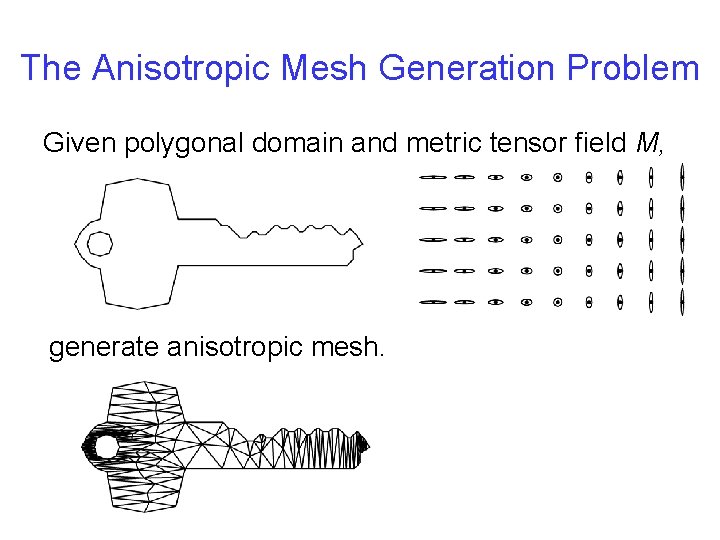
The Anisotropic Mesh Generation Problem Given polygonal domain and metric tensor field M, generate anisotropic mesh.

A Hard Problem (Especially in Theory) Common approaches to guaranteed-quality mesh generation do not adapt well to anisotropy. • Quadtree-based methods can be adapted to horizontal and vertical stretching, but not to diagonal stretching. • Delaunay triangulations lose their global optimality properties when adapted to anisotropy. No “empty circumellipse” property.

Heuristic Algorithms for Generating Anisotropic Meshes George-Borouchaki [1998] Bossen-Heckbert [1996] Shimada-Yamada-Itoh [1997] Li-Teng-Üngör [1999]

II. Anisotropic Voronoi Diagrams

Voronoi Diagram: Definition Given a set V of sites in Ed, decompose Ed into cells. The cell Vor(v) is the set of points “closer” to v than to any other site in V. Mathematically: Vor(v) = {p in Ed: dv(p)≤ dw(p) for every w in V. } distance from v to p as measured by v

Distance Function Examples 1. Standard Voronoi diagram dv(p) = || p – v ||2

Distance Function Examples 2. Multiplicatively weighted Voronoi diagram dv(p) = cv|| p – v ||2

Distance Function Examples 3. Anisotropic Voronoi diagram dv(p) = [(p – v)TMv(p – v)]1/2

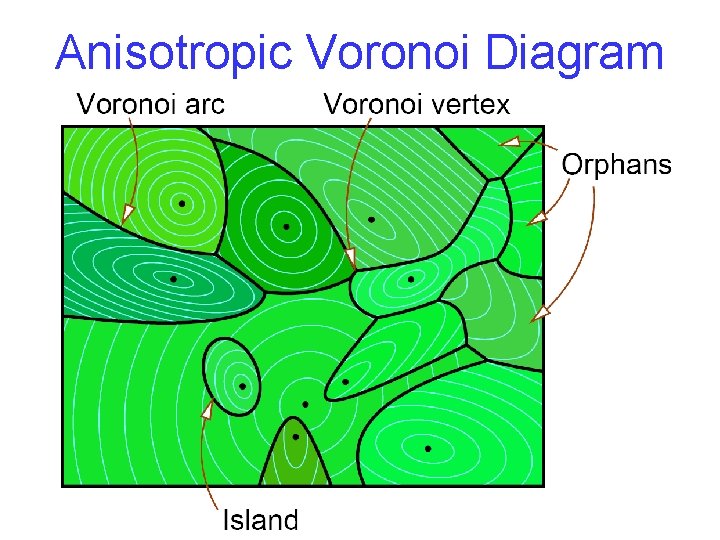
Anisotropic Voronoi Diagram

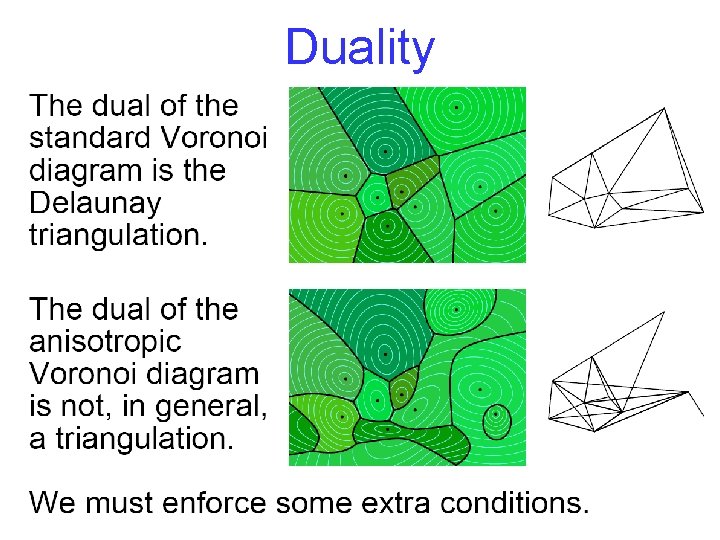
Duality

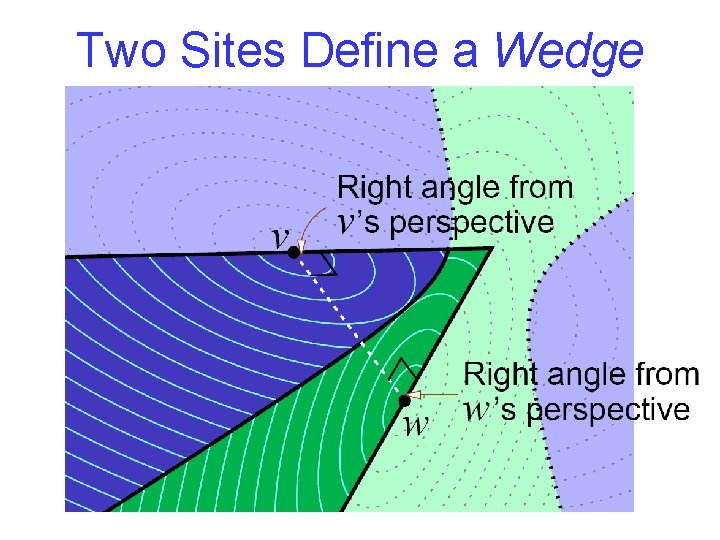
Two Sites Define a Wedge

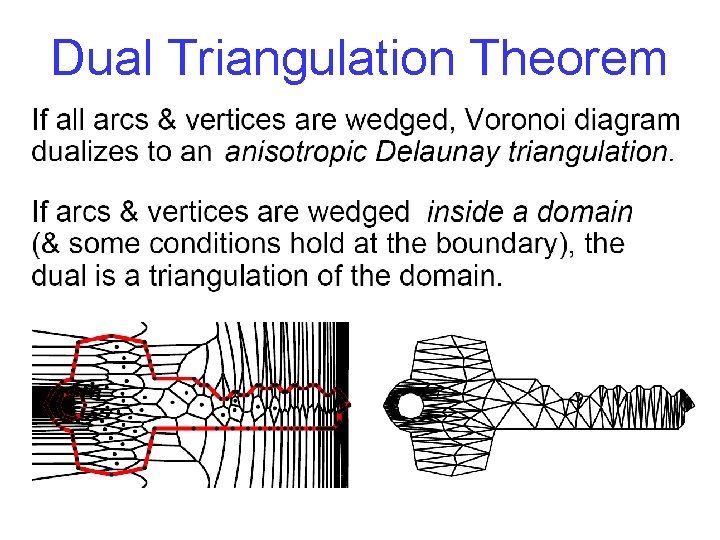
Dual Triangulation Theorem

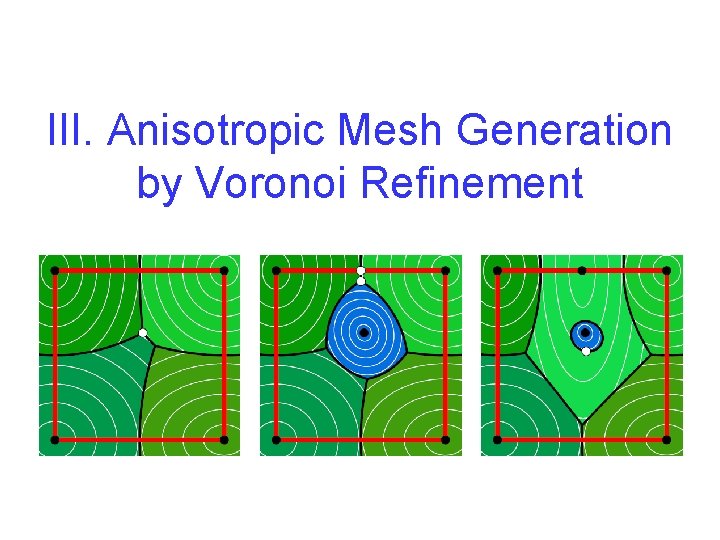
III. Anisotropic Mesh Generation by Voronoi Refinement

Easy Case: M = constant

Easy Case: M = constant

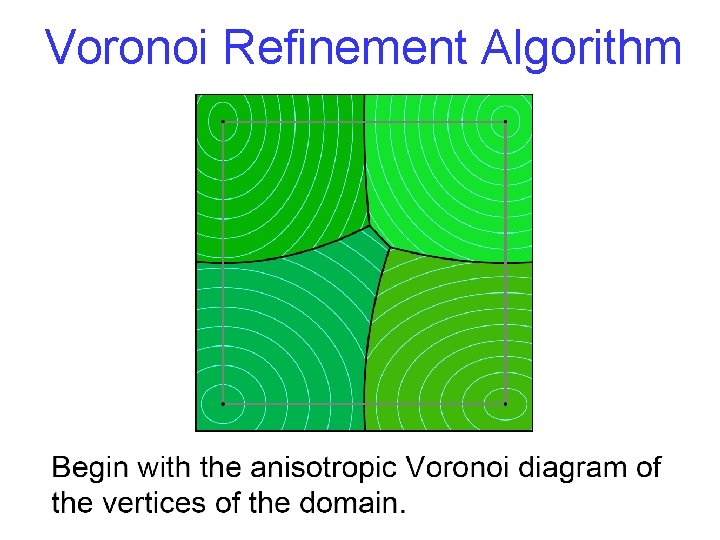
Voronoi Refinement Algorithm

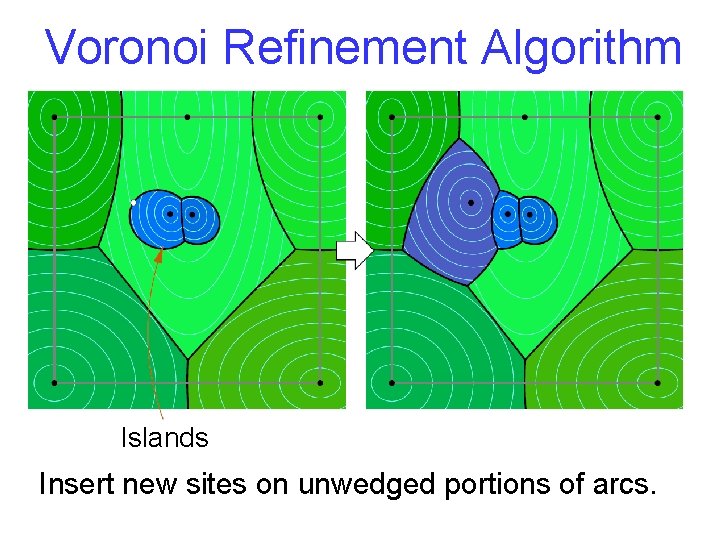
Voronoi Refinement Algorithm Islands Insert new sites on unwedged portions of arcs.

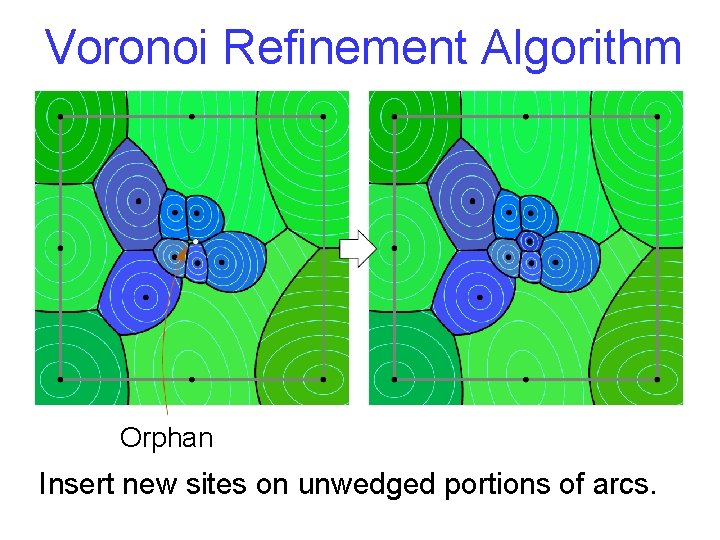
Voronoi Refinement Algorithm Orphan Insert new sites on unwedged portions of arcs.

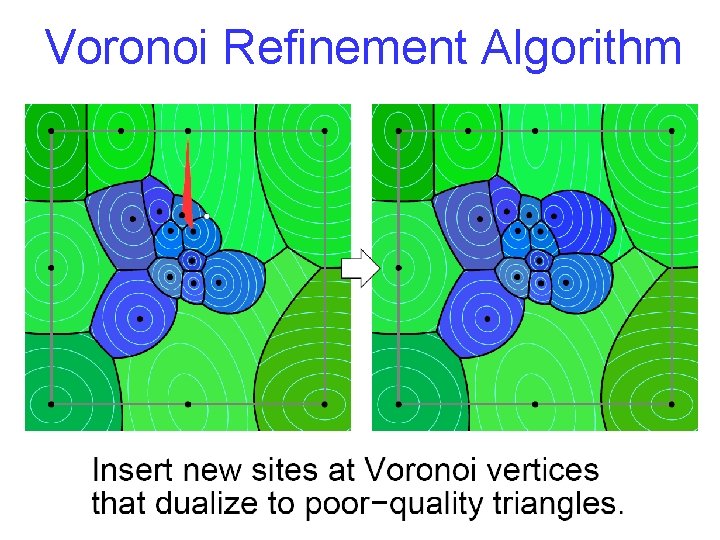
Voronoi Refinement Algorithm

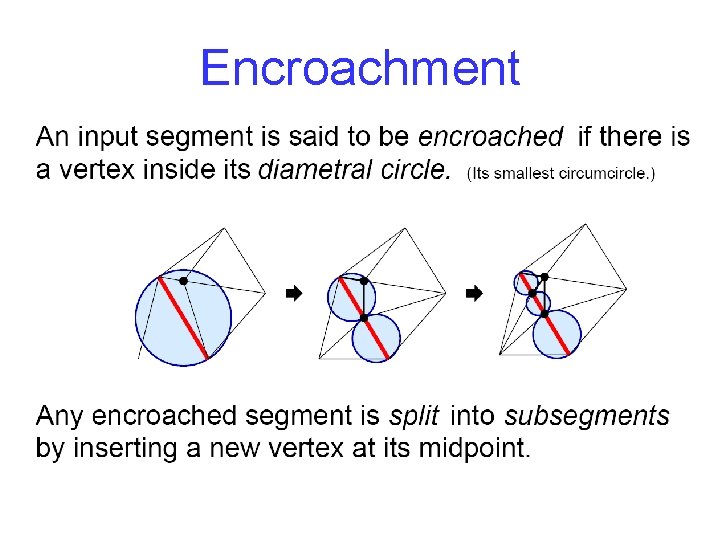
Encroachment

Special Rules for the Boundary

Special Rules for the Boundary

Main Result

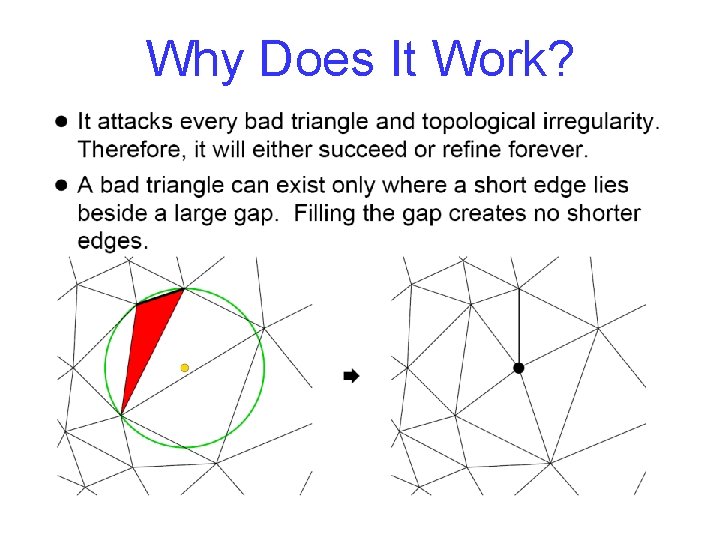
Why Does It Work?

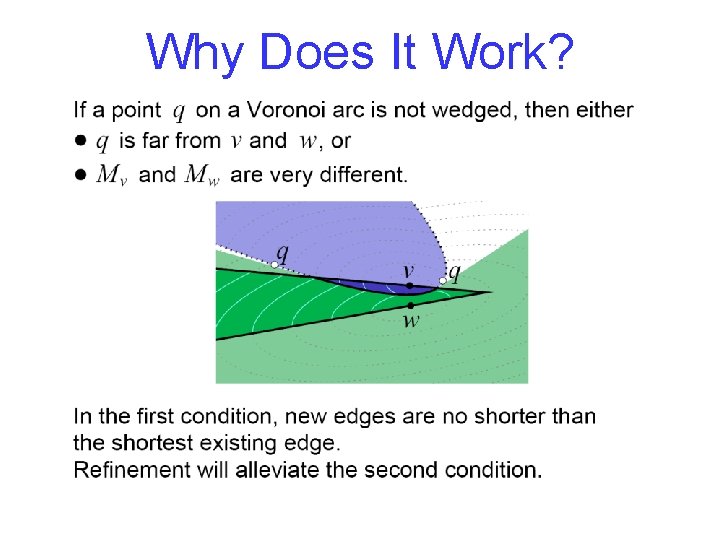
Why Does It Work?

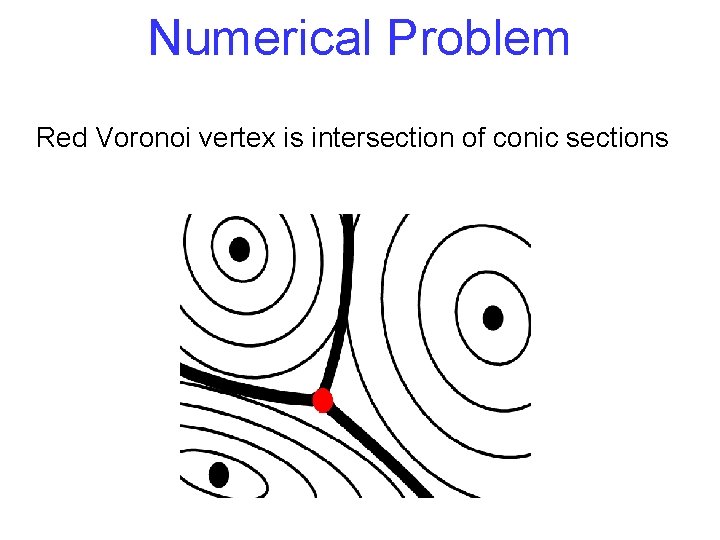
Numerical Problem Red Voronoi vertex is intersection of conic sections

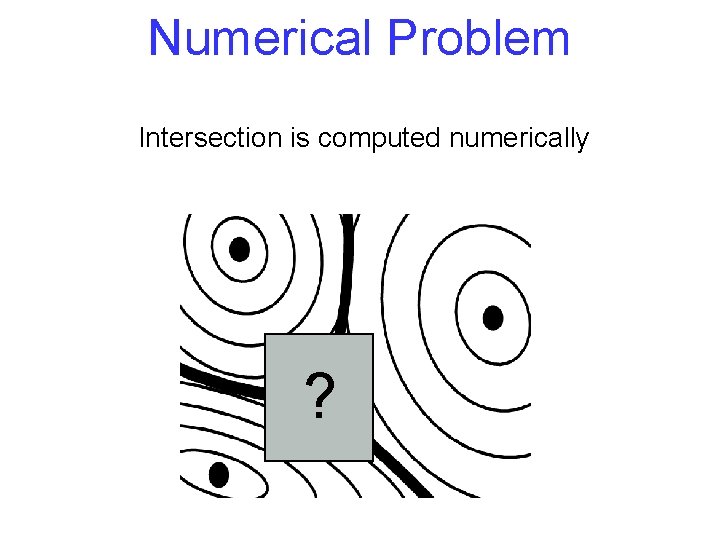
Numerical Problem Intersection is computed numerically ?

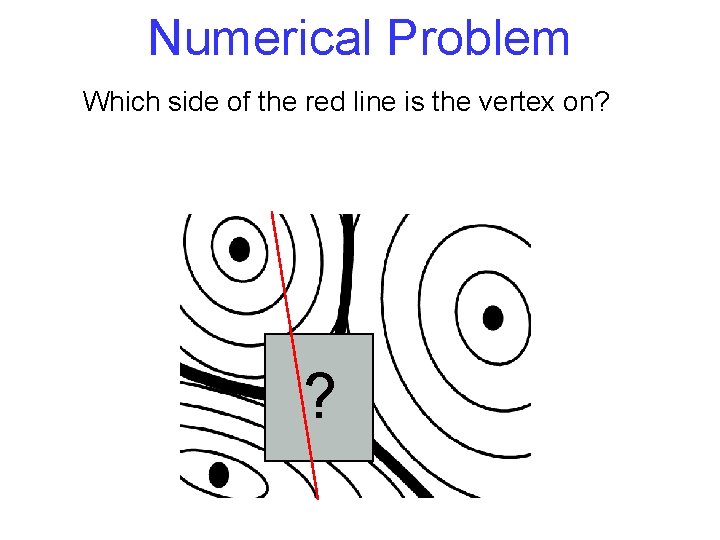
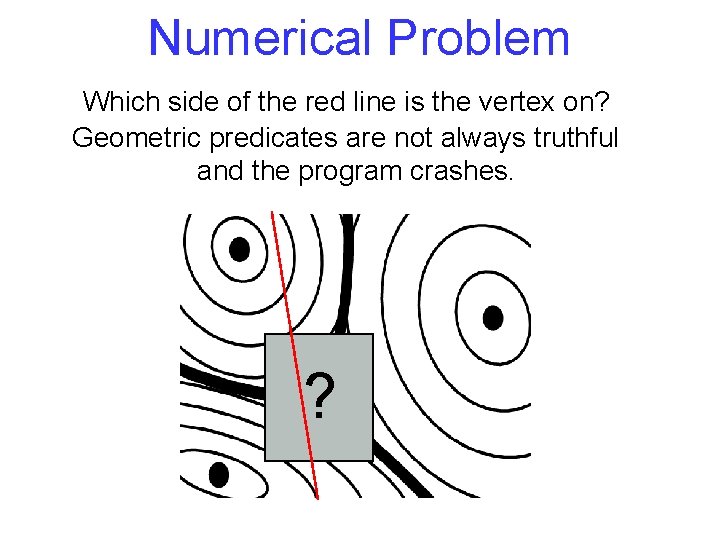
Numerical Problem Which side of the red line is the vertex on? ?

Numerical Problem Which side of the red line is the vertex on? Geometric predicates are not always truthful and the program crashes. ?

IV. My Current Research

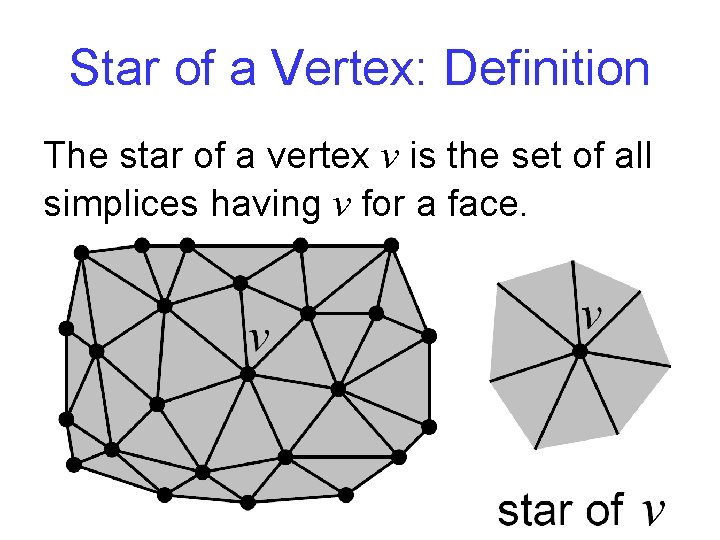
Star of a Vertex: Definition The star of a vertex v is the set of all simplices having v for a face.

Star Based Anisotropic Meshing Each vertex computes its own star independently

Inconsistent Stars If the arcs and vertices of the corresponding anisotropic Voronoi diagram are not all wedged, the diagram may not dualize to a triangulation, and the independently constructed stars may not form a consistent triangulation.

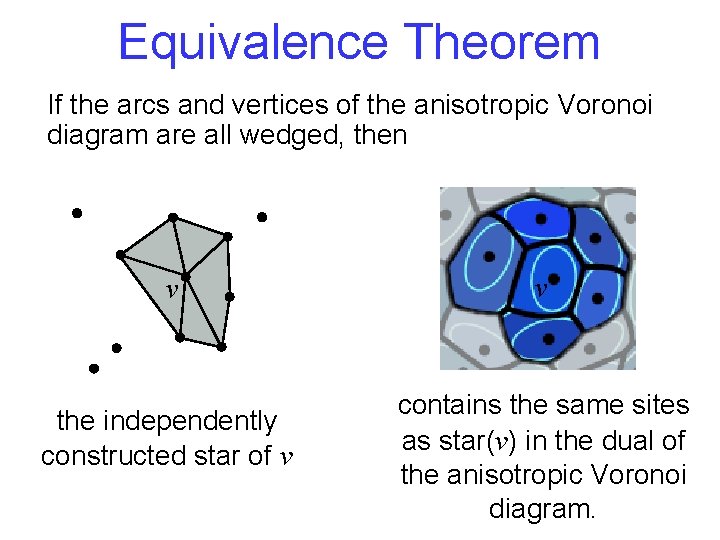
Equivalence Theorem If the arcs and vertices of the anisotropic Voronoi diagram are all wedged, then v the independently constructed star of v v contains the same sites as star(v) in the dual of the anisotropic Voronoi diagram.