UNSTRUCTURED MESH GENERATION Issues in Unstructured Mesh Generation

UNSTRUCTURED MESH GENERATION Issues in Unstructured Mesh Generation by Gopal Shevare ppts are based on Lecture notes by T J Barth (1994)

UNSTRUCTURED MESH GENERATION CONTENTS • Un-structured Grid • Unstructured Grids and Application of Graph Theory • Delaunay Triangulation and Voronoi diagrams • Methods of Delaunay Triangulations • Method of Non- Triangulation

UNSTRUCTURED MESH GENERATION Grid Generation Present Status Grid Generation is the gateway for CAE. Grids connects various simulations for designing a products Make grid generation easy and user friendly. If possible make it redundant Grid generation now encompasses each and everything from creating / importing geometry to export a single file that any solver may need irrespective what simulation code is simulating (Boundary Fitted Coordinate) BFC system is not grid generation! Grid generation has become interdisciplinary area where in CAGD, Computational Geometry, CFD, Computer Graphics experts contribute to make a package User may require execution of around 60 to 100 tasks before grid gets ready Present day simulations use millions of grid points Grids are a commodity. There is an ISO format for grids

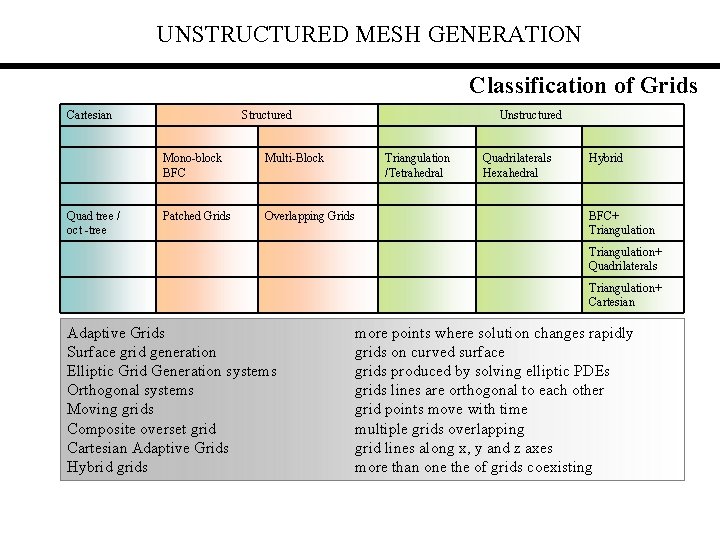
UNSTRUCTURED MESH GENERATION Classification of Grids Cartesian Quad tree / oct -tree Structured Mono-block BFC Multi-Block Patched Grids Overlapping Grids Unstructured Triangulation /Tetrahedral Quadrilaterals Hexahedral Hybrid BFC+ Triangulation+ Quadrilaterals Triangulation+ Cartesian Adaptive Grids Surface grid generation Elliptic Grid Generation systems Orthogonal systems Moving grids Composite overset grid Cartesian Adaptive Grids Hybrid grids more points where solution changes rapidly grids on curved surface grids produced by solving elliptic PDEs grids lines are orthogonal to each other grid points move with time multiple grids overlapping grid lines along x, y and z axes more than one the of grids coexisting

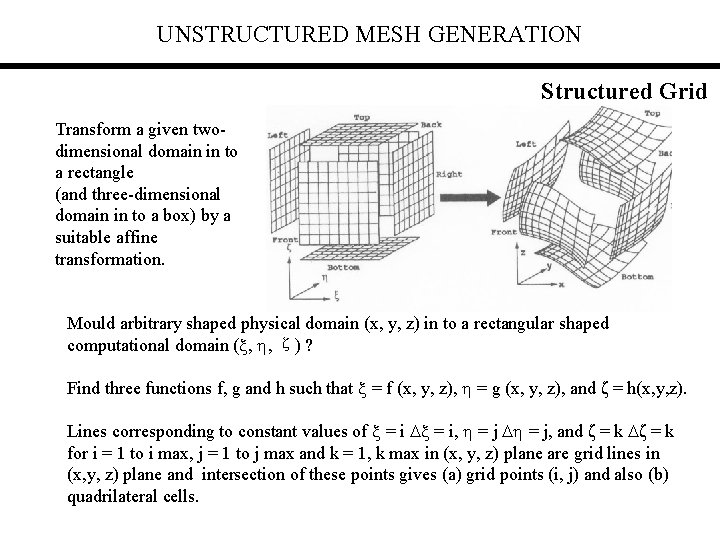
UNSTRUCTURED MESH GENERATION Structured Grid Transform a given twodimensional domain in to a rectangle (and three-dimensional domain in to a box) by a suitable affine transformation. = f (x, y) and = g (x, y). Mould arbitrary shaped physical domain (x, y, z) in to a rectangular shaped computational domain ( , , ζ) ? Find three functions f, g and h such that = f (x, y, z), = g (x, y, z), and ζ = h(x, y, z). Lines corresponding to constant values of = i, = j, and ζ = k for i = 1 to i max, j = 1 to j max and k = 1, k max in (x, y, z) plane are grid lines in (x, y, z) plane and intersection of these points gives (a) grid points (i, j) and also (b) quadrilateral cells.

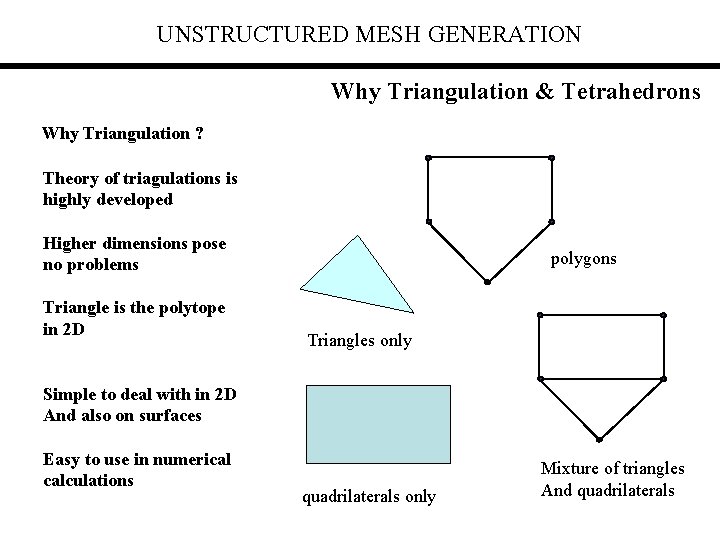
UNSTRUCTURED MESH GENERATION Why Triangulation & Tetrahedrons Why Triangulation ? Theory of triagulations is highly developed Higher dimensions pose no problems Triangle is the polytope in 2 D polygons Triangles only Simple to deal with in 2 D And also on surfaces Easy to use in numerical calculations quadrilaterals only Mixture of triangles And quadrilaterals

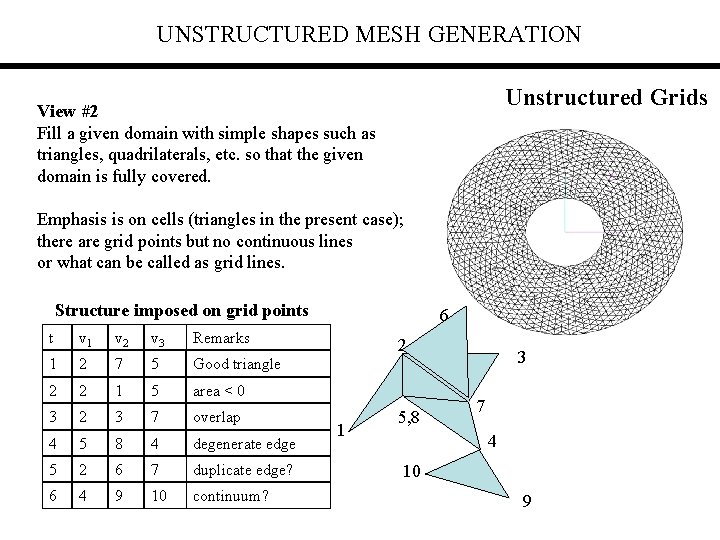
UNSTRUCTURED MESH GENERATION Unstructured Grids View #2 Fill a given domain with simple shapes such as triangles, quadrilaterals, etc. so that the given domain is fully covered. Emphasis is on cells (triangles in the present case); there are grid points but no continuous lines or what can be called as grid lines. Structure imposed on grid points t v 1 v 2 v 3 Remarks 1 2 7 5 Good triangle 2 2 1 5 area < 0 3 2 3 7 overlap 4 5 8 4 degenerate edge 5 2 6 7 duplicate edge? 6 4 9 10 continuum? 6 2 1 5, 8 3 7 4 10 9

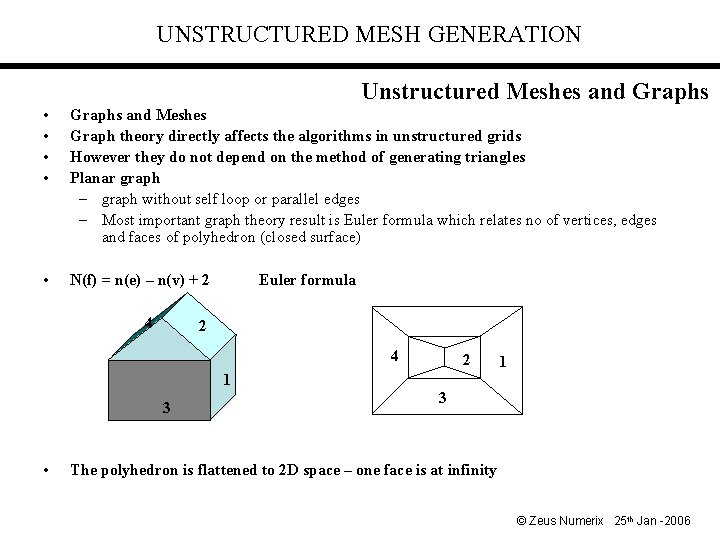
UNSTRUCTURED MESH GENERATION Unstructured Meshes and Graphs • • Graphs and Meshes Graph theory directly affects the algorithms in unstructured grids However they do not depend on the method of generating triangles Planar graph – graph without self loop or parallel edges – Most important graph theory result is Euler formula which relates no of vertices, edges and faces of polyhedron (closed surface) • N(f) = n(e) – n(v) + 2 4 Euler formula 2 4 2 1 1 3 • 3 The polyhedron is flattened to 2 D space – one face is at infinity © Zeus Numerix 25 th Jan -2006

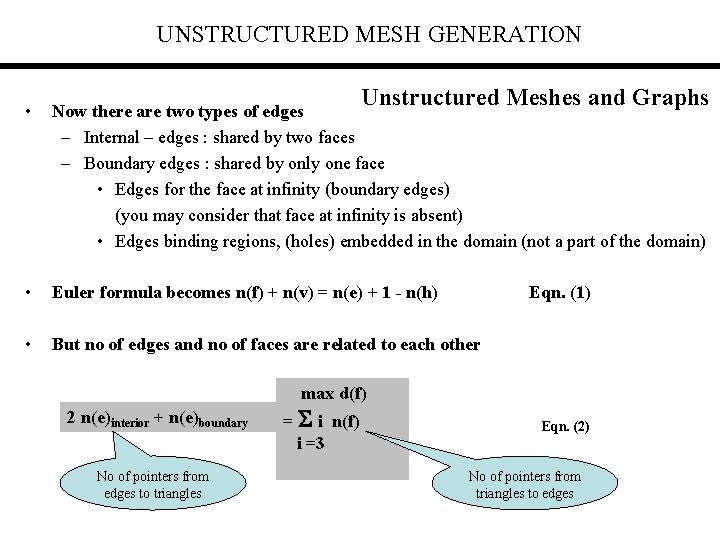
UNSTRUCTURED MESH GENERATION Unstructured Meshes and Graphs • Now there are two types of edges – Internal – edges : shared by two faces – Boundary edges : shared by only one face • Edges for the face at infinity (boundary edges) (you may consider that face at infinity is absent) • Edges binding regions, (holes) embedded in the domain (not a part of the domain) • Euler formula becomes n(f) + n(v) = n(e) + 1 - n(h) • But no of edges and no of faces are related to each other Eqn. (1) max d(f) 2 n(e)interior + n(e)boundary No of pointers from edges to triangles = i n(f) i =3 Eqn. (2) No of pointers from triangles to edges

UNSTRUCTURED MESH GENERATION Unstructured Meshes and Graphs Subtracting 2 time Eqn (1) from Eqn (3) n(f) = 2 n(v) - n(e)boundary -2 + 2 n(h) No of faces is approx. 2 times no of vertices Substituting for n(f) in Eqn. (1) n(e) = 3 n(v) - n(e)boundary - n(e) - 3 + 3 n(h) No of edges is approx. 3 time no of vertices! What can happen if n(f) 2 n(v) - n(e)boundary -2 + 2 n(h) n(e) 3 n(v) - n(e)boundary - n(e) - 3 + 3 n(h) or

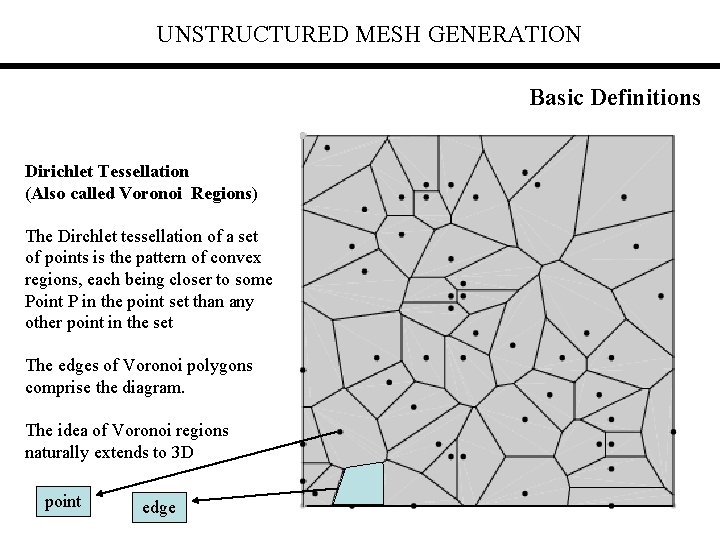
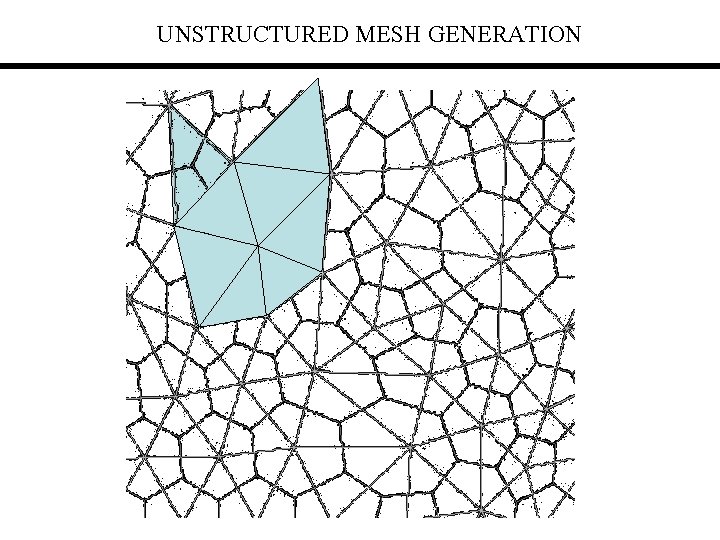
UNSTRUCTURED MESH GENERATION Basic Definitions Dirichlet Tessellation (Also called Voronoi Regions) The Dirchlet tessellation of a set of points is the pattern of convex regions, each being closer to some Point P in the point set than any other point in the set The edges of Voronoi polygons comprise the diagram. The idea of Voronoi regions naturally extends to 3 D point edge

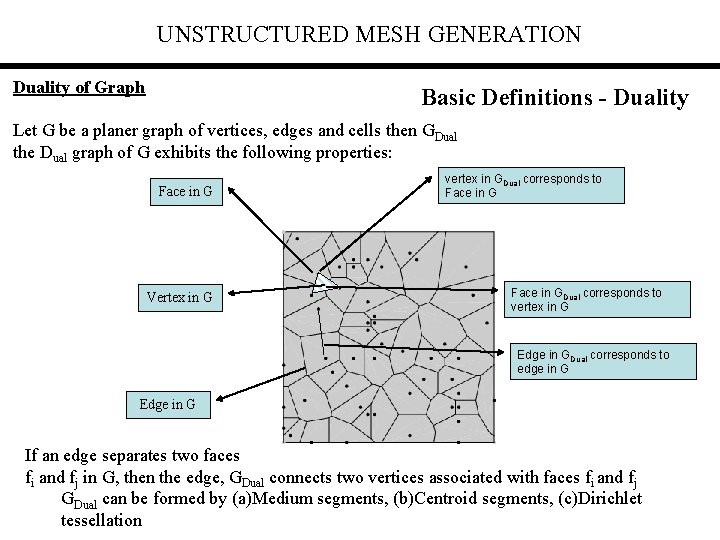
UNSTRUCTURED MESH GENERATION Duality of Graph Basic Definitions - Duality Let G be a planer graph of vertices, edges and cells then GDual the Dual graph of G exhibits the following properties: Face in G Vertex in G vertex in GDual corresponds to Face in GDual corresponds to vertex in G Edge in GDual corresponds to edge in G Edge in G If an edge separates two faces fi and fj in G, then the edge, GDual connects two vertices associated with faces fi and fj GDual can be formed by (a)Medium segments, (b)Centroid segments, (c)Dirichlet tessellation

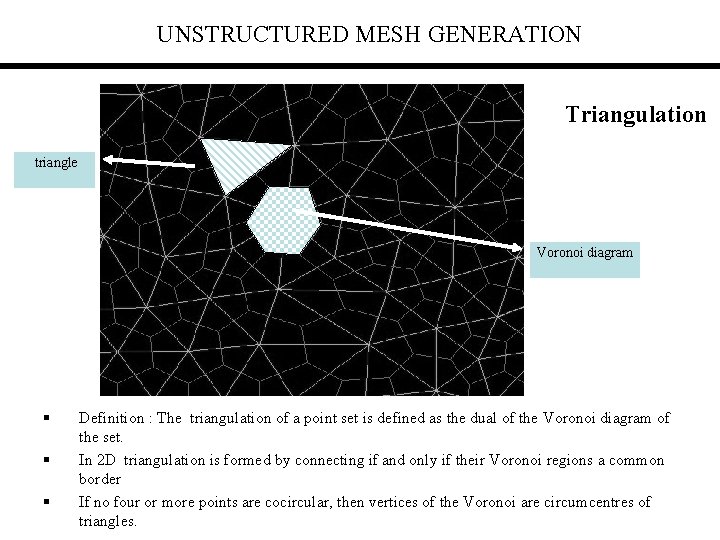
UNSTRUCTURED MESH GENERATION Triangulation triangle Voronoi diagram § § § Definition : The triangulation of a point set is defined as the dual of the Voronoi diagram of the set. In 2 D triangulation is formed by connecting if and only if their Voronoi regions a common border If no four or more points are cocircular, then vertices of the Voronoi are circumcentres of triangles.

UNSTRUCTURED MESH GENERATION Unstructured Meshes and Graphs Let use define N 0 = n(v), Vertices N 1 = n(e), edges N 2 = n(f), faces N 3 = n( ) volume Generalised Euler formula is d (-1)k N k= 0 (Euler formula in Rd); by definition N-1 = 1 k = -1 For the surface of polyhedron in 3 D, -1 + N 0 – N 1 + N 2 – 1 = 0 or N(f) + N(v) = N(e) +2 For polyhedral volumes n(f) + n(v) = n(e) + n( ) Like 2 D case this formula does not take care of boundary effects because it is valid for four-dimensional polytope

UNSTRUCTURED MESH GENERATION Geometric data : (x, y) coordinates of vertices Connectivity data : Vertex based Edge based Face based Data Structures v-v, v-e, v-f e-v, e-e, e-f f-v, f-e, f-f All 9 relations are not stored because Large RAM is required Consistency checks must be carried out on relations Only some relations are stored. All the remaining relations are derived from the stored relations The stored connectivity relations are called data structures: Some well-known data structures: Finite element data structure. Edge structure. Out-degree structure. Quad-edge structure. Winged-edge data structure.

UNSTRUCTURED MESH GENERATION Data Structures Storing of Structured grids in unique Edges in 3 D are always formed by (i+1, j, k) and (i, j, k) etc…. Faces are always formed by (i, j, k), (i+1, j, k), (I, j+1, k) and (i+1, j+1, k)… How to Store Unstructured Meshes? Collection of ensure does not ensure edges are connected Collection of faces does not ensure faces form a 3 D cell and that faces not intersecting. . .

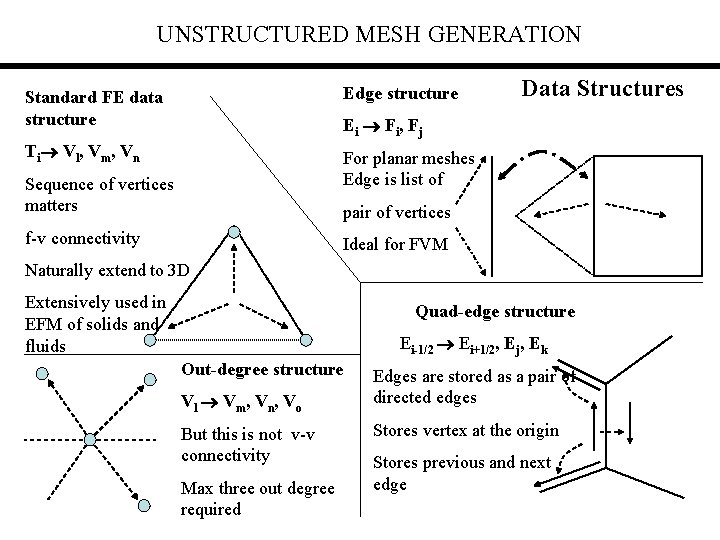
UNSTRUCTURED MESH GENERATION Standard FE data structure Edge structure Ti Vl, Vm, Vn For planar meshes Edge is list of Data Structures Ei Fi, Fj Sequence of vertices matters pair of vertices f-v connectivity Ideal for FVM Naturally extend to 3 D Extensively used in EFM of solids and fluids Quad-edge structure Ei-1/2 Ei+1/2, Ej, Ek Out-degree structure Vl Vm, Vn, Vo But this is not v-v connectivity Max three out degree required Edges are stored as a pair of directed edges Stores vertex at the origin Stores previous and next edge

UNSTRUCTURED MESH GENERATION Graph Operations on Unstructured Grids Planar Graph with Minimum Out-Degree Theorem: Every planar graph has a 3 bounded orientation; i. e. each edge of a planar graph can be assigned a direction such that the maximum number of edges pointing outward from any vertex is less than three Proof. • Find a vertex such that incident boundary edges that connected to at most maximum two. Other boundary vertices and any number of interior edges. • Such a vertex is called reducible vertex. It can be proved that at least two vertices always exit • • The two edges connected to boundary vertices are directed outward All the remaining edges are directed inward • The directed edges are removed from the graph • The process is repeated on the remaining graph

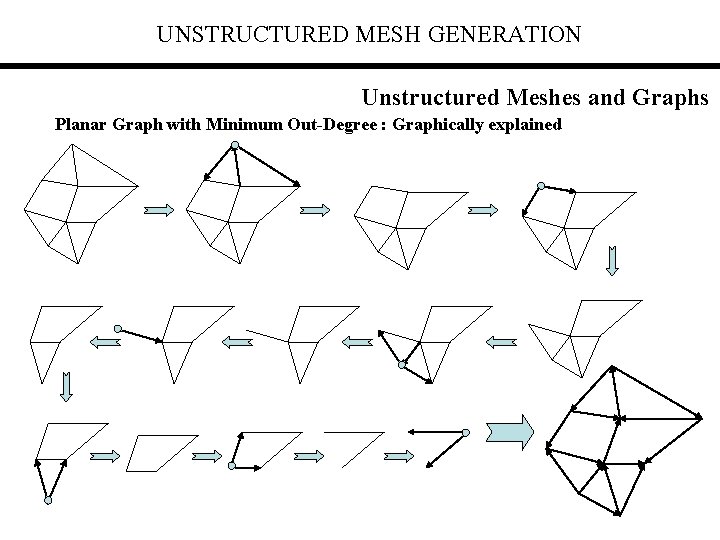
UNSTRUCTURED MESH GENERATION Unstructured Meshes and Graphs Planar Graph with Minimum Out-Degree : Graphically explained

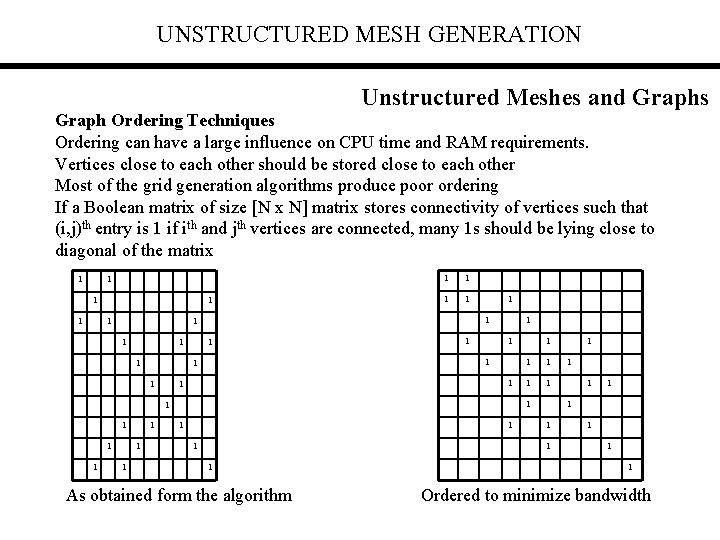
UNSTRUCTURED MESH GENERATION Unstructured Meshes and Graphs Graph Ordering Techniques Ordering can have a large influence on CPU time and RAM requirements. Vertices close to each other should be stored close to each other Most of the grid generation algorithms produce poor ordering If a Boolean matrix of size [N x N] matrix stores connectivity of vertices such that (i, j)th entry is 1 if ith and jth vertices are connected, many 1 s should be lying close to diagonal of the matrix 1 1 1 1 1 1 1 1 1 1 1 As obtained form the algorithm 1 1 1 Ordered to minimize bandwidth

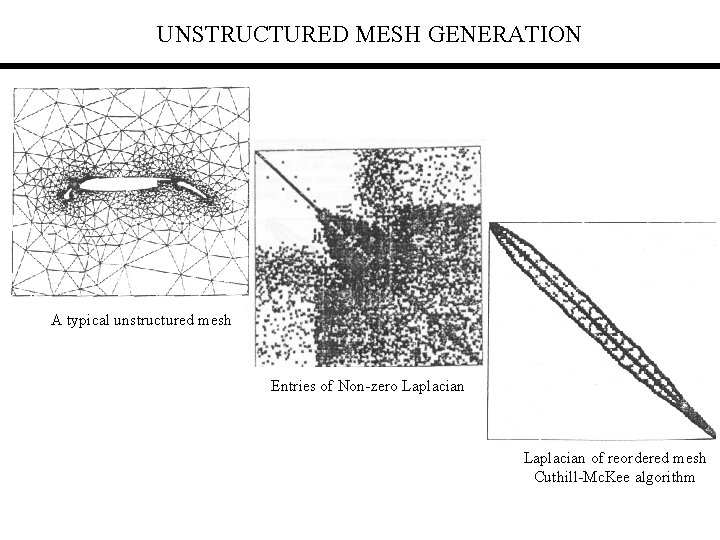
UNSTRUCTURED MESH GENERATION A typical unstructured mesh Entries of Non-zero Laplacian of reordered mesh Cuthill-Mc. Kee algorithm

UNSTRUCTURED MESH GENERATION Unstructured Meshes and Graphs Graph Ordering Techniques Rosen Algorithm Step I : Determine the band width and choose a pair of vertices (say i and j) such that i < j Step II : If increasing i or decreasing j reduces band width then (increase i or decrease j and goto Step I) Step III : If increasing i and decreasing j does not change the band width then (increase I or decrease j and goto Step I) Comments Produces good ordering but is very expensive especially for large graphs

UNSTRUCTURED MESH GENERATION Unstructured Meshes and Graphs Graph Ordering Techniques Cuthill-Mc. Kee Algorithm Step III Step IV Step V : Find the vertex with lowest degree : Find all the neighbouring vertices incident on root. : Order the neghbouring vertices by increasing degree : Choose the neighbour with lowest degree if not previously not ordered. : Continue with Step II till all vertices are ordered. Comments Very efficient Recommended in LD decomposition of matrices by reverse renumbering

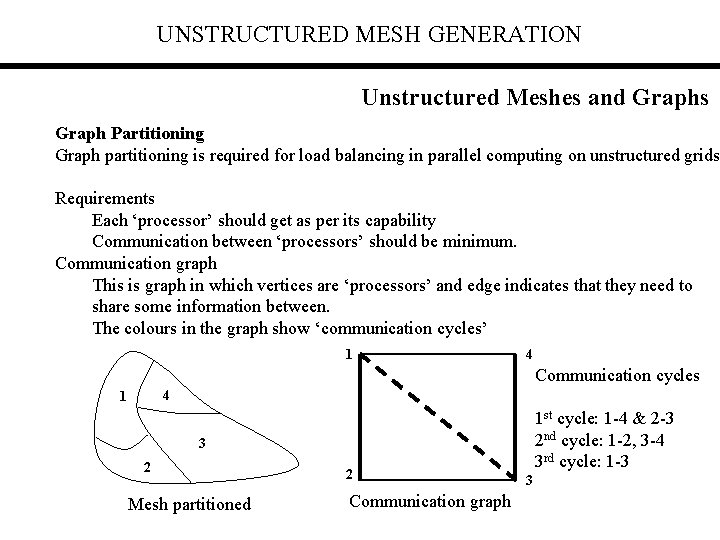
UNSTRUCTURED MESH GENERATION Unstructured Meshes and Graphs Graph Partitioning Graph partitioning is required for load balancing in parallel computing on unstructured grids Requirements Each ‘processor’ should get as per its capability Communication between ‘processors’ should be minimum. Communication graph This is graph in which vertices are ‘processors’ and edge indicates that they need to share some information between. The colours in the graph show ‘communication cycles’ 1 4 Communication cycles 4 1 1 st cycle: 1 -4 & 2 -3 2 nd cycle: 1 -2, 3 -4 3 rd cycle: 1 -3 3 2 Mesh partitioned 2 Communication graph 3

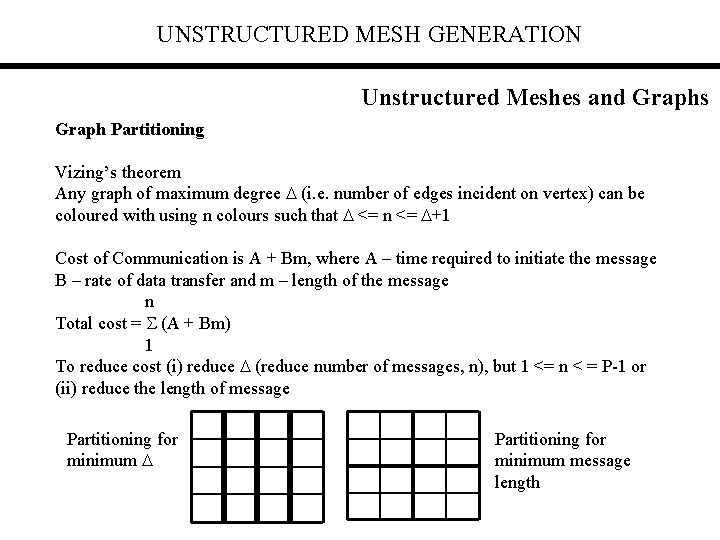
UNSTRUCTURED MESH GENERATION Unstructured Meshes and Graphs Graph Partitioning Vizing’s theorem Any graph of maximum degree (i. e. number of edges incident on vertex) can be coloured with using n colours such that <= n <= +1 Cost of Communication is A + Bm, where A – time required to initiate the message B – rate of data transfer and m – length of the message n Total cost = (A + Bm) 1 To reduce cost (i) reduce (reduce number of messages, n), but 1 <= n < = P-1 or (ii) reduce the length of message Partitioning for minimum message length

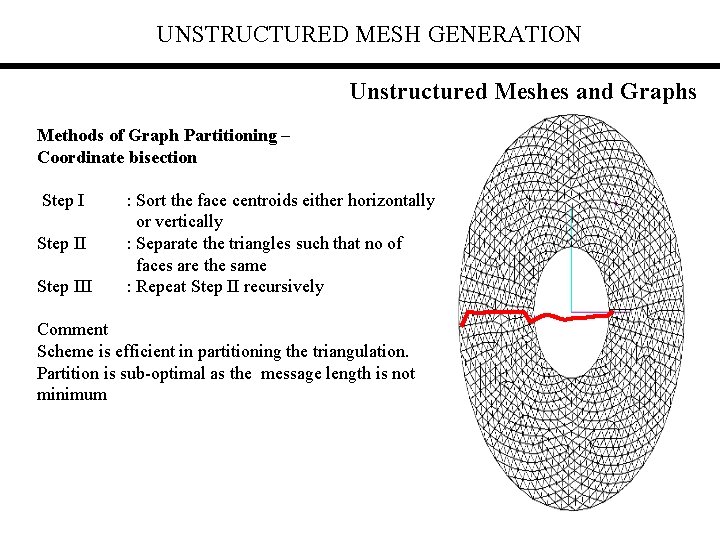
UNSTRUCTURED MESH GENERATION Unstructured Meshes and Graphs Methods of Graph Partitioning – Coordinate bisection Step III : Sort the face centroids either horizontally or vertically : Separate the triangles such that no of faces are the same : Repeat Step II recursively Comment Scheme is efficient in partitioning the triangulation. Partition is sub-optimal as the message length is not minimum

UNSTRUCTURED MESH GENERATION Unstructured Meshes and Graphs Methods of Graph Partitioning – Cut. Hill-Mc. Kee Algorithm Step III : Produce a dual of given mesh : Reorder the dual graph : Set the partition at the median or closet to the median Comment Scheme is efficient in partitioning the triangulation. Reduces number of sub-graphs Tends to produce sub-optimal as the message length is not minimum

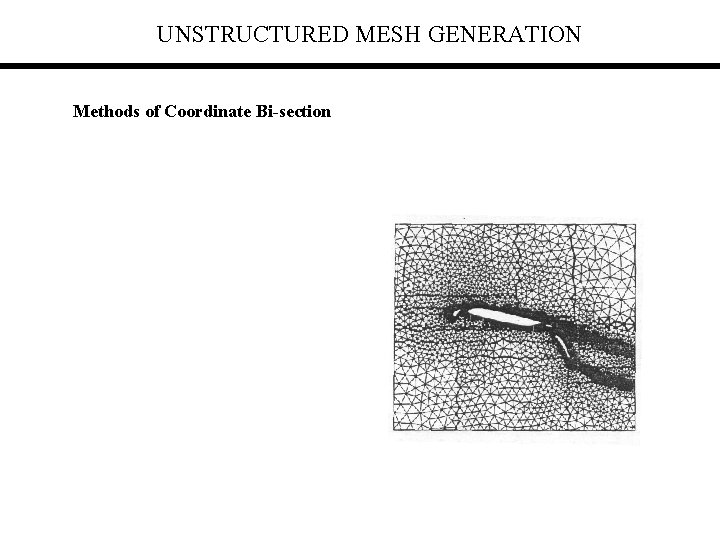
UNSTRUCTURED MESH GENERATION Methods of Coordinate Bi-section

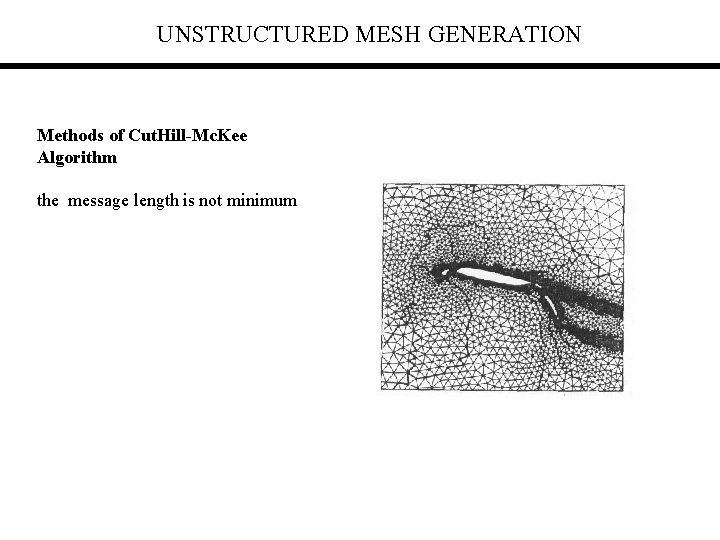
UNSTRUCTURED MESH GENERATION Methods of Cut. Hill-Mc. Kee Algorithm the message length is not minimum

UNSTRUCTURED MESH GENERATION Methods of Spectral Partitioning the message length is not minimum

UNSTRUCTURED MESH GENERATION

UNSTRUCTURED MESH GENERATION

UNSTRUCTURED MESH GENERATION

UNSTRUCTURED MESH GENERATION

UNSTRUCTURED MESH GENERATION

UNSTRUCTURED MESH GENERATION

UNSTRUCTURED MESH GENERATION

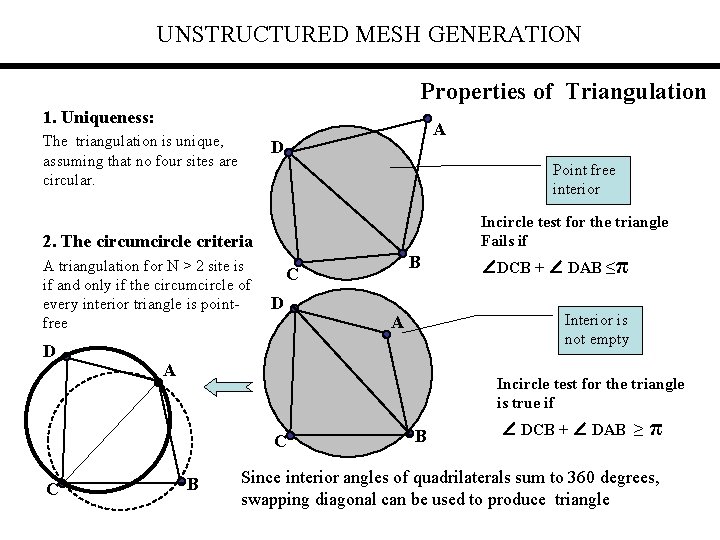
UNSTRUCTURED MESH GENERATION Properties of Triangulation 1. Uniqueness: The triangulation is unique, assuming that no four sites are circular. A D Point free interior Incircle test for the triangle Fails if 2. The circumcircle criteria A triangulation for N > 2 site is if and only if the circumcircle of every interior triangle is pointfree D D ∠DCB + ∠ DAB ≤π Interior is not empty A A Incircle test for the triangle is true if C C B B ∠ DCB + ∠ DAB ≥ π Since interior angles of quadrilaterals sum to 360 degrees, swapping diagonal can be used to produce triangle

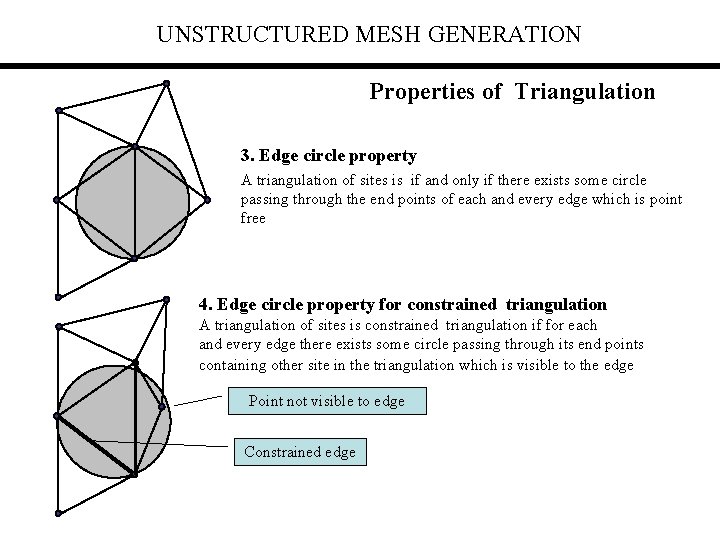
UNSTRUCTURED MESH GENERATION Properties of Triangulation 3. Edge circle property A triangulation of sites is if and only if there exists some circle passing through the end points of each and every edge which is point free 4. Edge circle property for constrained triangulation A triangulation of sites is constrained triangulation if for each and every edge there exists some circle passing through its end points containing other site in the triangulation which is visible to the edge Point not visible to edge Constrained edge

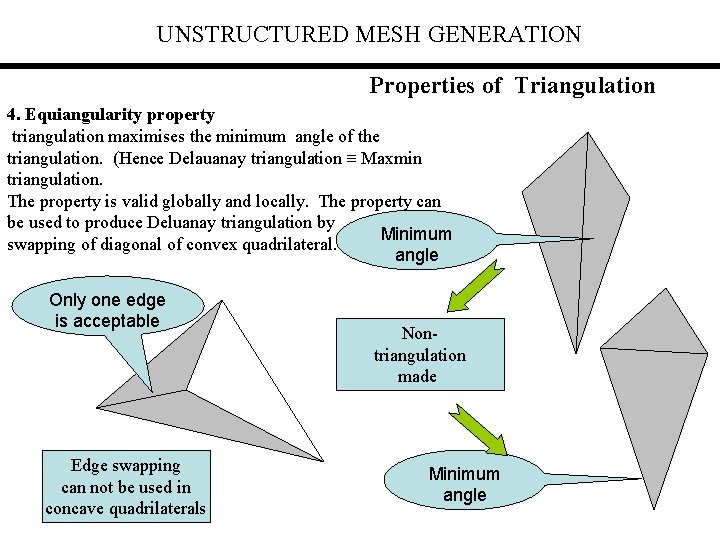
UNSTRUCTURED MESH GENERATION Properties of Triangulation 4. Equiangularity property triangulation maximises the minimum angle of the triangulation. (Hence Delauanay triangulation Maxmin triangulation. The property is valid globally and locally. The property can be used to produce Deluanay triangulation by Minimum swapping of diagonal of convex quadrilateral. angle Only one edge is acceptable Edge swapping can not be used in concave quadrilaterals Nontriangulation made Minimum angle

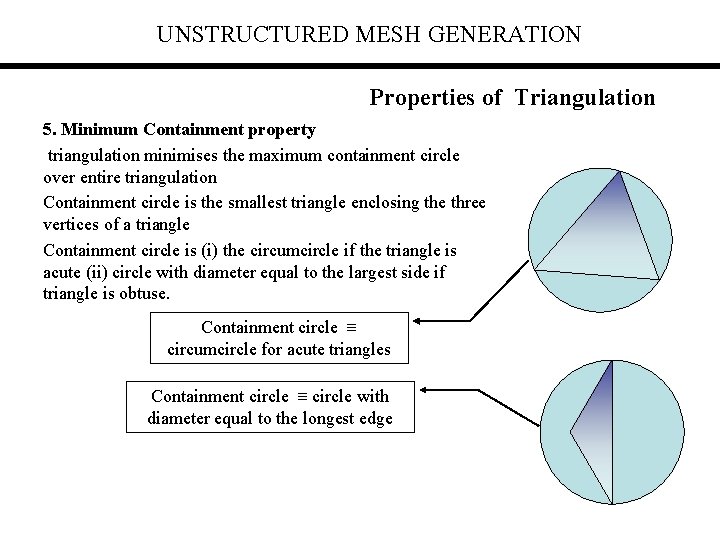
UNSTRUCTURED MESH GENERATION Properties of Triangulation 5. Minimum Containment property triangulation minimises the maximum containment circle over entire triangulation Containment circle is the smallest triangle enclosing the three vertices of a triangle Containment circle is (i) the circumcircle if the triangle is acute (ii) circle with diameter equal to the largest side if triangle is obtuse. Containment circle circumcircle for acute triangles Containment circle with diameter equal to the longest edge

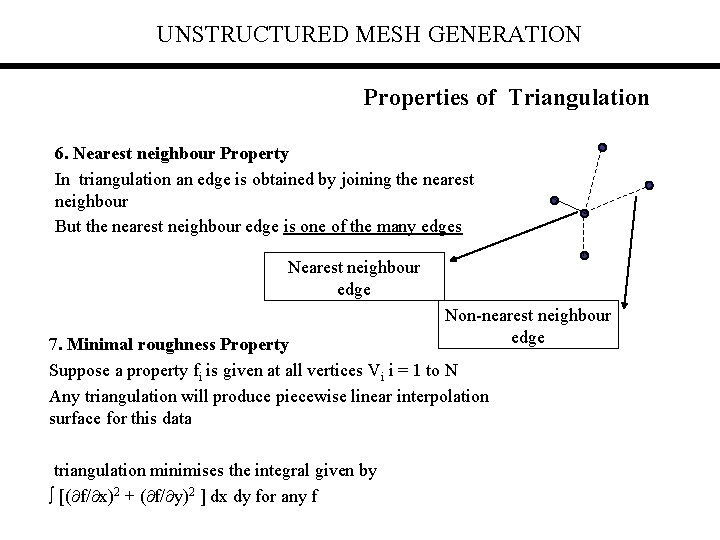
UNSTRUCTURED MESH GENERATION Properties of Triangulation 6. Nearest neighbour Property In triangulation an edge is obtained by joining the nearest neighbour But the nearest neighbour edge is one of the many edges Nearest neighbour edge Non-nearest neighbour edge 7. Minimal roughness Property Suppose a property fi is given at all vertices Vi i = 1 to N Any triangulation will produce piecewise linear interpolation surface for this data triangulation minimises the integral given by [( f/ x)2 + ( f/ y)2 ] dx dy for any f

UNSTRUCTURED MESH GENERATION Generation of Triangulation • • • Divide and conquer algorithm Incremental insertion algorithm – Bowyer algorithm – Watson algorithm – Green and Sibson algorithm Global edge swapping algorithm. Advancing front algorithm Graded triangulation algorithm

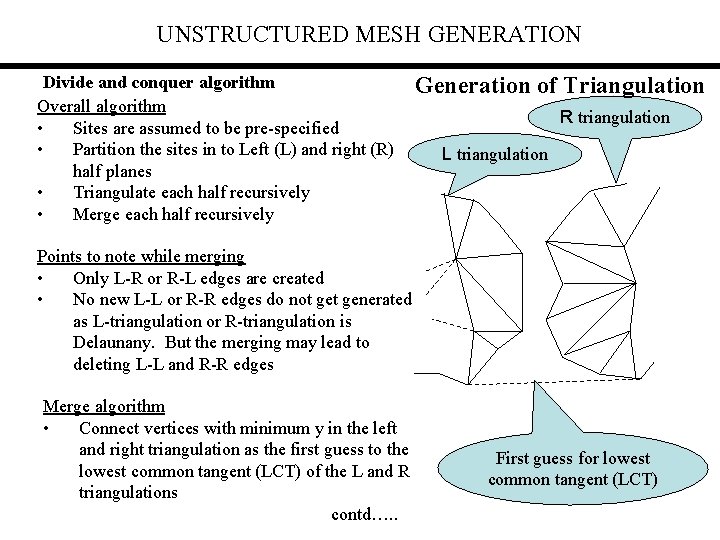
UNSTRUCTURED MESH GENERATION Divide and conquer algorithm Overall algorithm • Sites are assumed to be pre-specified • Partition the sites in to Left (L) and right (R) half planes • Triangulate each half recursively • Merge each half recursively Generation of Triangulation R triangulation L triangulation Points to note while merging • Only L-R or R-L edges are created • No new L-L or R-R edges do not generated as L-triangulation or R-triangulation is Delaunany. But the merging may lead to deleting L-L and R-R edges Merge algorithm • Connect vertices with minimum y in the left and right triangulation as the first guess to the lowest common tangent (LCT) of the L and R triangulations contd…. . First guess for lowest common tangent (LCT)

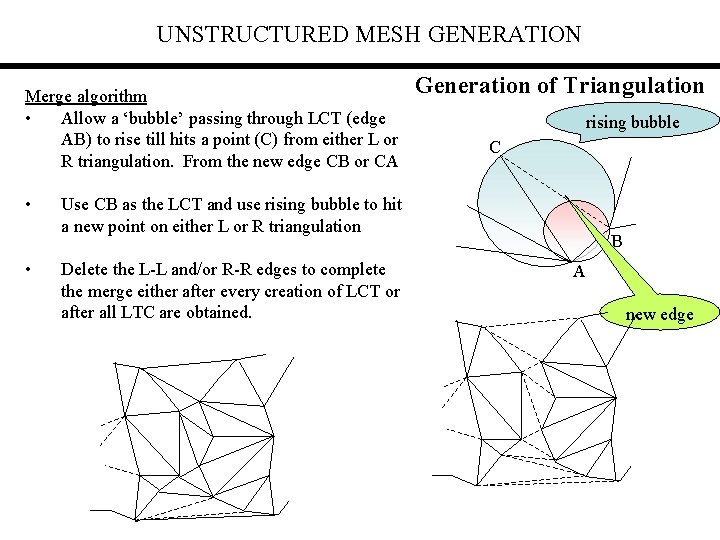
UNSTRUCTURED MESH GENERATION Merge algorithm • Allow a ‘bubble’ passing through LCT (edge AB) to rise till hits a point (C) from either L or R triangulation. From the new edge CB or CA • • Generation of Triangulation rising bubble C Use CB as the LCT and use rising bubble to hit a new point on either L or R triangulation Delete the L-L and/or R-R edges to complete the merge either after every creation of LCT or after all LTC are obtained. B A new edge

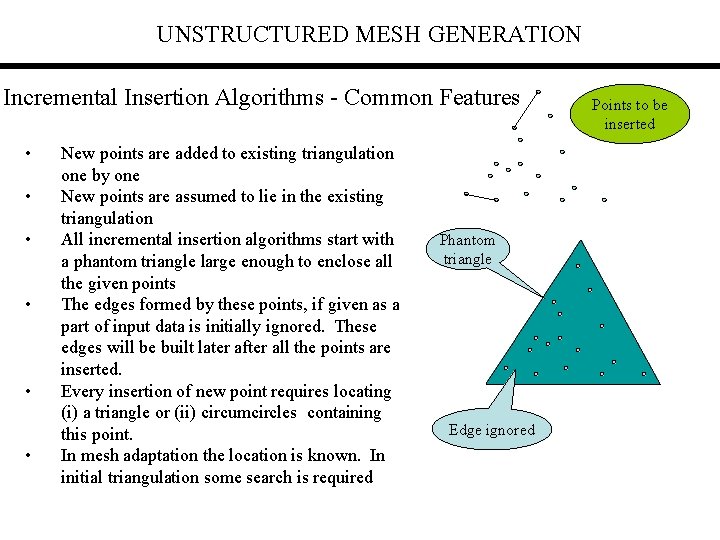
UNSTRUCTURED MESH GENERATION Incremental Insertion Algorithms - Common Features • • • New points are added to existing triangulation one by one New points are assumed to lie in the existing triangulation All incremental insertion algorithms start with a phantom triangle large enough to enclose all the given points The edges formed by these points, if given as a part of input data is initially ignored. These edges will be built later after all the points are inserted. Every insertion of new point requires locating (i) a triangle or (ii) circumcircles containing this point. In mesh adaptation the location is known. In initial triangulation some search is required Phantom triangle Edge ignored Points to be inserted

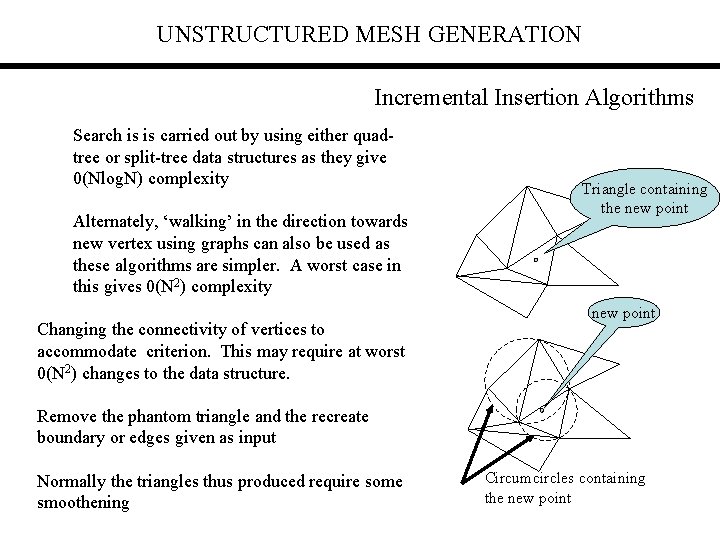
UNSTRUCTURED MESH GENERATION Incremental Insertion Algorithms Search is is carried out by using either quadtree or split-tree data structures as they give 0(Nlog. N) complexity Alternately, ‘walking’ in the direction towards new vertex using graphs can also be used as these algorithms are simpler. A worst case in this gives 0(N 2) complexity Changing the connectivity of vertices to accommodate criterion. This may require at worst 0(N 2) changes to the data structure. Triangle containing the new point Remove the phantom triangle and the recreate boundary or edges given as input Normally the triangles thus produced require some smoothening Circumcircles containing the new point

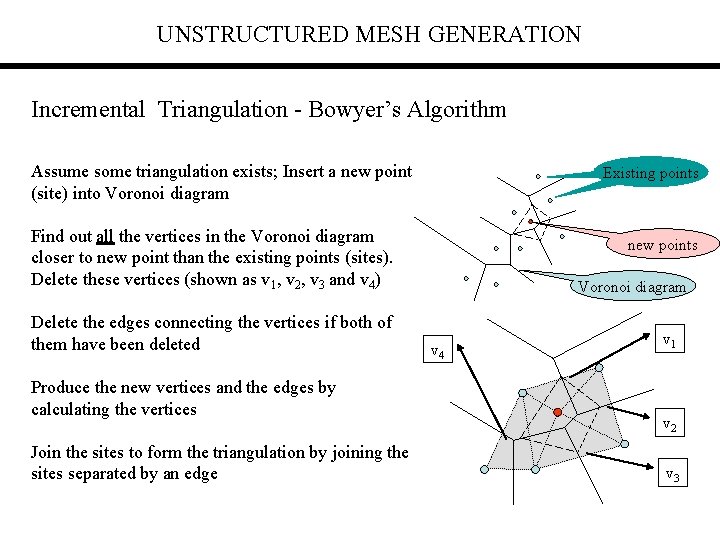
UNSTRUCTURED MESH GENERATION Incremental Triangulation - Bowyer’s Algorithm Assume some triangulation exists; Insert a new point (site) into Voronoi diagram Existing points Find out all the vertices in the Voronoi diagram closer to new point than the existing points (sites). Delete these vertices (shown as v 1, v 2, v 3 and v 4) Delete the edges connecting the vertices if both of them have been deleted Produce the new vertices and the edges by calculating the vertices Join the sites to form the triangulation by joining the sites separated by an edge new points Voronoi diagram v 4 v 1 v 2 v 3

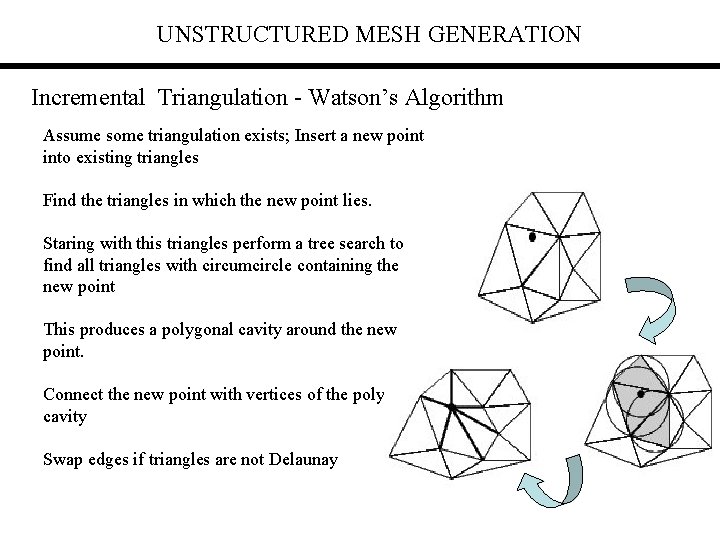
UNSTRUCTURED MESH GENERATION Incremental Triangulation - Watson’s Algorithm Assume some triangulation exists; Insert a new point into existing triangles Find the triangles in which the new point lies. Staring with this triangles perform a tree search to find all triangles with circumcircle containing the new point This produces a polygonal cavity around the new point. Connect the new point with vertices of the polygonal cavity Swap edges if triangles are not Delaunay

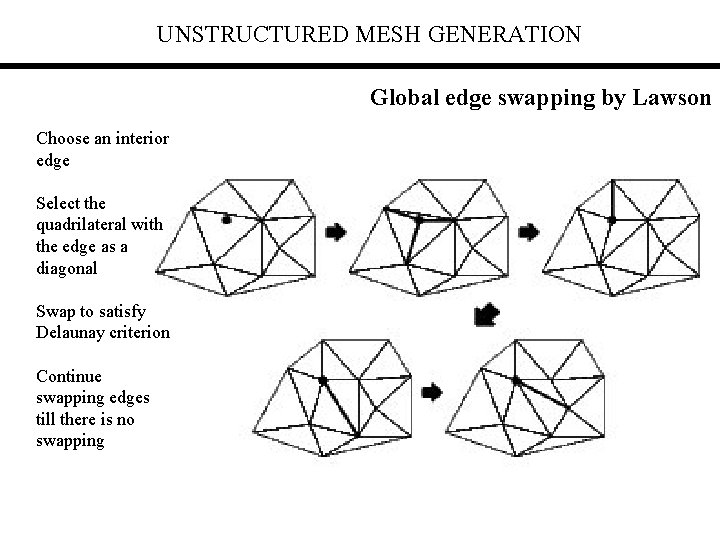
UNSTRUCTURED MESH GENERATION Global edge swapping by Lawson Choose an interior edge Select the quadrilateral with the edge as a diagonal Swap to satisfy Delaunay criterion Continue swapping edges till there is no swapping

UNSTRUCTURED MESH GENERATION Incremental Triangulation - Green and Sibson Algorithm Assume some triangulation exists; Insert a new point into existing triangles Find the triangles in which the new point lies. Create three additional edges by connecting the new point to the vertices of this triangle If the new point is on an edges, delete that and make four edges. The newly connected edges are always But the old edges do not remain Delauany; swap these edges recursively

UNSTRUCTURED MESH GENERATION Non- Methods of Triangulation These methods may or may not produce triangulation Triangulation is NOT essential from the point of view of FVM/FEM approximations It is essential that angles are not too close to 0 or 180 degrees are avoided Advancing Front Triangulation Min-Max Triangulation Greedy Triangulation Data Dependent Triangulation Steiner Triangulation Stretched Triangle Refinement

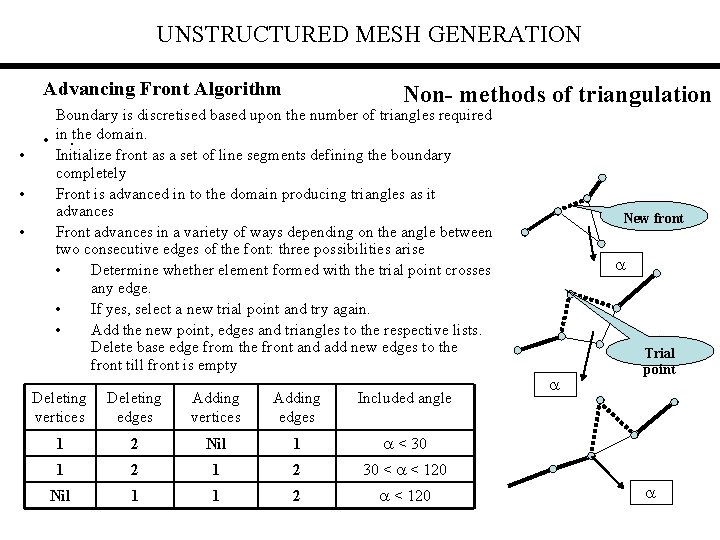
UNSTRUCTURED MESH GENERATION Advancing Front Algorithm 1. 2. 3. 4. 5. This method is particularly suited for the boundary representation of domains. Boundary is discretised based upon the number of triangles required in the domain. Initial front is a set of line segments defining the boundary completely. The edge to be deleted from the front is chosen based upon some criteria. For the edge to be deleted a) Select the trial point position. b) Search of any already existing point within a certain proximity of the trial point. If any such point exists then it becomes trial point. c) Determine whether element formed with the trial point crosses any edge. If yes, select a new trial point and try again. go to (b) 6. Add the new point, edges and triangles to the respective lists. 7. Delete base edge from the front and add new edges to the front. 8. If the front is non-empty, go to 4

UNSTRUCTURED MESH GENERATION Advancing Front Algorithm • • • Non- methods of triangulation Boundary is discretised based upon the number of triangles required • in. the domain. Initialize front as a set of line segments defining the boundary completely Front is advanced in to the domain producing triangles as it advances Front advances in a variety of ways depending on the angle between two consecutive edges of the font: three possibilities arise • Determine whether element formed with the trial point crosses any edge. • If yes, select a new trial point and try again. • Add the new point, edges and triangles to the respective lists. Delete base edge from the front and add new edges to the front till front is empty Deleting vertices Deleting edges Adding vertices Adding edges Included angle 1 2 Nil 1 < 30 1 2 30 < < 120 Nil 1 1 2 < 120 New front Trial point

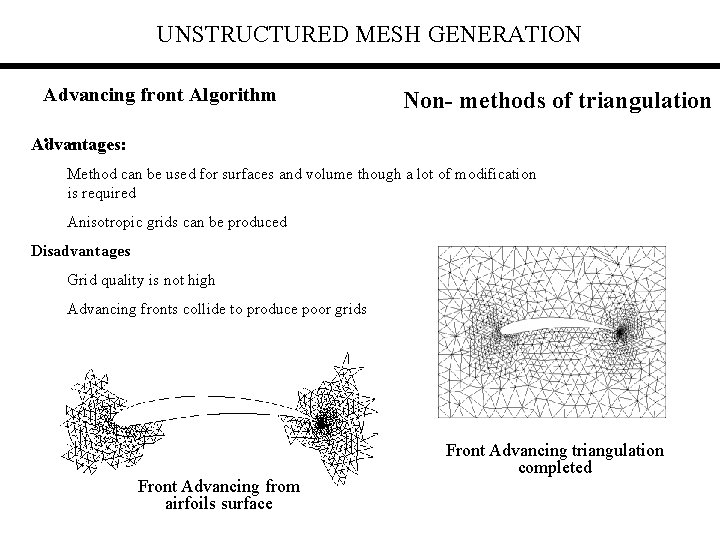
UNSTRUCTURED MESH GENERATION Advancing front Algorithm Non- methods of triangulation • . Advantages: Method can be used for surfaces and volume though a lot of modification is required Anisotropic grids can be produced Disadvantages Grid quality is not high Advancing fronts collide to produce poor grids Front Advancing from airfoils surface Front Advancing triangulation completed

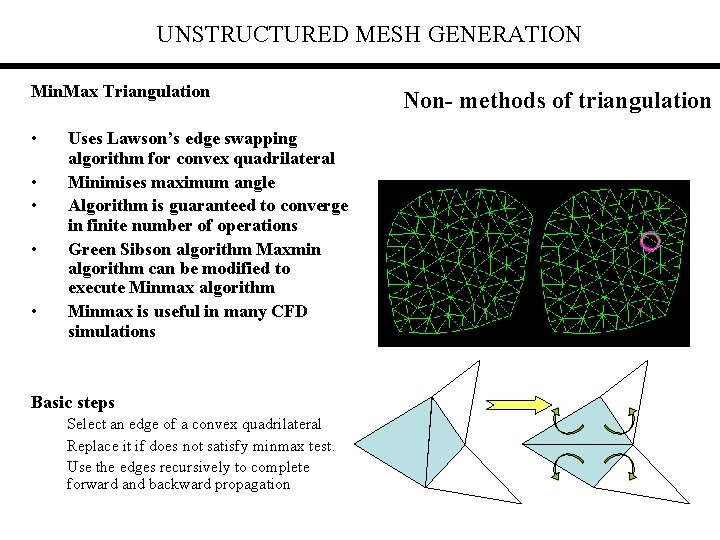
UNSTRUCTURED MESH GENERATION Min. Max Triangulation • • • Uses Lawson’s edge swapping algorithm for convex quadrilateral Minimises maximum angle Algorithm is guaranteed to converge in finite number of operations Green Sibson algorithm Maxmin algorithm can be modified to execute Minmax algorithm Minmax is useful in many CFD simulations Basic steps Select an edge of a convex quadrilateral Replace it if does not satisfy minmax test. Use the edges recursively to complete forward and backward propagation Non- methods of triangulation

UNSTRUCTURED MESH GENERATION Stretched Triangulation For some simulations equilateral triangular is not the choice of triangulation (e. g. viscous flow simulations) produces equilateral triangulation Stretched triangulation can be considered as a special case of Steiner triangulation Steiner point is inserted based stretching property demanded Algorithm Choose one dimensional stretching function r = f(distance perpendicular to boundary) Choose an existing triangulation Find a point on the boundary (vboundary) closed to each vertex (v) in the triangulation Store the distance between these two pints as S Choose a major given by Maximum dimension of the triangle projected along the perpendicular direction to boundary divided by r

UNSTRUCTURED MESH GENERATION Greedy Triangulation Here triangles never undoes what it has done before! Keep adding edges, but do not check quality of triangulation Triangulation satisfies Euler equation Normally used for producing triangle with shortest edge length Basic steps Start with initial triangulation with boundary edges listed Connect all the vertices to all other vertices to form additional edges Order the edges according to their length Choose the smallest edge If it does not interest any edge triangulation add to edges of the triangulation Keep choosing the next edge form the set of ordered edges till Euler equation is satisfied

UNSTRUCTURED MESH GENERATION Data dependent Triangulation Best triangulation for the given data defined at vertices is required Best edge is defined based either (a) on value of the jump in normal derivative (JND); the best edge has least jump or (b) Included angle between normals (ABN) If equation for property P with equations defining these properties as P 1 = a 1 x + b 1 y + c 1 and P 2 = a 2 x + b 2 y + c 2 then JND cost function = | nx(a 1 – a 2) + ny (b 1 – b 2) + nz (c 1 – c 2) | and ABN cost function = (a 1 a 2 + b 1 b 2 + 1)/ [(a 12 + b 12 +1)(a 22 + b 22 + 1)] Edges are swapped to minimise JND or ABN summed up over all edges

UNSTRUCTURED MESH GENERATION Steiner Triangulation By definition Steiner triangulation is any triangulation that adds additional sites to an existing triangulation to improve its measure of quality Every Steiner triangulation requires a strategy to insert a point Some of the strategies are: Equilateral triangles – Good for Inviscid flows Smooth area variation Triangles with minimum ration of circumcircle to incircle diameters – Good for viscous flows Circumcircle Refinement Place the new site in a position that guaranties no other site in the triangulation can lie Closer than the radius of the circumcircle. This produces sites as far as possible form existing sites Algorithm Construct triangulation of boundary points Compute the quality of each triangle such (e. g. area / ration of area/(ava. Area of neighbouring triangles, etc. ) If quality of all triangles is acceptable stop triangulation Otherwise choose the worst triangle and insert a point at its circumcentre and produce new triangulation

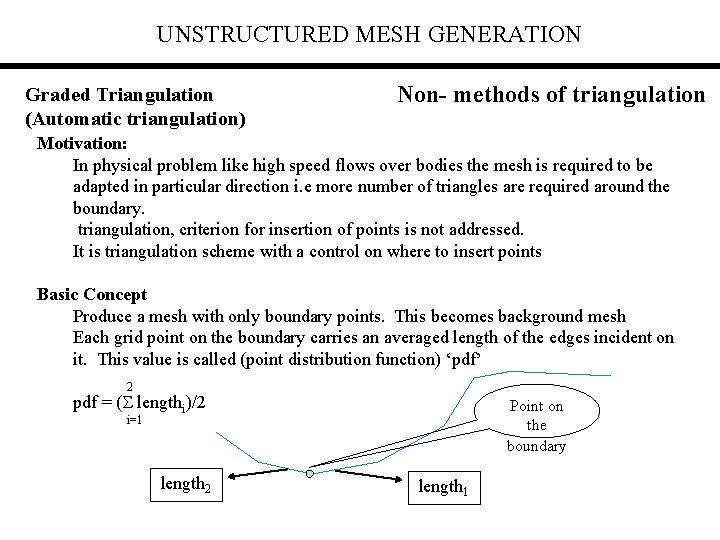
UNSTRUCTURED MESH GENERATION Graded Triangulation (Automatic triangulation) Non- methods of triangulation Motivation: In physical problem like high speed flows over bodies the mesh is required to be adapted in particular direction i. e more number of triangles are required around the boundary. triangulation, criterion for insertion of points is not addressed. It is triangulation scheme with a control on where to insert points Basic Concept Produce a mesh with only boundary points. This becomes background mesh Each grid point on the boundary carries an averaged length of the edges incident on it. This value is called (point distribution function) ‘pdf’ 2 pdf = ( lengthi)/2 Point on the boundary i=1 length 2 length 1

UNSTRUCTURED MESH GENERATION Graded Triangulation (Automatic triangulation) • Non- methods of triangulation The length of the new trial point from the edge of front is calculated as –. L = *L 1 + ß*L 2 + *L 3. • where ( , ß, ) are called barycentric coordinates. and +ß+ =1 L 1, L 2, L 3 are mesh densities at nodes of the triangle containing the trial point. • Mesh density at any node is defined as the mean of the lengths of the edges meeting at that point. • The barycentric coordinates ( , ß, ) are the ratios of the area of the three triangles formed by the trial point and the background triangle to the area of the background triangle.

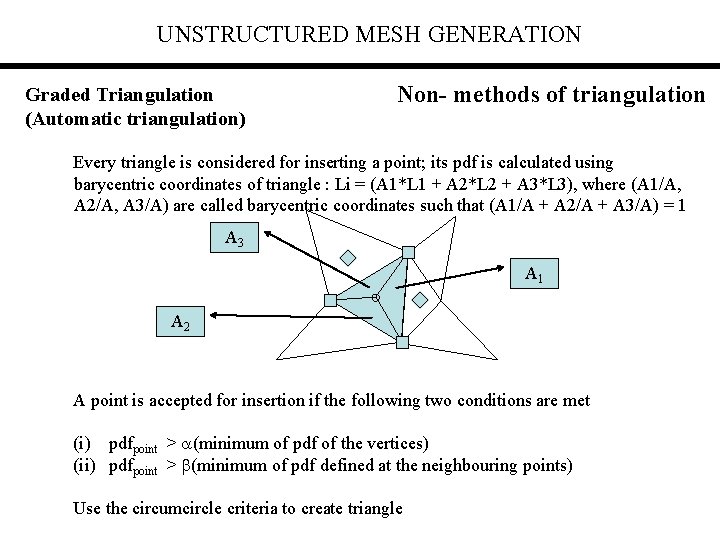
UNSTRUCTURED MESH GENERATION Graded Triangulation (Automatic triangulation) Non- methods of triangulation Every triangle is considered for inserting a point; its pdf is calculated using barycentric coordinates of triangle : Li = (A 1*L 1 + A 2*L 2 + A 3*L 3), where (A 1/A, A 2/A, A 3/A) are called barycentric coordinates such that (A 1/A + A 2/A + A 3/A) = 1 A 3 A 1 A 2 A point is accepted for insertion if the following two conditions are met (i) pdfpoint > (minimum of pdf of the vertices) (ii) pdfpoint > (minimum of pdf defined at the neighbouring points) Use the circumcircle criteria to create triangle