Voronoi Diagrams and Delaunay Triangulations Generalized spaces and

Voronoi Diagrams and Delaunay Triangulations Generalized spaces and distances

Generalized spaces

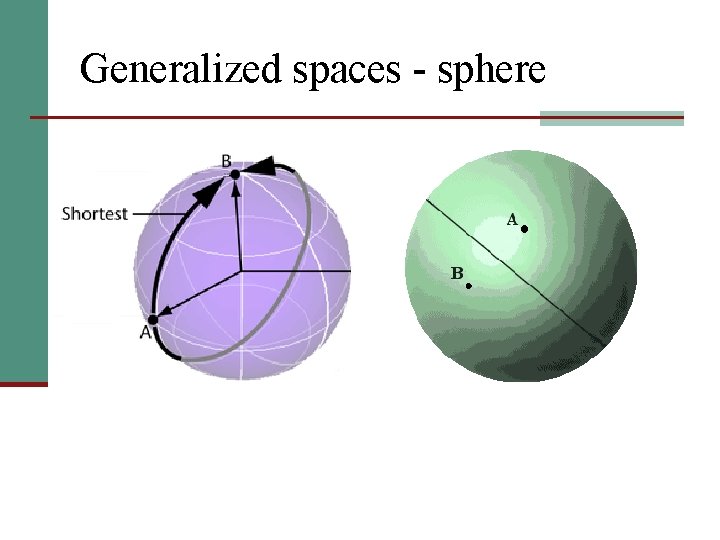
Generalized spaces - sphere

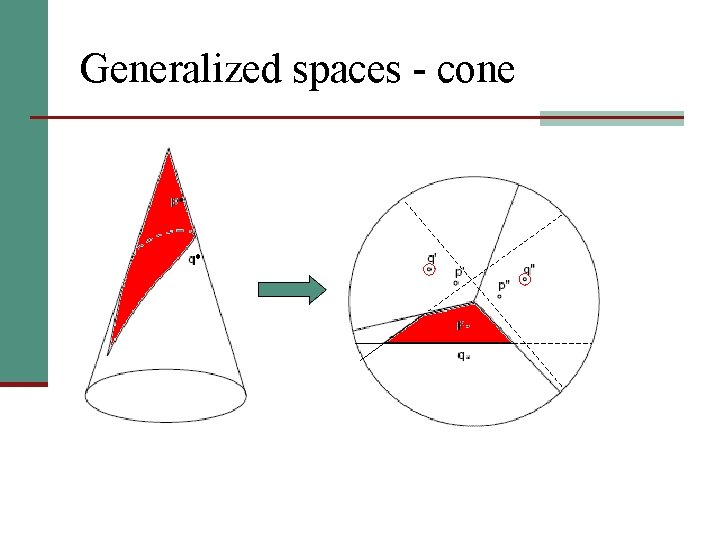
Generalized spaces - cone

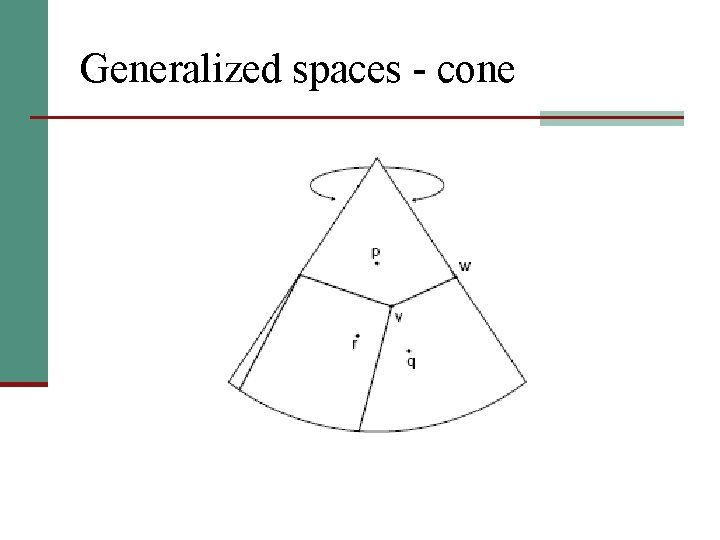
Generalized spaces - cone

Generalized spaces – orbits & quotient space n Let P denote the Euclidean plane and let G be a discrete group of motions on P: a group of bijections, s. t: n n

Generalized spaces – orbits & quotient space n Definitions: n Two points p, p’∈P are equivalent if n The equivalence class, [p], of p is called the orbit of p. n The quotient space, P/G, consists of all orbits. n A connected subset of P that contains a representative out of every orbit called a fundamental domain, if it is convex. n Lemma [Ehrlich and Im Hof]: Let p be a point of P that is left fixed only by the unit element of G. Then its Voronoi region VR(p, [p]) is a fundamental domain.

Generalized spaces – Voronoi diagram of quotient space n Let S 0 denote a set of representatives of S in a fundamental domain D⊂P. n Compute the Voronoi diagram V([S 0]), skipping all Voronoi edges that separate points of the same orbit. n Intersect the resulting structure with the fundamental domain D.

Convex distance functions

Convex distance functions

Convex distance functions n Definition: the set of all points q satisfying d(0, q)≤ 1 is the unit circle. n Properties: The value of d. C(p, q) does not change if both p and q are translated by the same vector. n the triangle inequality: d. C(p, r)≤d. C(p, q)+d. C(q, r) n d. C(p, q)=d. C’(q, p) , where C’ denotes the reflected image of C about the origin. n

Convex distance functions n Definition: Norm p is a function p: V→ℝ s. t: n p(x)≥ 0 (p(x)=0 x=0) p(λx)=|λ| p(x) n p(x+y)≤p(x)+p(y) n n If the set C is symmetric about the origin then d. C is a norm in the plane. n Well-known is the family of Lp (or: Minkowski) norms, p≥ 1, defined by the equation

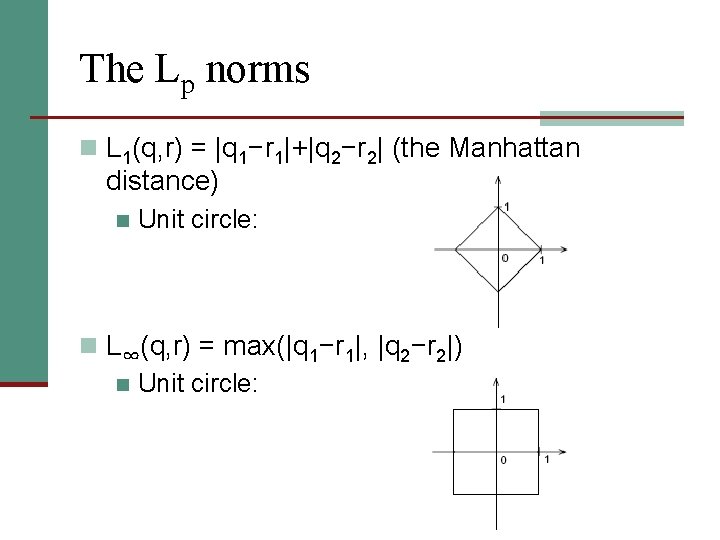
The Lp norms n L 1(q, r) = |q 1−r 1|+|q 2−r 2| (the Manhattan distance) n Unit circle: n L∞(q, r) = max(|q 1−r 1|, |q 2−r 2|) n Unit circle:

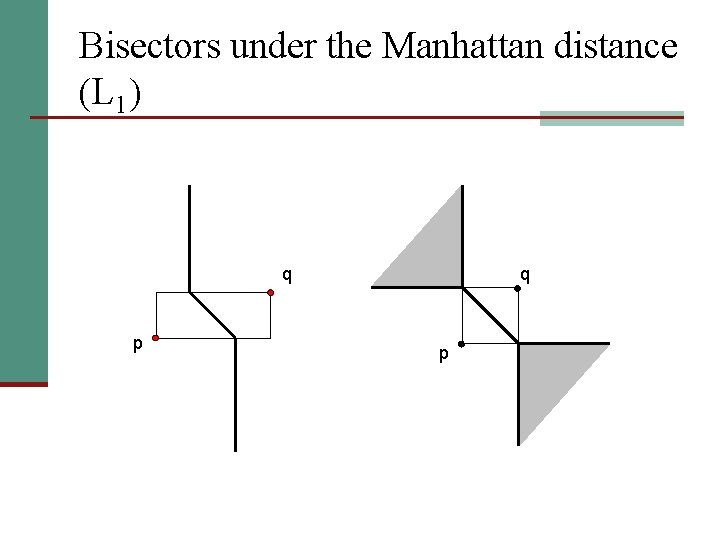
Bisectors under the Manhattan distance (L 1) q p

Strictly convex distance function n Each bisector B(p, q) is a curve homeomorphic to a line. n The strict triangle inequality holds. n Two circles with respect to d. C intersect in at most two points. n Two bisectors B(p, q), B(p, r) intersect in at most one point.

Voronoi diagrams under CD function n Voronoi regions are in general not convex. n Voronoi regions are star-shaped: For each point x∈D(p, q), the line segment px is also contained in D(p, q).

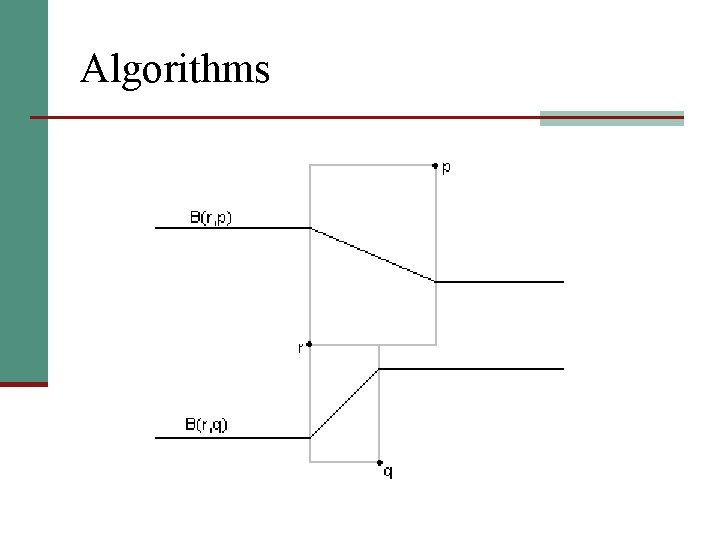
Algorithms

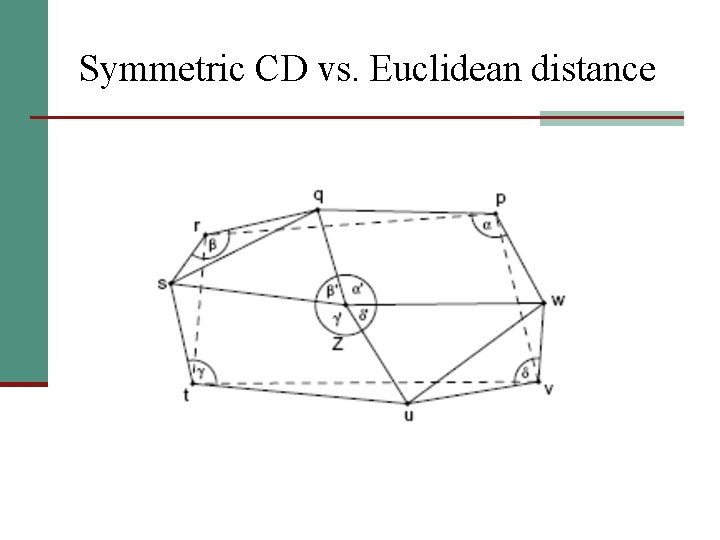
Symmetric CD vs. Euclidean distance n Symmetric CD is equivalent to the Euclidean distance in the sense that: n But:

Symmetric CD vs. Euclidean distance Theorm [Corbalan, Mazon, Recio, and Santos]: If for each set S of at most 4 points the Voronoi diagram VC(S) has the same combinatorial structure as VD(f(S)), for some bijection f of the plane, then f is linear and f(C) = D holds, up to scaling.

Symmetric CD vs. Euclidean distance

CD function in higher dimensions n Properties in 3 -space: n The bisector B(p, q) of two points is a surface homeomorphic to the plane. n Two bisector surfaces B(p, q), B(p, r) have an intersection homeomorphic to the line, or empty. n Theorem [Icking, Klein, Lê and Ma]: For each n>0 there exist C and 4 points s. t. there are 2 n+1 homothetic copies of C containing these points in their boundaries. n The Voronoi diagram of n points in 3 -space based on the L 1 norm is of complexity Θ(n 2), and the diagram in d-space based on L∞ are of complexity Θ(n�d/2�).

Metrics

Metrics n Metric, m, associates with any two points, p and q, a non-negative real number m(p, q). n Properties: m(p, q) = 0 ⇔ p = q. n m(p, q) = m(q, p). n The triangle inequality m(p, r)≤m(p, q)+m(q, r) holds. n

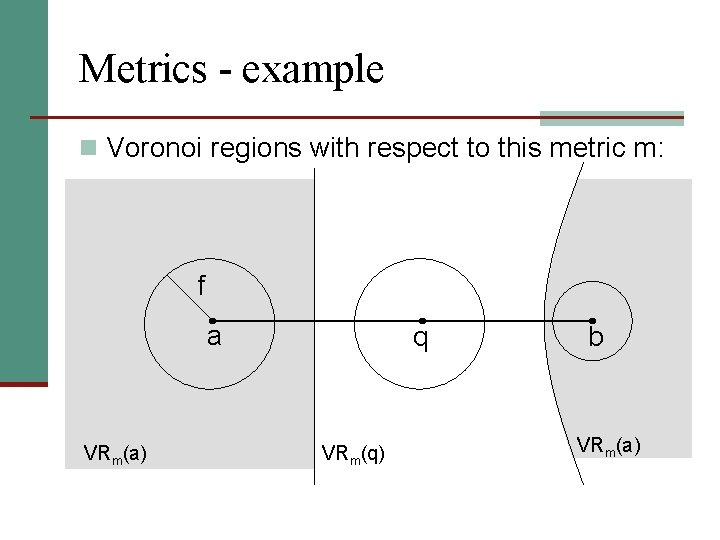
Metrics - example n Suppose there is an air-lift between two points a, b in the plane. Then

Metrics - example n Voronoi regions with respect to this metric m: f a VRm(a) q VRm(q) b VRm(a)

Nice metrics n Definition: A metric m in the plane is called nice if it enjoys the following properties: n A sequence pi converges to p under m iff this holds under the Euclidean distance. n For any two points p, r there exists a point q different from p and r s. t. m(p, r)=m(p, q)+m(q, r). n For any two points p, q: Bm(p, q) is a curve homeomorphic to the line. n The intersection of two bisector curves consists of only finitely many connected components.

Nice metrics n Lemma [Menger]: Let m be a nice metric in the plane. Then for any two points p, r there exists a path π connecting them, such that for each point q on π: m(p, r)=m(p, q)+m(q, r).

Voronoi diagrams based on nice metrics n Lemma (m-star-shaped): Let m be a nice metric. Then each Voronoi region VRm(p, S) is connected: Each mstraight path π from p to some point x∈VRm(p, S) is fully contained in VRm(p, S).

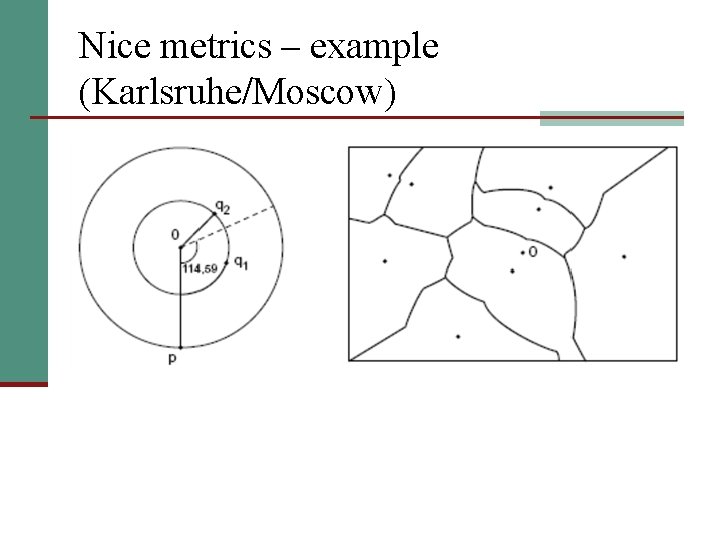
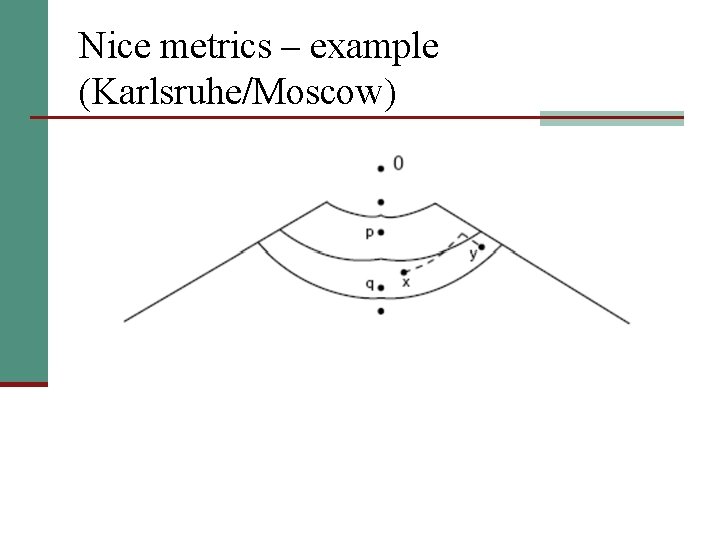
Nice metrics – example (Karlsruhe/Moscow)

Nice metrics – example (Karlsruhe/Moscow)

Algorithms n Theorem [Dehne and Klein]: The Voronoi diagram of n point sites under a nice metric in the plane can be constructed within O(nlogn) many steps, using the sweep line approach.

General Voronoi diagrams

Edelsbrunner and Seidel approach n Given: n S, a set of indices {1, 2, …}. n A fixed domain, X. n For each i∈S a real-valued function fi: X→ℝ. n is a hypersurface in the space X╳ℝ. n The Voronoi diagram is the projection onto X of the lower envelope:

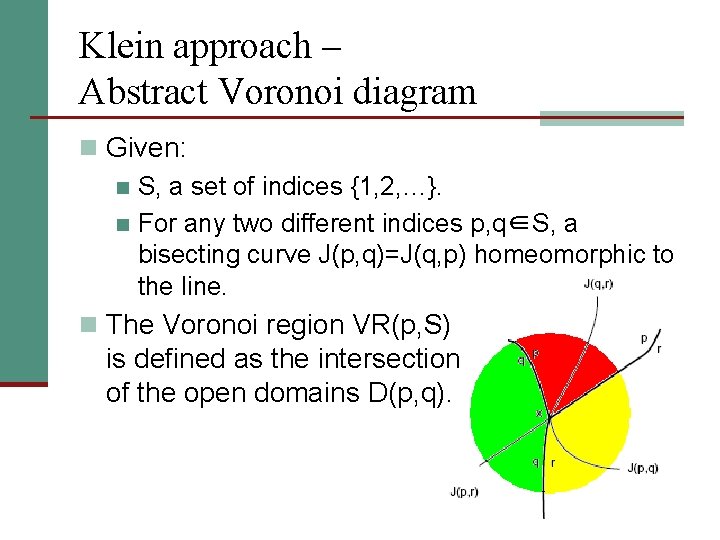
Klein approach – Abstract Voronoi diagram n Given: n S, a set of indices {1, 2, …}. n For any two different indices p, q∈S, a bisecting curve J(p, q)=J(q, p) homeomorphic to the line. n The Voronoi region VR(p, S) is defined as the intersection of the open domains D(p, q).

Admissible system n Definition: The system is called admissible iff for each S’⊆S of size at least 3 the following conditions are fulfilled: The Voronoi regions are connected. n Each point of the plane lies in a Voronoi region (or on the Voronoi diagram). n The intersection of two curves consists of only finitely many components. n

Admissible system n Lemma: Let ℐ be an admissible system, and suppose that J(p, q) and J(p, r) cross at the point x. Then J(q, r) also passes through x.

Computing diagram of admissible system n Divide & conquer ☑ n Randomized incremental ☑ n Sweep ☒

Questions? Thank you!