An Introduction to Computational Geometry Voronoi and Delaunay

An Introduction to Computational Geometry: Voronoi and Delaunay Diagrams Joseph S. B. Mitchell Stony Brook University Chapters 3, 4: Devadoss-O’Rourke

Voronoi Diagrams Georgy Voronoi 1868 -1908

Historical Origins and Diagrams in Nature René Descartes 1596 -1650 1644: Gravitational Influence of stars Dragonfly wing Giraffe pigmentation Honeycomb Ack: Streinu&Brock Constrained soap bubbles 3

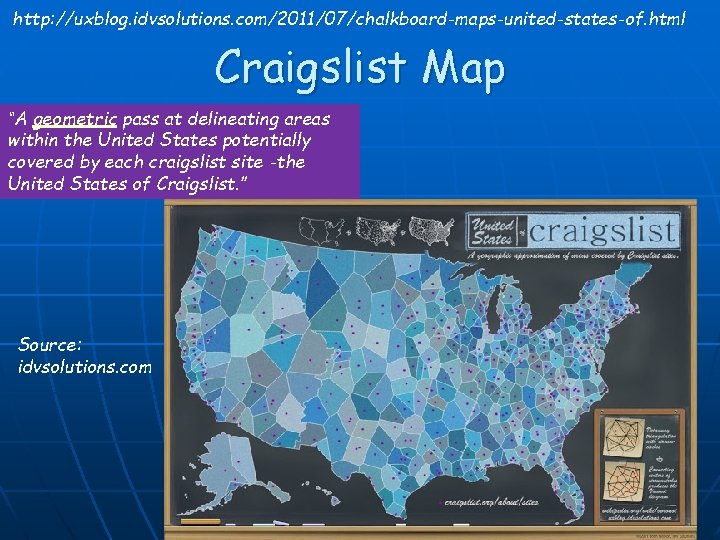
http: //uxblog. idvsolutions. com/2011/07/chalkboard-maps-united-states-of. html Craigslist Map “A geometric pass at delineating areas within the United States potentially covered by each craigslist site -the United States of Craigslist. ” Source: idvsolutions. com 4

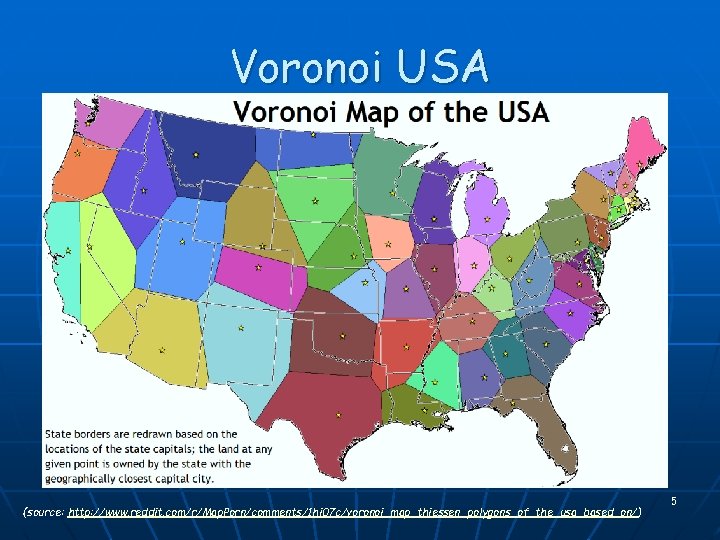
Voronoi USA (source: http: //www. reddit. com/r/Map. Porn/comments/1 hi 07 c/voronoi_map_thiessen_polygons_of_the_usa_based_on/) 5

Voronoi Applications n n n Voronoi, together with point location search: nearest neighbor queries Facility location: Largest empty disk (centered at a Voronoi vertex) Shape description/approximation: medial axis [Lecture 12, David Mount notes] 6

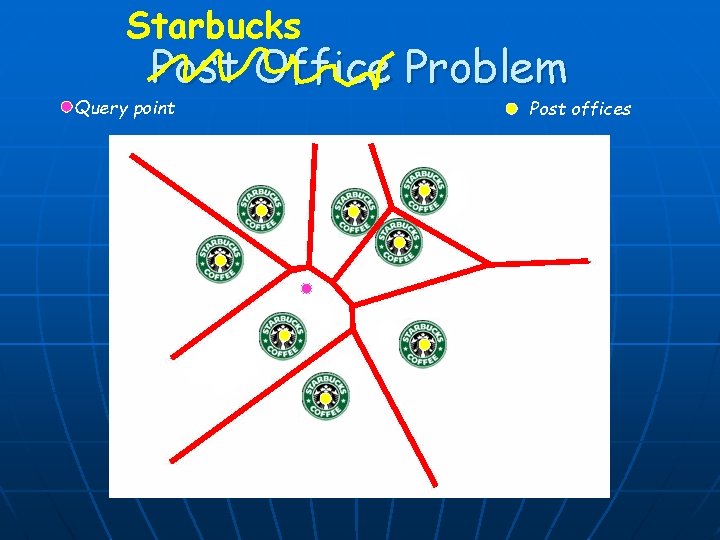
Starbucks Post Office Problem Query point Post offices

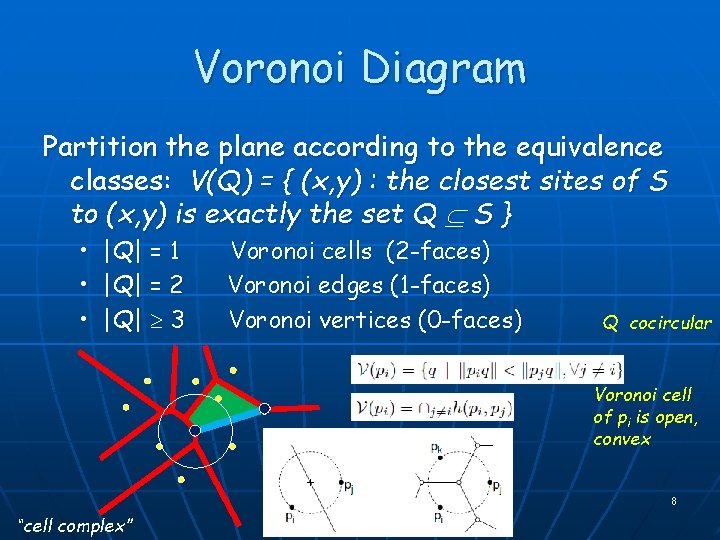
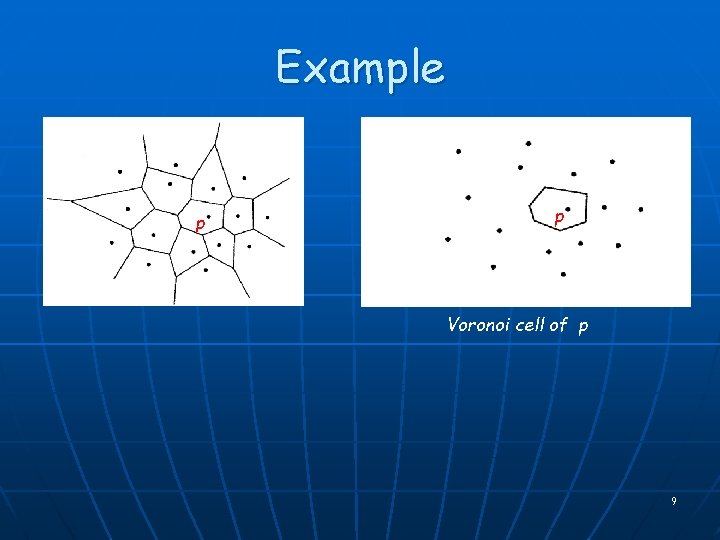
Voronoi Diagram Partition the plane according to the equivalence classes: V(Q) = { (x, y) : the closest sites of S to (x, y) is exactly the set Q S } • • • |Q| = 1 |Q| = 2 |Q| 3 Voronoi cells (2 -faces) Voronoi edges (1 -faces) Voronoi vertices (0 -faces) Q cocircular Voronoi cell of pi is open, convex 8 “cell complex”

Example p p Voronoi cell of p 9

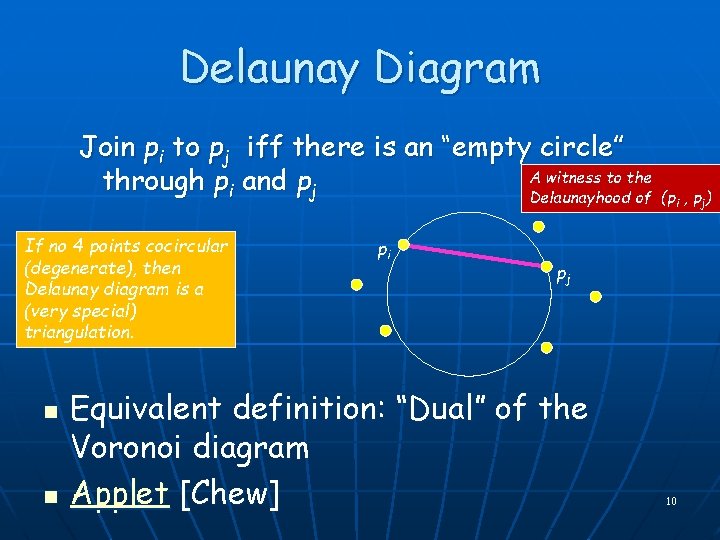
Delaunay Diagram Join pi to pj iff there is an “empty circle” A witness to the through pi and pj Delaunayhood of If no 4 points cocircular (degenerate), then Delaunay diagram is a (very special) triangulation. n n pi (pi , pj) pj Equivalent definition: “Dual” of the Voronoi diagram Applet [Chew] 10

Voronoi/Delaunay 11

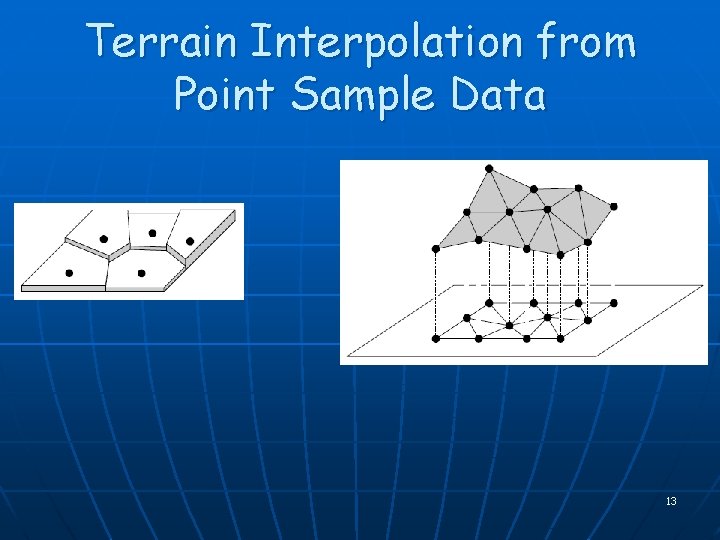
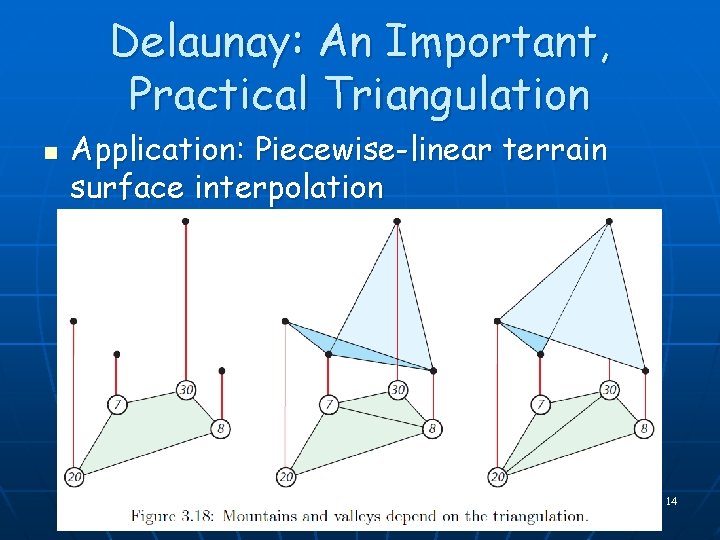
Delaunay: An Important, Practical Triangulation n Application: Piecewise-linear terrain surface interpolation 12

Terrain Interpolation from Point Sample Data 13

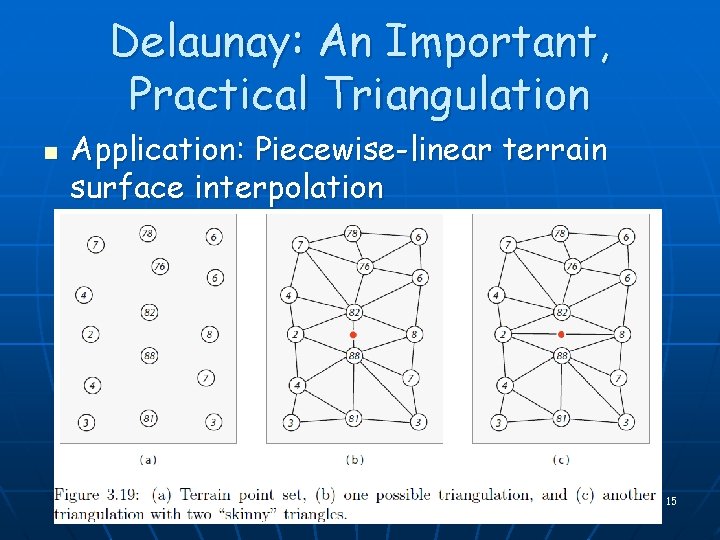
Delaunay: An Important, Practical Triangulation n Application: Piecewise-linear terrain surface interpolation 14

Delaunay: An Important, Practical Triangulation n Application: Piecewise-linear terrain surface interpolation 15

Delaunay for Terrain Interpolation 16

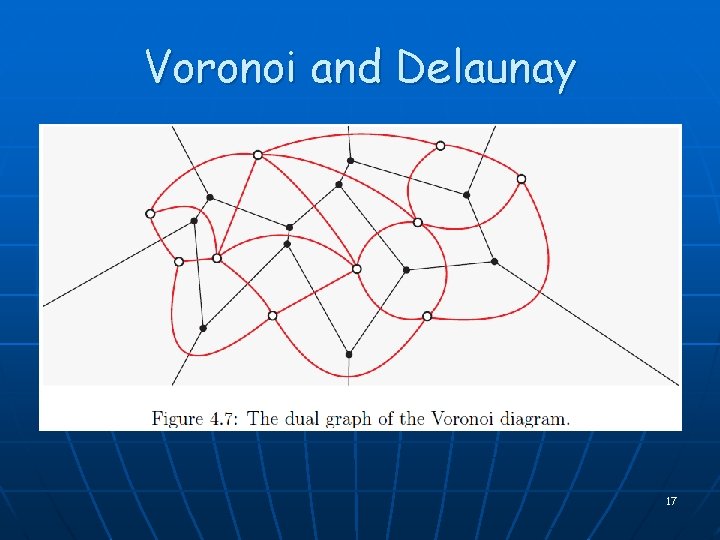
Voronoi and Delaunay 17

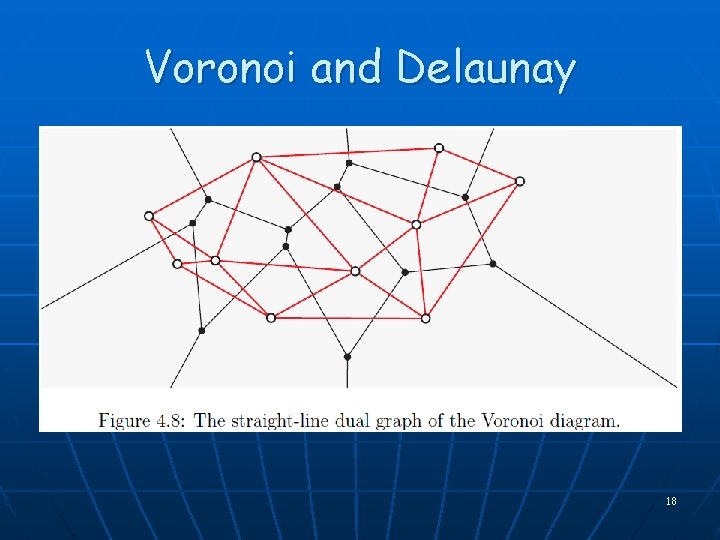
Voronoi and Delaunay 18

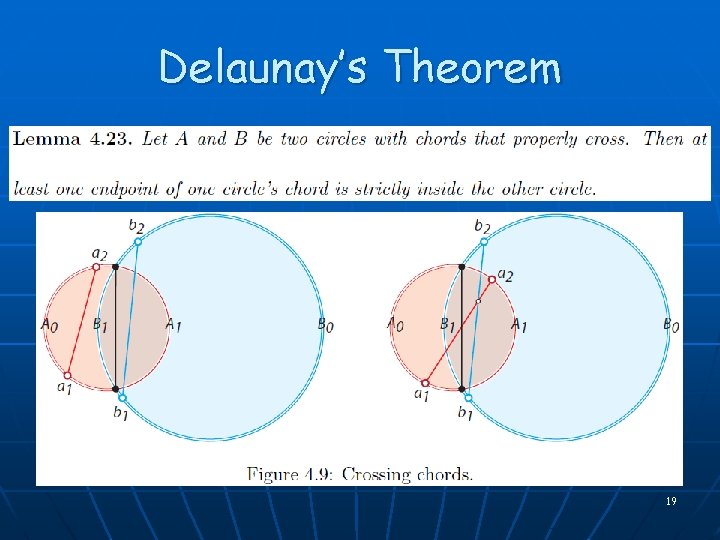
Delaunay’s Theorem 19

Delaunay’s Theorem 20

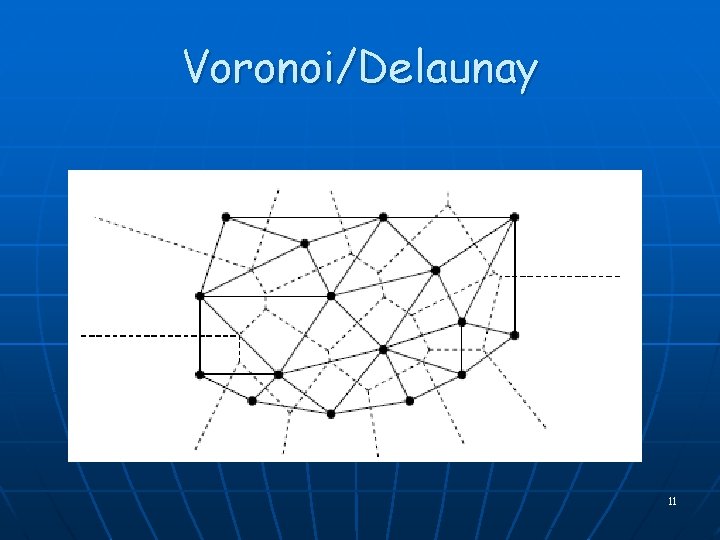
Voronoi and Delaunay Properties n n n The planar dual of Voronoi, drawn with nodes at the sites, edges straight segments, has no crossing edges [Delaunay]. It is the Delaunay diagram, D(S) (defined by empty circle property). Combinatorial size: 3 n-6 Voronoi/Delaunay edges; 2 n-5 Voronoi vertices (Delaunay faces) O(n) A Voronoi cell is unbounded iff its site is on the boundary of CH(S) = boundary of unbounded face of D(S) Delaunay triangulation lexico-maximizes the angle vector among all triangulations • In particular, maximizes the min angle 21

22

Angle Sequence of a Triangulation 23

Angle Sequence of a Triangulation 24

Legal Edges, Triangulations 25

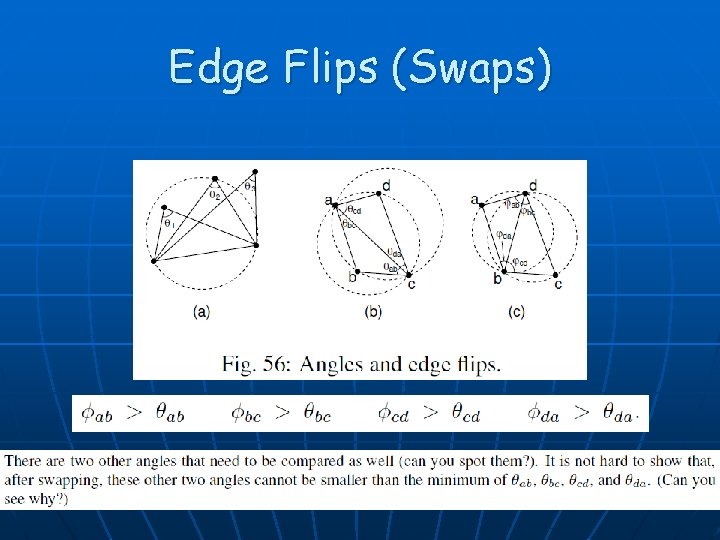
Edge Flips (Swaps) 26

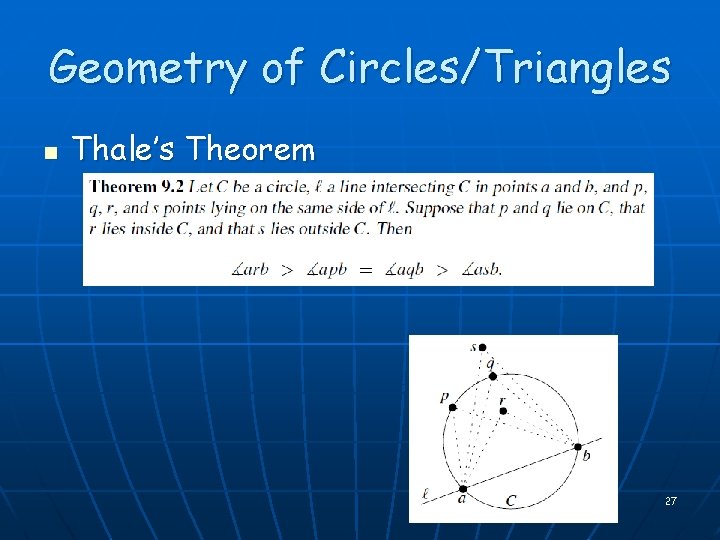
Geometry of Circles/Triangles n Thale’s Theorem 27

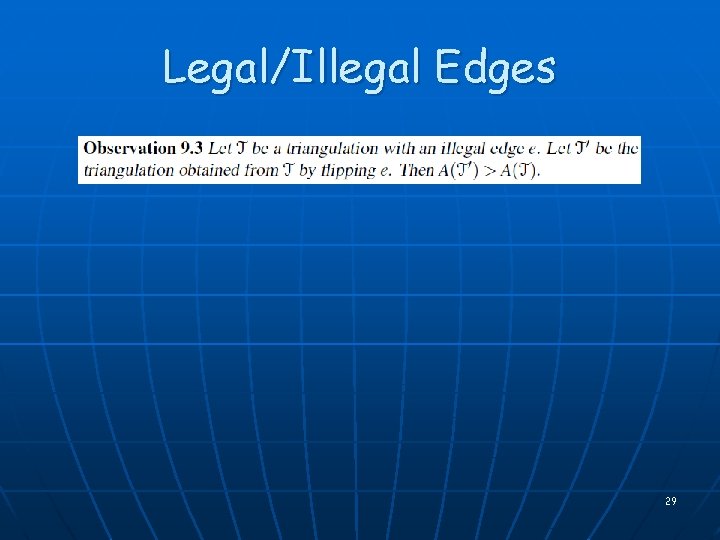
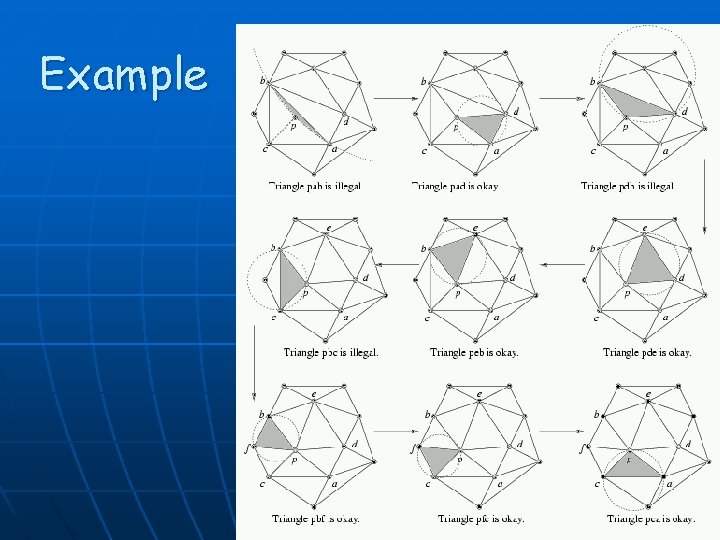
Legal/Illegal Edges Equivalent: • alpha 2 + alpha 6 > pi • In. Circle(pi , pk , pj , pl ) 28

Legal/Illegal Edges 29

Algorithm: Legalize Triangulation 30

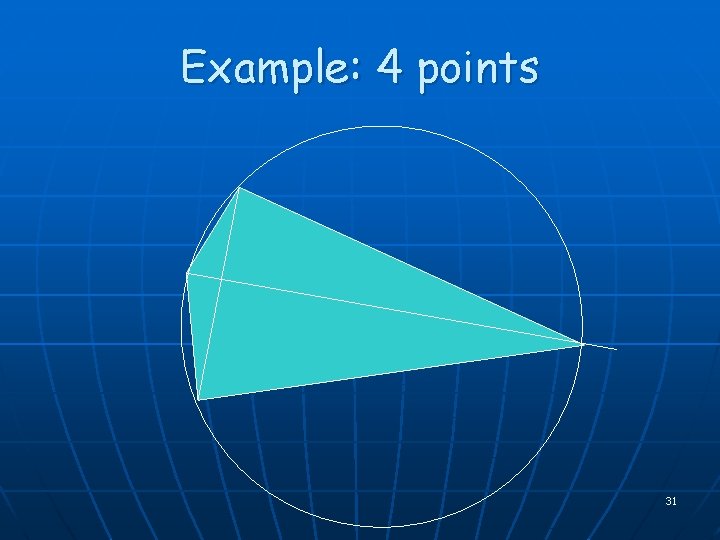
Example: 4 points 31

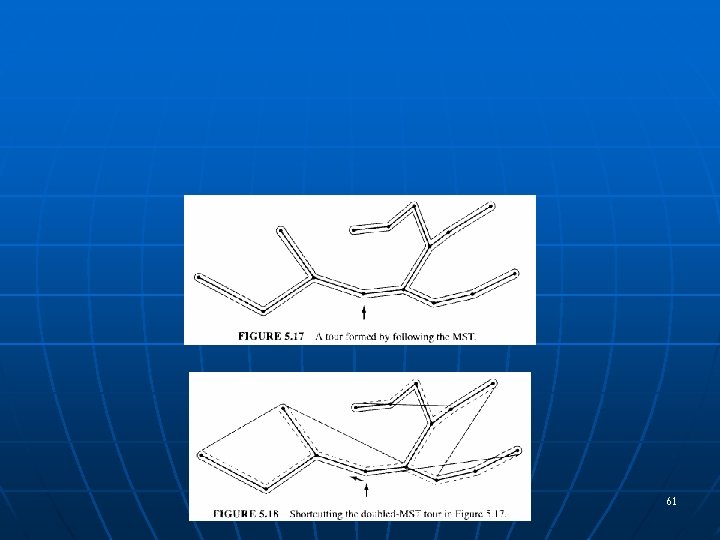
Voronoi and Delaunay Properties n n In any partition of S, S=B R, into blue/red points, any blue-red pair that is shortest B-R bridge is a Delaunay edge. Corollaries: • • • D(S) is connected MST D(S) (MST=“min spanning tree”) NNG D(S) (NNG=“nearest neighbor graph”) 32

Voronoi and Delaunay Properties n In any partition of S, S=B R, into blue/red points, any blue-red pair that is shortest B-R bridge is a Delaunay edge. • • • n Voronoi/Delaunay can be built in time O(n log n) • • • n D(S) is connected MST D(S) (MST=“min spanning tree”) NNG D(S) (NNG=“nearest neighbor graph”) Divide and conquer Sweep Randomized incremental Voro. Glide applet 33

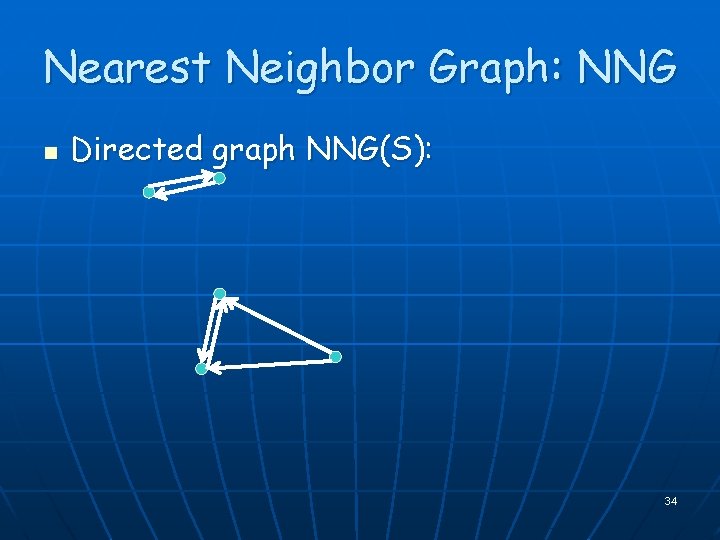
Nearest Neighbor Graph: NNG n Directed graph NNG(S): 34

Minimum Spanning Tree; MST n Greedy algorithms: • Prim: grows a tree • Kruskal: grows a forest: O(e log v) 35

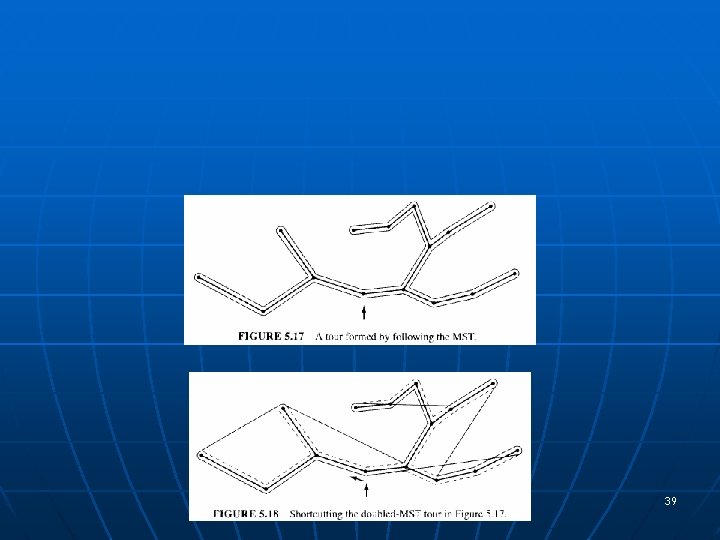
Euclidean MST n n One way to compute: Apply Prim or Kruskal to the complete graph, with edges weighted by their Euclidean lengths: O(n 2 log n) Better: Exploit the fact that MST is a subgraph of the Delaunay (which has size O(n)): • Apply Prim/Kruskal to the Delaunay: log n), since e = O(n) O(n 36

Euclidean MST 37

Traveling Salesperson Problem: TSP

39

Approximation Algorithms

PTAS for Geometric TSP

Voronoi Applet n Voro. Glide applet 42

Voronoi and Delaunay: 1 D Easy: Just sort the sites along the line Delaunay is a path Voronoi is a partition of the line into intervals Time: O(n log n) Lower bound: (n log n), since the Delaunay gives the sorted order of the input points, {x 1 , x 2 , x 3 , …} 43

Voronoi and Delaunay: 2 D Algorithms n n n n Naïve O(n 2 log n) algorithm: Build Voronoi cells one by one, solving n halfplane intersection problems (each in O(n log n), using divide-and-conquer) Incremental: worst-case O(n 2) Divide and conquer (first O(n log n)) Lawson Edge Swap (“Legalize”): Delaunay Randomized Incremental (expected O(n log n)) Sweep [Fortune] Any algorithm that computes CH in R 3 , e. g. , QHull Qhull website 44

45

Delaunay: Edge Flip Algorithm Lawson Edge Swap “Legalize” [BKOS] n n n Assume: No 4 co-circular points, for simplicity. d Start with any triangulation Keep a list (stack) of “illegal” edges: • • n n ab is illegal if In. Circle(a, c, b, d) Locally non-Delauany iff the smallest of the 6 angles goes up if flip b a c Flip any illegal edge; update legality status of neighboring edges Continue until no illegal edges Theorem: A triangulation is Delaunay iff there are no illegal edges (i. e. , it is “locally Delaunay”) Only O(n 2 ) flips needed. 46

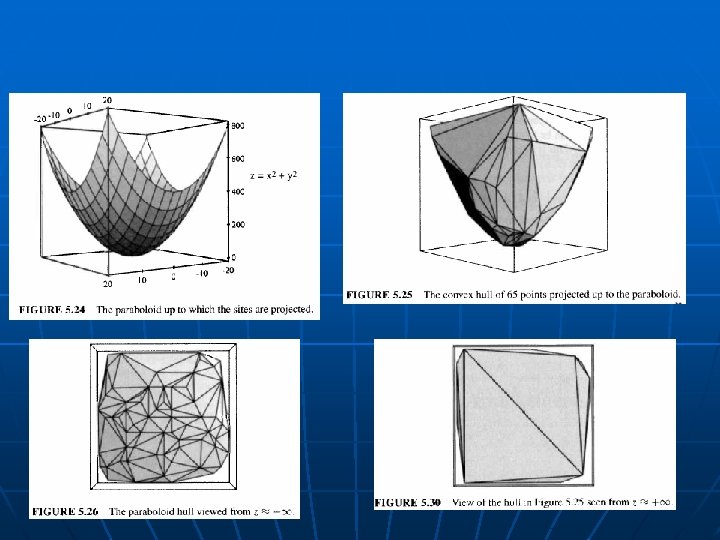
Connection to Convex Hulls in 3 D n n n Delaunay diagram lower convex hull of the lifted sites, (xi , yi , xi 2 +yi 2 ), on the paraboloid of revolution, z=x 2 + y 2 Upper hull “furthest site Delaunay” 3 D CH applet 47

48

49

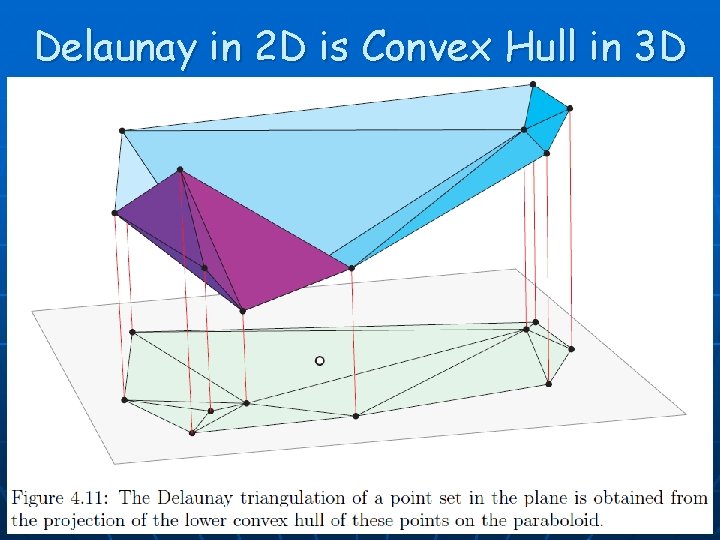
Delaunay in 2 D is Convex Hull in 3 D 50

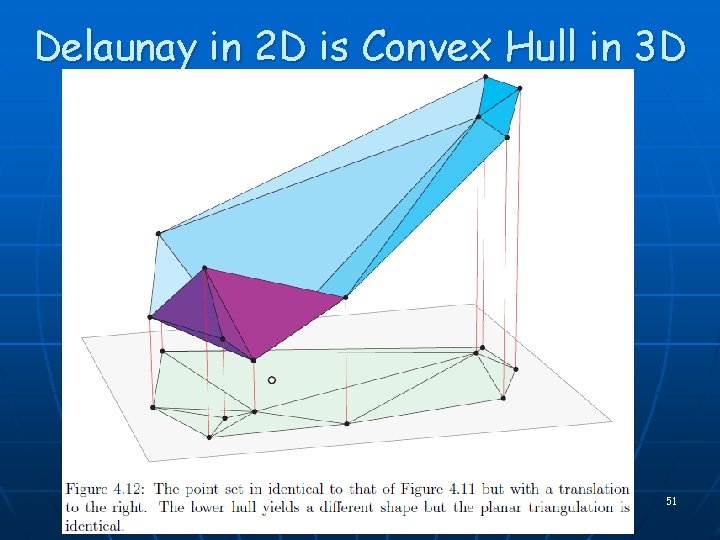
Delaunay in 2 D is Convex Hull in 3 D 51

Voronoi and Delaunay n Algorithms: • • • Straightforward incremental: O(n 2 ) Divide and conquer (first O(n log n)) Sweep Randomized incremental Any algorithm that computes CH in R 3 , e. g. , Qhull website QHull 52

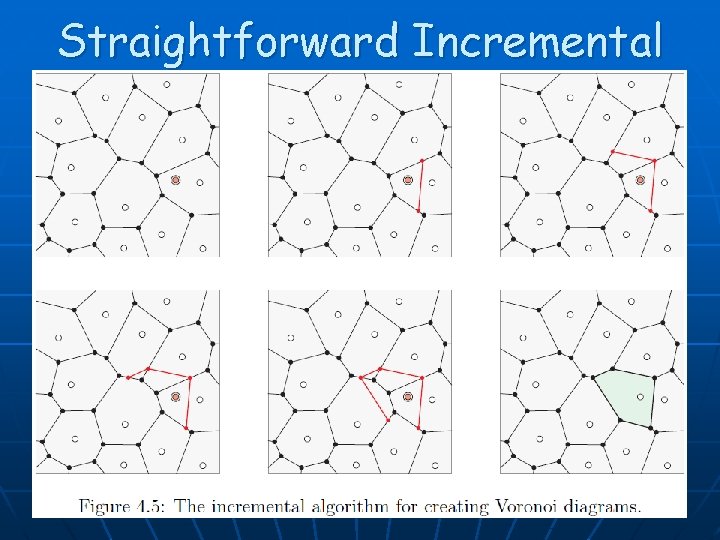
Straightforward Incremental Algorithm: Voronoi 53

Straightforward Incremental Algorithm: Voronoi 54

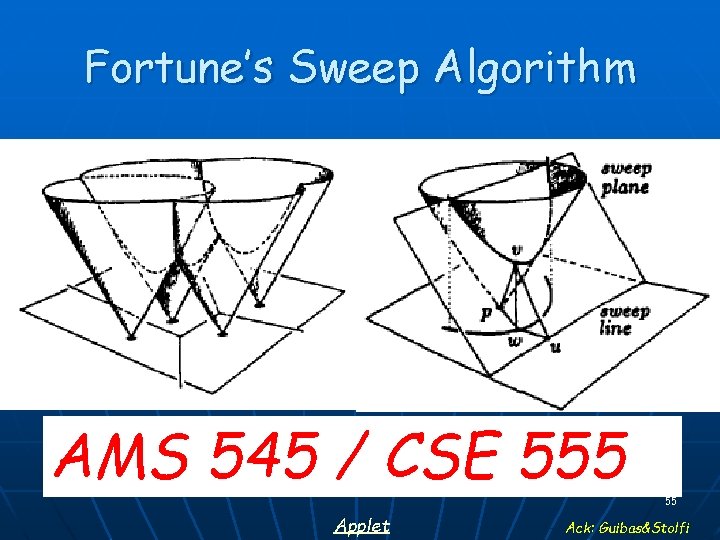
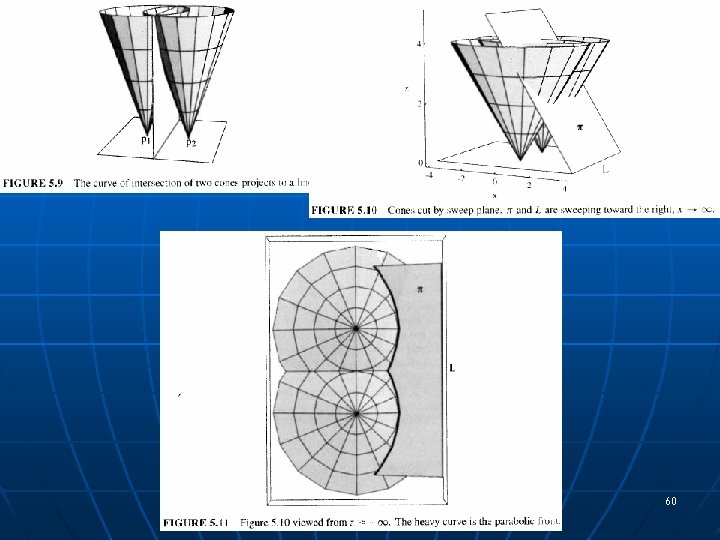
Fortune’s Sweep Algorithm AMS 545 / CSE 555 Applet 55 Ack: Guibas&Stolfi

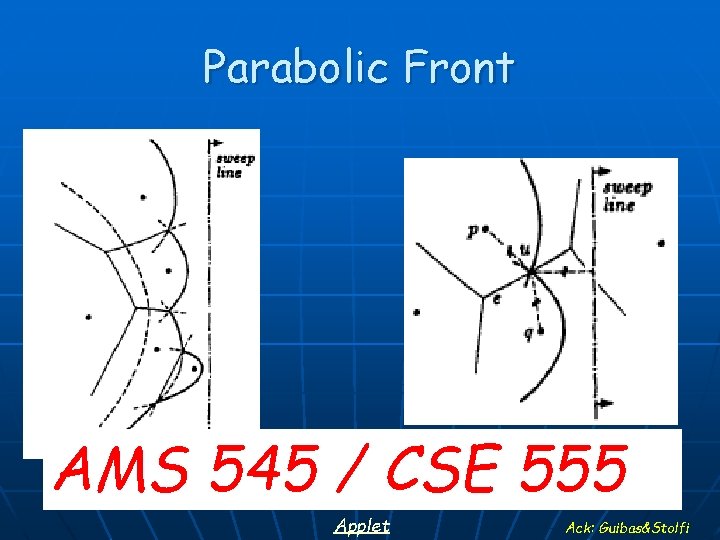
Parabolic Front AMS 545 / CSE 555 Applet 56 Ack: Guibas&Stolfi

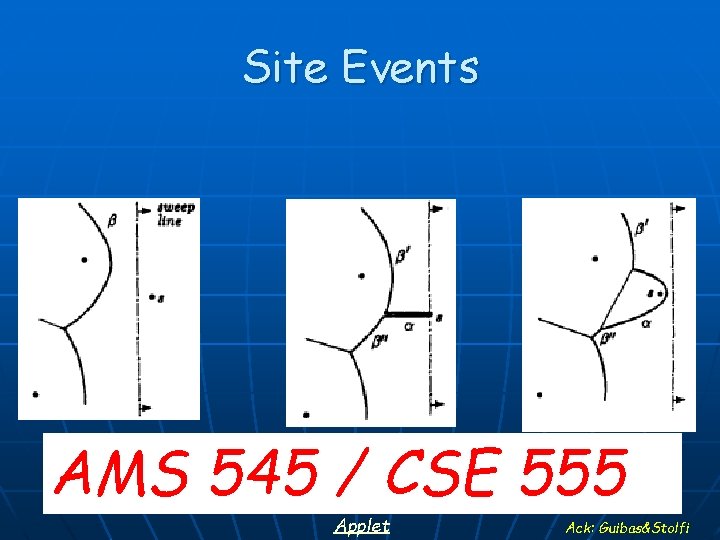
Site Events a) b) c) AMS 545 / CSE 555 Applet 57 Ack: Guibas&Stolfi

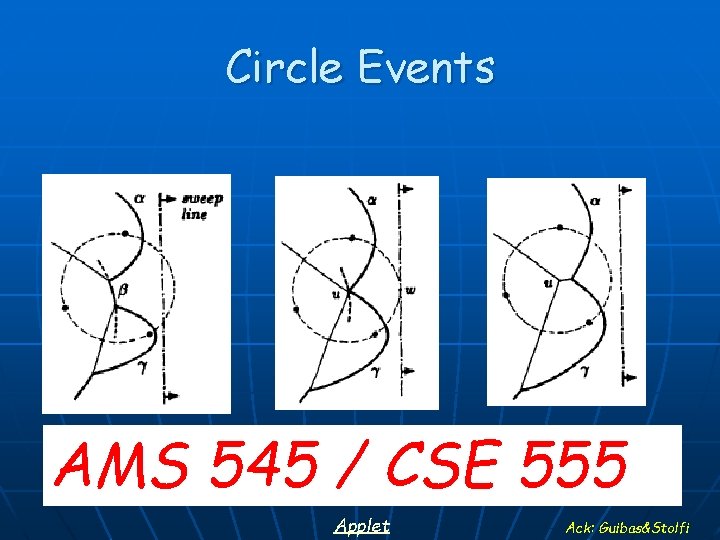
Circle Events AMS 545 / CSE 555 Applet 58 Ack: Guibas&Stolfi

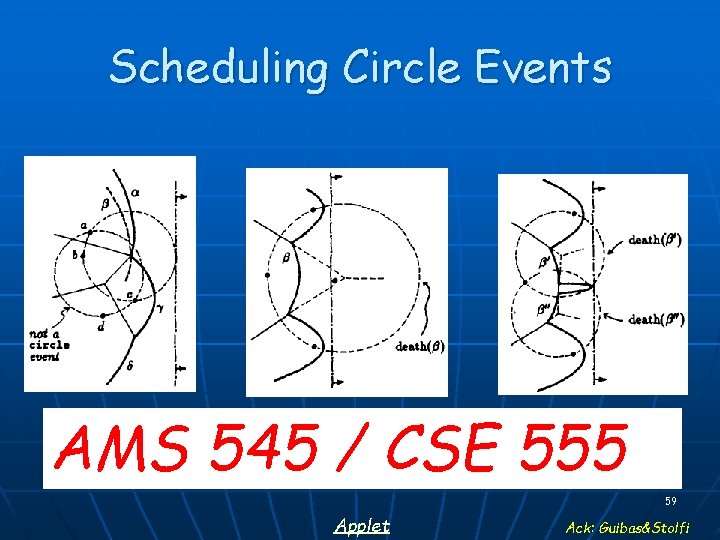
Scheduling Circle Events AMS 545 / CSE 555 59 Applet Ack: Guibas&Stolfi

60

61

Incremental Construction n Add sites one by one, modifying the Delaunay (Voronoi) as we go: • Join vi to 3 corners of triangle containing it • Do edge flips to restore local Delaunayhood n If added in random order, simple “Backwards analysis” shows expected time O(n log n) [Guibas, Knuth, Sharir] AMS 545 / CSE 555 62

Example CS 691 G Computational Geometry - UMass Amherst 63

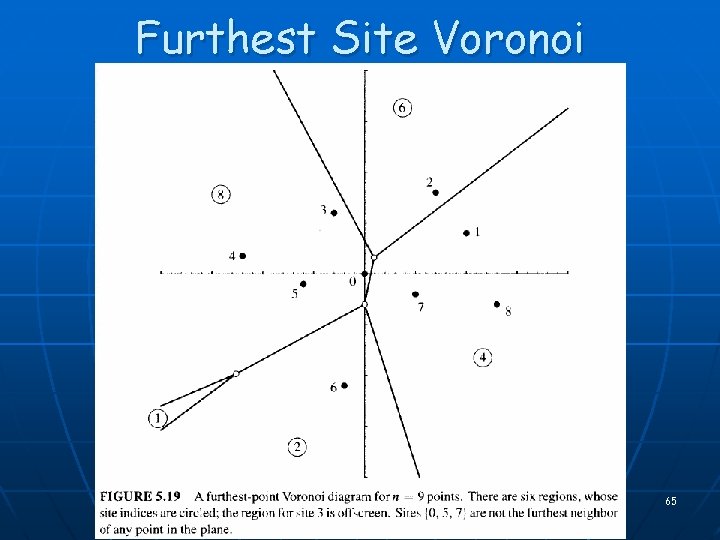
Voronoi Extensions n n n Numerous ! [see Okabe, Boots, Sugihara, Chiu] Different metrics Higher dimensions: • Delaunay in Rd lower CH in Rd+1 • O( n log n + n (d+1)/2 ) n n Order-k, furthest-site Other sites: Voronoi of polygons, “medial axis” Additive/multiplicative weights; power diagram -shapes: a powerful shape representation 64 Geo. Magic, biogeometry at Duke

Furthest Site Voronoi 65

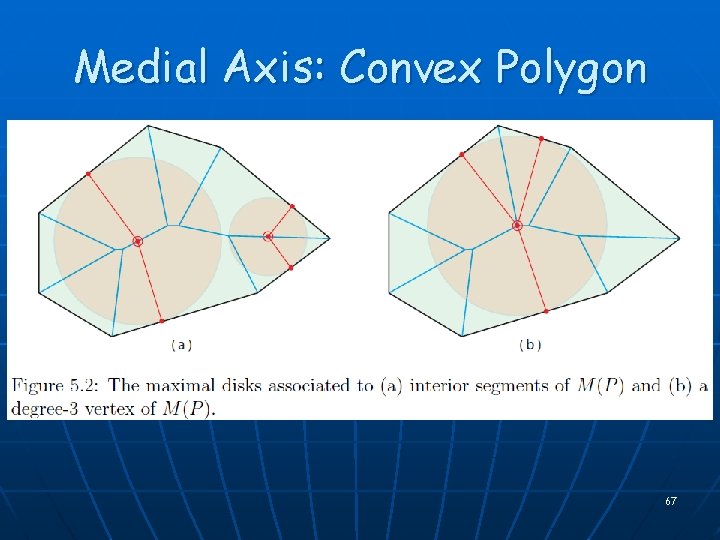
Medial Axis: Convex Polygon 66

Medial Axis: Convex Polygon 67

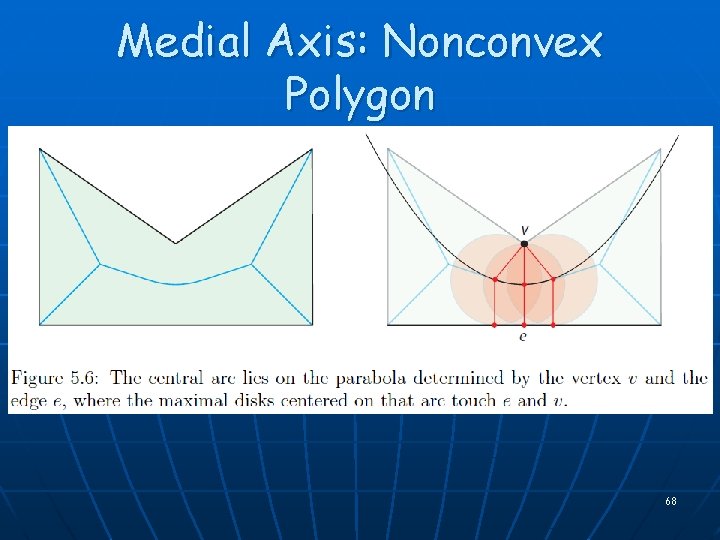
Medial Axis: Nonconvex Polygon 68

Medial Axis: Curved Domain 69

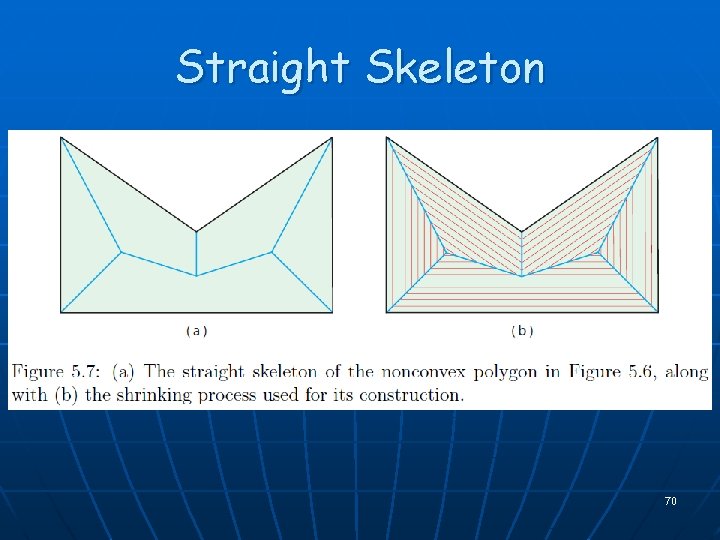
Straight Skeleton 70

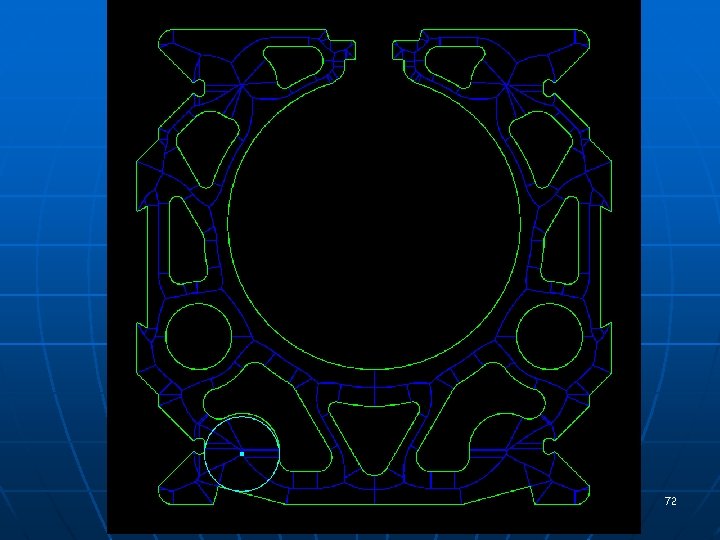
VRONI: Fast, robust Voronoi of polygonal domains Incremental algorithm 71

72

Computing offsets with a Voronoi diagram 73

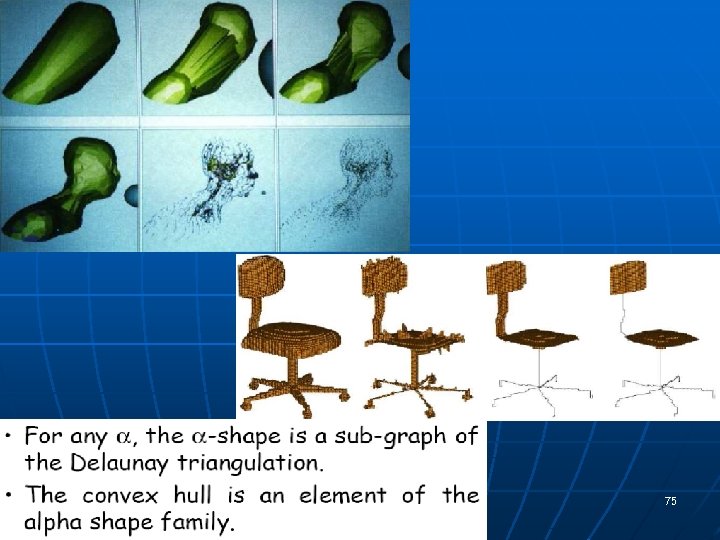
Alpha Shapes, Hulls “Erase” with a ball of radius to get -shape. Straighten edges to get -hull 74

75

-Shapes n n Theorem: For each Delaunay edge, e=(pi, pj), there exists min(e)>0 and max(e)>0 such that e -shape of S iff min(e) max(e). Thus, every alpha-hull edge is in the Delaunay, and every Delaunay edge is in some alpha-shape. Applet