Computational Geometry Piyush Kumar Lecture 10 Delaunay Triangulations

Computational Geometry Piyush Kumar (Lecture 10: Delaunay Triangulations and Voronoi Diagrams) Welcome to CIS 5930

Reading J. R. Shewchuk : Lecture notes on Delaunay Mesh Generation 2. 1 David Mount’s Lecture notes.

Triangulation of a vertex set V is a set of triangles whose vertices collectively are V, whose interiors do not intersect, and whose union is the convex hull of V. There are exponentially many different triangulations of V. A delaunay triangulation of a vertex set is the triangulation of V …

Delaunay Triangulations One special triangulation out of the exponentially many possible. (in some sense an optimal triangulation, we will come to that soon).

Voronoi Diagrams Recap: The post office problem

In the next two lectures We will study Delaunay triangulations and voronoi diagrams in more detail. Why study these diagrams? § They are the most used structures of computational geometry in other fields. o (GIS, Graphics, Vision, ML, Auto Industry, networks, scientific computing, hpc, …) § The most used structure in CG.

Delaunay Triangulation is a triangulation whose every edge is delaunay. What is a delaunay edge?

Delaunay Triangulations An edge (u, v) is called delaunay iff there exist an empty circumcircle passing thru (u, v). A circumcircle of the edge (u, v) is defined as any circle that passes thru (u, v)

Delaunay Triangulation Definition: A Delaunay triangulation is a set of triangles T in which each edge of T possesses at least one empty circumcircle. Empty: A circumcircle is said to be empty if it contains no nodes of the set V

Delaunay Triangulation Assuming no d+1 points are cocircular/cospherical, the set of all delaunay edges partition the convex hull and form the delaunay triangulation. Proof: Non-Trivial, but easy with the lemmas we prove today. (See Shewchuk notes, Page 15)

Delaunay Triangulations Lemma 1: Every edge on the convex hull is delaunay.

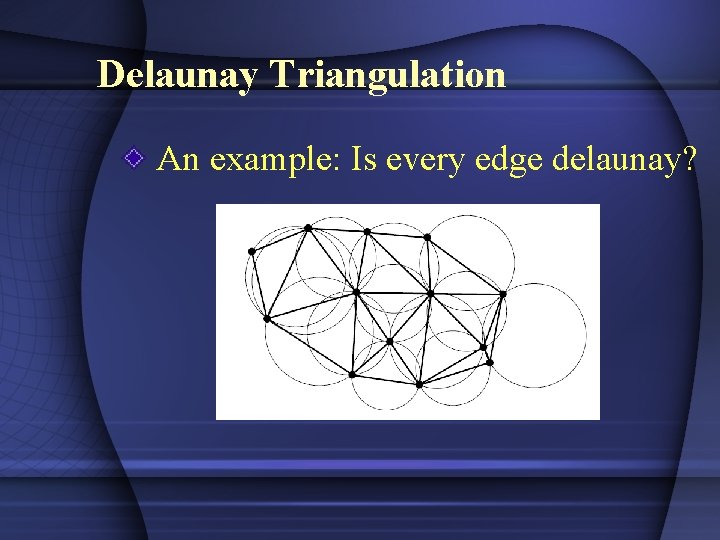
Delaunay Triangulation An example: Is every edge delaunay?

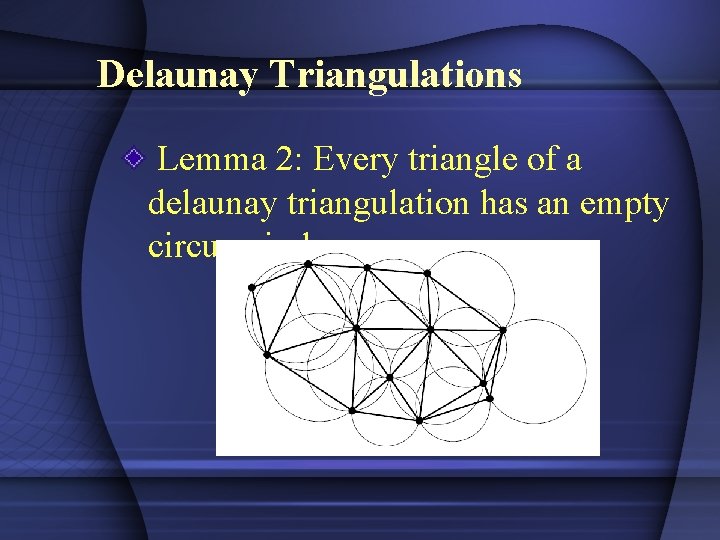
Delaunay Triangulations Lemma 2: Every triangle of a delaunay triangulation has an empty circumcircle.

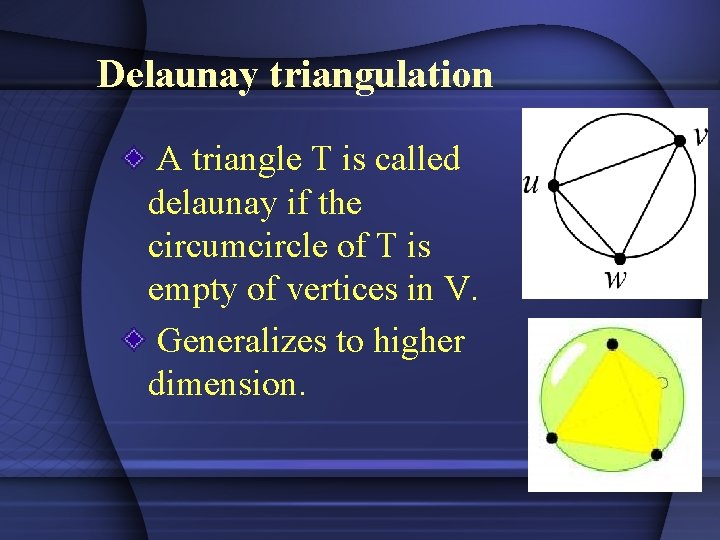
Delaunay triangulation A triangle T is called delaunay if the circumcircle of T is empty of vertices in V. Generalizes to higher dimension.

Delaunay Triangulation Lemma 3: Every edge connecting a vertex to its nearest neighbor is delaunay. Proof?

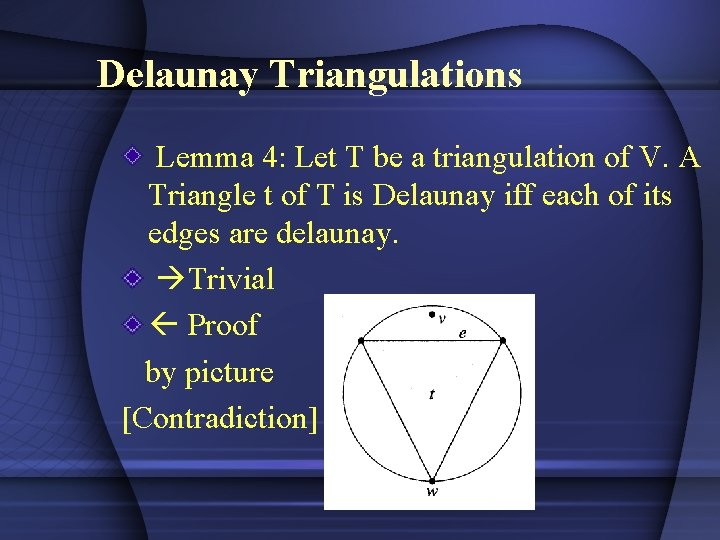
Delaunay Triangulations Lemma 4: Let T be a triangulation of V. A Triangle t of T is Delaunay iff each of its edges are delaunay. Trivial Proof by picture [Contradiction]

Delaunay Triangulations Lemme 4: Restated Let T be a triangulation. If all the triangles of T are delaunay, then all the edges of T are delaunay, and vice versa.

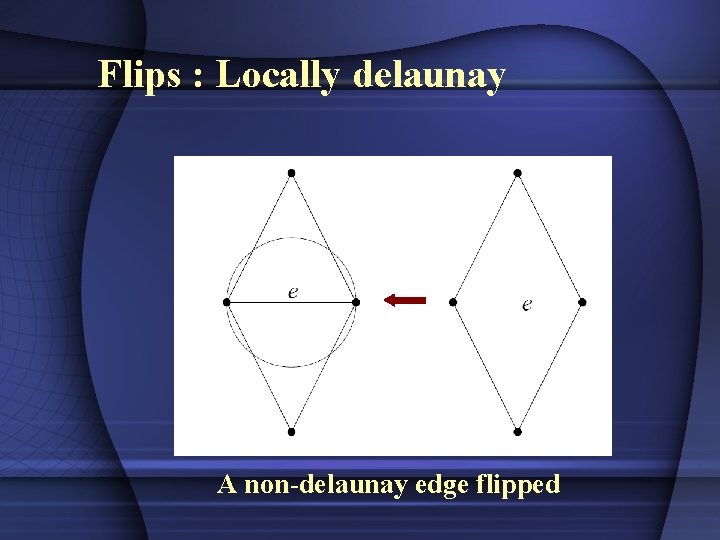
Lemma 5 Let e be an edge of a triangulation of V. Either e is locally delaunay, or e is flippable and the edge created by flipping e is locally delaunay.

Flips : Locally delaunay A non-delaunay edge flipped

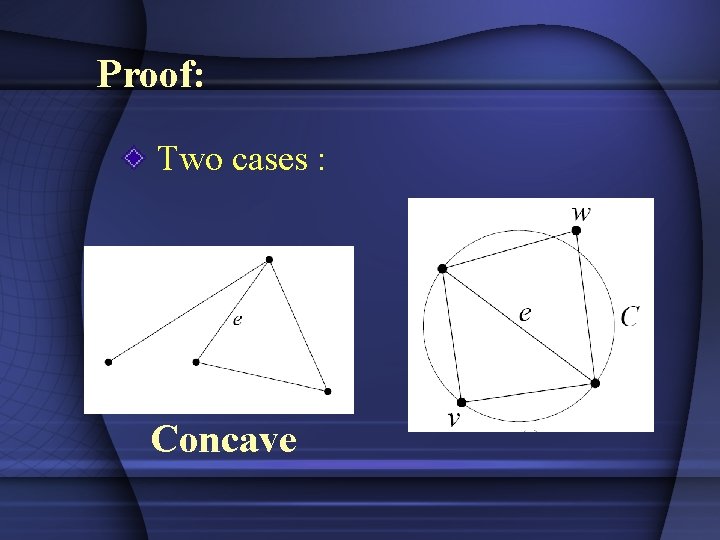
Proof: Two cases : Concave

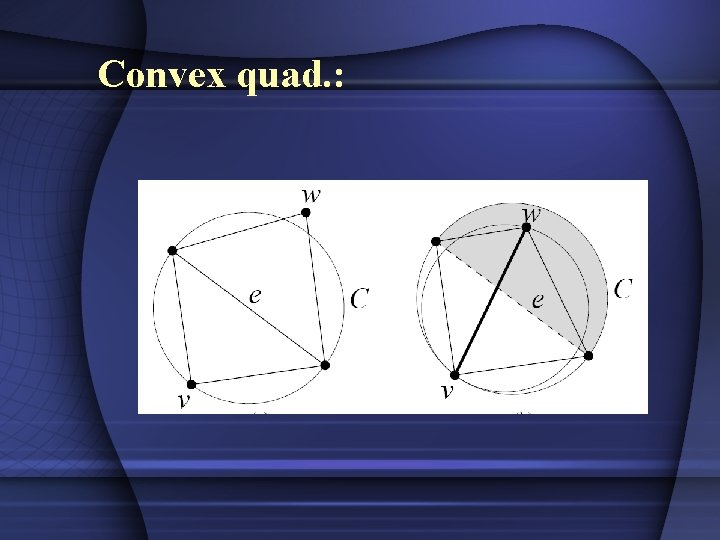
Convex quad. :

Flip Algorithm 1. Let V be the set of input vertices. 2. T = Any Triangulation of V. 3. Repeat unitil all edges of T are delaunay edges. 1. Find a non-delaunay edge that is flippable. o Flip

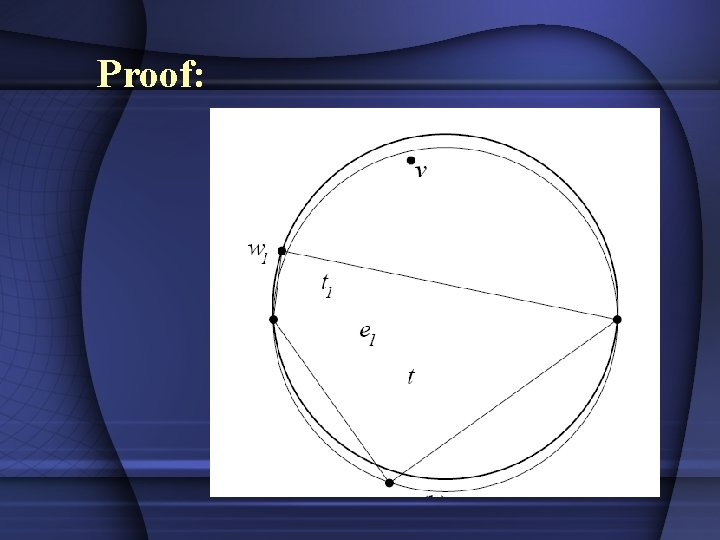
Locally Delaunay Globally delaunay If T is a triangulation with all its edges locally delaunay, then T is the delaunay triangulation. Proof by contradiction: § Let all edges of T be locally delaunay but an edge of T is not delaunay. By lemma 4, there must be a triangle in T which is nondelaunay.

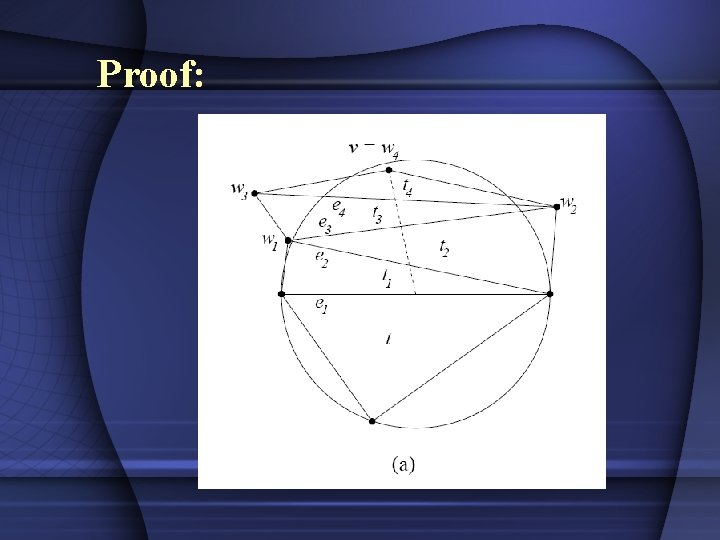
Proof:

Proof:

Corollary If a triangulation contains an edge that is not delaunay, it also contains an edge that is not locally delaunay. And hence the flip algorithm terminates.

Flip Algorithm: How many flips? The flip algorithm terminates after at most O(n 2) flips. Why?

Flip Algorithm: How many flips? Let <T> be a function defined over all triangulations § <T> = Number of vertex triangle pairs (v, t) such that v is vertex of T, t is triangle of T and circum-circle of t contains v. § <T> = O(n 2). Why? o Number of vertices = n o Number of triangles = O(n)

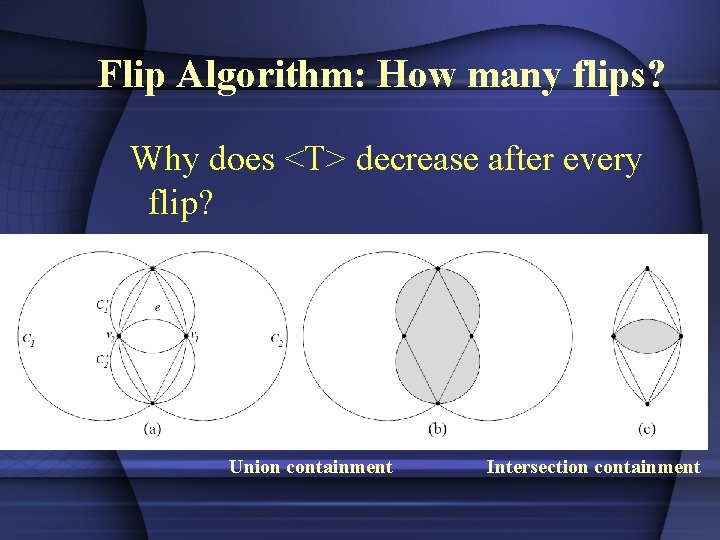
Flip Algorithm: How many flips? Claim : <T> decreases by at least 2 after evey flip. Hence, in total there can be no more than O(n 2) flips. Why does <T> decrease after every flip?

Flip Algorithm: How many flips? Why does <T> decrease after every flip? Union containment Intersection containment

Flip Algorithm 1. 2. 3. Let V be the set of input vertices. T = Any Triangulation of V. Repeat unitil all edges of T are delaunay edges. 1. Find a non-delaunay edge that is flippable. o Flip Trivial implementation O(n 3).

Properties Among all triangulations of a vertex set, delaunay triangulations maxime the minimum angle in the triangulation, minimize the largest circumcircle, minimize the largest MEB. Why? Each of these properties is locally improved on a flip.

Properties MST of the complete graph of a point set is subset of Delaunay triangulation If a smooth curve or surface has enough sample points on them, delaunay triangulation contains the reconstruction.

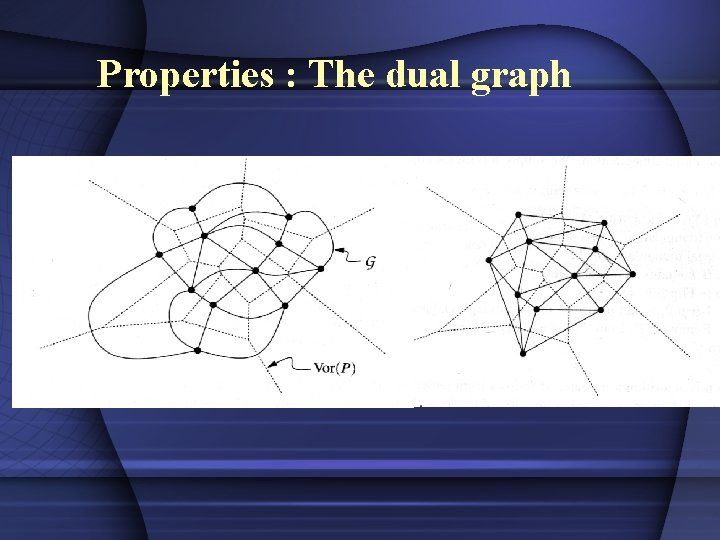
Properties : The dual graph

Better Algorithms? We can do Delaunay triangulations in O(nlogn) time ! § Incremental § Divide and Conquer § Sweepline Best Time complexity? § O(nlogn)

Randomized incremental Alg. On the chalkboard

Delaunay Triangulation How to compute in real life? The following libraries provide code to compute delaunay triangulations 1. Triangle (Jonathan) 2. Qhll (Brad) 3. CGAL and LEDA § o (projects started at MPI Saarbruecken)