Stress strain relationship for anisotropic materials Examples of






















![APPENDIX 2 Linear elasticity 1) The elements of matrix [S] are constant Non linear APPENDIX 2 Linear elasticity 1) The elements of matrix [S] are constant Non linear](https://slidetodoc.com/presentation_image_h2/7eb1a38dbf76898dd199862b9ee97c35/image-35.jpg)
- Slides: 35

Stress strain relationship for anisotropic materials

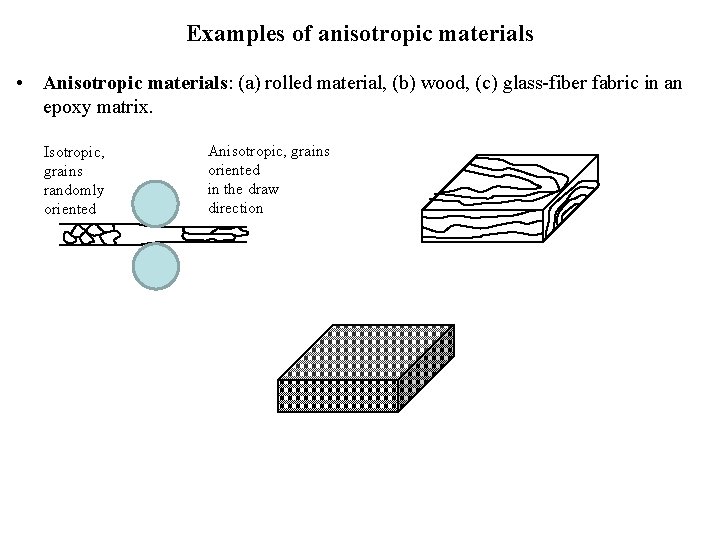
Examples of anisotropic materials • Anisotropic materials: (a) rolled material, (b) wood, (c) glass-fiber fabric in an epoxy matrix. Isotropic, grains randomly oriented Anisotropic, grains oriented in the draw direction

Isotropic and anisotropic • Isotropic material: the elastic behavior at small strains is fully characterized by 2 independent parameters, for example Young modulus E and shear modulus G. These parameters do not depend on the direction of the applied load. • Anisotropic material: The elastic behavior depends on the direction of the applied loads the design of a structure made with composite materials requires the knowledge of many elastic properties, in principle different for each direction of the applied load. • The elastic properties of an anisotropic body depend on a limited number of parameters (>2) associated with the nature of internal structure of the material. • The study of the elastic behavior of materials is aimed to: 1. Define the experiments needed to characterize the minimum number of elastic properties of a given material. 2. Correlate stress and strain fields for each direction of the applied loads

Isotropic and homogeneous • A material is isotropic when its mechanical properties remain the same in all the directions at a given point while they may change from point to point. • A material is homogeneous when its mechanical properties may be different along different directions at given point, but this variation is consistent from point to point. • For example, consider three common items on a dining table: stainless steel forks, bamboo chopsticks and swiss cheese. • Stainless steel is isotropic and homogeneous. • Bamboo chopsticks are homogeneous but not isotropic (they are transversely isotropic, strong along the fiber direction, relatively weak but equal in other directions). • Swiss cheese is isotropic but not homogeneous (the air bubbles formed during production left inhomogeneous spots).

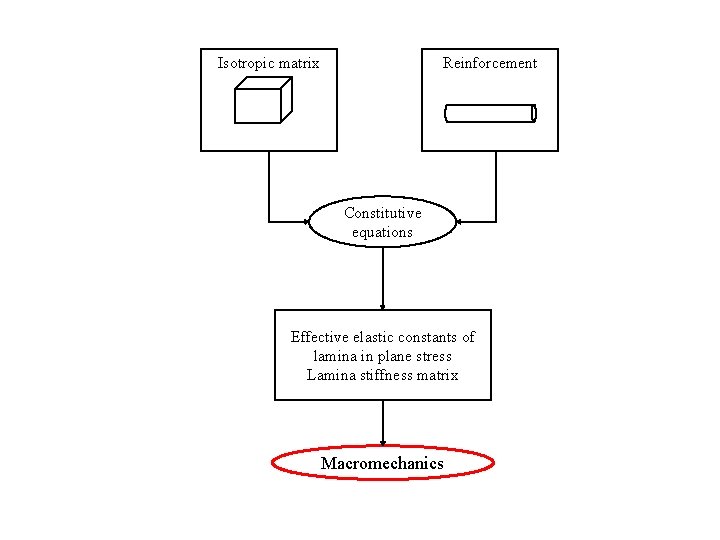
Isotropic matrix Reinforcement Constitutive equations Effective elastic constants of lamina in plane stress Lamina stiffness matrix Macromechanics

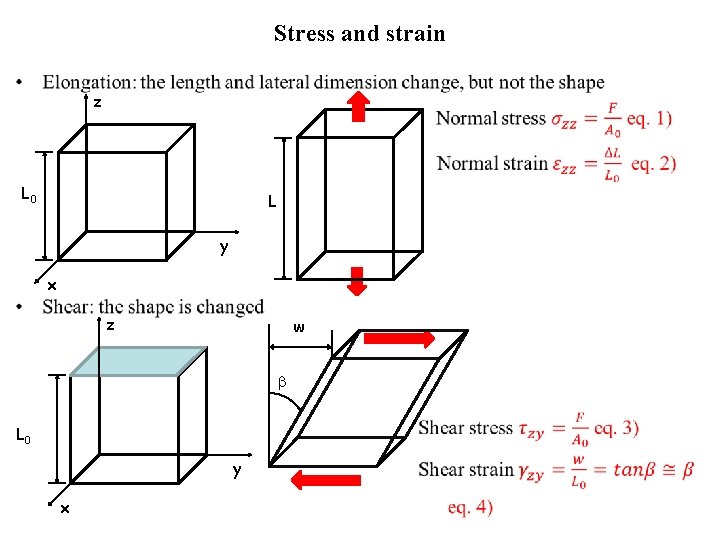
Stress and strain • z L 0 L y x z w L 0 y x

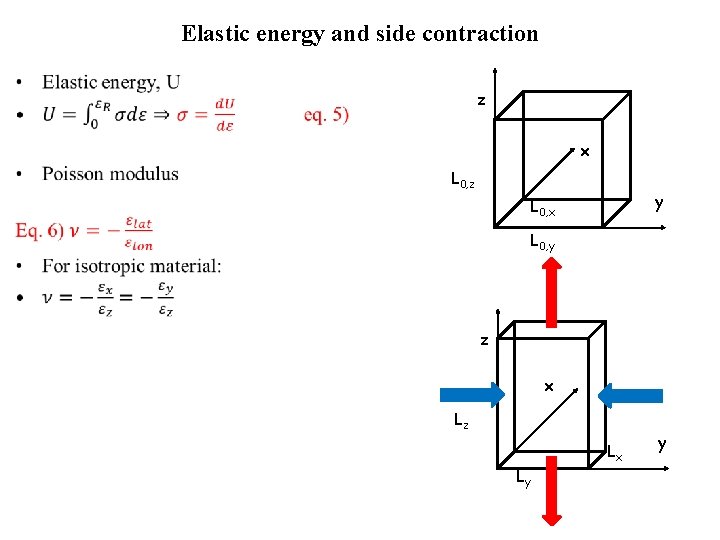
Elastic energy and side contraction • z x L 0, z y L 0, x L 0, y z x Lz Lx Ly y

Tensor •

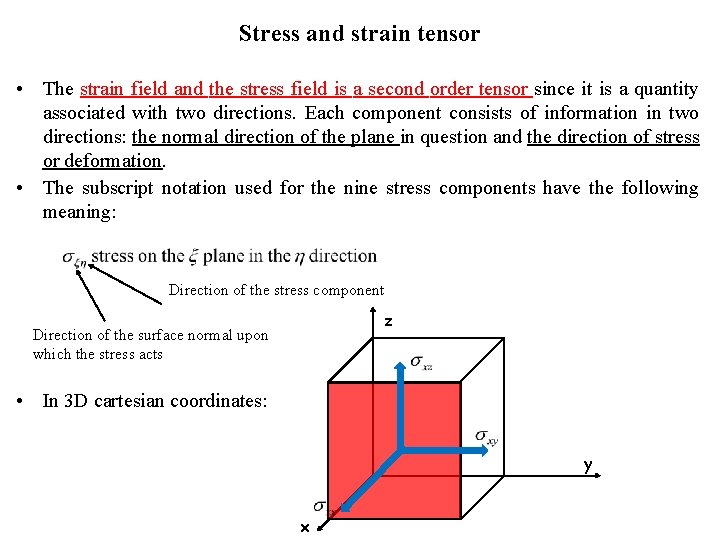
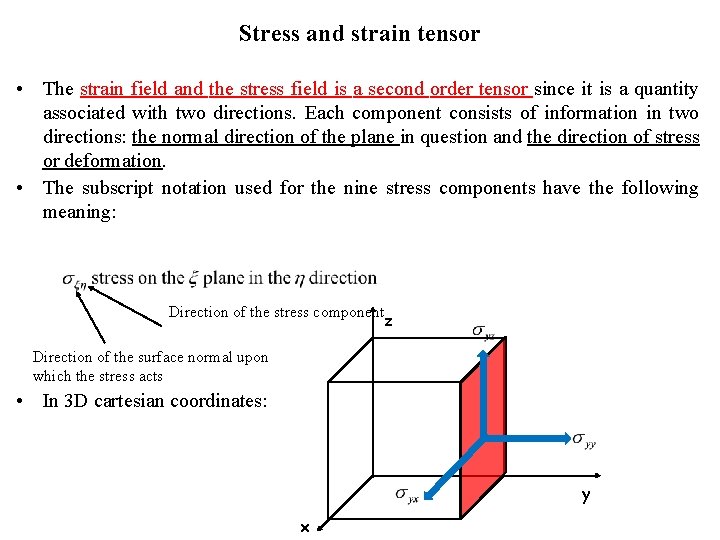
Stress and strain tensor • The strain field and the stress field is a second order tensor since it is a quantity associated with two directions. Each component consists of information in two directions: the normal direction of the plane in question and the direction of stress or deformation. • The subscript notation used for the nine stress components have the following meaning: Direction of the stress component z Direction of the surface normal upon which the stress acts • In 3 D cartesian coordinates: y x

Stress and strain tensor • The strain field and the stress field is a second order tensor since it is a quantity associated with two directions. Each component consists of information in two directions: the normal direction of the plane in question and the direction of stress or deformation. • The subscript notation used for the nine stress components have the following meaning: Direction of the stress component z Direction of the surface normal upon which the stress acts • In 3 D cartesian coordinates: y x

Stress and strain tensor • The strain field and the stress field is a second order tensor since it is a quantity associated with two directions. Each component consists of information in two directions: the normal direction of the plane in question and the direction of stress or deformation. • The subscript notation used for the nine stress components have the following meaning: Direction of the stress component z Direction of the surface normal upon which the stress acts • In 3 D cartesian coordinates: y x

Stress field • It is a II order tensor 9 components (i. e. a matrix) • Equilibrium to rotation, involving shear stresses, leads to a symmetry in the matrix 6 components Therefore, the most common way to represent the stress tensor is Or alternatively: Being 1=xx; 2=yy; 3=zz; 4=yz; 5=xz; 6=xy

Strain field •

Strain field •

Constitutive equations •

Generalized Hooke’s Law for Anisotropic Material •

Generalized Hooke’s Law for Anisotropic Material •

Symmetry of compliance matrix •

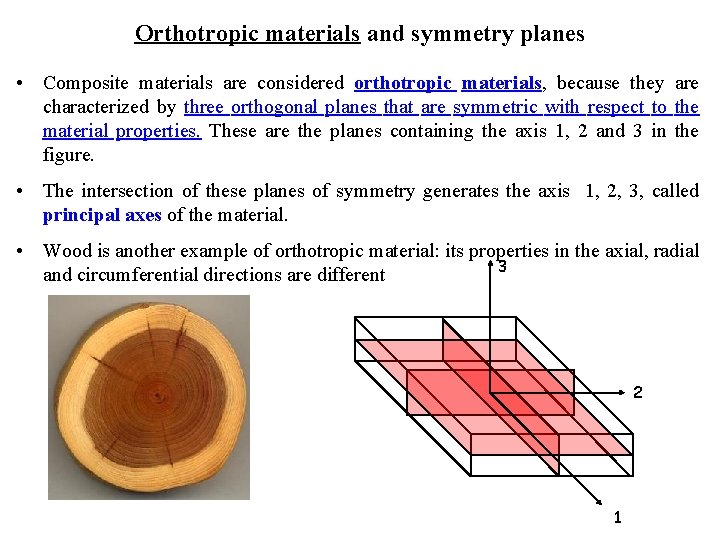
Orthotropic materials and symmetry planes • Composite materials are considered orthotropic materials, because they are characterized by three orthogonal planes that are symmetric with respect to the material properties. These are the planes containing the axis 1, 2 and 3 in the figure. • The intersection of these planes of symmetry generates the axis 1, 2, 3, called principal axes of the material. • Wood is another example of orthotropic material: its properties in the axial, radial 3 and circumferential directions are different 2 1

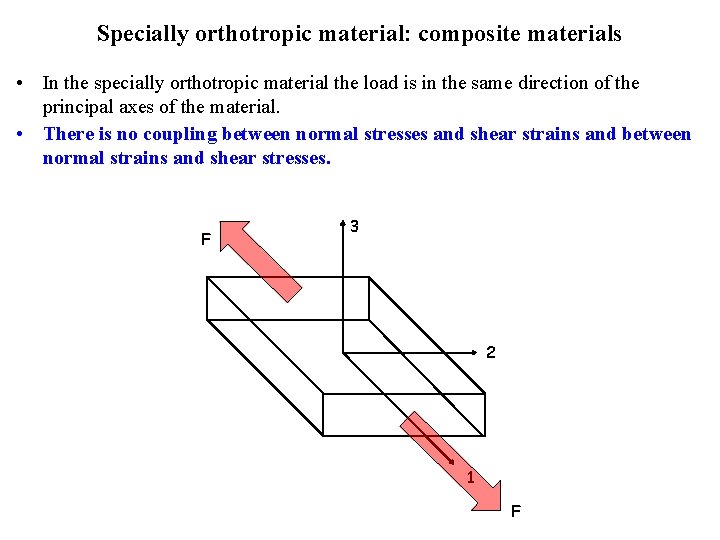
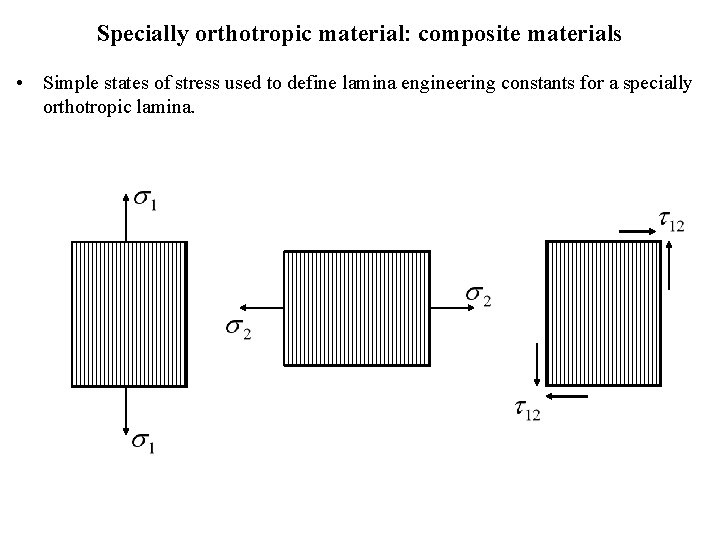
Specially orthotropic material: composite materials • In the specially orthotropic material the load is in the same direction of the principal axes of the material. • There is no coupling between normal stresses and shear strains and between normal strains and shear stresses. F 3 2 1 F

Specially orthotropic material: composite materials • Simple states of stress used to define lamina engineering constants for a specially orthotropic lamina.

Classes of materials • • • Anisotropic (triclinic) material: there are no planes of symmetry for the material properties; its properties depend on the direction in which they are measured. Monoclinic material: has 1 plane of symmetry. Orthotropic material: has 3 planes of symmetry so that its material properties are, in general, different along each axis. Specially orthotropic material: orthotropic material in which the load is in the same direction of the principal axes of the material. There is no interaction between normal stresses 1, 2, 3 and shear strains 4, 5, 6 such as occurs in anisotropic materials. Transversely isotropic material: is a special orthotropic materials that have one plane where the material is isotropic, i. e. there exists a plane in which the mechanical properties are equal in all directions. One common example of transversely isotropic material with one axis of symmetry is a polymer reinforced by unidirectional fibers. The strength and stiffness of such a composite material will usually be greater in a direction parallel to the fibers than in the transverse direction, and the thickness direction usually has properties similar to the transverse direction. Isotropic material: has an infinite number of planes of symmetry and has the same properties in each direction.

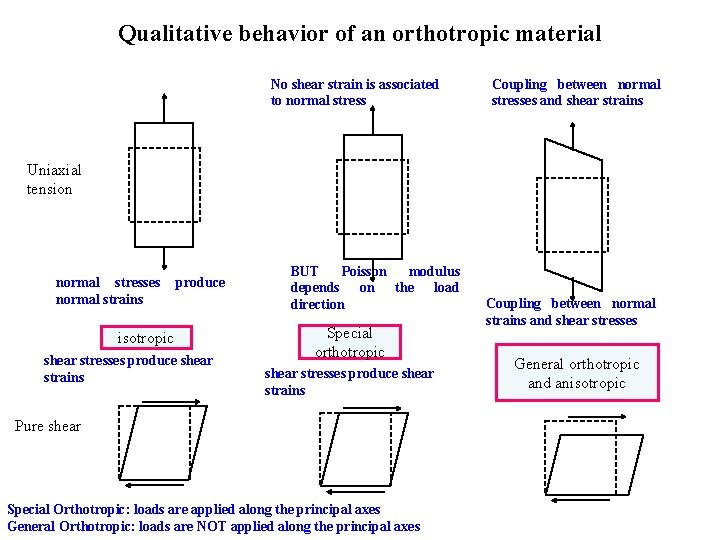
Qualitative behavior of an orthotropic material No shear strain is associated to normal stress Coupling between normal stresses and shear strains Uniaxial tension normal stresses normal strains produce isotropic shear stresses produce shear strains BUT Poisson modulus depends on the load direction Special orthotropic shear stresses produce shear strains Pure shear Special Orthotropic: loads are applied along the principal axes General Orthotropic: loads are NOT applied along the principal axes Coupling between normal strains and shear stresses General orthotropic and anisotropic

Specially orthotropic materials: elastic constants using as a reference axis the symmetry axis •

Specially orthotropic materials: elastic constants using as a reference axis the symmetry axis •

Specially orthotropic materials: elastic constants using as a reference axis the symmetry axis •

Specially orthotropic materials: symmetry of the compliance matrix •

Specially orthotropic materials: stiffness matrix •

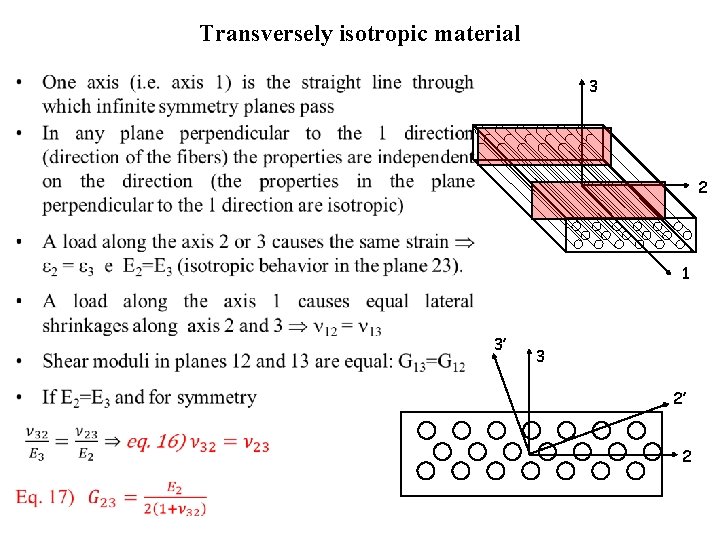
Transversely isotropic material • 3 2 1 3’ 3 2’ 2

Transversely isotropic material •

Isotropic materials: elastic constants •

Synthesis

Plane tension • z

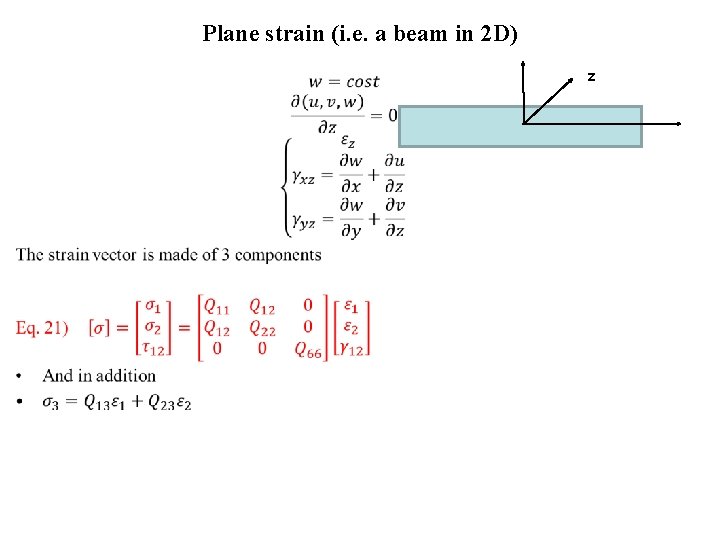
Plane strain (i. e. a beam in 2 D) • z
![APPENDIX 2 Linear elasticity 1 The elements of matrix S are constant Non linear APPENDIX 2 Linear elasticity 1) The elements of matrix [S] are constant Non linear](https://slidetodoc.com/presentation_image_h2/7eb1a38dbf76898dd199862b9ee97c35/image-35.jpg)
APPENDIX 2 Linear elasticity 1) The elements of matrix [S] are constant Non linear elasticity 2) The elements of the [S] matrix are not any more constant but they are a function of the stress (2) (1) - Linear elasticity can be modeled adopting relationship between vectors through matrices either for isotropic either for anisotropic materials -Numerical analysis of elasticity problems is not really complicated when an anisotropic material is used. -The inverse relationship is: where [C]= [S]-1 is called the stiffness matrix