Adversarial Search Adversarial Search Game playing Perfect play












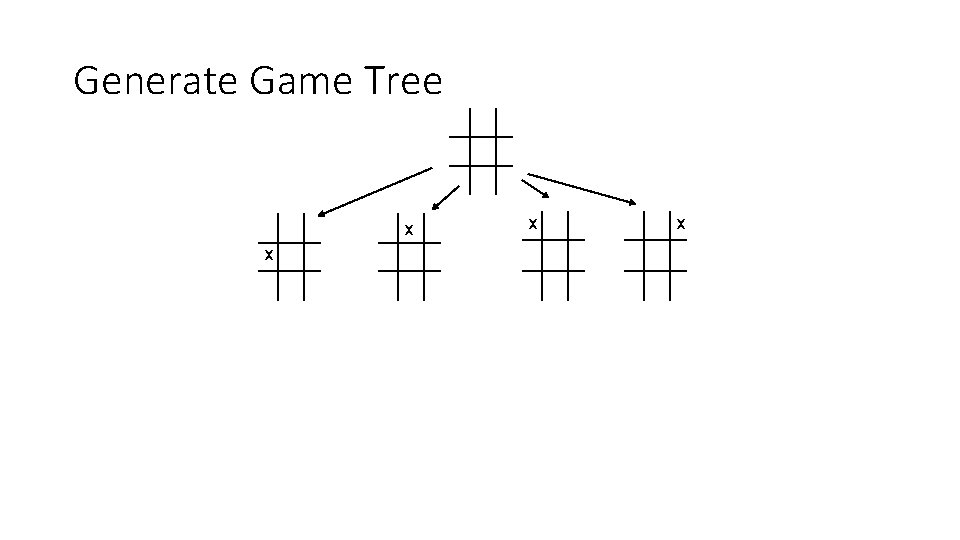



![- pruning: example 1 MAX [-∞, +∞] MIN CS 561 - Lecture 7 -8 - pruning: example 1 MAX [-∞, +∞] MIN CS 561 - Lecture 7 -8](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-29.jpg)
![- pruning: example 1 [-∞, +∞] MAX MIN 3 CS 561 - Lecture 7 - pruning: example 1 [-∞, +∞] MAX MIN 3 CS 561 - Lecture 7](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-30.jpg)
![- pruning: example 1 [-∞, +∞] MAX MIN [-∞, 3] 3 CS 561 - - pruning: example 1 [-∞, +∞] MAX MIN [-∞, 3] 3 CS 561 -](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-31.jpg)
![- pruning: example 1 [-∞, +∞] MAX MIN [-∞, 3] 3 12 CS 561 - pruning: example 1 [-∞, +∞] MAX MIN [-∞, 3] 3 12 CS 561](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-32.jpg)
![- pruning: example 1 [-∞, +∞] [3, +∞] MAX MIN [-∞, 3] 3 12 - pruning: example 1 [-∞, +∞] [3, +∞] MAX MIN [-∞, 3] 3 12](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-33.jpg)
![- pruning: example 1 [-∞, +∞] [3, +∞] MAX MIN [3, 2] [-∞, 3] - pruning: example 1 [-∞, +∞] [3, +∞] MAX MIN [3, 2] [-∞, 3]](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-34.jpg)
![- pruning: example 1 [-∞, +∞] [3, +∞] MAX MIN [3, 2] [-∞, 3] - pruning: example 1 [-∞, +∞] [3, +∞] MAX MIN [3, 2] [-∞, 3]](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-35.jpg)
![- pruning: example 1 [-∞, +∞] [3, +∞] MAX MIN [3, 2] [-∞, 3] - pruning: example 1 [-∞, +∞] [3, +∞] MAX MIN [3, 2] [-∞, 3]](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-36.jpg)
![- pruning: example 1 [-∞, +∞] [3, +∞] MAX MIN [3, 2] [-∞, 3] - pruning: example 1 [-∞, +∞] [3, +∞] MAX MIN [3, 2] [-∞, 3]](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-37.jpg)
![- pruning: example 1 [-∞, +∞] [3, +∞] MAX Selected move MIN [3, 2] - pruning: example 1 [-∞, +∞] [3, +∞] MAX Selected move MIN [3, 2]](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-38.jpg)
![- pruning: example 2 MAX [-∞, +∞] MIN CS 561 - Lecture 7 -8 - pruning: example 2 MAX [-∞, +∞] MIN CS 561 - Lecture 7 -8](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-39.jpg)
![- pruning: example 2 MAX [-∞, +∞] [-∞, 2] MIN 2 CS 561 - - pruning: example 2 MAX [-∞, +∞] [-∞, 2] MIN 2 CS 561 -](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-40.jpg)
![- pruning: example 2 MAX [-∞, +∞] [-∞, 2] MIN 5 CS 561 - - pruning: example 2 MAX [-∞, +∞] [-∞, 2] MIN 5 CS 561 -](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-41.jpg)
![- pruning: example 2 MAX [-∞, +∞] [2, +∞] [-∞, 2] MIN 14 CS - pruning: example 2 MAX [-∞, +∞] [2, +∞] [-∞, 2] MIN 14 CS](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-42.jpg)
![- pruning: example 2 MAX [-∞, +∞] [2, +∞] MIN [2, 5] 5 [-∞, - pruning: example 2 MAX [-∞, +∞] [2, +∞] MIN [2, 5] 5 [-∞,](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-43.jpg)
![- pruning: example 2 MAX [-∞, +∞] [2, +∞] MIN [2, 5] [2, 1] - pruning: example 2 MAX [-∞, +∞] [2, +∞] MIN [2, 5] [2, 1]](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-44.jpg)
![- pruning: example 2 [-∞, +∞] [2, +∞] MAX MIN [2, 8] 8 [-∞, - pruning: example 2 [-∞, +∞] [2, +∞] MAX MIN [2, 8] 8 [-∞,](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-45.jpg)
![- pruning: example 2 [-∞, +∞] [2, +∞] MAX MIN [2, 8] 12 8 - pruning: example 2 [-∞, +∞] [2, +∞] MAX MIN [2, 8] 12 8](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-46.jpg)
![- pruning: example 2 [-∞, +∞] [2, +∞] [3, +∞] MAX MIN [2, 8] - pruning: example 2 [-∞, +∞] [2, +∞] [3, +∞] MAX MIN [2, 8]](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-47.jpg)
![- pruning: example 2 [-∞, +∞] [2, +∞] [3, +∞] MAX Selected move MIN - pruning: example 2 [-∞, +∞] [2, +∞] [3, +∞] MAX Selected move MIN](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-48.jpg)
![- pruning: example 3 MIN MAX [6, ∞] MIN CS 561 - Lecture 7 - pruning: example 3 MIN MAX [6, ∞] MIN CS 561 - Lecture 7](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-49.jpg)
![- pruning: example 3 [-∞, 6] MIN MAX [6, ∞] [-∞, 6] MIN CS - pruning: example 3 [-∞, 6] MIN MAX [6, ∞] [-∞, 6] MIN CS](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-50.jpg)
![- pruning: example 3 [-∞, 6] MIN MAX [6, ∞] MIN [-∞, 14] [-∞, - pruning: example 3 [-∞, 6] MIN MAX [6, ∞] MIN [-∞, 14] [-∞,](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-51.jpg)
![- pruning: example 3 [-∞, 6] MIN MAX [6, ∞] MIN [-∞, 6] [-∞, - pruning: example 3 [-∞, 6] MIN MAX [6, ∞] MIN [-∞, 6] [-∞,](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-52.jpg)
![- pruning: example 3 [-∞, 6] MIN MAX [6, ∞] MIN [5, 6] [-∞, - pruning: example 3 [-∞, 6] MIN MAX [6, ∞] MIN [5, 6] [-∞,](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-53.jpg)
![- pruning: example 3 [-∞, 6] MIN MAX [5, 6] [6, ∞] MIN [-∞, - pruning: example 3 [-∞, 6] MIN MAX [5, 6] [6, ∞] MIN [-∞,](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-54.jpg)
![- pruning: example 3 [-∞, 6] MIN MAX [5, 6] [6, ∞] MIN [-∞, - pruning: example 3 [-∞, 6] MIN MAX [5, 6] [6, ∞] MIN [-∞,](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-55.jpg)
![- pruning: example 3 [-∞, 6] [-∞, 5] MIN MAX [5, 6] [6, ∞] - pruning: example 3 [-∞, 6] [-∞, 5] MIN MAX [5, 6] [6, ∞]](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-56.jpg)
![- pruning: example 3 [-∞, 6] [-∞, 5] MIN Selected move MAX [5, 6] - pruning: example 3 [-∞, 6] [-∞, 5] MIN Selected move MAX [5, 6]](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-57.jpg)
![- pruning: example 4 MIN MAX [6, ∞] MIN CS 561 - Lecture 7 - pruning: example 4 MIN MAX [6, ∞] MIN CS 561 - Lecture 7](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-58.jpg)
![- pruning: example 4 [-∞, 6] MIN MAX [6, ∞] [-∞, 6] MIN CS - pruning: example 4 [-∞, 6] MIN MAX [6, ∞] [-∞, 6] MIN CS](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-59.jpg)
![- pruning: example 4 [-∞, 6] MIN MAX [6, ∞] MIN [-∞, 14] [-∞, - pruning: example 4 [-∞, 6] MIN MAX [6, ∞] MIN [-∞, 14] [-∞,](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-60.jpg)
![- pruning: example 4 [-∞, 6] MIN MAX [6, ∞] MIN [-∞, 6] [-∞, - pruning: example 4 [-∞, 6] MIN MAX [6, ∞] MIN [-∞, 6] [-∞,](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-61.jpg)
![- pruning: example 4 [-∞, 6] MIN MAX [6, ∞] MIN [7, 6] [-∞, - pruning: example 4 [-∞, 6] MIN MAX [6, ∞] MIN [7, 6] [-∞,](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-62.jpg)
![- pruning: example 4 [-∞, 6] MIN Selected move MAX [6, ∞] MIN [7, - pruning: example 4 [-∞, 6] MIN Selected move MAX [6, ∞] MIN [7,](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-63.jpg)








- Slides: 78

Adversarial Search

Adversarial Search Game playing • Perfect play • The minimax algorithm • alpha-beta pruning • Resource limitations • Elements of chance • Imperfect information

Game Playing State-of-the-Art • Checkers: Chinook ended 40 -year-reign of human world champion Marion Tinsley in 1994. Used an endgame database defining perfect play for all positions involving 8 or fewer pieces on the board, a total of 443, 748, 401, 247 positions. Checkers is now solved! • Chess: Deep Blue defeated human world champion Gary Kasparov in a sixgame match in 1997. Deep Blue examined 200 million positions per second, used very sophisticated evaluation and undisclosed methods for extending some lines of search up to 40 ply. Current programs are even better, if less historic. • Othello: Human champions refuse to compete against computers, which are too good. • Go: Human champions are beginning to be challenged by machines, though the best humans still beat the best machines. In go, b > 300, so most programs use pattern knowledge bases to suggest plausible moves, along with aggressive pruning. • Pacman: unknown

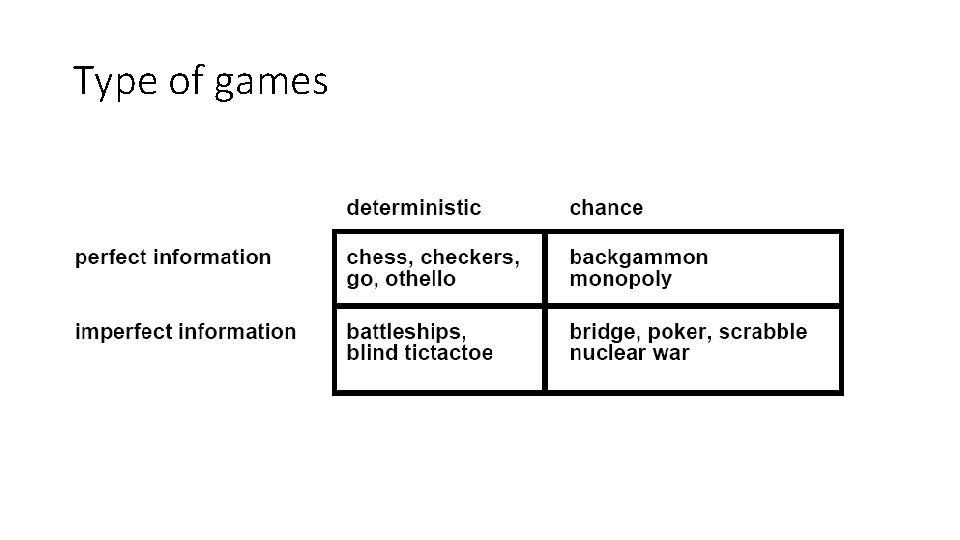
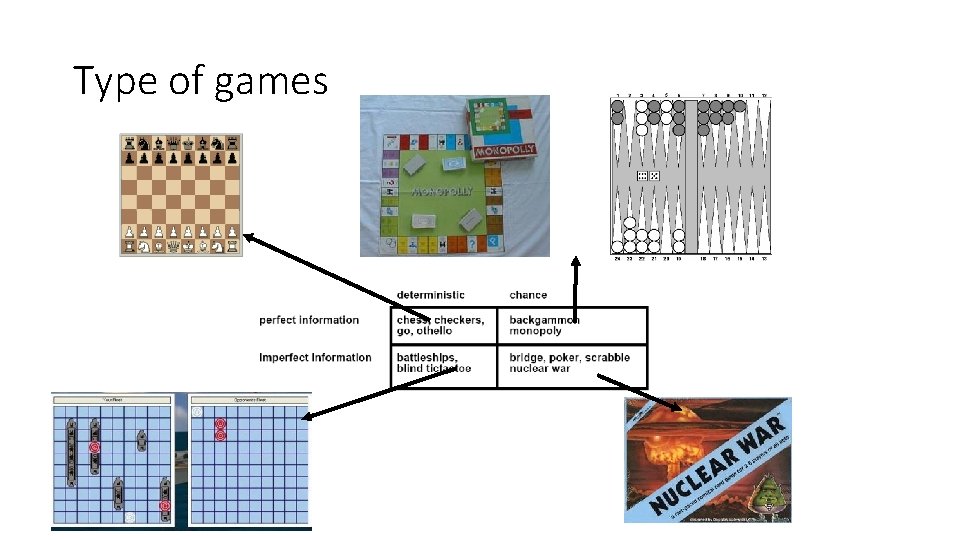
What kind of games? • Abstraction: To describe a game we must capture every relevant aspect of the game. Such as: • Chess • Tic-tac-toe • … • Accessible environments: Such games are characterized by perfect information • Search: game-playing then consists of a search through possible game positions • Unpredictable opponent: introduces uncertainty thus game-playing must deal with contingency problems

Type of games

Type of games

Game Playing • Many different kinds of games! • Axes: • • Deterministic or stochastic? One, two, or more players? Perfect information (can you see the state)? Turn taking or simultaneous action? • Want algorithms for calculating a strategy (policy) which recommends a move in each state

Deterministic Games • Deterministic, single player, perfect information: • • Know the rules Know what actions do Know when you win E. g. Freecell, 8 -Puzzle, Rubik’s cube • … it’s just search! • Slight reinterpretation: • Each node stores a value: the best outcome it can reach • This is the maximal outcome of its children (the max value) • Note that we don’t have path sums as before (utilities at end) • After search, can pick move that leads to best node

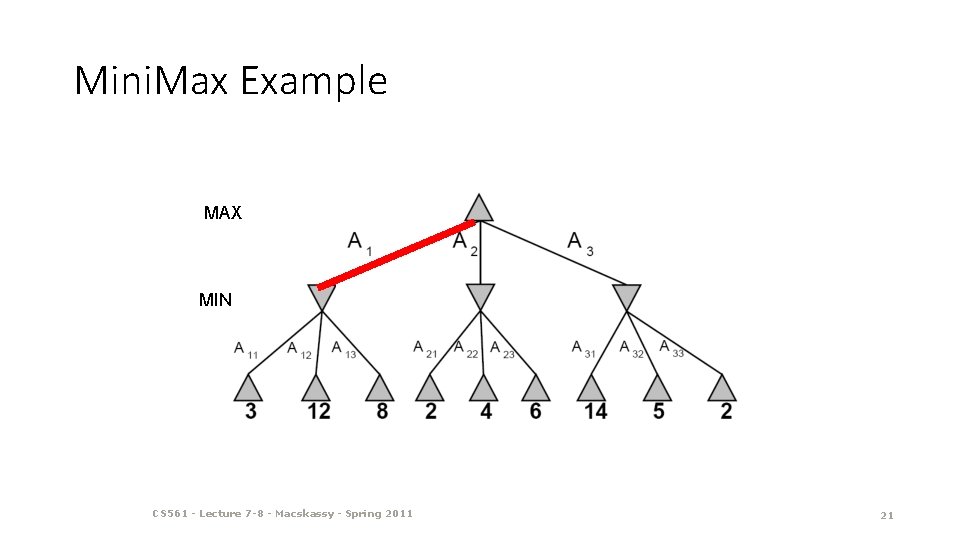
Deterministic Two-Player • E. g. tic-tac-toe, chess, checkers • Zero-sum games • One player maximizes result • The other minimizes result • Minimax search • • A state-space search tree Players alternate Each layer, or ply, consists of around of moves* Choose move to position with highest minimax value = best achievable utility against best play

Games vs. search problems · “Unpredictable" opponent solution is a strategy specifying a move for every possible opponent reply · Time limits unlikely to find goal, must approximate · Plan of attack: ◦ Computer considers possible lines of play (Babbage, 1846) ◦ Algorithm for perfect play (Zermelo, 1912; Von Neumann, 1944) ◦ Finite horizon, approximate evaluation (Zuse, 1945; Wiener, 1948; Shannon, 1950) ◦ First chess program (Turing, 1951) ◦ Machine learning to improve evaluation accuracy (Samuel, 1952 - 57) ◦ Pruning to allow deeper search (Mc. Carthy, 1956)

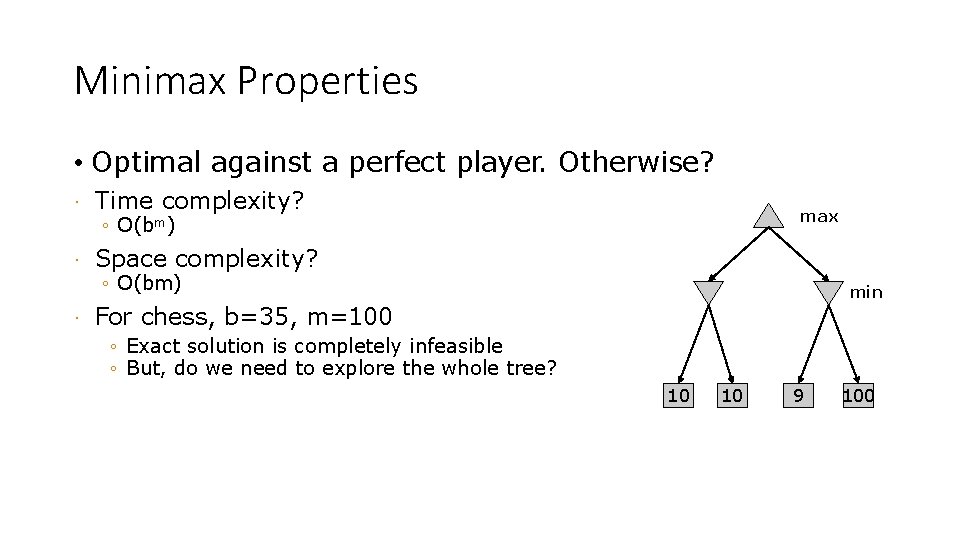
Searching for the next move · Complexity: many games have a huge search space • Chess: b = 35, m=100 nodes = 35 100 • if each node takes about 1 ns to explore then each move will take about 10 50 millennia to calculate. Resource (e. g. , time, memory) limit: optimal solution not feasible/possible, thus must approximate 1. Pruning: makes the search more efficient by discarding portions of the search tree that cannot improve quality result. 2. Evaluation functions: heuristics to evaluate utility of a state without exhaustive search. ·

Two-player games • A game formulated as a search problem ◦ ◦ Initial state: Operators: Terminal state: Utility function: of the board position and turn definition of legal moves conditions for when game is over a numeric value that describes the outcome game. E. g. , -1, 0, 1 for loss, draw, win. (AKA payoff function)

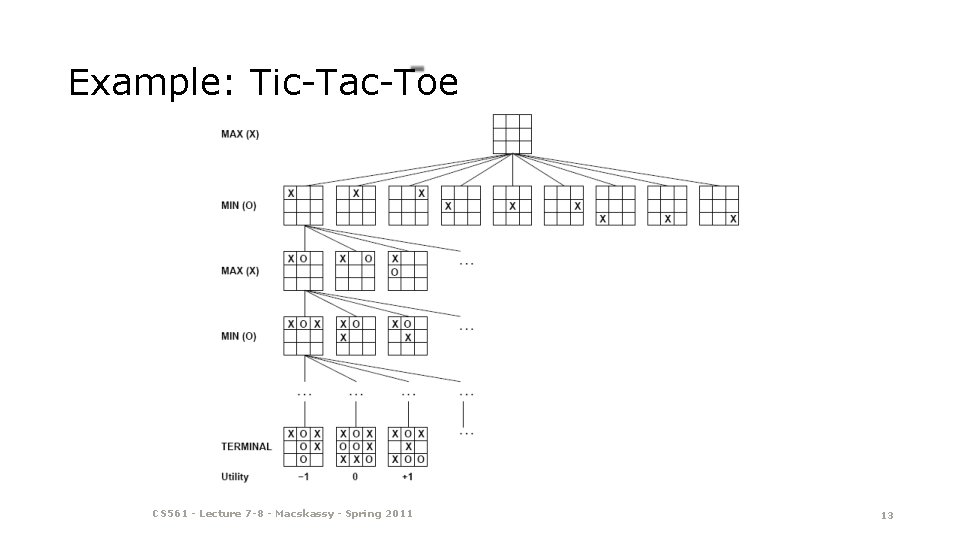
Example: Tic-Tac-Toe CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 13

The minimax algorithm · · Perfect play for deterministic environments with perfect information Basic idea: choose move with highest minimax value · • = best achievable payoff against best play Algorithm: 1. Generate game tree completely 2. Determine utility of each terminal state 3. Propagate the utility values upward in the three by applying • MIN and MAX operators on the nodes in the current level 4. At the root node use minimax decision to select the move • with the max (of the min) utility value · Steps 2 and 3 in the algorithm assume that the opponent will play perfectly.

Generate Game Tree
Generate Game Tree x x

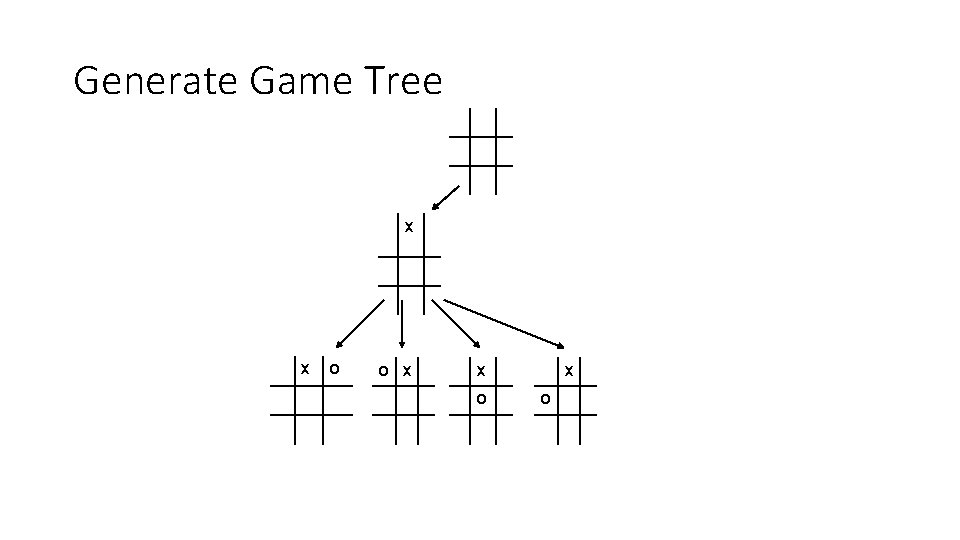
Generate Game Tree x x o o x x o

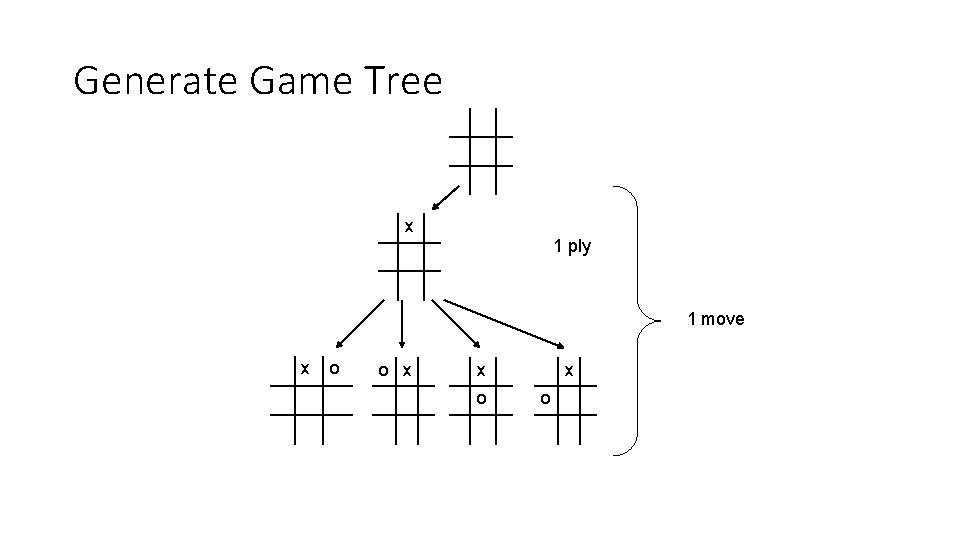
Generate Game Tree x 1 ply 1 move x o o x x o

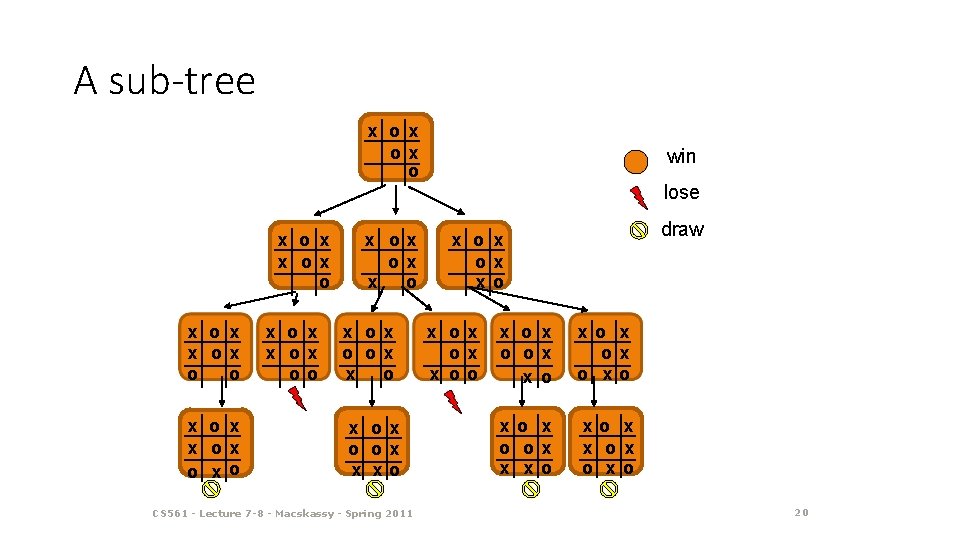
A sub-tree x ox o win lose x o x x ox o x o x x ox oo x ox ox x o x ox o ox x xo CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 draw x o x ox ox x oo x o ox x o x ox o xo x o ox x x ox o 20

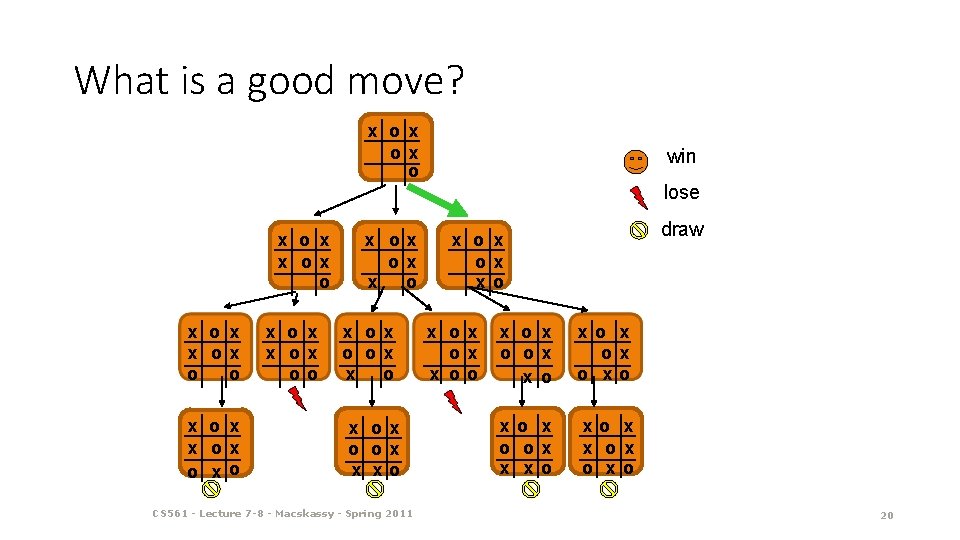
What is a good move? x ox o win lose x o x x ox o x o x x ox oo x ox ox x o x ox o ox x xo CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 draw x o x ox ox x oo x o ox x o x ox o xo x o ox x x ox o 20

Mini. Max Example MAX MIN CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 21

Mini. Max: Recursive Implementation CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 22

Minimax Properties • Optimal against a perfect player. Otherwise? · Time complexity? · Space complexity? · max ◦ O(bm) min For chess, b=35, m=100 ◦ Exact solution is completely infeasible ◦ But, do we need to explore the whole tree? 10 10 9 100

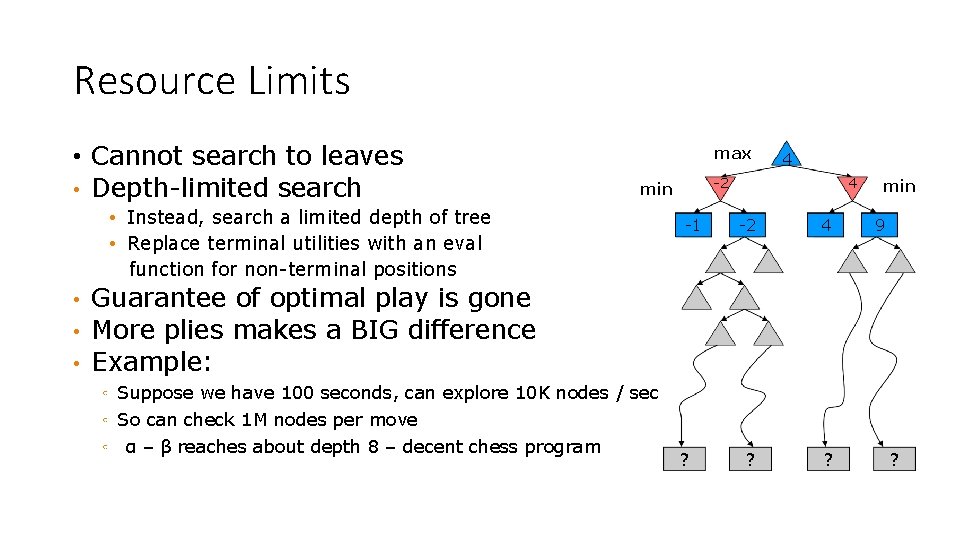
Resource Limits • Cannot search to leaves • Depth-limited search max • • • -2 min • Instead, search a limited depth of tree • Replace terminal utilities with an eval function for non-terminal positions 4 -1 4 -2 4 ? ? min 9 Guarantee of optimal play is gone More plies makes a BIG difference Example: ◦ Suppose we have 100 seconds, can explore 10 K nodes / sec ◦ So can check 1 M nodes per move ◦ α – β reaches about depth 8 – decent chess program ? ?

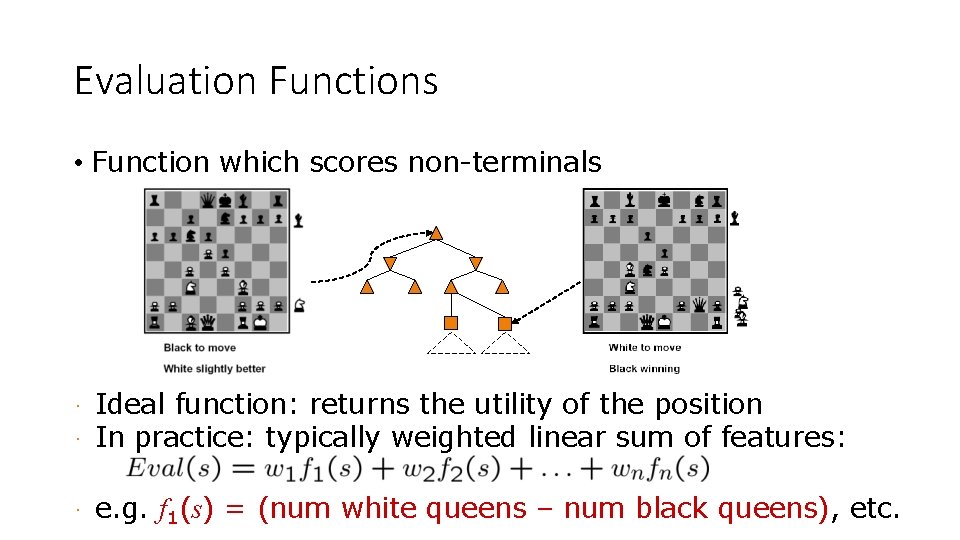
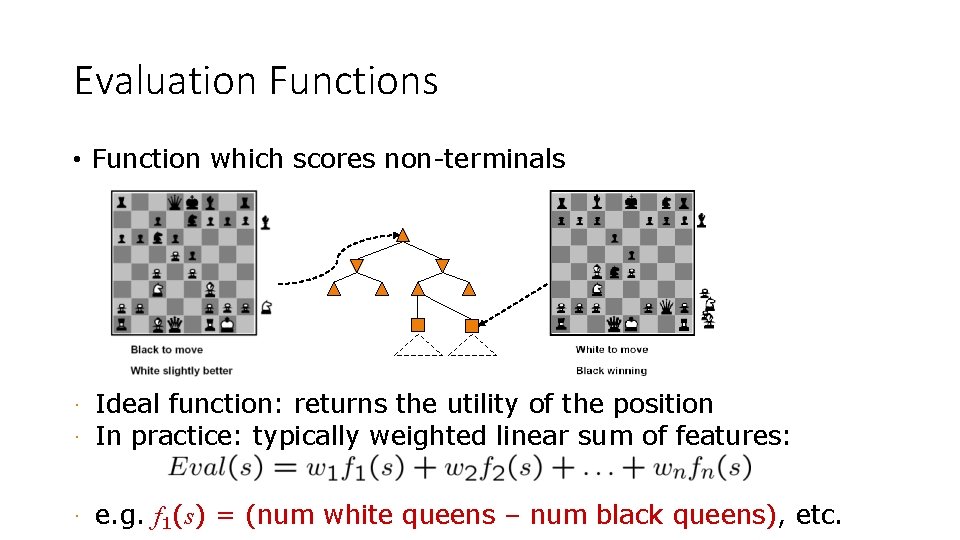
Evaluation Functions • Function which scores non-terminals · · Ideal function: returns the utility of the position In practice: typically weighted linear sum of features: · e. g. f 1(s) = (num white queens – num black queens), etc.

Evaluation Functions

Why Pacman starves He knows his score will go up by eating the dot now · He knows his score will go up just as much by eating the dot later on · There are no point- scoring opportunities after eating the dot · Therefore, waiting seems just as good as eating ·

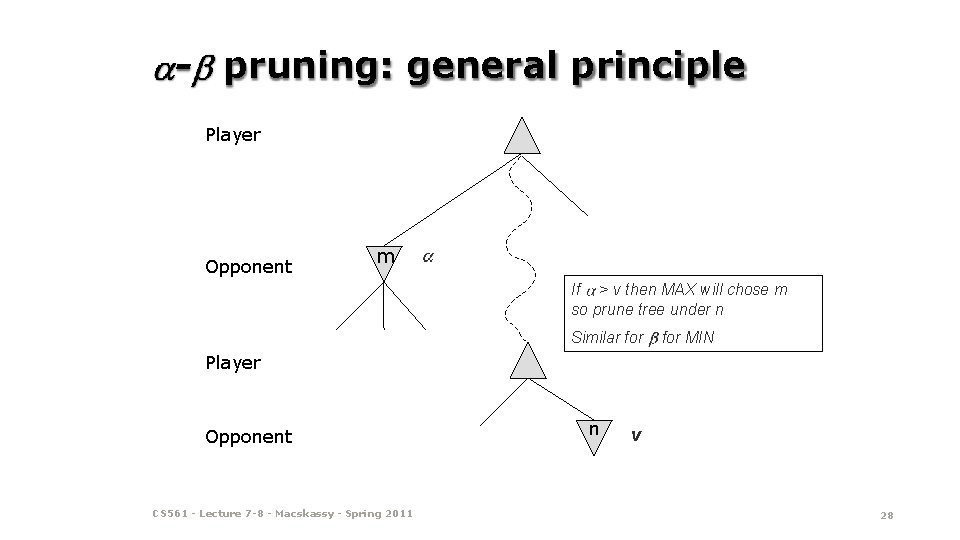
- pruning: general principle Player Opponent m If > v then MAX will chose m so prune tree under n Similar for MIN Player Opponent CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 n v 28
![pruning example 1 MAX MIN CS 561 Lecture 7 8 - pruning: example 1 MAX [-∞, +∞] MIN CS 561 - Lecture 7 -8](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-29.jpg)
- pruning: example 1 MAX [-∞, +∞] MIN CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 30
![pruning example 1 MAX MIN 3 CS 561 Lecture 7 - pruning: example 1 [-∞, +∞] MAX MIN 3 CS 561 - Lecture 7](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-30.jpg)
- pruning: example 1 [-∞, +∞] MAX MIN 3 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 30
![pruning example 1 MAX MIN 3 3 CS 561 - pruning: example 1 [-∞, +∞] MAX MIN [-∞, 3] 3 CS 561 -](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-31.jpg)
- pruning: example 1 [-∞, +∞] MAX MIN [-∞, 3] 3 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 31
![pruning example 1 MAX MIN 3 3 12 CS 561 - pruning: example 1 [-∞, +∞] MAX MIN [-∞, 3] 3 12 CS 561](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-32.jpg)
- pruning: example 1 [-∞, +∞] MAX MIN [-∞, 3] 3 12 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 32
![pruning example 1 3 MAX MIN 3 3 12 - pruning: example 1 [-∞, +∞] [3, +∞] MAX MIN [-∞, 3] 3 12](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-33.jpg)
- pruning: example 1 [-∞, +∞] [3, +∞] MAX MIN [-∞, 3] 3 12 8 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 33
![pruning example 1 3 MAX MIN 3 2 3 - pruning: example 1 [-∞, +∞] [3, +∞] MAX MIN [3, 2] [-∞, 3]](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-34.jpg)
- pruning: example 1 [-∞, +∞] [3, +∞] MAX MIN [3, 2] [-∞, 3] 3 12 8 2 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 34
![pruning example 1 3 MAX MIN 3 2 3 - pruning: example 1 [-∞, +∞] [3, +∞] MAX MIN [3, 2] [-∞, 3]](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-35.jpg)
- pruning: example 1 [-∞, +∞] [3, +∞] MAX MIN [3, 2] [-∞, 3] 3 12 8 2 [3, 14] 14 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 35
![pruning example 1 3 MAX MIN 3 2 3 - pruning: example 1 [-∞, +∞] [3, +∞] MAX MIN [3, 2] [-∞, 3]](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-36.jpg)
- pruning: example 1 [-∞, +∞] [3, +∞] MAX MIN [3, 2] [-∞, 3] 3 12 8 2 [3, 14] [3, 5] 14 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 5 36
![pruning example 1 3 MAX MIN 3 2 3 - pruning: example 1 [-∞, +∞] [3, +∞] MAX MIN [3, 2] [-∞, 3]](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-37.jpg)
- pruning: example 1 [-∞, +∞] [3, +∞] MAX MIN [3, 2] [-∞, 3] 3 12 8 2 [3, 14] [3, 5] [3, 2] 14 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 5 2 37
![pruning example 1 3 MAX Selected move MIN 3 2 - pruning: example 1 [-∞, +∞] [3, +∞] MAX Selected move MIN [3, 2]](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-38.jpg)
- pruning: example 1 [-∞, +∞] [3, +∞] MAX Selected move MIN [3, 2] [-∞, 3] 3 12 8 2 [3, 14] [3, 5] [3, 2] 14 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 5 2 38
![pruning example 2 MAX MIN CS 561 Lecture 7 8 - pruning: example 2 MAX [-∞, +∞] MIN CS 561 - Lecture 7 -8](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-39.jpg)
- pruning: example 2 MAX [-∞, +∞] MIN CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 40
![pruning example 2 MAX 2 MIN 2 CS 561 - pruning: example 2 MAX [-∞, +∞] [-∞, 2] MIN 2 CS 561 -](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-40.jpg)
- pruning: example 2 MAX [-∞, +∞] [-∞, 2] MIN 2 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 40
![pruning example 2 MAX 2 MIN 5 CS 561 - pruning: example 2 MAX [-∞, +∞] [-∞, 2] MIN 5 CS 561 -](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-41.jpg)
- pruning: example 2 MAX [-∞, +∞] [-∞, 2] MIN 5 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 2 41
![pruning example 2 MAX 2 2 MIN 14 CS - pruning: example 2 MAX [-∞, +∞] [2, +∞] [-∞, 2] MIN 14 CS](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-42.jpg)
- pruning: example 2 MAX [-∞, +∞] [2, +∞] [-∞, 2] MIN 14 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 5 2 42
![pruning example 2 MAX 2 MIN 2 5 5 - pruning: example 2 MAX [-∞, +∞] [2, +∞] MIN [2, 5] 5 [-∞,](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-43.jpg)
- pruning: example 2 MAX [-∞, +∞] [2, +∞] MIN [2, 5] 5 [-∞, 2] 14 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 5 2 43
![pruning example 2 MAX 2 MIN 2 5 2 1 - pruning: example 2 MAX [-∞, +∞] [2, +∞] MIN [2, 5] [2, 1]](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-44.jpg)
- pruning: example 2 MAX [-∞, +∞] [2, +∞] MIN [2, 5] [2, 1] 1 5 [-∞, 2] 14 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 5 2 44
![pruning example 2 2 MAX MIN 2 8 8 - pruning: example 2 [-∞, +∞] [2, +∞] MAX MIN [2, 8] 8 [-∞,](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-45.jpg)
- pruning: example 2 [-∞, +∞] [2, +∞] MAX MIN [2, 8] 8 [-∞, 2] [2, 5] [2, 1] 1 5 14 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 5 2 45
![pruning example 2 2 MAX MIN 2 8 12 8 - pruning: example 2 [-∞, +∞] [2, +∞] MAX MIN [2, 8] 12 8](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-46.jpg)
- pruning: example 2 [-∞, +∞] [2, +∞] MAX MIN [2, 8] 12 8 [-∞, 2] [2, 5] [2, 1] 1 5 14 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 5 2 46
![pruning example 2 2 3 MAX MIN 2 8 - pruning: example 2 [-∞, +∞] [2, +∞] [3, +∞] MAX MIN [2, 8]](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-47.jpg)
- pruning: example 2 [-∞, +∞] [2, +∞] [3, +∞] MAX MIN [2, 8] [2, 3] 3 12 8 [-∞, 2] [2, 5] [2, 1] 1 5 14 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 5 2 47
![pruning example 2 2 3 MAX Selected move MIN - pruning: example 2 [-∞, +∞] [2, +∞] [3, +∞] MAX Selected move MIN](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-48.jpg)
- pruning: example 2 [-∞, +∞] [2, +∞] [3, +∞] MAX Selected move MIN [2, 8] [2, 3] 3 12 8 [-∞, 2] [2, 5] [2, 1] 1 5 14 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 5 2 48
![pruning example 3 MIN MAX 6 MIN CS 561 Lecture 7 - pruning: example 3 MIN MAX [6, ∞] MIN CS 561 - Lecture 7](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-49.jpg)
- pruning: example 3 MIN MAX [6, ∞] MIN CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 50
![pruning example 3 6 MIN MAX 6 6 MIN CS - pruning: example 3 [-∞, 6] MIN MAX [6, ∞] [-∞, 6] MIN CS](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-50.jpg)
- pruning: example 3 [-∞, 6] MIN MAX [6, ∞] [-∞, 6] MIN CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 50
![pruning example 3 6 MIN MAX 6 MIN 14 - pruning: example 3 [-∞, 6] MIN MAX [6, ∞] MIN [-∞, 14] [-∞,](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-51.jpg)
- pruning: example 3 [-∞, 6] MIN MAX [6, ∞] MIN [-∞, 14] [-∞, 6] 14 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 51
![pruning example 3 6 MIN MAX 6 MIN 6 - pruning: example 3 [-∞, 6] MIN MAX [6, ∞] MIN [-∞, 6] [-∞,](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-52.jpg)
- pruning: example 3 [-∞, 6] MIN MAX [6, ∞] MIN [-∞, 6] [-∞, 14][-∞, 5] 14 5 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 52
![pruning example 3 6 MIN MAX 6 MIN 5 6 - pruning: example 3 [-∞, 6] MIN MAX [6, ∞] MIN [5, 6] [-∞,](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-53.jpg)
- pruning: example 3 [-∞, 6] MIN MAX [6, ∞] MIN [5, 6] [-∞, 14][-∞, 5] 14 5 9 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 53
![pruning example 3 6 MIN MAX 5 6 6 MIN - pruning: example 3 [-∞, 6] MIN MAX [5, 6] [6, ∞] MIN [-∞,](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-54.jpg)
- pruning: example 3 [-∞, 6] MIN MAX [5, 6] [6, ∞] MIN [-∞, 14][-∞, 5] 14 5 9 [5, 1] 1 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 54
![pruning example 3 6 MIN MAX 5 6 6 MIN - pruning: example 3 [-∞, 6] MIN MAX [5, 6] [6, ∞] MIN [-∞,](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-55.jpg)
- pruning: example 3 [-∞, 6] MIN MAX [5, 6] [6, ∞] MIN [-∞, 14][-∞, 5] 14 5 9 1 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 [5, 1] [5, 4] 4 55
![pruning example 3 6 5 MIN MAX 5 6 6 - pruning: example 3 [-∞, 6] [-∞, 5] MIN MAX [5, 6] [6, ∞]](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-56.jpg)
- pruning: example 3 [-∞, 6] [-∞, 5] MIN MAX [5, 6] [6, ∞] MIN [-∞, 14][-∞, 5] 14 5 9 1 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 [5, 1] [5, 4] 4 56
![pruning example 3 6 5 MIN Selected move MAX 5 6 - pruning: example 3 [-∞, 6] [-∞, 5] MIN Selected move MAX [5, 6]](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-57.jpg)
- pruning: example 3 [-∞, 6] [-∞, 5] MIN Selected move MAX [5, 6] [6, ∞] MIN [-∞, 14][-∞, 5] 14 5 9 1 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 [5, 1] [5, 4] 4 57
![pruning example 4 MIN MAX 6 MIN CS 561 Lecture 7 - pruning: example 4 MIN MAX [6, ∞] MIN CS 561 - Lecture 7](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-58.jpg)
- pruning: example 4 MIN MAX [6, ∞] MIN CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 59
![pruning example 4 6 MIN MAX 6 6 MIN CS - pruning: example 4 [-∞, 6] MIN MAX [6, ∞] [-∞, 6] MIN CS](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-59.jpg)
- pruning: example 4 [-∞, 6] MIN MAX [6, ∞] [-∞, 6] MIN CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 60
![pruning example 4 6 MIN MAX 6 MIN 14 - pruning: example 4 [-∞, 6] MIN MAX [6, ∞] MIN [-∞, 14] [-∞,](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-60.jpg)
- pruning: example 4 [-∞, 6] MIN MAX [6, ∞] MIN [-∞, 14] [-∞, 6] 14 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 60
![pruning example 4 6 MIN MAX 6 MIN 6 - pruning: example 4 [-∞, 6] MIN MAX [6, ∞] MIN [-∞, 6] [-∞,](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-61.jpg)
- pruning: example 4 [-∞, 6] MIN MAX [6, ∞] MIN [-∞, 6] [-∞, 14][-∞, 7] 14 7 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 61
![pruning example 4 6 MIN MAX 6 MIN 7 6 - pruning: example 4 [-∞, 6] MIN MAX [6, ∞] MIN [7, 6] [-∞,](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-62.jpg)
- pruning: example 4 [-∞, 6] MIN MAX [6, ∞] MIN [7, 6] [-∞, 14][-∞, 7] 14 7 9 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 62
![pruning example 4 6 MIN Selected move MAX 6 MIN 7 - pruning: example 4 [-∞, 6] MIN Selected move MAX [6, ∞] MIN [7,](https://slidetodoc.com/presentation_image_h2/13e781836e270a06a3e52ae07366dcfc/image-63.jpg)
- pruning: example 4 [-∞, 6] MIN Selected move MAX [6, ∞] MIN [7, 6] [-∞, 14][-∞, 7] 14 7 9 CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 63

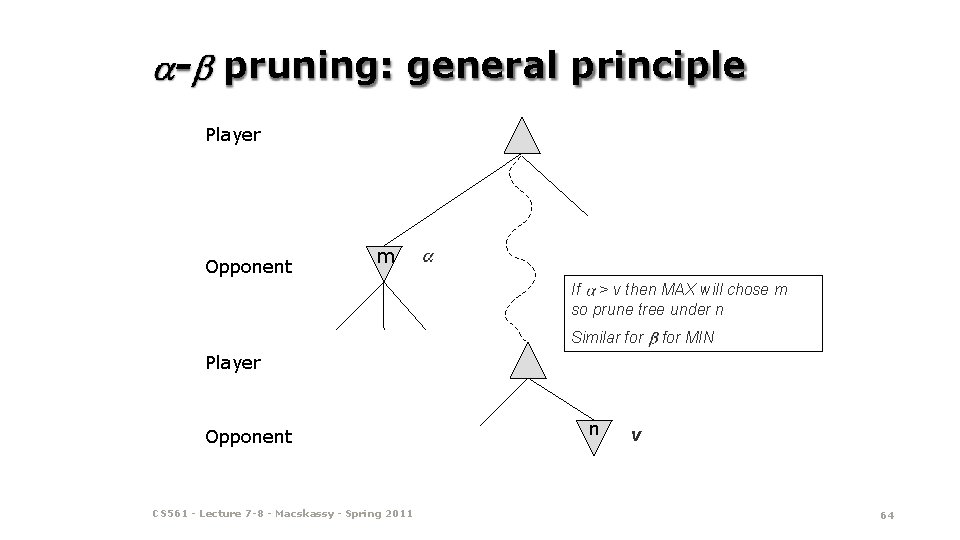
- pruning: general principle Player Opponent m If > v then MAX will chose m so prune tree under n Similar for MIN Player Opponent CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 n v 64

The α – β algorithm

Properties α – β algorithm

Resource limits · Standard approach: ◦ Use CUTOFF-TEST instead of TERMINAL-TEST · e. g. , depth limit (perhaps add quiescence search) ◦ Use EVAL instead of UTILITY · i. e. , evaluation function that estimates desirability of position · Suppose we have 100 seconds, and can explore 104 nodes/second 106 nodes per move ≈ 358/2 α – β reaches depth 8 pretty good chess program

Evaluation Functions • Function which scores non-terminals Ideal function: returns the utility of the position · In practice: typically weighted linear sum of features: · · e. g. f 1(s) = (num white queens – num black queens), etc.

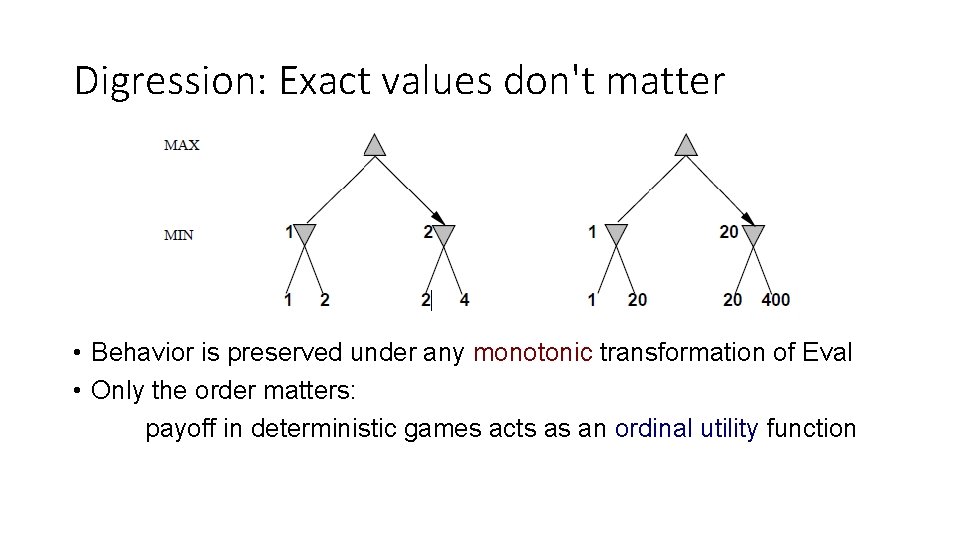
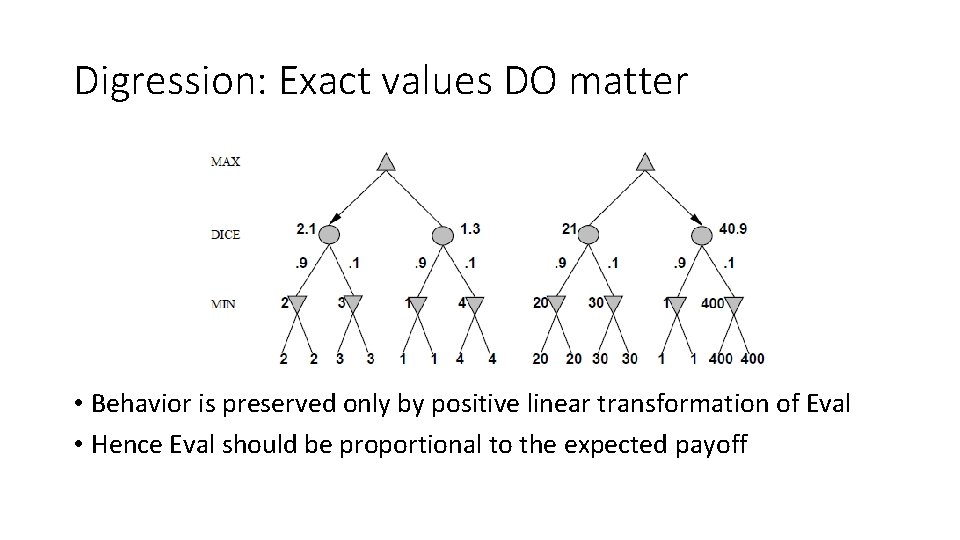
Digression: Exact values don't matter • Behavior is preserved under any monotonic transformation of Eval • Only the order matters: payoff in deterministic games acts as an ordinal utility function

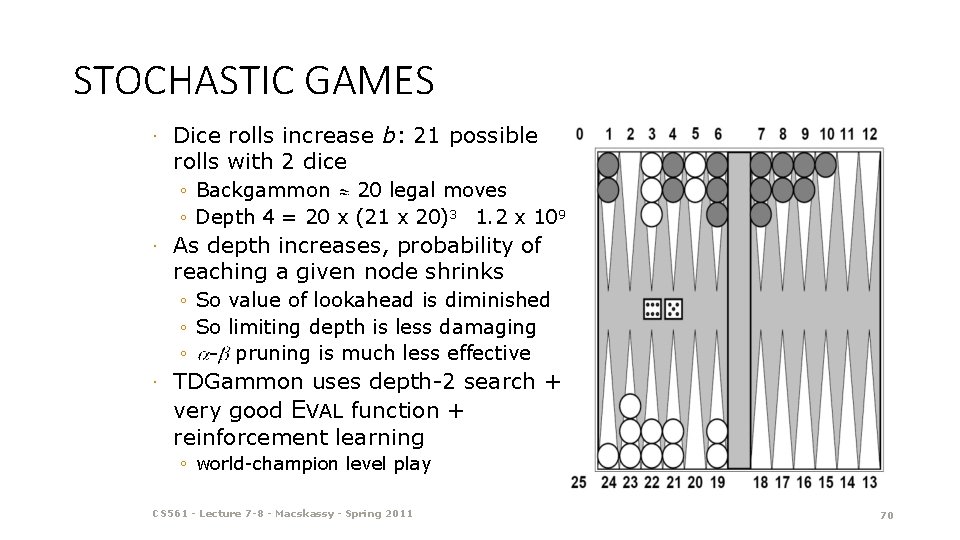
STOCHASTIC GAMES · Dice rolls increase b: 21 possible rolls with 2 dice ◦ Backgammon 20 legal moves ◦ Depth 4 = 20 x (21 x 20)3 1. 2 x 109 · As depth increases, probability of reaching a given node shrinks ◦ So value of lookahead is diminished ◦ So limiting depth is less damaging ◦ - pruning is much less effective · TDGammon uses depth-2 search + very good EVAL function + reinforcement learning ◦ world-champion level play CS 561 - Lecture 7 -8 - Macskassy - Spring 2011 70

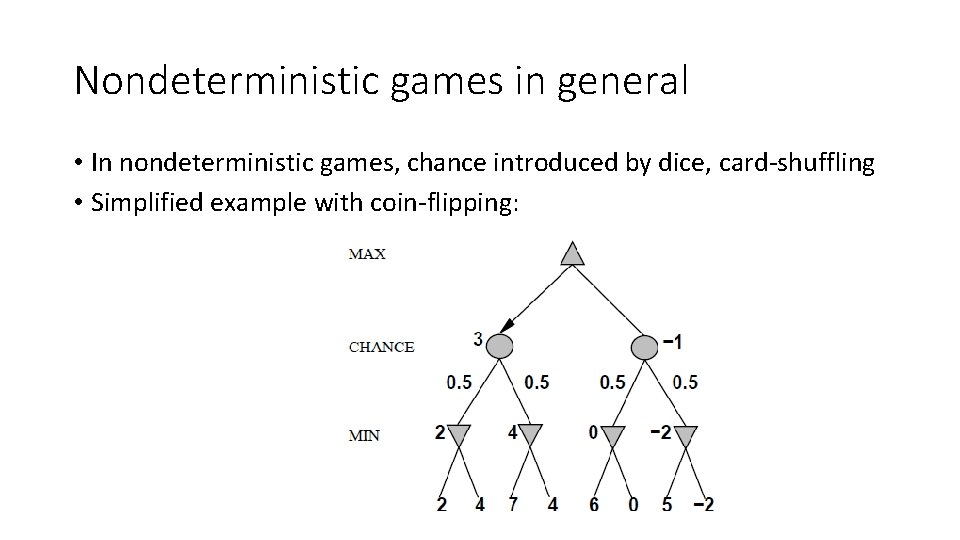
Nondeterministic games in general • In nondeterministic games, chance introduced by dice, card-shuffling • Simplified example with coin-flipping:

Algorithm for nondeterministic games • Expectiminimax gives perfect play • Just like Minimax, except we must also handle chance nodes: • … • if state is a Max node then • return the highest Expecti. Minimax-Value of Successors(state) • if state is a Min node then • return the lowest Expecti. Minimax-Value of Successors(state) • if state is a chance node then • return average of Expecti. Minimax-Value of Successors(state) • …

Expectiminimax

Digression: Exact values DO matter • Behavior is preserved only by positive linear transformation of Eval • Hence Eval should be proportional to the expected payoff

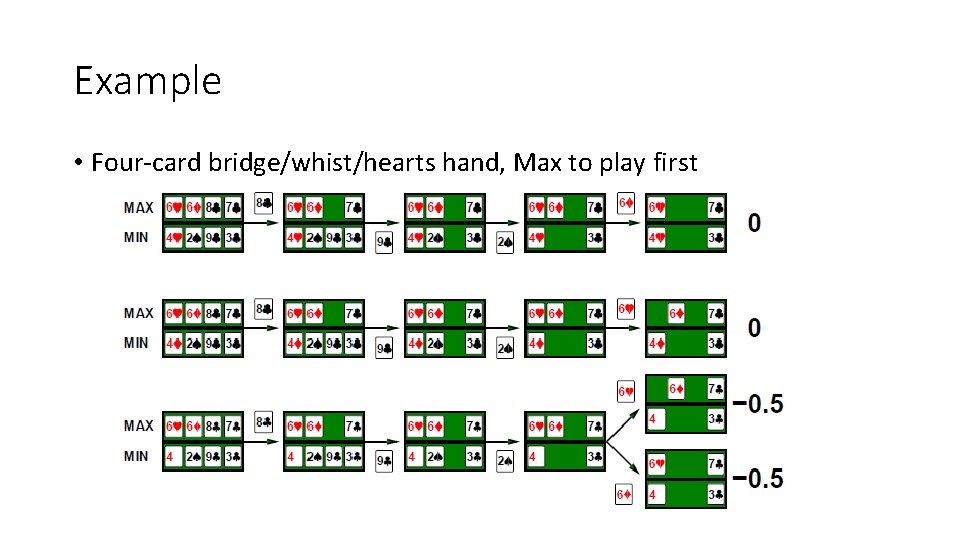
Games of imperfect information • E. g. , card games, where opponent's initial cards are unknown • Typically we can calculate a probability for each possible deal • Seems just like having one big dice roll at the beginning of the game • Idea: compute the minimax value of each action in each deal, then choose the action with highest expected value over all deals • Special case: if an action is optimal for all deals, it's optimal. • GIB, current best bridge program, approximates this idea by 1) generating 100 deals consistent with bidding information 2) picking the action that wins most tricks on average

Example • Four-card bridge/whist/hearts hand, Max to play first

Commonsense example

Proper analysis • * Intuition that the value of an action is the average of its values in all actual states is WRONG • With partial observability, value of an action depends on the information state or belief state the agent is in • Can generate and search a tree of information states • Leads to rational behaviors such as • Acting to obtain information • Signalling to one's partner • Acting randomly to minimize information disclosure
 Adversarial search problems uses
Adversarial search problems uses Playing a decent game of table tennis (ping-pong)
Playing a decent game of table tennis (ping-pong) Foreshadowing in the most dangerous game
Foreshadowing in the most dangerous game Segundo o estudo sobre past continuous
Segundo o estudo sobre past continuous Jillian and dawn are playing a game
Jillian and dawn are playing a game Greek vase shapes
Greek vase shapes Perfect present
Perfect present I've got a friend we like to play we play together
I've got a friend we like to play we play together Play random play basketball
Play random play basketball Play by play
Play by play Play within the play hamlet
Play within the play hamlet Rose hsu jordan
Rose hsu jordan Cannibal and missionaries game
Cannibal and missionaries game Fictitious play
Fictitious play How to play steal the pile card game
How to play steal the pile card game Let's play a game
Let's play a game Play out game
Play out game How to play any mental game
How to play any mental game Present perfect unit 7 answers
Present perfect unit 7 answers Site:slidetodoc.com
Site:slidetodoc.com Paint in simple past
Paint in simple past Adversarial stakeholders
Adversarial stakeholders The adversarial system
The adversarial system What is an adversary system
What is an adversary system Hexiangnan
Hexiangnan Pgd
Pgd Quantum generative adversarial learning
Quantum generative adversarial learning Neur ips
Neur ips Adversarial interview
Adversarial interview Adversarial system law definition
Adversarial system law definition Adversarial examples
Adversarial examples Singing
Singing Spectral normalization gan
Spectral normalization gan Generative adversarial networks
Generative adversarial networks Adversarial multi-task learning for text classification
Adversarial multi-task learning for text classification Voice conversion
Voice conversion Adversarial training
Adversarial training Nicolas papernot
Nicolas papernot The limitations of deep learning in adversarial settings.
The limitations of deep learning in adversarial settings. Adversarial patch
Adversarial patch Unsupervised image to image translation
Unsupervised image to image translation The pirate game sheet
The pirate game sheet The farming game instructions
The farming game instructions A formal approach to game design and game research
A formal approach to game design and game research Game lab game theory
Game lab game theory Liar game game theory
Liar game game theory Liar game game theory
Liar game game theory Diagram on the playing area in volleyball
Diagram on the playing area in volleyball I like playing badminton
I like playing badminton Achilles and ajax playing dice
Achilles and ajax playing dice Example of rubrics in role playing
Example of rubrics in role playing What s your hobby
What s your hobby Yesterday evening reported speech
Yesterday evening reported speech Role playing dimension power bi
Role playing dimension power bi Playing nice in the sandbox
Playing nice in the sandbox Jesus and satan playing chess
Jesus and satan playing chess Process oriented rubric example
Process oriented rubric example I meet john in town yesterday
I meet john in town yesterday German kids playing with money
German kids playing with money Barry liked playing board games
Barry liked playing board games Playing god (ethics)
Playing god (ethics) Even playing field meaning
Even playing field meaning My hobby is keeping fish. i have a modest
My hobby is keeping fish. i have a modest Variable interval
Variable interval Do not confuse theme with a story's
Do not confuse theme with a story's Juan continued playing although he injured his knee
Juan continued playing although he injured his knee Four square rules cherry bomb
Four square rules cherry bomb Whats a main idea
Whats a main idea He likes playing table tennis
He likes playing table tennis Batos taino
Batos taino Red queen in deck of cards
Red queen in deck of cards Sintaks role playing
Sintaks role playing How to play guitar by ear
How to play guitar by ear Present simple play football
Present simple play football 1. when i phoned my friends, they (play) ..........monopoly
1. when i phoned my friends, they (play) ..........monopoly Illusions for kids
Illusions for kids I am playing football
I am playing football Quia conjunctions rags to riches
Quia conjunctions rags to riches Children playing
Children playing