How to play ANY mental game A Completeness

How to play ANY mental game A Completeness Theorem for Protocols with Honest Majority

Overview 1. Introduction 2. Solution for TM-Games 2. 1. for passive adversaries 2. 2. for malicious adversaries 3. General games 4. Summary

1. Introduction • Motivation: n Players want to compute • Problem: each is a private input of the player i • Question: Is it possible to run M so that 1. The output is correct 2. No additional information of the leaked is

1. Introduction • Adversaries: - passive Adversaries: Run the protocol correct but run „on the side“ other efficient algorithmns - malicious Adversaries: Replace the algorithm by any efficient algorithm

1. Introduction • First Observation: – Easy to solve with an extra trusted party • In most situations there is no trusted party -> This notation wouldn‘t be useful • „Purely playable games“ – No extra party which is trusted by everyone

Overview 1. Introduction 2. Solution for TM-Games 2. 1. for passive adversaries 2. 2. for malicious adversaries 3. General games 4. Summary

2. 1. Solution for TM-Games • Motivation: – Restricting the scenario to: • A special case of games (Turing-machine games) • Passive adversaries -> Easier to prove, yet useful for further proofs

2. 1. Solution for TM-Games • General Definitions: – Random Variable (RV) R: (assigns a probability to each value ) – PA = probablistic poly-time algorithm – Efficient ≙ element of PA

2. 1. Solution for TM-Games • Game network of size n: – n Turing machines with (for each TM): • • 1 read-only private input tape 1 write only private output tape 1 read/write private work tape n-1 special public communication tapes – 1 common read-only input and 1 common write only output tape

2. 1. Solution for TM-Games • A probablistic distributed algorithm S in a game network of size n is a sequence of programs • Denote the class of all such algorithms by PDA

2. 1. Solution for TM-Games • Let S∈PDA run in a network of size n with common input CI and private inputs Definition: – denotes the RV of the public history – denotes the RV of the private history of machine i

2. 1. Solution for TM-Games • Let S∈PDA run in a network of size n with common input CI and private inputs Definition: – denotes the RV of the private output of machine i – For T⊆{1, …n} let denote the vector of private histories of the members of T

2. 1. Solution for TM-Games • Indistinguishability of RV‘s: – Poly-bounded RV‘s: c constant, k∈ℕ the security parameter – Circuit is a „judge“ for two families of RV‘s U, V X a RV from U or V: – Denote by P(U, C, k) the probability that on a random sample of outputs 1

2. 1. Solution for TM-Games • Definition: (Indistinguishability of RV‘s) U and V are computationally indistinguishable if for all C, for all f∈ℕ and „sufficiently large“ k∈ℕ :

2. 1. Solution for TM-Games • Solution for a TM-Game: – An algorithm in PDA with input the following conditions are satisfied: • Agreement: for all i, j output i equals output j • Correctness: s. t.

2. 1. Solution for TM-Games • Solution for a TM-Game: – An algorithm in PDA with input the following conditions are satisfied: • Privacy: s. t.

2. 1. Solution for TM-Games • Familiy of trap-door permutations: - Easy to select an f for a k∈ℕ and some extra trap-door information - Easy to compute f(x) - Hard to compute , if one doesn‘t know the trap-door information • One-way permutation: - Same as above, but trap-door information must not exist

2. 1. Solution for TM-Games • Theorem: – If a trapdoor function exists, there exists a TMgame solver for passive adversaries • Proof sketch: – We use a lemma by Barrington‘s that simulates computation by composing elements in – > Transform our TM in a circuit and further into a straight-line program

2. 1. Solution for TM-Games • This straight-line program contains: – 0 and 1 as specially selected 5 -permutations – Variables in the range of – Instructions consist of multiplying two 5 permutations and which can be: • constant • a variable • the inverse (in ) of a variable

2. 1. Solution for TM-Games • Initialization: – Each party encodes his private input by a 5 permutation – He selects random 5 -permutations and gives the pair – He then sets to player n to player i and gives

2. 1. Solution for TM-Games • Computation with variable and: 1. case: , c constant. Then set 2. case: sets , c constant. Then each player

2. 1. Solution for TM-Games • Computation with variable and: 3. case: ⋅ , a variable. Then • assume • we can‘t just multiply as is not commutative

2. 1. Solution for TM-Games • Idea to solve the problem in case 3: – „swap“ pieces until each player can compute his share • first step: • run this for all players resulting in O(n²) swaps – Problem: privacy constraint would be violated – Solution?

2. 1. Solution for TM-Games • Random bits: - Given a trap-door permutation f A random bit of f is: - A poly-time computable function - Computing on f(x) is essentialy “as hard as inverting f” -> Blackboard

2. 1. Solution for TM-Games • Oblivious transfer (OT): – Sending information to the receiver, but it’s oblivious (“not clear”) what he received – Rabin’s OT: • A sends B an encrypted message E(m) and B can decrypt it with 50% probability -> Blackboard

2. 1. Solution for TM-Games • 1 -2 oblivious transfer: – A∈PA with input bits – B∈PA with input bit – A sends B one out of two messages, s. t. : 1. B will read , but can’t predict 2. A cannot predict

2. 1. Solution for TM-Games • Implementation of 1 -2 OT in 4 steps: 1. A selects a trapdoor permutation of size having a random bit A sends f to B and keeps secret 2. B selects at random and sends A:

2. 1. Solution for TM-Games • Implementation of 1 -2 OT in 4 steps: 3. A computes: and sends B 4. B computes

2. 1. Solution for TM-Games • Why does it work? -> Blackboard

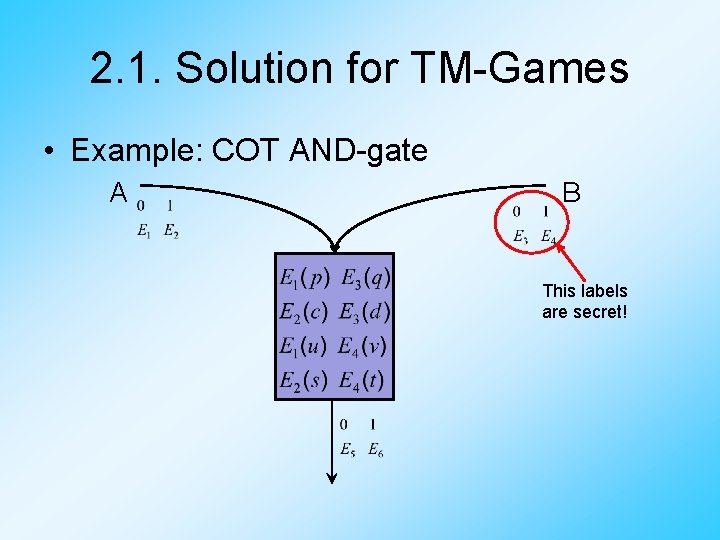
2. 1. Solution for TM-Games • Combined Oblivious Transfer (COT): – A and B owning some inputs a and b – In the end of the protocol, A has computed g(a, b), while B doesn‘t know what A has computed – When a and b are secrets, it seems that B transfered a combination of his and A‘s secret to A

2. 1. Solution for TM-Games • Example: COT AND-gate A B This labels are secret!

2. 1. Solution for TM-Games • Combined Oblivious Transfer (COT): – We‘ve seen the COT-AND gate – The COT-NOT gate is trivial -> Therefor we can compute any 2 -gates function

2. 1. Solution for TM-Games • Applying the COT to our problem: – Player 1 and n use the following function for COT: g(x, (y, z) = w , where w⋅z=y⋅x – Player 1 is A with input – Player n is B with input – Then set -> Notice that g(x, (y, ⋅)) is injective on

Overview 1. Introduction 2. Solution for TM-Games 2. 1. for passive adversaries 2. 2. for malicious adversaries 3. General games 4. Summary

2. 2. Solution for TM-Games • Motivation: – With malicious adversaries we must clarify how to handle private inputs • Say if one player stops computing or tries to pretend his private input is different from what it actually is, how can we handle this? • Theorem: – Given n players „willing to play“, less then half of which malicious, all TM-games are playable

2. 2. Solution for TM-Games • Zero-knowledge proof: Prove that you know a secret without revealing it. must satisfy 3 properties: - Completeness: - honest prover can convince honest verifier - Soundness: - cheating prover can’t convince honest verifier, except with small probability - Zero-knowledge: - no cheating verifier learns any other information

2. 2. Solution for TM-Games • What means „willing to play“? – Successfully completing a protocol s. t. : 1. For all players i, no minority can predict a bit of player i‘s input with prob. > ½ but it is guaranteed that a majority of players can efficiently compute i‘s input 2. Each player i has a sequence of random encrypted bits s. t. : 1. He knows the decryption 2. No minority can predict them 3. A majority can easily compute them

2. 2. Solution for TM-Games • How can we use this to „play“ the game? – For any randomness, players must use the bits they received – Each player proves - in zero-knowledge - that each message is what he should have send – If any player should stop at this phase then: • The others can reconstruct his random bits and private input • Compute his further messages when necessary

Overview 1. Introduction 2. Solution for TM-Games 2. 1. for passive adversaries 2. 2. for malicious adversaries 3. General games 4. Summary

3. General games • Game theory: – Definition of a general game: • A set S of possible states • A set M of possible moves • A set of knowledge functions of each state : • A payoff function p evaluating the final state

3. General games • Game theory: – Given a description of a game, how can we find some strategy satisfying some property? – Problem: given a description of a game, how can we actually PLAY the game? • For a general n-player game, we need n+1 players to play it ( which is unfortunate as we need another trusted party, which we normally don‘t have )

3. General games • Game Theory Example: – The game „poker“ is clearly playable (e. g. in our physical world) – Let NEWPOKER be the same as normal poker, but in addition you have the information, whether all hands combined form a royal flush • Is this game playable, too?

3. General games • Questions that arise: – Is there a model which makes all games playable, or at least – Does every game have a model in which it is playable? – Should we restrict us to the class of playable games?

3. General games • Theorem: – If any trap-door function exists, any game is playable if more than half of the players are honest • Idea to prove this: – Simulate a trusting party in an ideal game

Overview 1. Introduction 2. Solution for TM-Games 2. 1. for passive adversaries 2. 2. for malicious adversaries 3. General games 4. Summary

4. Summary • Theorem: – Under the assumption that any trap-door permutation exists: • We can tolerate any number of passive adversaries • We can tolerate up to ½ ⋅n malicious adversaries • If there are more than ½ ⋅n malicious adversaries then some protocols have no efficient solution

4. Summary • Why is this useful? – > Because every protocol can be formalized to a game with incomplete information – > We can even find a solution uniformly: • We can use an efficient algoritm, that, on input a protocol problem, outputs an efficient, distributed protocol for solving it

Thank you for your attention! Any questions?