4 EK 213 LINERN MODELY ter 11 00

4 EK 213 – LINEÁRNÍ MODELY Úterý 11: 00 – 12: 30 hod. učebna 212 RB © Lagová, Kalčevová © L&K

3. přednáška SIMPLEXOVÁ METODA I. © Lagová, Kalčevová © L&K

OSNOVA PŘEDNÁŠKY • • Princip simplexové metody Výchozí řešení SM Zlepšení řešení Transformace Simplexová tabulka Přírůstek účelové funkce Alternativní OŘ © L&K 3

Příklad 3. 1 • Najděte podle základní věty LP OŘ této úlohy graficky: x 1 + 2 x 2 ≤ 120 x 1 + 4 x 2 ≤ 180 (3. 1) x 1 ≤ 110 xj ≥ 0, j = 1, 2 z = 40 x 1 + 60 x 2. . . max. • Kolik bude mít soustava ekvivalentních rovnic ZŘ. . . ? © L&K 4

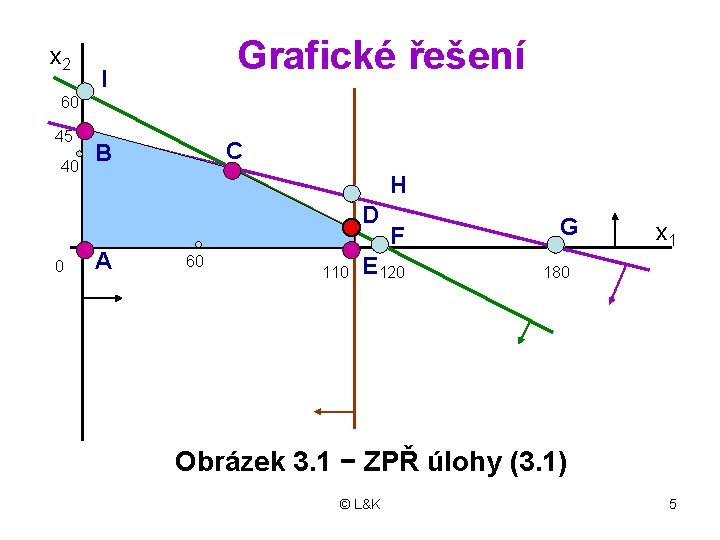
x 2 Grafické řešení I 60 45 40 C B H D 0 A 60 110 F E 120 G x 1 180 Obrázek 3. 1 − ZPŘ úlohy (3. 1) © L&K 5

• Úloha má devět ZŘ, desáté je v nekonečnu (třetí omezení je rovnoběžné s osou x 2) • Z nich pět je nezáporných • Optimálním řešením je to ZPŘ, které má nejvyšší hodnotu účelové funkce: A: x(1) = (0, 0, 120, 180, 110)T, z = 0 B: x(2) = (0, 45, 30, 0, 110)T, z = 2700 C: x(3) = (60, 30, 0, 0, 50)T, z = 4200 D: x(4) = (110, 5, 0, 50, 0)T, z = 4700 E: x(5) = (110, 0, 10, 70, 0)T, z = 4400. © L&K 6

SIMPLEXOVÁ METODA • Jak jsme viděli, je možno OŘ úlohy LP nalézt mezi základními přípustnými řešeními • V praxi však vzniká zásadní problém, kterým je počet ZPŘ • S rostoucím m a n roste horní hranice počtu ZPŘ velice rychle • Např. pro n = 10, m = 5 je to 252 n = 100, m = 10 je větší než bilión n = 1000, m = 400 je to 5. 10290 © L&K 7

• Je však možné využít základní větu LP efektivněji • Není třeba počítat všechna ZŘ, ale vhodně z nich vybírat: − pouze základní přípustná řešení − z nich vybírat jen ta, která jsou vzhledem k hledanému extrému „perspektivní“ • Znamená to vlastně sledovat „cestu“, která vede přes základní přípustná řešení k základnímu optimálnímu řešení © L&K 8

• Metodu odvodil a její konečnost dokázal v padesátých letech 20. století americký vědec německého původu George Bernard Dantzig • Podle její grafické interpretace ji nazval simplexová metoda (SM) • Konvexní obal n +1 bodů (n bodů a počátek) je nazýván n-rozměrný simplex • Je to tedy konvexní množina, která má počátek a konečný počet krajních bodů © L&K 9

PRINCIP SM • • • Najdeme jedno ze ZPŘ úlohy LP, které považujeme za výchozí řešení (VŘ) iteračního postupu Přejdeme k dalšímu ZPŘ, které má lepší hodnotu účelové funkce (v krajním případě stejnou) V konečném počtu kroků dojdeme buď: − k optimálnímu řešení − nebo k závěru, že OŘ neexistuje © L&K 10

VÝCHOZÍ ŘEŠENÍ SM • Teoreticky může být výchozím řešením libovolné ZŘ soustavy ekvivalentních rovnic v (2. 14), které splňuje i podmínky nezápornosti • Náhodným výběrem je však obtížné zajistit nezápornost libovolného ZŘ • Zvolíme např. v (2. 13) náhodně: x 2 = 0, x 4 = 0 © L&K 11

x 1 + 2 x 2 + x 3 = 120 x 1 + 4 x 2 + x 4 = 180 x 1 − x 2 − x 5 = 90 x 1 + x 6 = 110 • Dosadíme x 2 = 0, x 4 = 0 • Základním řešením je vektor. . . . ? x = (180, 0, -60, 0, 90, -70)T • Vidíme, že toto ZŘ soustavy rovnic je nepřípustné © L&K 12

JEDNOFÁZOVÁ SM • Nejjednodušší je nalezení výchozího řešení v soustavě vlastních omezení, která obsahuje pouze nerovnice typu ≤ • Ke každé nerovnici ≤ přičteme přídatnou proměnnou • Přídatné proměnné mají jednotkový vektor koeficientů • Dostaneme tak soustavu rovnic v kanonickém tvaru. . . . . ? © L&K 13

• Položíme-li všechny strukturní proměnné rovny nule, je přídatná proměnná rovna pravé straně svého omezení • Výchozím řešením je tedy vektor x(1) = (0, 0, . . . , 0, b 1, . . . , bm ) (3. 2) • Toto řešení má maximálně* m kladných složek (základní proměnné), tj. minimálně n složek nulových (nezákladní proměnné) • Podle definice je to tedy ZPŘ © L&K 14

Příklad 3. 2 • Vypočtěte výchozí řešení úlohy (3. 1) 1. Nerovnice vyrovnáme na rovnice: x 1 + 2 x 2 + x 3 = 120 x 1 + 4 x 2 + x 4 = 180 (3. 3) x 1 + x 5 = 110 xj ≥ 0, j = 1, 2, …, 5 • Dosadíme nulové hodnoty strukturních proměnných x 1= 0, x 2 = 0 • Vypočteme x 3 = 120, x 4 = 180 x 5 = 110 © L&K 15

• Proměnné x 3, x 4 a x 5 jsou základní proměnné (bázické) • Hodnota základní proměnné je rovna pravé straně omezení • Proměnné x 1, x 2 jsou nezákladní (nebázické) • Hodnota nezákladní proměnné je rovna nule • Vektor x(1) = (0, 0, 120, 180, 110)T (3. 4) je výchozím řešením SM © L&K 16

2. Upravíme účelovou funkci tak, aby všechny proměnné byly na levé straně, tj. anulujeme ji: z - 40 x 1 - 60 x 2 = 0 (3. 5) • Dostáváme MM v kanonickém tvaru: • x 1 + 2 x 2 + x 3 = 120 x 1 + 4 x 2 + x 4 = 180 x 1 + x 5 = 110 - 40 x 1 - 60 x 2 +z = 0 xj ≥ 0, j = 1, 2, …, 5 © L&K 17

• Čtvrtou základní proměnnou je zde z • Má zvláštní postavení, zůstává základní proměnnou po celou dobu výpočtu • Výchozí hodnota účelové funkce je z(1) = 0 • Výchozí řešení můžeme zapsat včetně této hodnoty: x(1) = (0, 0, 120, 180, 110, 0) • Grafickým znázorněním výchozího řešení je bod se souřadnicemi [0, 0], tj. počátek © L&K 18

ITERAČNÍ POSTUP • Po získání výchozího řešení začíná opakování iterací SM • Každá iterace SM má tři části: 1. test optima 2. zlepšení řešení 3. transformace • Podle základní věty LP končí iterační postup v konečném počtu kroků nalezením OŘ nebo zjištěním, že neexistuje © L&K 19

1. TEST OPTIMA • Položíme si otázku: Co se stane s hodnotou účelové funkce, jestliže nulovou hodnotu některé nezákladní proměnné zvýšíme? • Vyjdeme z výchozího řešení (3. 4): x(1) = (0, 0, 120, 180, 110)T • Položíme x 1=1 a dosadíme do anulované účelové funkce (3. 5): z − 40 x 1 = 0, tj. z = 0+40. 1=40 • Zvýší-li se hodnota proměnné x 1 o jednotku, vzroste hodnota© L&K z o 40 20

• Položme nyní x 2 =1. Po dosazení je z − 60 x 2 = 0, tj. z = 60 • S růstem proměnné x 2 o jednotku vzroste hodnota z o 60 • Je-li u nezákladní proměnné v anulované účelové funkci záporný koeficient, s růstem hodnoty této proměnné hodnota účelové funkce z vzroste • Absolutní hodnota tohoto koeficientu ukazuje velikost přírůstku funkce z na jednu jednotku proměnné xj © L&K 21

2. ZLEPŠENÍ ŘEŠENÍ • Zvolíme některou nezákladní proměnnou se záporným koeficientem v účelové funkci (3. 5): z - 40 x 1 - 60 x 2 = 0 • Je-li v účelové funkci více záporných koeficientů, volíme obvykle ten, který znamená nejvyšší přírůstek účelové funkce na jednotku proměnné, tj. nejmenší koeficient • Podle koeficientů v řádce z je v absolutní hodnotě (tj. nejmenší) vyšší druhý, zvolíme tedy x 2 © L&K 22

• Tato proměnná bude mít v další iteraci kladnou hodnotu (označíme ji obecně t) • V omezeních (3. 4) dosadíme x 2 = t > 0 : x 1 + 2 t + x 3 = 120 x 1 + 4 t + x 4 = 180 (3. 6) x 1 + x 5 = 110 • Dosadíme x 1 = 0 a vypočteme hodnoty základních proměnných: x 3 = x 4 = (3. 7) x 5 = © L&K 23

• Z podmínek nezápornosti vyplývá: x 3 = 120 − 2 t ≥ 0 x 4 = 180 − 4 t ≥ 0 (3. 8) x 5 = 110 − 0 t ≥ 0 Odtud je. . . ? • Zvolíme nejvyšší možnou hodnotu t: t = min (60, 45) = 45 (3. 9) © L&K 24

• Dosadíme do (3. 8) a vypočteme nové hodnoty základních proměnných. . . . ? x 3 = x 4 = x 5 = • Vidíme, že proměnná x 4 se vynulovala, proměnné s kladnou hodnotou jsou opět tři: x(2) = (0, 45, 30, 0, 110)T • Vektor x(2) je tedy ZPŘ © L&K 25

• Co se stane, jestliže hodnotu nové základní proměnné nezvolíme podle (3. 9)? a. Zvolíme nejdříve t < 45 např. pro t = 30 je z (3. 8) nové řešení. . . ? • Je to PŘ. . . ? • Je to ZPŘ. . . ? © L&K 26

b. Zvolíme nyní t > 45 např. pro t = 50 je nové řešení. . . ? • Je to ZPŘ. . . ? • Graficky odpovídá výměně základní proměnné a nezákladní proměnné přechod od jednoho vrcholu konvexního polyedru ke druhému © L&K 27

3. TRANSFORMACE ŘEŠENÍ • Novou základní proměnnou nazveme vstupující proměnná • Proměnnou, jejíž hodnota se vynulovala nazveme vystupující proměnná • Vstupující proměnná je v další iteraci základní, musí proto mít jednotkový vektor koeficientů • Soustavu omezení i účelovou funkci budeme transformovat Gaussovou metodou úplné eliminace • Výpočet uspořádáme do tabulky © L&K 28

SIMPLEXOVÁ TABULKA • Řádky tabulky (ST) odpovídají vlastním omezením • V posledním řádku je účelová funkce • Sloupce tabulky odpovídají vektorům koeficientů strukturních a přídatných proměnných • Pravé strany vlastních omezení jsou posledním sloupcem tabulky • V prvním sloupci jsou základní proměnné © L&K 29 dané iterace

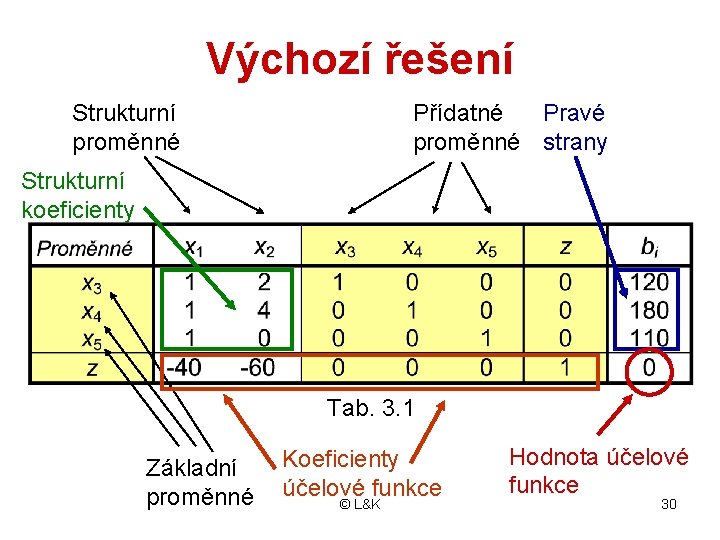
Výchozí řešení Strukturní proměnné Přídatné Pravé proměnné strany Strukturní koeficienty Tab. 3. 1 Základní proměnné Koeficienty účelové funkce © L&K Hodnota účelové funkce 30

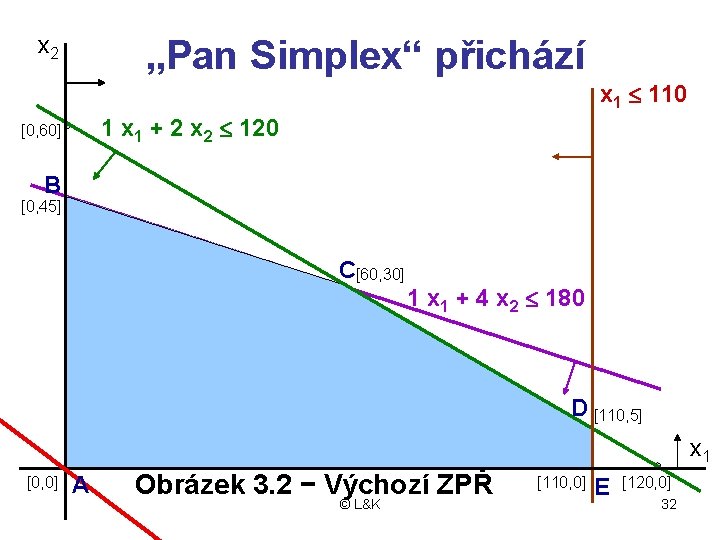
• Ze simplexové tabulky přečteme ZPŘ: − hodnoty základních proměnných jsou rovny pravým stranám − nezákladní proměnné jsou rovny nule • V tabulce 3. 1 jsou základní proměnné: x 3 = 120, x 4 = 180, x 5 = 120 • Nezákladní proměnné jsou: x 1 = 0, x 2 = 0 • Vektor výchozího řešení je: x(1)=(0, 0, 120, 180, 120), z(1)=0 • Grafickým znázorněním je bod A © L&K 31

x 2 „Pan Simplex“ přichází x 1 £ 110 1 x 1 + 2 x 2 £ 120 [0, 60] B [0, 45] C[60, 30] 1 x 1 + 4 x 2 £ 180 D [110, 5] x 1 [0, 0] A Obrázek 3. 2 − Výchozí ZPŘ © L&K [110, 0] E [120, 0] 32

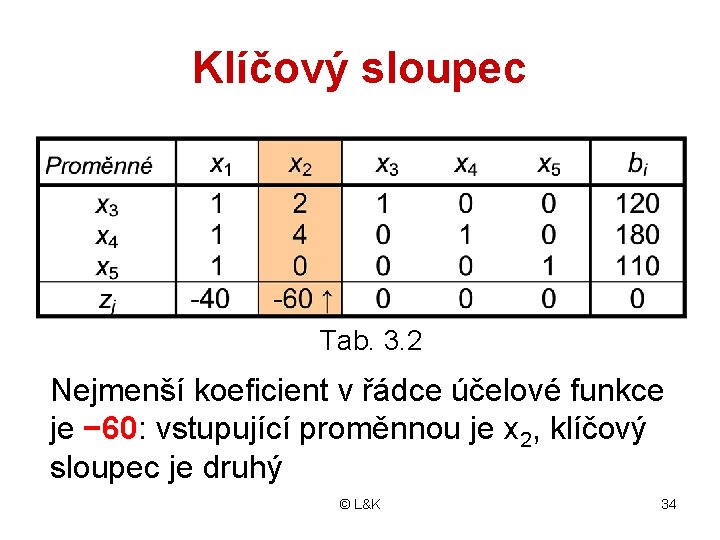
1. Test optima a určení vstupující proměnné • Najdeme nejmenší koeficient v řádce z: a. je-li nezáporný, není možno zvýšit hodnotu účelové funkce: → OŘ b. je-li záporný, nalezli jsme proměnnou, která zlepší hodnotu účelové funkce: → vstupující proměnná • Sloupec této proměnné označíme jako klíčový sloupec © L&K 33

Klíčový sloupec Tab. 3. 2 Nejmenší koeficient v řádce účelové funkce je − 60: vstupující proměnnou je x 2, klíčový sloupec je druhý © L&K 34

2. Určení vystupující proměnné • Tabulku rozšíříme o další sloupec, který označíme symbolem t • Vypočteme podíly pravých stran bi a kladných koeficientů klíčového sloupce a zapíšeme do sloupce t • Najdeme nejmenší z vypočtených podílů • Určíme tak vystupující proměnnou a klíčový řádek © L&K 35

Klíčový řádek Tab. 3. 3 • x 3 = 120 − 2. t ≥ 0 → t =120/2 = 60 • x 4 = 180 − 4. t ≥ 0 → t = 180/4 = 45 • Pro x 5 hodnotu t neurčujeme • Vystupující proměnnou je x 4, klíčový řá© L&K dek je druhý 36

Klíčový prvek Tab. 3. 4 Na průsečíku klíčového sloupce a klíčového řádku leží klíčový prvek Tabulku transformujeme metodou úplné eliminace tak, aby v klíčovém sloupci byl jednotkový vektor s jedničkou na místě klíčového prvku © L&K 37

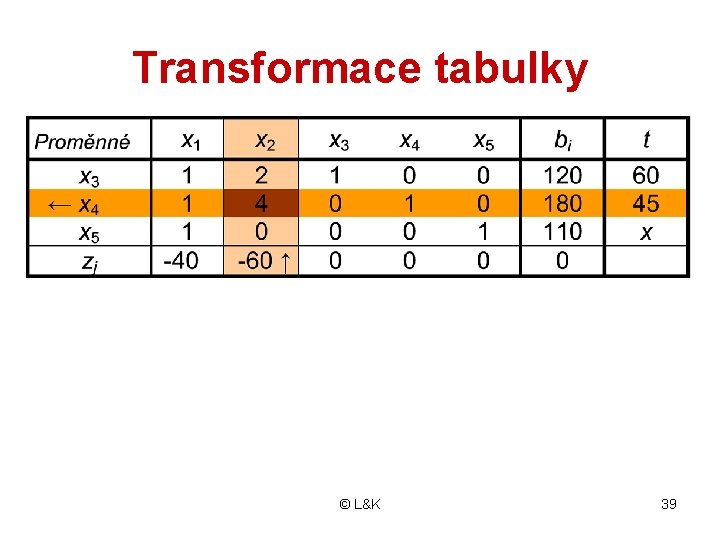
3. TRANSFORMACE ŘEŠENÍ 1. V klíčovém řádku zapíšeme proměnnou x 2 2. Klíčový řádek dělíme 4 3. Násobíme ho (-2) a připočteme k 1. řádku 4. Třetí řádek opíšeme 5. Klíčový řádek násobíme (-60) a přičteme k účelové funkci • Novým řešením je vektor x(2)=(0, 45, 30, 0, 110), z(2)=2700 • Grafickým znázorněním je bod B © L&K 38

Transformace tabulky Proměnné x 3 x 2 x 5 zj x 1 x 2 x 3 x 4 x 5 1/2 1/4 1 -25 0 1 0 0 0 -1/2 1/4 0 15 0 0 1 0 Tab. 3. 5 © L&K i 30 45 110 2700 (+60) (-2) 39

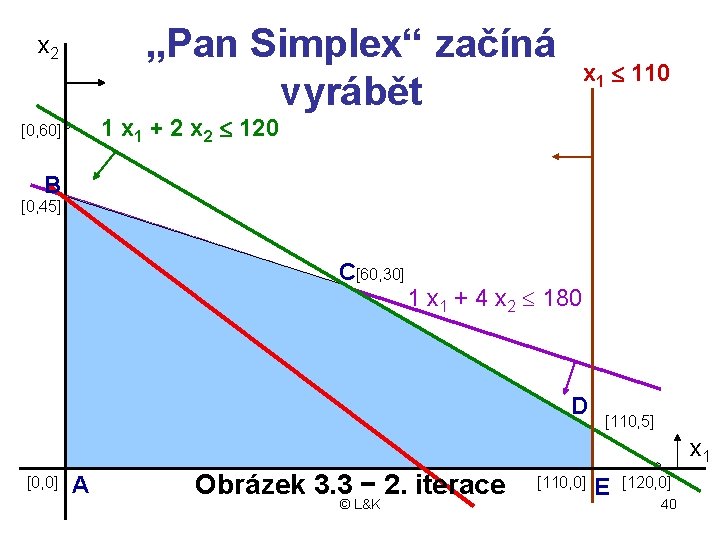
„Pan Simplex“ začíná vyrábět x 2 x 1 £ 110 1 x 1 + 2 x 2 £ 120 [0, 60] B [0, 45] C[60, 30] 1 x 1 + 4 x 2 £ 180 D [110, 5] x 1 [0, 0] A Obrázek 3. 3 − 2. iterace © L&K [110, 0] E [120, 0] 40

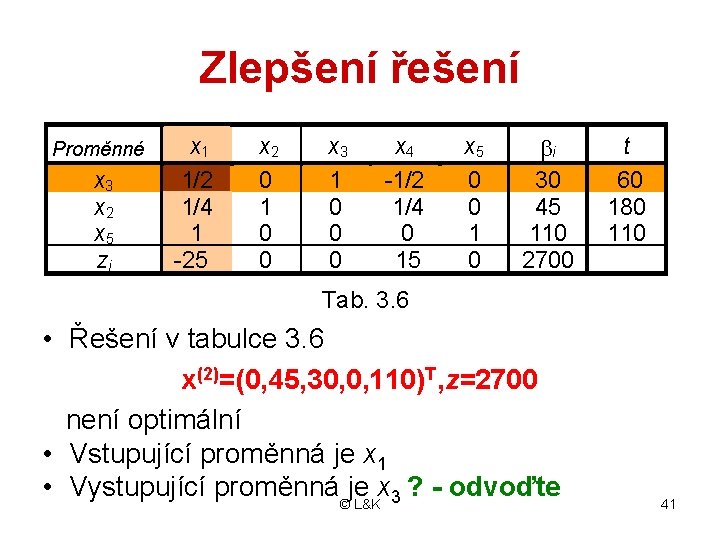
Zlepšení řešení Proměnné x 3 x 2 x 5 zj x 1 1/2 1/4 1 -25 x 2 0 1 0 0 x 3 1 0 0 0 x 4 -1/2 1/4 0 15 x 5 0 0 1 0 i 30 45 110 2700 t 60 180 110 Tab. 3. 6 • Řešení v tabulce 3. 6 x(2)=(0, 45, 30, 0, 110)T, z=2700 není optimální • Vstupující proměnná je x 1 • Vystupující proměnná©je x ? - odvoďte L&K 3 41

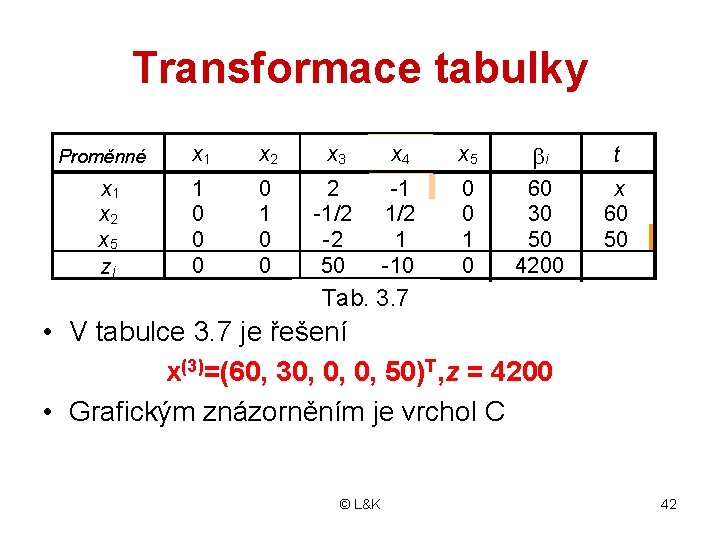
Transformace tabulky Proměnné x 1 x 2 x 5 zj x 1 x 2 x 3 x 4 x 5 i t 1 0 0 2 -1/2 -2 50 -1 1/2 1 -10 0 0 1 0 60 30 50 4200 x 60 50 Tab. 2. 9 3. 7 • V tabulce 3. 7 je řešení x(3)=(60, 30, 0, 0, 50)T, z = 4200 • Grafickým znázorněním je vrchol C © L&K 42

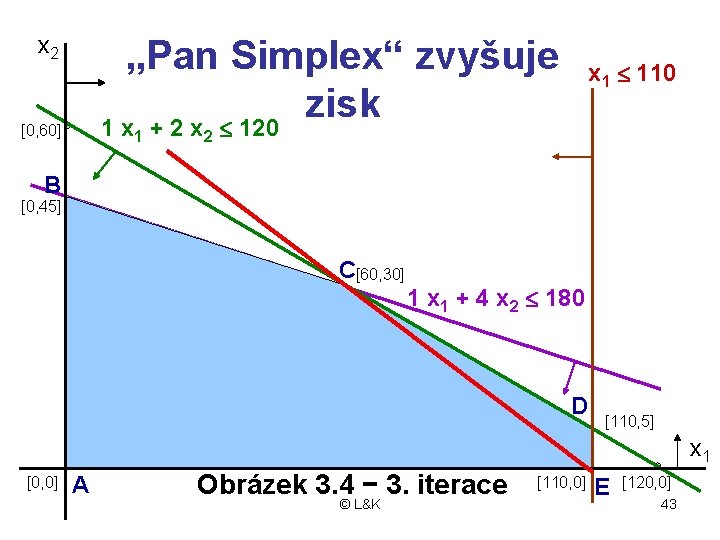
x 2 „Pan Simplex“ zvyšuje zisk 1 x + 2 x £ 120 [0, 60] 1 x 1 £ 110 2 B [0, 45] C[60, 30] 1 x 1 + 4 x 2 £ 180 D [110, 5] x 1 [0, 0] A Obrázek 3. 4 − 3. iterace © L&K [110, 0] E [120, 0] 43

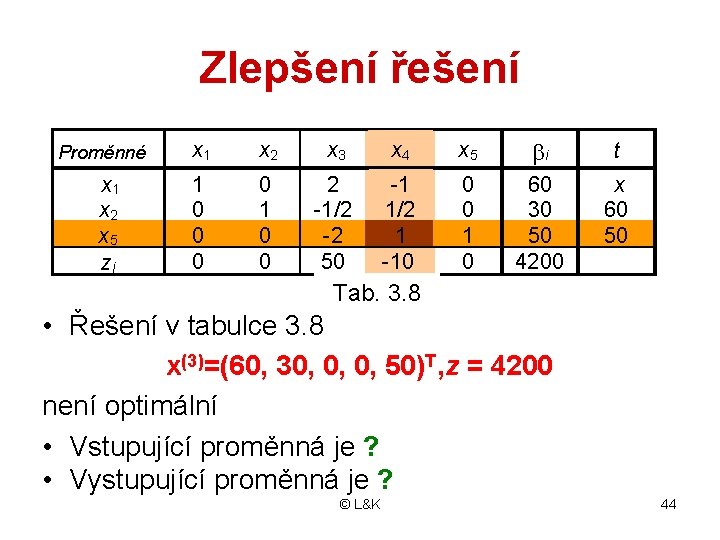
Zlepšení řešení Proměnné x 1 x 2 x 5 zj x 1 x 2 x 3 x 4 x 5 i t 1 0 0 2 -1/2 -2 50 -1 1/2 1 -10 0 0 1 0 60 30 50 4200 x 60 50 Tab. 2. 9 3. 8 • Řešení v tabulce 3. 8 x(3)=(60, 30, 0, 0, 50)T, z = 4200 není optimální • Vstupující proměnná je ? • Vystupující proměnná je ? © L&K 44

Transformace tabulky 50 Tab. 2. 10 3. 9 • Test optima: v řádce účelové funkce není žádný záporný koeficient. Řešení v tabulce 3. 9 je optimální: x(4) = (110, 5, 0, 50, 0)T, z = 4700. • Grafickým znázorněním je bod D © L&K 45

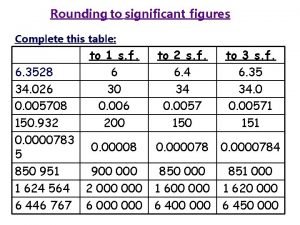
x 2 1 x 1 [0, 60] „Pan Simplex“ nachází x optimum + 2 x £ 120 1 £ 110 2 B [0, 45] C[60, 30] 1 x 1 + 4 x 2 £ 180 D OPTIMUM [0, 0] A Obrázek 3. 6 − OŘ © L&K [110, 0] [110, 5] x 1 E [120, 0] 46

Ekonomická interpretace OŘ • V (3. 1) jsme z úlohy LP v příkladu 1. 1 vynechali třetí omezení, ostatní interpretace se nemění • Z tab. 3. 9 přečteme vektor OŘ: x (4) = (110, 5, 0, 50, 0)T, z = 4700 • Firma bude vyrábět 110 krabiček šroubků a 5 krabiček matic • Čas lisu je celý využit, balicí linka má 50 minut volných, počet KŠ je přesně 110 • Maximální zisk je 4700 Kč © L&K 47

Verifikace OŘ • Všechny podmínky modelu jsou splněny: 1. Spotřeba času lisu nepřekročí 120 min. 2. Balení spotřebuje jen 130 min. 3. Počet krabiček šroubků dosáhne horní hranice 110 © L&K 48

PŘÍRŮSTEK z • Rozdíl mezi novou a původní hodnotou účelové funkce: ∆z = − zj. t (3. 10) je absolutní přírůstek* účelové funkce • Je dán součinem dvou veličin: – jednotkovým přírůstkem účelové funkce ( koeficient zj * (násobený -1)) – maximální možnou velikostí vstupující proměnné (t) © L&K 49

Příklad 3. 3 • Zopakujeme: V tabulce 3. 2 jsme vybrali v první iteraci vstupující proměnnou x 2 : • Absolutní přírůstek účelové funkce je © L&K ? 50

• Přírůstek účelové funkce přinese i proměnná x 1 • Jednotkový přírůstek je. . . ? • Proměnná x 1 může nabýt hodnoty ? • Celkový přírůstek účelové funkce je ? • Vidíme, že proměnná x 1 přinese větší přírůstek účelové funkce © L&K 51

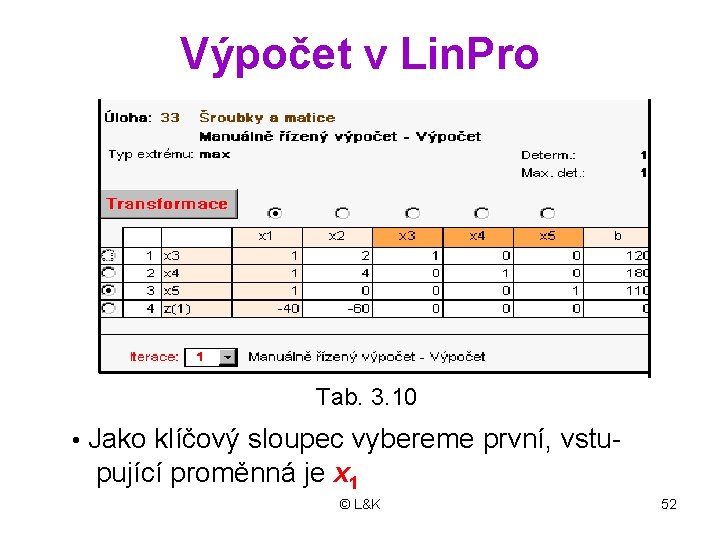
Výpočet v Lin. Pro Tab. 3. 10 • Jako klíčový sloupec vybereme první, vstu- pující proměnná je x 1 © L&K 52

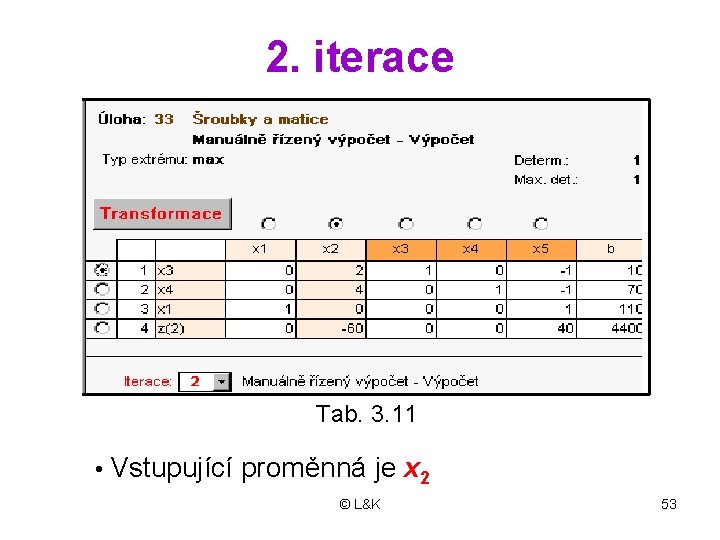
2. iterace Tab. 3. 11 • Vstupující proměnná je x 2 © L&K 53

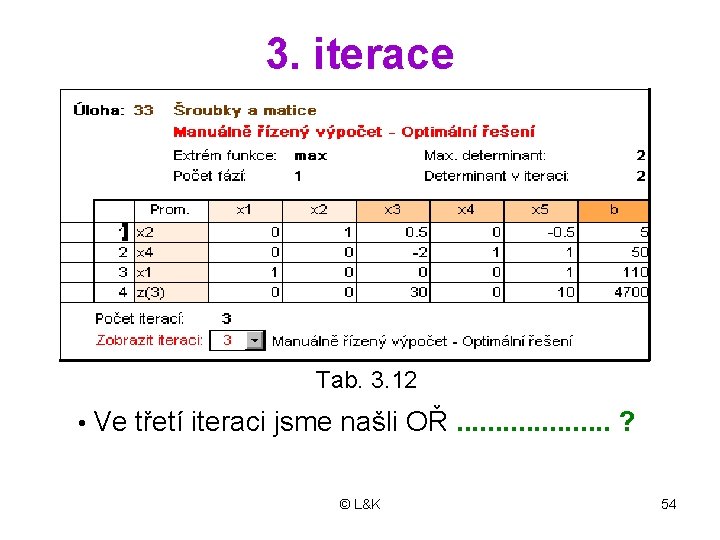
3. iterace Tab. 3. 12 • Ve třetí iteraci jsme našli OŘ. . . . . ? © L&K 54

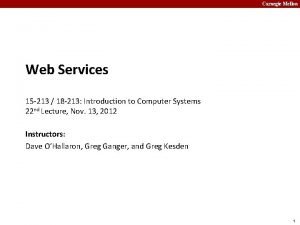
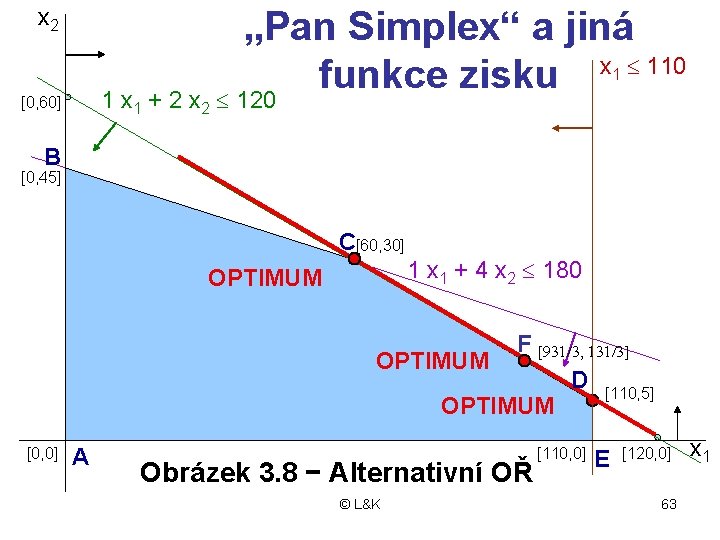
x 2 [0, 60] 1 x 1 + 2 x 2 „Pan Simplex“ jde £ 120 jinudy x 1 £ 110 B [0, 45] C[60, 30] 1 x 1 + 4 x 2 £ 180 D OPTIMUM A [0, 0] Obrázek 3. 7 − „Jiná cesta“ © L&K [110, 0] [110, 5] E [120, 0] 55 x 1

ALTERNATIVNÍ OŘ • Jakou hodnotu má koeficient zj u nezákladní proměnné xj v OŘ*. . . ? a. zj > 0: s růstem hodnoty xj se hodnota z sníží b. zj = 0: s růstem hodnoty xj se hodnota z nezmění - zvolíme-li proměnnou xj jako vstupující, dostaneme v další iteraci jiné OŘ - tzv. alternativní OŘ © L&K 56

• Nové OŘ má stejnou hodnotu účelové funkce • Má ale jiné základní proměnné • Víme, že v tomto případě je OŘ nekonečně mnoho • Jak je vypočteme. . . . ? • Takto vypočtené OŘ není základní, pouze přípustné © L&K 57

Příklad 3. 4 • Uvažujme kapacitní problém (3. 1) x 1 + 2 x 2 ≤ 120 x 1 + 4 x 2 ≤ 180 x 1 ≤ 110 xj ≥ 0, j = 1, 2 s novou účelovou funkcí* z = 40 x 1+ 80 x 2. . . max. • Simplexovou metodou vypočteme OŘ © L&K 58

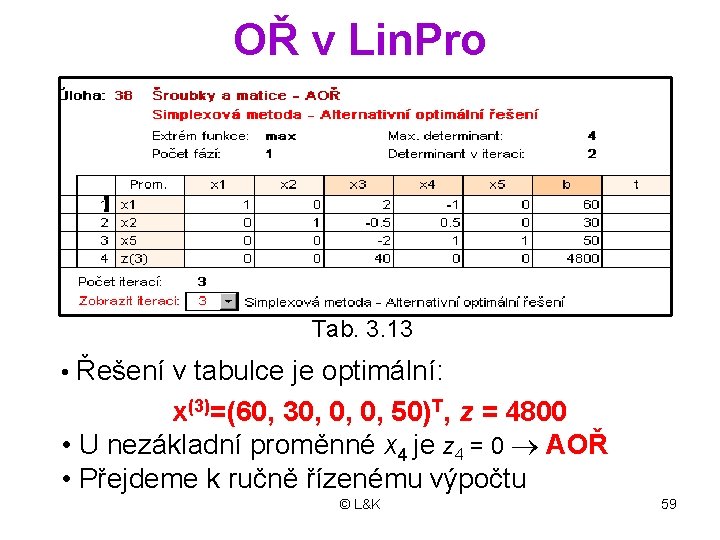
OŘ v Lin. Pro Tab. 3. 13 • Řešení v tabulce je optimální: x(3)=(60, 30, 0, 0, 50)T, z = 4800 • U nezákladní proměnné x 4 je z 4 = 0 AOŘ • Přejdeme k ručně řízenému výpočtu © L&K 59

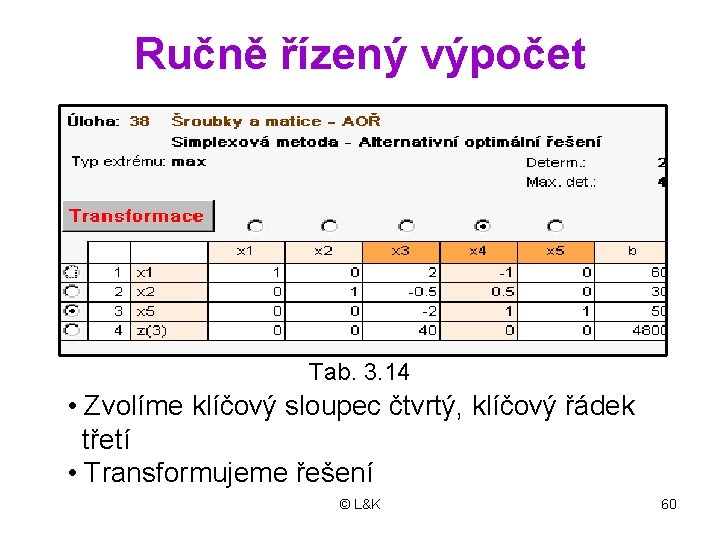
Ručně řízený výpočet Tab. 3. 14 • Zvolíme klíčový sloupec čtvrtý, klíčový řádek třetí • Transformujeme řešení © L&K 60

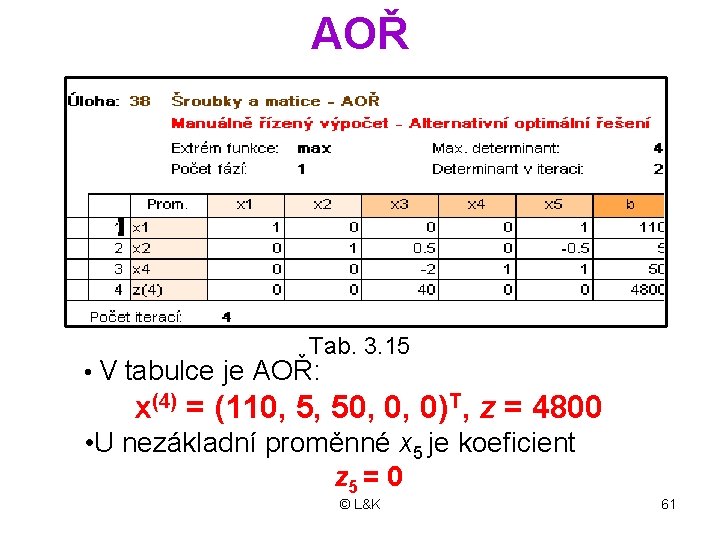
AOŘ Tab. 3. 15 • V tabulce je AOŘ: x(4) = (110, 5, 50, 0, 0)T, z = 4800 • U nezákladní proměnné x 5 je koeficient z 5 = 0 © L&K 61

• Optimálním řešením je i každá konvexní kombinace dosud vypočtených OŘ • Např. : x(5)= 1/3 x(3) + 2/3 x(4) = = 1/3 (60, 30, 0, 0, 50)T + + 2/3 (110, 5, 0, 50, 0)T = = (93 1/3, 13 1/3, 0, 33 1/3, 16 2/3) z(5)= 93 1/3. 40 + 13 1/3. 80 = 4800 • Je toto OŘ základní. . . . ? © L&K 62

x 2 „Pan Simplex“ a jiná x £ 110 funkce zisku £ 120 1 1 x 1 + 2 x 2 [0, 60] B [0, 45] C[60, 30] OPTIMUM 1 x 1 + 4 x 2 £ 180 F [931/3, 131/3] OPTIMUM D [110, 5] OPTIMUM [0, 0] A Obrázek 3. 8 − Alternativní OŘ © L&K [110, 0] E [120, 0] 63 x 1

KONEC © L&K 64