4 EK 213 LINERN MODELY ter 11 00

4 EK 213 – LINEÁRNÍ MODELY Úterý 11: 00 – 12: 30 hod. učebna 212 RB © Lagová, Kalčevová © L&K

8. PŘEDNÁŠKA DOPRAVNÍ PROBLÉM I. © L&K 2

OSNOVA PŘEDNÁŠKY • Distribuční problémy • Matematický model dopravního problé mu • Duální problém k dopravnímu problému • Výchozí řešení: metoda SZR indexní metoda VAM • Nevyrovnaný dopravní problém © L&K 3

DISTRIBUČNÍ PROBLÉMY • Speciální úlohy LP, které se zabývají distribucí určité homogenní komodity - např. rozvoz zboží, rozdělení práce, přidělení pracovníků, strojů apod. , např. : - obecný distribuční problém - přiřazovací problém - kontejnerový problém - okružní dopravní problém - úloha o pokrytí - výrobně-přepravní problém atd. © L&K 4

• Liší se od úloh LP, které jsme dosud probírali, svým specifickým matematickým modelem • Řada z nich je charakteristická požadavkem celočíselnosti proměnných • Řeší se proto specifickými metodami • Nejjednodušším reprezentantem je dopravní problém (DP) © L&K 5

DOPRAVNÍ PROBLÉM • Řeší distribuci homogenní látky od dodavatelů k odběratelům • Je dáno: − počet dodavatelů m − počet odběratelů n − kapacity dodavatelů ai, − požadavky odběratelů bj − „cena“ (náklady, vzdálenost atd. ) za do dání jedné jednotky cij • Kapacity dodavatelů jsou zadány ve stejných jednotkách jako požadavky odběratelů © L&K 6

• Úkol: určit kolik jednotek dodá každý dodavatel každému odběrateli • Cíl: uspokojit požadavky odběratelů tak, aby hodnota stanoveného cíle byla minimální © L&K 7

FORMULACE MM • Proměnná xij v dopravním problému (DP) určuje množství homogenní látky dodané i-tým dodavatelem j-tému odběrateli • Počet proměnných DP je m. n • Předpokládá se rovnost součtu kapacit a součtu požadavků (vyrovnaný DP)* • Omezení jsou proto formulována v rovnicích • Počet omezení DP je m+n © L&K 8

• Prvních m omezení zajišťuje kapacitu dodavatelů (řádková omezení): xi 1 + xi 2 +. . . + xin = ai , (8. 1) i =1, 2, . . . , m • Další omezení zajistí splnění požadavků odběratelů (sloupcová omezení): x 1 i + x 2 i +. . . + xmi = bj , (8. 2) j = 1, 2, . . . , n © L&K 9

• Podmínky nezápornosti: xii ≥ 0, (8. 3) i =1, 2, . . . , m j =1, 2, . . . , n • Účelovou funkci minimalizujeme: z = c 11 x 11 + c 12 x 12 +. . . + cmnxmn (8. 4) • Je možno řešit DP s maximalizační účelovou funkcí. . . . . ? © L&K 10

Obecná formulace DP Na množině omezení (8. 5) xij ≥ 0, i = 1, 2, . . . , m, j = 1, 2, . . . , n minimalizovat účelovou funkci © L&K 11

Příklad 8. 1 • Firma Kámen těží ve třech lomech štěrkopísek • Štěrkopísek dodává na tři velké stavby • Kapacita lomů je 150, 200 a 250 tun • Požadavky staveb jsou 220, 200 a 180 tun • Vzdálenosti jednotlivých lomů od staveb v km jsou uvedeny v tabulce 8. 1 • Určete objem dodávek z jednotlivých lomů na stavby tak, aby počet ujetých tunokilometrů byl minimální © L&K 12

1. Volba proměnných • • • Proměnné označíme xij Hodnota proměnné xij určuje množství štěrkopísku v tunách dodané i−tým lomem j−tému odběrateli (stavbě) Proměnných je m. n = 9 Vektor proměnných má složky x = (x 11, x 12, x 13, x 21, x 22, x 23, x 31, x 32, x 33) Na obrázku 8. 1 je znázorněna volba náhodně zvolené proměnné x 32 © L&K 13

Volba proměnné Tab. 8. 1 Vzdálenosti v km Obr. 8. 1 © L&K 14

Matematický model • x 11 + x 12 + x 13 • x 11 x 12 = 150 x 21 + x 22 + x 23 = 200 x 31 + x 32 + x 33 = 250 + x 21 + x 31 = 220 + x 22 + x 32 = 200 x 13 + x 23 + x 33 = 220 xij ≥ • i = 1, 2, 3, j = 1, 2, 3 • 9 x 11 + 3 x 12 + . . . + 11 x 33 = © L&K 0 (8. 6) z 15

ZVLÁŠTNOSTI MM 1. Matice strukturních koeficientů A se skládá pouze z nul a jedniček 2. Vektor strukturních koeficientů proměnné xij má jedničku na i-tém a j+m-tém místě, ostatní prvky jsou rovny nule 3. Ve vyrovnaném DP je vždy jedno vlastní omezení lineární kombinací ostatních 1. Hodnost rozšířené matice [ A│b ] vyrovnaného DP je m+n-1 4. Všechny proměnné, kapacity i požadavky jsou ve stejných jednotkách © L&K 16

Příklad 8. 2 • Vypište rozšířenou matici [ A│b ] z úlohy (8. 6) a vypočtěte její hodnost (8. 7) [ A│b ] = © L&K 17

Hodnost matice [ A│b ] • Upravená matice [ A│b ] : [ A│b ] = • Poslední řádek se vynuloval • Hodnost h([ A│b ] ) = 5 © L&K 18

VLASTNOSTI DP • Definice 1: Přípustné řešení DP je vektor x = (x 11, x 12, . . . , xmn)T, jehož složky vyhovují všem omezením • Věta (1): • DP má přípustné řešení: - položíme xij = ai. bj / K kde K=∑ ai = ∑ bj , i= 1, 2, . . . , m, j= 1, 2, . . . , n © L&K 19

• Dosadíme do řádkového omezení (8. 1): • Upravíme (vytkneme ai / K) • Srovnáním s (8. 1) vidíme, že omezení jsou splněna • Totéž platí pro sloupcová omezení (8. 2) © L&K 20

• Definice 2: Základní přípustné řešení DP je přípustné řešení, které má nejvýše (m+n− 1) kladných složek. Vektory strukturních koeficientů u kladných složek tvoří lineárně nezávislou soustavu • Věta (2): • DP má základní přípustné řešení: - dosadíme vždy xrs = min (ar, bs) (Tím vyškrtneme vždy jeden řádek nebo sloupec, nakonec dva – viz příklad) © L&K 21

• Definice 3: Optimální řešení je přípustné řešení, které minimalizuje účelovou funkci • Věta (3): • DP má optimální řešení: - množina přípustných řešení tvoří kon vexní polyedr (je omezena kapacitami, požadavky a podmínkami nezápornosti) © L&K 22

DUÁLNÍ PROBLÉM K DP • Duální proměnné přiřazené řádkovým omezením označíme ui • Duální proměnné odpovídající sloupcovým omezením nazveme vj • Počet duálních proměnných je m+n • Počet vlastních omezení je m. n • Vlastní omezení jsou nerovnice typu ≤ • Účelovou funkci maximalizujeme © L&K 23

OBECNÝ MODEL • Za podmínek + ≤ i=1, 2, . . . , m, j=1, 2, . . . , n maximalizovat účelovou funkci (8. 8) + (8. 9) • Protože jde o nesymetrický duální problém, nemají duální proměnné podmínky nezápornosti © L&K 24

Příklad 8. 3 • Formulujte duální problém k dopravnímu problému (8. 6) • Duální problém má: ~ 6 proměnných u. T=(u 1, u 2, u 3, v 1, v 2, v 3 ) ~ 9 omezení ve tvaru nerovnic typu ≤ • Duální proměnné nemají podmínku nezápornosti • Účelovou funkci maximalizujeme © L&K 25

Primární problém x 11 + x 12 + x 13 x 11 x 12 = 150 x 21 + x 22 + x 23 = 200 x 31 + x 32 + x 33 = 250 + x 21 + x 31 = 220 + x 22 + x 32 = 200 x 13 + x 23 + x 33 = 220 xij ≥ u 1 u 2 u 3 v 1 v 2 v 3 0 i = 1, 2, 3, j = 1, 2, 3 9 x 11 + 3 x 12 +. . . . © L&K + 11 x 33 = z ? Formulujte 26

Duální problém • Za podmínek u 1 u 1 u 2 u 2 + v 1 ≤ + v 2 ≤ + v 3 ≤ u 3 + v 1 ≤ u 3 + v 2 ≤ u 3 + v 3 ≤ 9 3 2 7 8 4 5 6 11 • maximalizovat f = 150 u 1+200 u 2 +250 u 3 +220 v 1+200 v 2 +180 v 3 © L&K 27

DOPRAVNÍ TABULKA • Řádek tabulky odpovídá řádkovému omezení (8. 1) • Sloupec odpovídá sloupcovému omezení (8. 2) • Řádky a sloupce vymezují políčka • Políčko tabulky odpovídá jedné dopravní cestě mezi dodavatelem a odběratelem, tj. jedné proměnné xij © L&K 28

Příklad 8. 4 • Uspořádejte dopravní problém z příkladu 8. 1 do dopravní tabulky • Sečteme kapacity: 150+200+250=600 • Sečteme požadavky: 220+200+180=600 • Dopravní problém je vyrovnaný © L&K 29

Dopravní tabulka O 1 D 2 D 3 bj O 2 O 3 9 3 2 7 8 4 5 6 11 220 200 ai 150 200 180 250 600 Tab. 8. 2 © L&K 30

VÝCHOZÍ ŘEŠENÍ DP • Výchozím řešením může být libovolné základní přípustné řešení DP podle definice 2 • Výchozí řešení lze vypočítat přímo (není třeba pomocných proměnných) • Z řady aproximačních metod probereme tři typické reprezentanty: − metodu severozápadního rohu (SZR) − indexní metodu − Vogelovu aproximační metodu (VAM) © L&K 31

METODA SZR 1. Začneme políčkem (1, 1), tj položíme r=1, s =1, ar'= ar, bs'= bs 2. Tím určíme obsazované políčko (r, s) a základní proměnnou xrs 3. Určíme hodnotu proměnné xrs : xrs = min (ar’, bs’) = t (8. 10) 4. Opravíme kapacitu a požadavek: ar'= ar' - t (8. 11) bs'= bs' – t (kde apostrof ' označuje průběžně opravo vané hodnoty kapacit a požadavků) © L&K 32

5. Jestliže se vynuluje kapacita, tj. ar' = 0, vyškrtneme r−tý řádek a zvýšíme řádkový index o 1: r = r+1 6. Vynuluje–li se požadavek, tj. bs' = 0, vyškrtneme s−tý sloupec a zvýšíme sloupcový index o 1: s = s+1 7. Vracíme se k bodu 3. . . ? • Obsadíme tak m+n− 2 políček • Na poslední políčko (m, n) dosadíme xmn = ar' = bs' = t © L&K 33

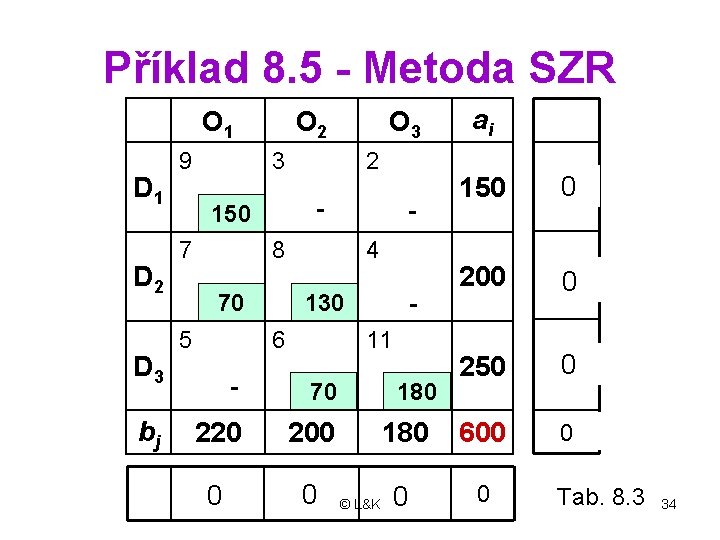
Příklad 8. 5 - Metoda SZR O 1 D 2 D 3 bj 9 O 2 3 2 - 150 7 8 70 5 O 3 4 130 6 11 ai 150 0 150 200 130 0 250 180 450 380 0 600 - 70 220 200 180 600 220 70 0 200 0 © L&K 180 70 0 250 180 0 450 380 600 180 Tab. 8. 3 34

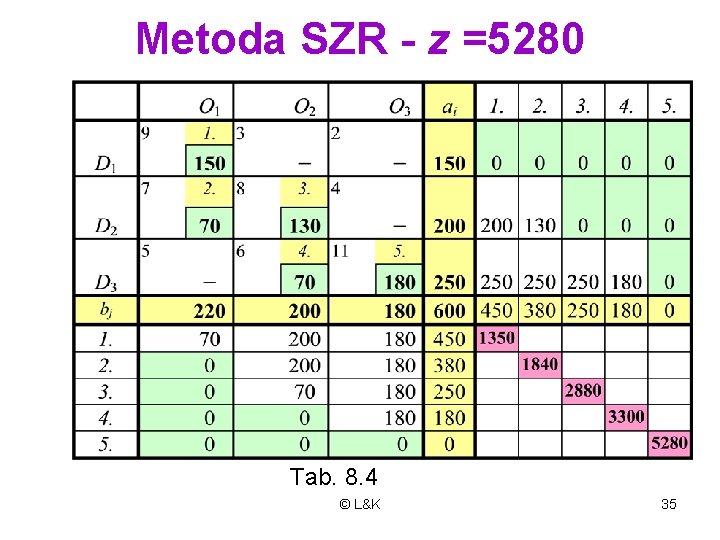
Metoda SZR - z =5280 Tab. 8. 4 © L&K 35

INDEXNÍ METODA 1. Obsazujeme vždy nevyškrtnuté políčko s nejnižší cenou 2. Určíme hodnotu proměnné podle (8. 10) 3. Opravíme kapacitu a požadavek podle (8. 11) 4. Vynuluje-li se kapacita, vyškrtneme řádek 5. Vynuluje-li se požadavek, vyškrtneme sloupec 6. Vracíme se k bodu 1. © L&K 36

Zpřesnění algoritmu • Jestliže jsme našli několik stejných nejmenších cenových koeficientů, dáme přednost políčku, na které můžeme dosadit větší hodnotu proměnné: • Je−li např. c 23=1 a x 23=min(100, 200)=100 a c 33=1 a x 33=min(300, 200)=200, obsadíme políčko (3, 3) • Poznámka: V posledním řádku (sloupci) obsadíme všechna volná políčka v libovolném pořadí © L&K 37

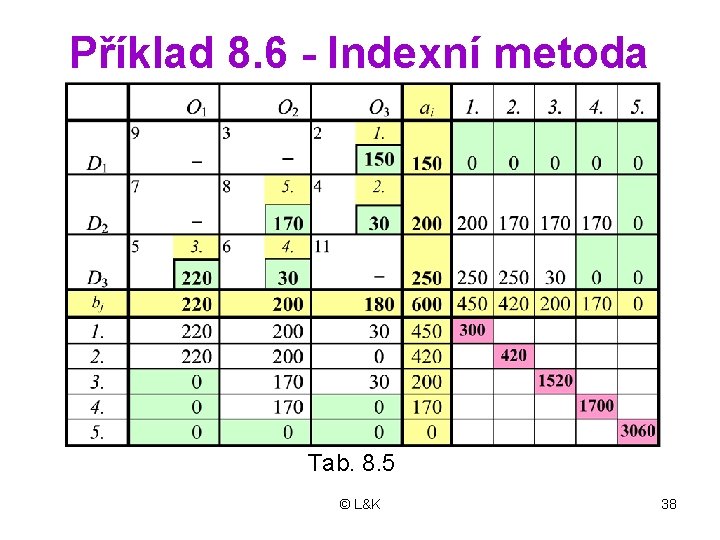
Příklad 8. 6 - Indexní metoda Tab. 8. 5 © L&K 38

VAM 1. Vypočteme rozdíl mezi druhou nejnižší a nejnižší cenou v každém řádku a sloupci 2. Najdeme nejvyšší rozdíl 3. Zde najdeme nejnižší cenu a určíme obsazené políčko 4. Podle (8. 10) vypočteme hodnotu základní proměnné 5. Opravíme pravé strany podle (8. 11) 6. Vracíme se k bodu 1 © L&K 39

Zpřesnění algoritmu 1. Jestliže vyškrtneme jen řádek, stačí přepočítat sloupcové rozdíly, vyškrtneme-li sloupec, přepočteme jen řádkové rozdíly 2. Na konci výpočtu zbude jeden řádek nebo sloupec → obsadíme všechna volná pole 3. Existuje více stejných nejvyšších rozdílů: − dáme přednost políčku s nejnižší cenou − ve druhém pořadí dáme přednost políč ku, na které můžeme dosadit větší hod notu (viz indexní metoda) © L&K 40

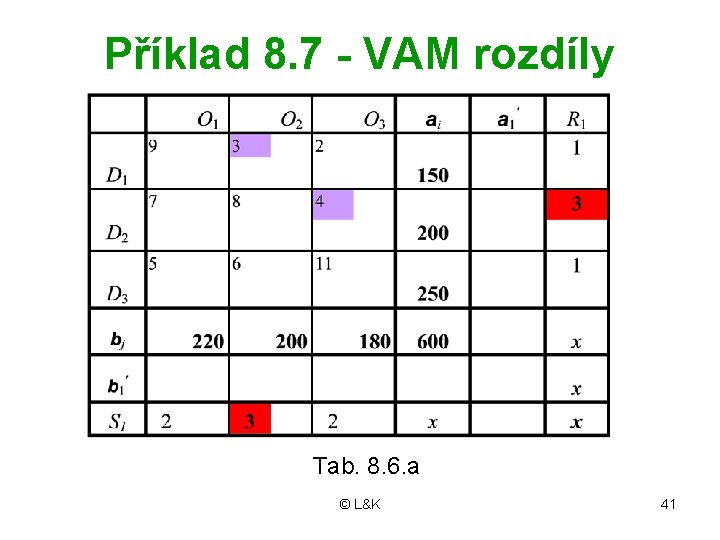
Příklad 8. 7 - VAM rozdíly Tab. 8. 6. a © L&K 41

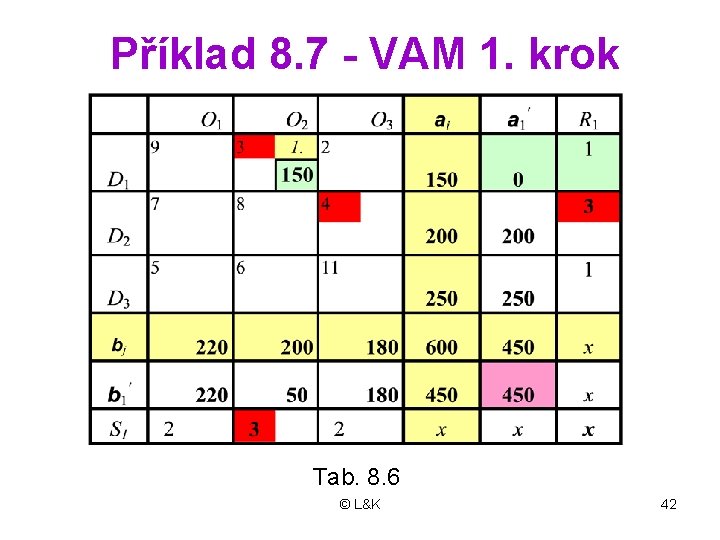
Příklad 8. 7 - VAM 1. krok Tab. 8. 6 © L&K 42

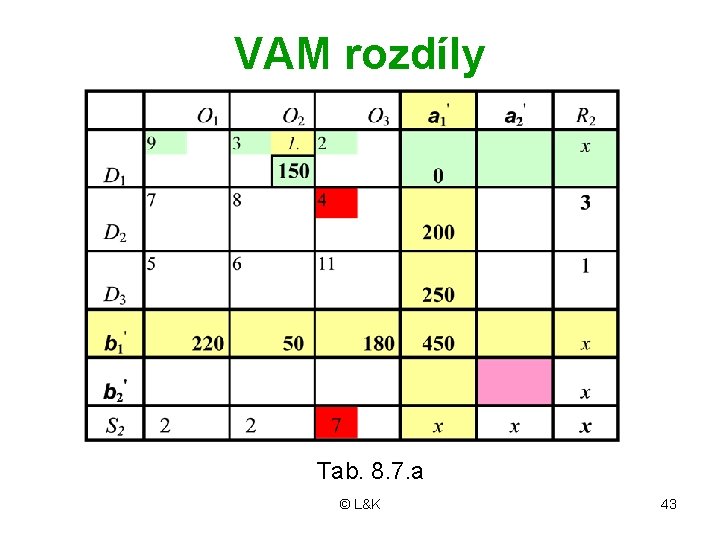
VAM rozdíly Tab. 8. 7. a © L&K 43

VAM 2. krok Tab. 8. 7 © L&K 44

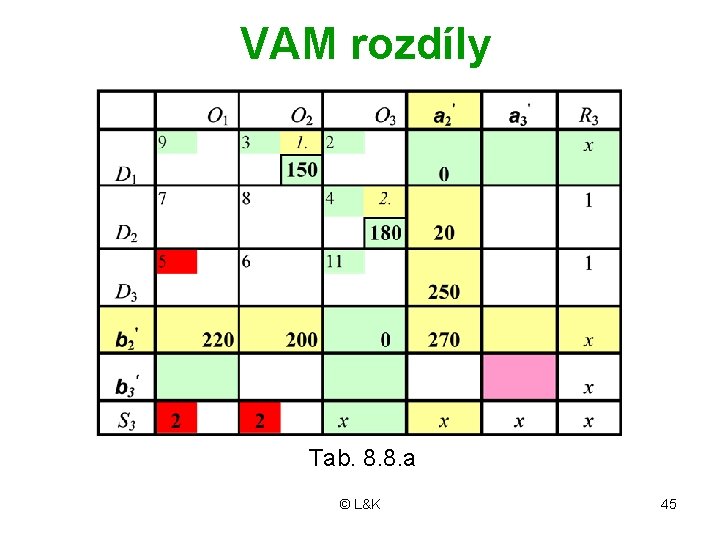
VAM rozdíly Tab. 8. 8. a © L&K 45

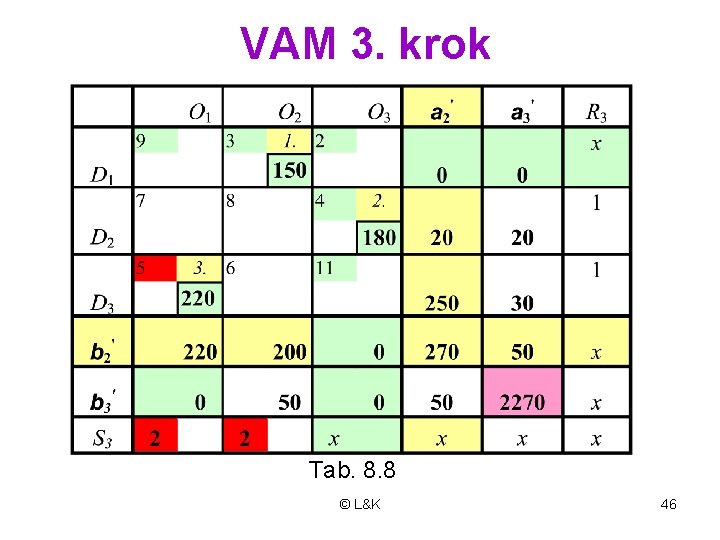
VAM 3. krok Tab. 8. 8 © L&K 46

VAM – 4. krok Tab. 8. 9 • V posledním zbylém sloupci obsazujeme volná políčka © L&K 47

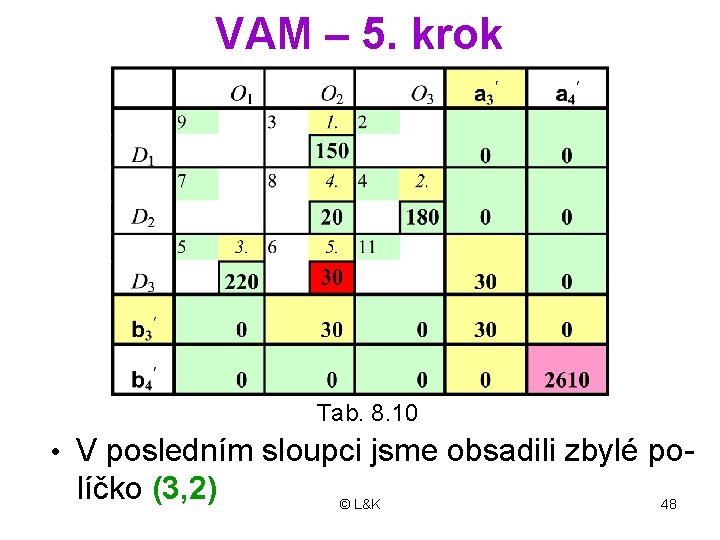
VAM – 5. krok Tab. 8. 10 • V posledním sloupci jsme obsadili zbylé po- líčko (3, 2) © L&K 48

NEVYROVNANÝ DP • Nevyrovnaný dopravní problém , kde (8. 12) upravíme na vyrovnaný: 1. Je-li > , přidáme fiktivního odběratele s požadavkem bn+1= © L&K (8. 13) 49

• • • Cenové koeficienty jsou rovny nule Dodávka fiktivnímu odběrateli znamená neprodané zboží Přidáním fiktivního odběratele rozšíříme dopravní tabulku o sloupec Počítáme-li výchozí řešení indexní metodou, obsazujeme ho jako poslední V metodě VAM počítáme s nulovými cenami ve fiktivním sloupci jako s ostatními, tj. považujeme je za nejnižší cenu © L&K 50

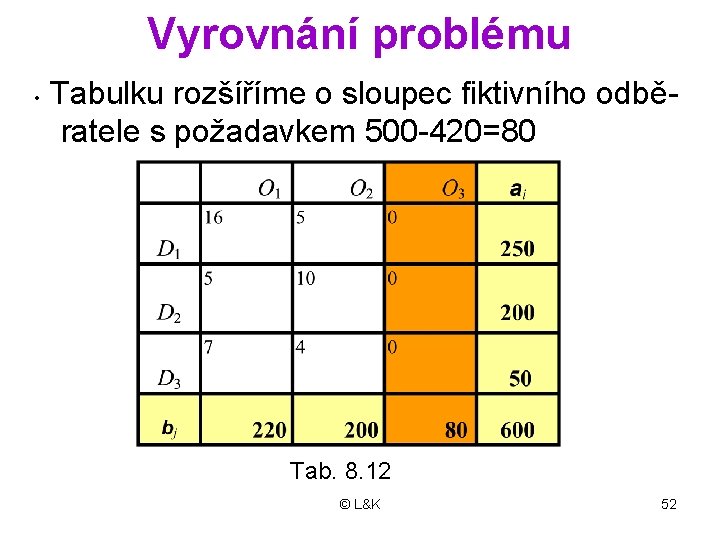
Příklad 8. 8 Tab. 8. 11 • V tabulce jsou zadány kapacity, požadav- ky a cenové koeficienty DP • Vypočtěte výchozí řešení indexní meto dou a metodou VAM (srovnejte hodnoty účelových funkcí. . . ) © L&K 51

Vyrovnání problému Tabulku rozšíříme o sloupec fiktivního odbě ratele s požadavkem 500 -420=80 • Tab. 8. 12 © L&K 52

Indexní metoda Tab. 8. 13 • Hodnota účelové funkce z = 2270 © L&K 53

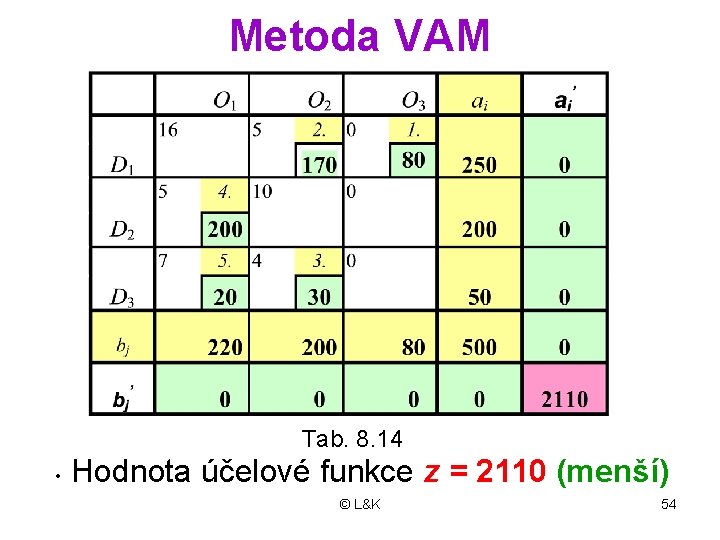
Metoda VAM Tab. 8. 14 • Hodnota účelové funkce z = 2110 (menší) © L&K 54

• < 2. Je-li , přidáme fiktivního dodavatele s kapacitou am+1= • • - (8. 14) Cenové koeficienty u fiktivního dodavatele jsou opět rovny nule Dodávka od fiktivního dodavatele znamená nesplněný požadavek © L&K 55

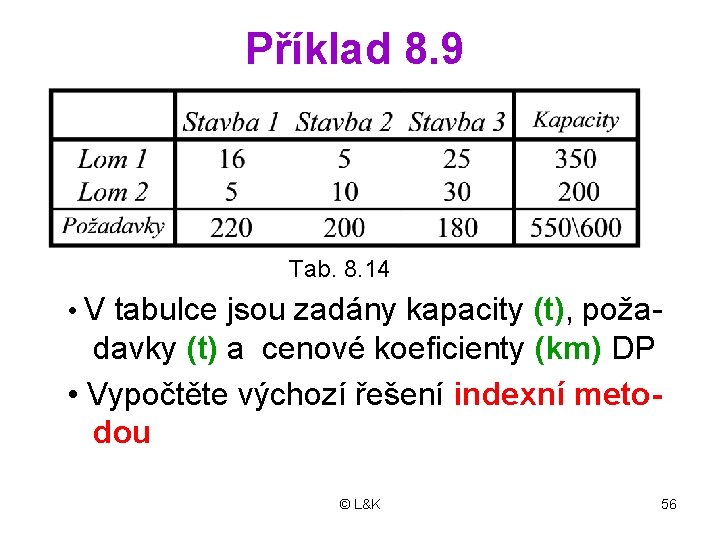
Příklad 8. 9 Tab. 8. 14 • V tabulce jsou zadány kapacity (t), poža- davky (t) a cenové koeficienty (km) DP • Vypočtěte výchozí řešení indexní meto dou © L&K 56

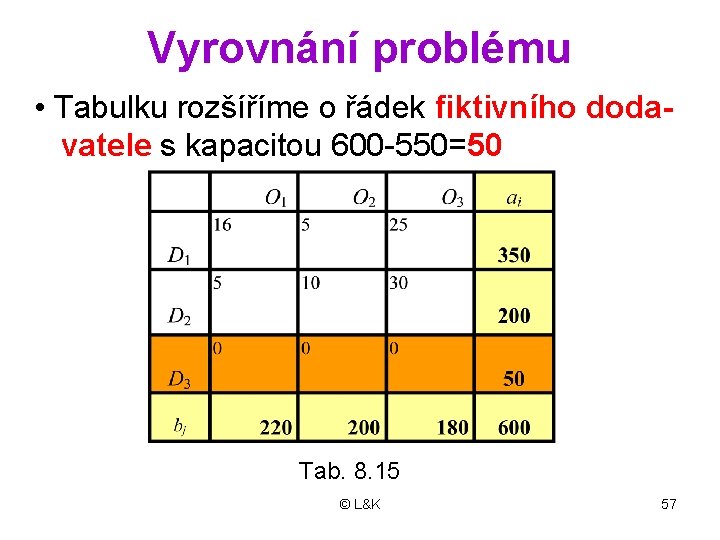
Vyrovnání problému • Tabulku rozšíříme o řádek fiktivního doda- vatele s kapacitou 600 -550=50 Tab. 8. 15 © L&K 57

Indexní metoda Tab. 8. 16 • Hodnota účelové funkce z = 5570 © L&K 58

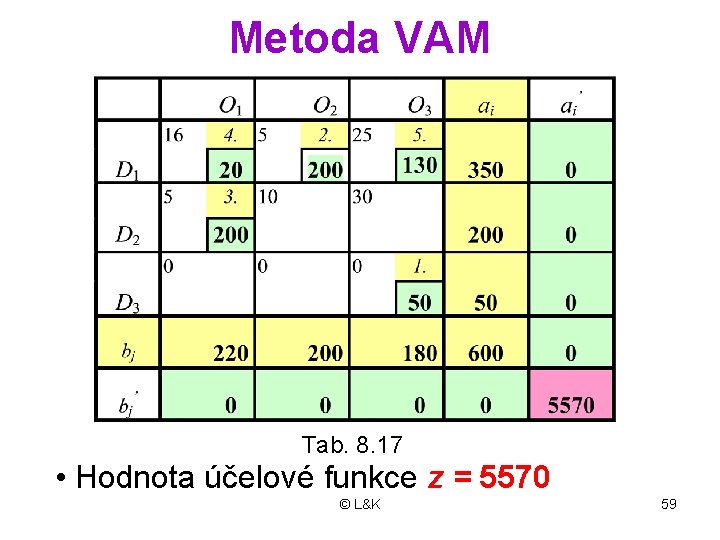
Metoda VAM Tab. 8. 17 • Hodnota účelové funkce z = 5570 © L&K 59

KONEC © L&K 60