4 EK 213 LINERN MODELY ter 11 00




































- Slides: 50

4 EK 213 – LINEÁRNÍ MODELY Úterý 11: 00 – 12: 30 hod. učebna 212 RB © Lagová, Kalčevová © L&K

2. PŘEDNÁŠKA MATEMATICKÝ MODEL ÚLOHY LP © L&K 2

OSNOVA PŘEDNÁŠKY • • • Obecná formulace MM Množina přípustných řešení úlohy LP Optimální řešení úlohy LP Rozbor řešitelnosti úlohy LP Standardní tvar MM úlohy LP Přídatné proměnné v modelu úlohy LP © L&K 3

OBECNÁ FORMULACE MM • Na soustavě vlastních omezení a 11 x 1 + a 12 x 2 +. . . + a 1 nxn R b 1 a 21 x 1 + a 22 x 2 +. . . + a 2 nxn R b 2. . . (2. 1) am 1 x 1+ am 2 x 2 +. . . + amnxn R bm a podmínek nezápornosti xj ≥ 0 , j = 1, 2, . . . , n (2. 2) nalézt extrém účelové funkce z = c 1 x 1 + c 2 x 2 +. . . + cnxn (2. 3) © L&K 4

• kde je xj. . . proměnná modelu (strukturní) aij. . . strukturní koeficient bi. . . pravá strana i-tého omezení cj. . . cenový koeficient j-té proměnné (cena) R. . . jedno z relačních znamének ≤, ≥, = n. . . počet strukturních proměnných modelu m. . . počet vlastních omezení modelu i = 1, 2, . . . , m, j = 1, 2, . . . , n © L&K 5

EKONOMICKÁ INTERPRETACE • xj. . . úroveň j-tého procesu (počet jednotek j−té činnosti) • bi. . . úroveň i-tého činitele (maximální nebo minimální možná hodnota) • aij. . . norma spotřeby, popř. produkce i-tého činitele na jednotku j-tého procesu • cj. . . cena j-tého procesu • i = 1, 2, . . . , m, j = 1, 2, . . . , n © L&K 6

Příklad 2. 1 • Formulujte MM úlohy z příkladu 1. 1 ve tvaru (2. 1) – (2. 3): na množině řešení omezení x 1 + 2 x 2 ≤ 120 x 1 + 4 x 2 ≤ 180 x 1 − x 2 ≥ 90 x 1 ≤ 110 xj ≥ 0, j = 1, 2 nalézt maximum účelové funkce z = 40 x 1 + 60 x 2 © L&K 7

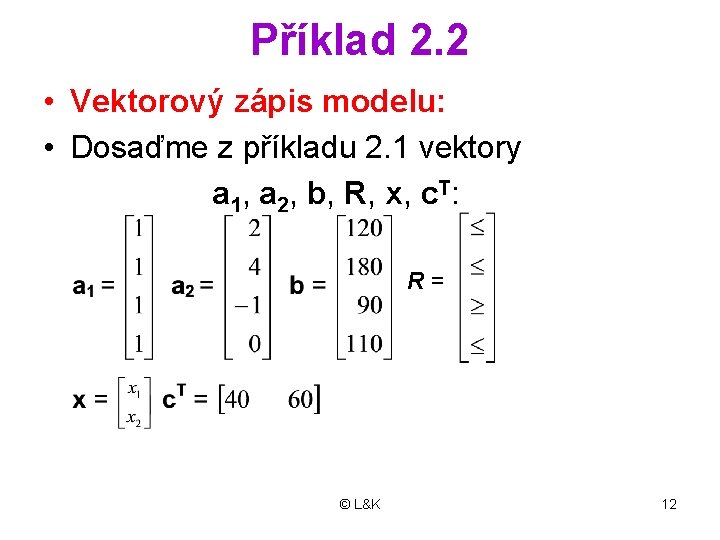
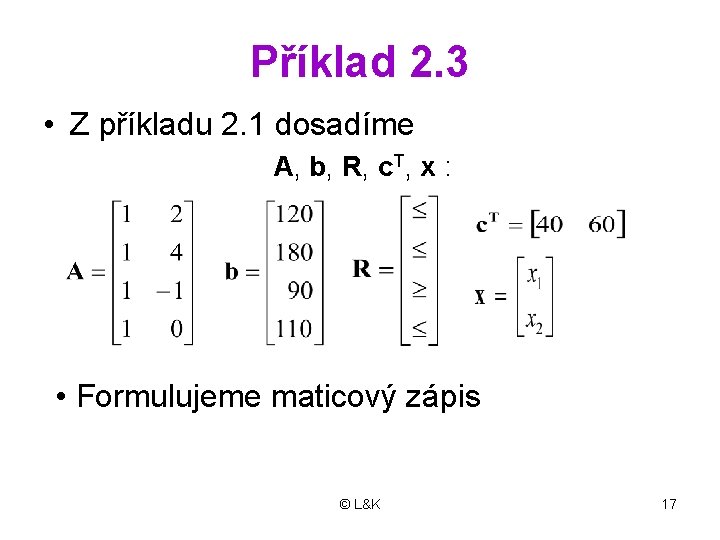
• kde jsou: x 1, x 2. . . strukturní proměnné, a 11=1, a 12=2, a 21=1, a 22=4, a 31=1, a 32=-1, a 41=1, a 42=0. . . strukturní koeficienty, b 1=120, b 2=180, b 3= 90, b 4=110. . . pravé strany omezení, c 1=40, c 2=60. . . cenové koeficienty © L&K 8

Další způsoby formulace MM • • Vektorový zápis Maticový zápis Zápis pomocí sumací Různé způsoby zápisu budeme ilustrovat na kapacitní úloze z příkladu 1. 1 © L&K 9

Vektorový zápis obecného MM Nalézt na soustavě vlastních omezení a 1 x 1 + a 2 x 2 +. . . + an xn R b (2. 4) a podmínek nezápornosti x≥ 0 (2. 5) extrém účelové funkce z = c. Tx. . . max (min. ) (2. 6) © L&K 10

kde je: x =(x 1, x 2, . . . , xn)T . . . vektor struktur- ních proměnných a 1=(a 11, a 21, . . . , am 1)T a 2=(a 12, a 22, . . . , am 2)T . . . vektor strukturních koeficientů an=(a 1 n, a 2 n, . . . , amn)T b =(b 1, b 2, . . . , bm)T . . . vektor pravých stran omezení. . . vektor cen c. T=(c 1, c 2, . . . , cn) R. . . vektor relačních znamének ≤, ≥, = © L&K 11

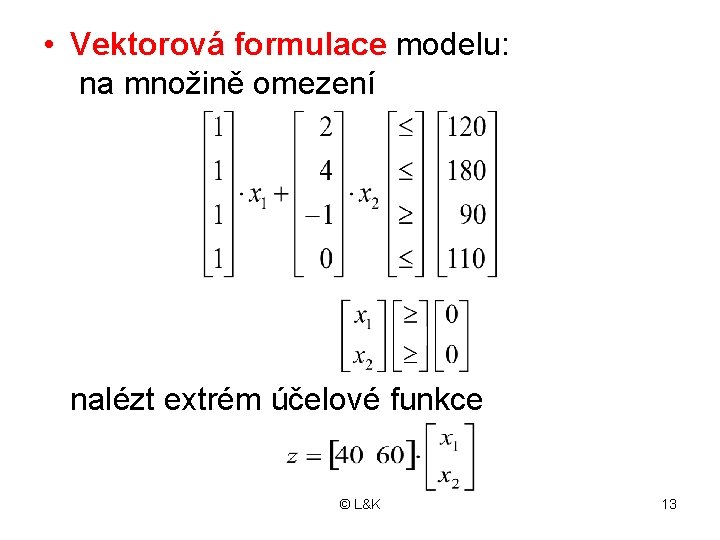
Příklad 2. 2 • Vektorový zápis modelu: • Dosaďme z příkladu 2. 1 vektory a 1, a 2, b, R, x, c. T: R= © L&K 12

• Vektorová formulace modelu: na množině omezení nalézt extrém účelové funkce © L&K 13

• Rozepište tento vektorový model: . . ? © L&K 14

Maticový zápis MM • Nejstručnější je maticový zápis MM: za podmínek Ax R b (2. 7) x≥ 0 maximalizovat (minimalizovat) účelovou funkci z = c. T x (2. 8) © L&K 15

kde je: x = (x 1, x 2, . . . , xn)T. . . vektor strukturních proměnných, A = [aij]mxn. . . matice strukturních koeficientů, b = (b 1, b 2, . . . , bm)T. . . vektor pravých stran omezení, c. T = (c 1, c 2, . . . , cn). . . vektor cenových koeficientů, R. . . je vektor relačních znamének ≤, ≥, = © L&K 16

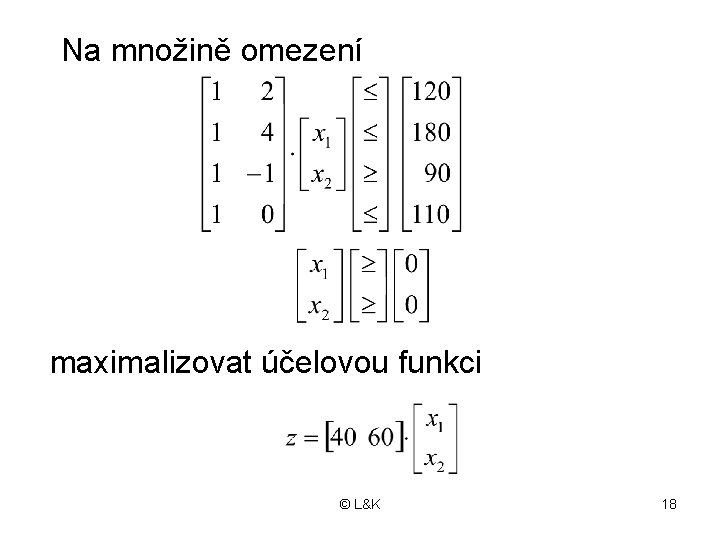
Příklad 2. 3 • Z příkladu 2. 1 dosadíme A, b, R, c. T, x : • Formulujeme maticový zápis © L&K 17

Na množině omezení maximalizovat účelovou funkci © L&K 18

• Rozepište tento maticový model: . . . ? © L&K 19

Zápis MM pomocí sumací Za podmínek i = 1, 2, . . . , m (2. 9) j = 1, 2, . . . , n maximalizovat účelovou funkci (2. 10) © L&K 20

POZOR ! • Při psaní vzorců je nutné dodržovat určitá elementární pravidla • Není možno kombinovat libovolně různé způsoby zápisu • Je nutno respektovat pravidla maticového počtu • Je třeba definovat všechny použité symboly • Je nutno určit definiční obor všech použitých indexů © L&K 21

CHYBY V ZÁPISU VZORCŮ Chybný zápis Správný zápis aijxj = bi, i=1, . . . , m Axj = b z = x. c. T z = c. T. x x. A = b A. x = b B. u. T = xj u TB = x ti = bi/ci, i=1, . . . , m t = b/c © L&K 22

Přípustné řešení úlohy LP • Nezáporné řešení soustavy vlastních omezení (2. 1) nazveme přípustné řešení (PŘ) • Úloha LP má: - nekonečně mnoho přípustných řešení - žádné přípustné řešení • Množina PŘ je: - konvexní s konečným počtem krajních bodů (definujte !) omezená nebo neomezená - prázdná množina © L&K 23

• Pokud je množina PŘ omezená, je to konvexní polyedr (definujte !) • Která ze zobrazených množin je konvexním polyedrem. . . . . ? © L&K 24

Optimální řešení úlohy LP • Mezi nekonečným množstvím přípustných řešení hledáme to, které je nejlepší, tj. maximalizuje (popř. minimalizuje) hodnotu účelové funkce • Takové řešení nazveme optimální (OŘ) • Úloha LP má: - jedno optimální řešení - nekonečně mnoho optimálních řešení - žádné optimální řešení © L&K 25

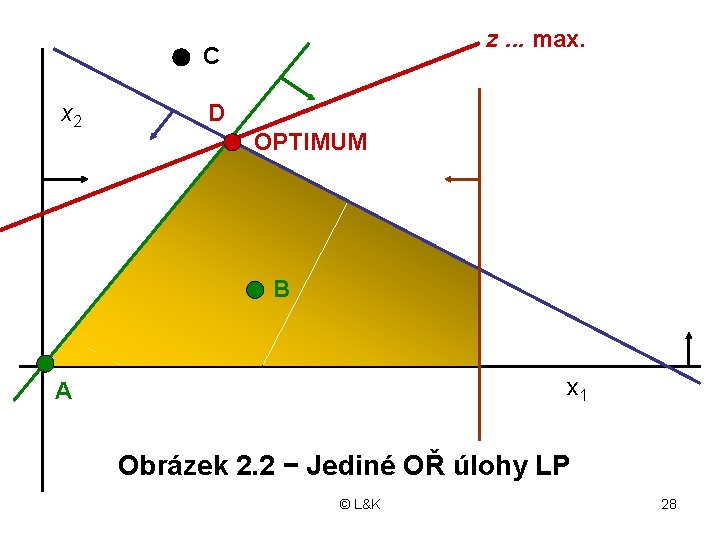
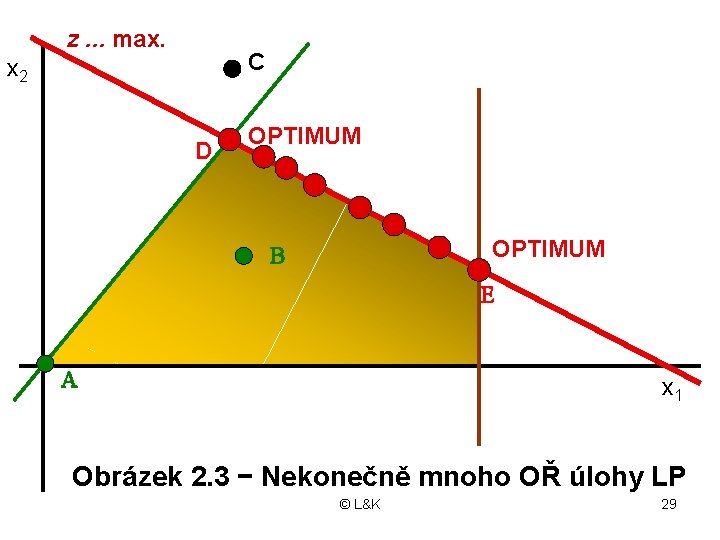
Rozbor řešitelnosti 1. Je-li množinou PŘ konvexní polyedr, má úloha LP vždy optimální řešení • Účelová funkce může na této množině nabývat jak svého maxima, tak minima • Optimální řešení může být: - jedno (obrázek 2. 2) - nekonečně mnoho (obrázek 2. 3) © L&K 26

• Jediné OŘ je ve vrcholu (krajním bodu) konvexní množiny PŘ • Má−li úloha LP nekonečně mnoho OŘ, je účelová funkce rovnoběžná s hranicí (hranou, stěnou, nadrovinou) konvexní množiny • Optimálním řešením je každý bod této hranice – konvexní obal krajních bodů • Ve dvourozměrném prostoru je to množina konvexních kombinací dvou krajních bodů této hranice (tj. úsečka mezi nimi) © L&K 27

z. . . max. C x 2 D OPTIMUM B x 1 A Obrázek 2. 2 − Jediné OŘ úlohy LP © L&K 28

z. . . max. C x 2 D OPTIMUM B E A x 1 Obrázek 2. 3 − Nekonečně mnoho OŘ úlohy LP © L&K 29

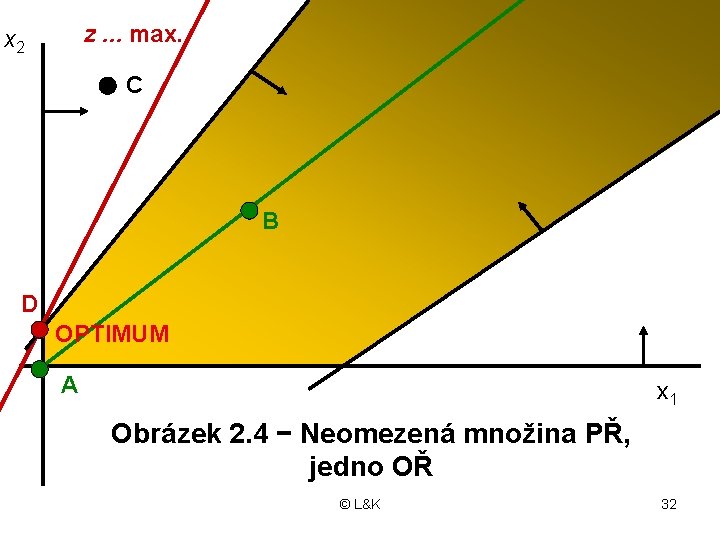
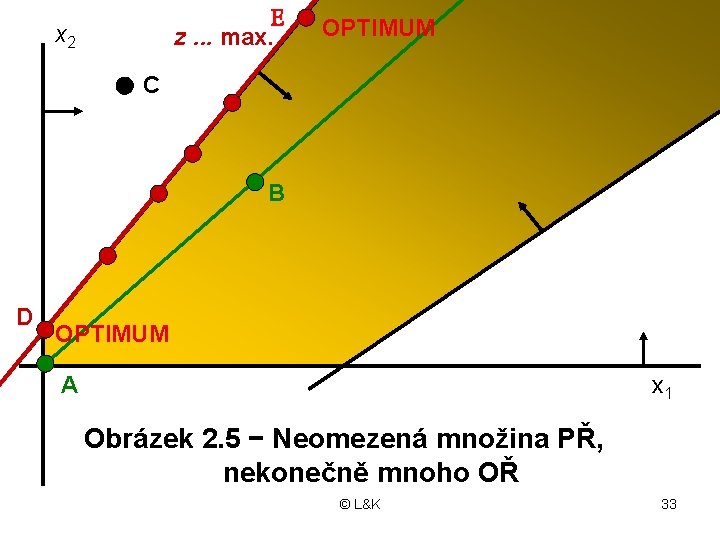
2. Neomezená množina PŘ • Obsahuje alespoň jednu polopřímku • Na této množině může mít úloha LP: - jedno OŘ - nekonečně mnoho OŘ - žádné OŘ 1. Jedno OŘ leží ve vrcholu množiny PŘ 2. Nekonečně mnoho OŘ tvoří ve dvourozměrném prostoru polopřímku (paprsek) © L&K 30

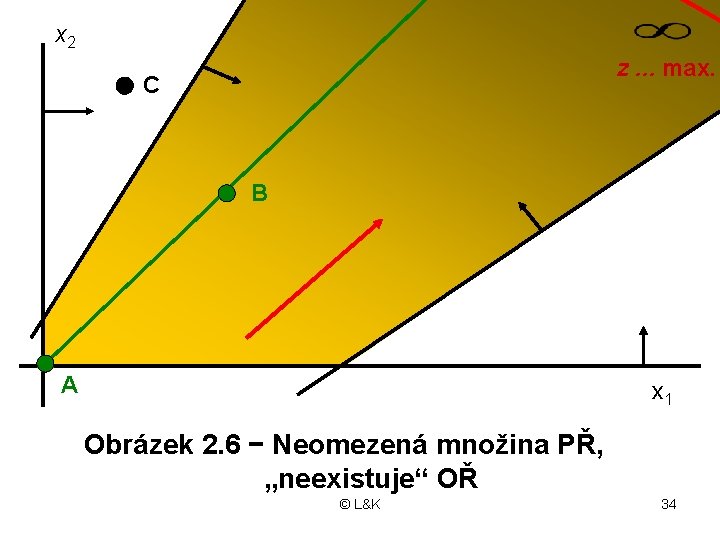
3. OŘ neexistuje: - konvexní množina PŘ je neomezená ve směru zadaného extrému účelové funkce (obrázek 2. 7) - účelová funkce může na této množině nabývat neomezených hodnot - v tomto případě existuje nekonečně mnoho přípustných řešení - nelze ale určit optimální hodnotu účelové funkce © L&K 31

z. . . max. x 2 C B D OPTIMUM A x 1 Obrázek 2. 4 − Neomezená množina PŘ, jedno OŘ © L&K 32

E z. . . max. x 2 OPTIMUM C B D OPTIMUM A x 1 Obrázek 2. 5 − Neomezená množina PŘ, nekonečně mnoho OŘ © L&K 33

x 2 z. . . max. C B A x 1 Obrázek 2. 6 − Neomezená množina PŘ, „neexistuje“ OŘ © L&K 34

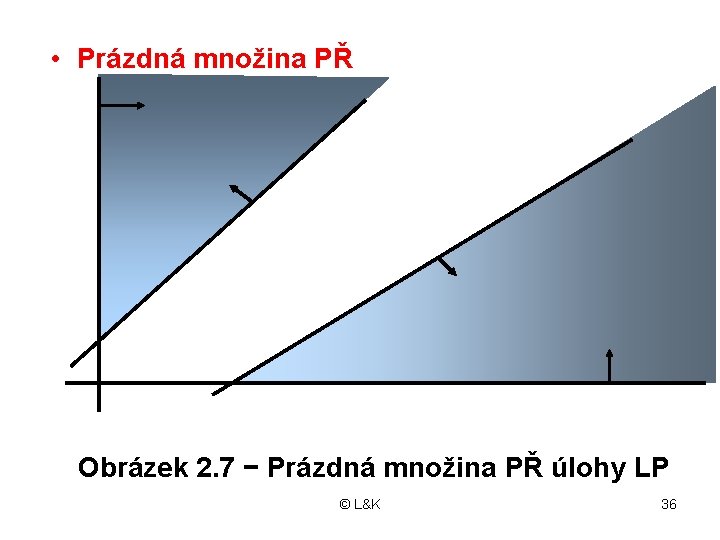
3. Prázdná množina PŘ • Soustava vlastních omezení MM je nekonzistentní • Neexistuje přípustné řešení úlohy LP • Množina PŘ je prázdná • Tudíž neexistuje optimální řešení této úlohy © L&K 35

• Prázdná množina PŘ Obrázek 2. 7 − Prázdná množina PŘ úlohy LP © L&K 36

ŘEŠENÍ MM • Pro zjednodušení výkladu přijmeme na začátku kurzu tyto dva předpoklady: 1. Všechna omezení modelu jsou zadána jako nerovnice: - rovnici převedeme na dvě nerovnice opačného typu, např. : 3 x 1 + 2 x 2 = 60 vyjádříme jako 3 x 1 + 2 x 2 ≤ 60 3 x 1 + 2 x 2 ≥ 60 © L&K 37

2. Budeme uvažovat MM s maximalizační účelovou funkcí • Minimalizační funkci f(x) upravíme na maximalizační z(x) podle z(x) = − f(x). . . max. kde min (f) = − max (z) • Např. funkci f = 20 x 1 + 10 x 2. . . min. převedeme na tvar z = − 20 x 1 − 10 x 2. . . max. © L&K 38

ÚPRAVA MM K VÝPOČTU • Metody řešení úloh LP pracují se soustavou rovnic, nikoliv se soustavou nerovnic Proč ? • Je proto třeba vlastní omezení zadaná ve tvaru nerovnic převést na rovnice Jak ? • Model rozšíříme o další proměnné, které nazveme přídatné proměnné © L&K 39

1. Nerovnice typu ≤: ai 1 x 1+ ai 2 x 2 +. . . + ainxn ≤ bi • K levé straně nerovnice přičteme přídatnou proměnnou: ai 1 x 1+ ai 2 x 2 +. . . + ainxn + xn+i = bi • Odtud je xn+i = bi – (ai 1 x 1+ ai 2 x 2 +. . . + ainxn) • Např. první omezení v příkladu (2. 1) x 1 + 2 x 2 ≤ 120 upravíme na: x 1 + 2 x 2 + x 3 = 120 © L&K 40

2. Nerovnice typu ≥: • Od levé strany nerovnice typu ≥ odečteme přídatnou proměnnou: ai 1 x 1+ ai 2 x 2 +. . . + ainxn − xn+i = bi • Odtud je xn+i = ai 1 x 1+ ai 2 x 2 +. . . + ainxn − bi • Např. třetí omezení v příkladu 2. 1 x 1 − x 2 ≥ 90 upravíme na: x 1 − x 2 − x 5 = 90 © L&K 41

• Přídatné proměnné jsou nezáporné • Mají svoji ekonomickou interpretaci, která je odvozena od ekonomické interpretace omezení • Přídatná proměnná v omezení typu ukazuje objem nevyužité kapacity • Přídatná proměnná v omezení typu ≥ ukazuje velikost překročení požadavku • Cena přídatné proměnné je vzhledem k její ekonomické interpretaci rovna nule © L&K 42

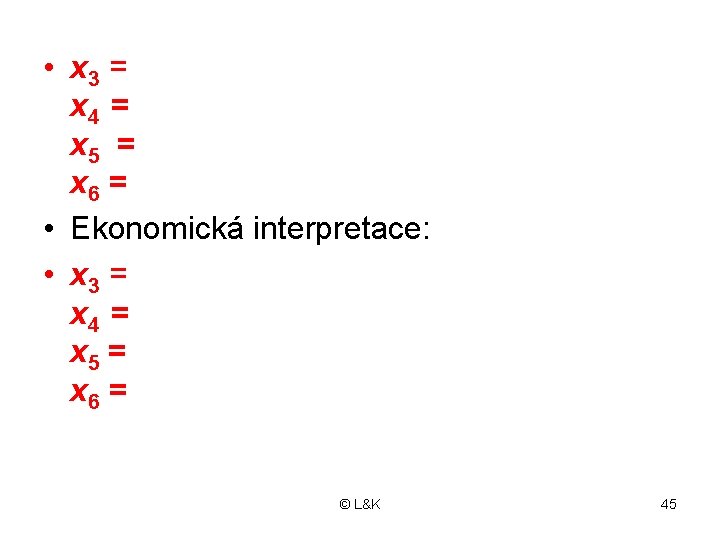
Příklad 2. 4 • Uvažujme soustavu vlastních omezení kapacitní úlohy z příkladu 2. 1: x 1 + 2 x 2 x 1 + 4 x 2 x 1 − x 2 x 1 © L&K ≤ 120 ≤ 180 ≥ 90 ≤ 110 43

• Nerovnice vyrovnáme na rovnice pomocí přídatných proměnných: x 1 + 2 x 2 + x 3 = 120 x 1 + 4 x 2 + x 4 = 180 x 1 − x 2 − x 5 = 90 x 1 + x 6 = 110 • Dosadíme x 1 = 110, x 2 = 5 (viz př. 1. 1) • Hodnoty přídatných proměnných. . . . ? • Ekonomická interpretace. . . . . ? © L&K 44

• x 3 = x 4 = x 5 = x 6 = • Ekonomická interpretace: • x 3 = x 4 = x 5 = x 6 = © L&K 45

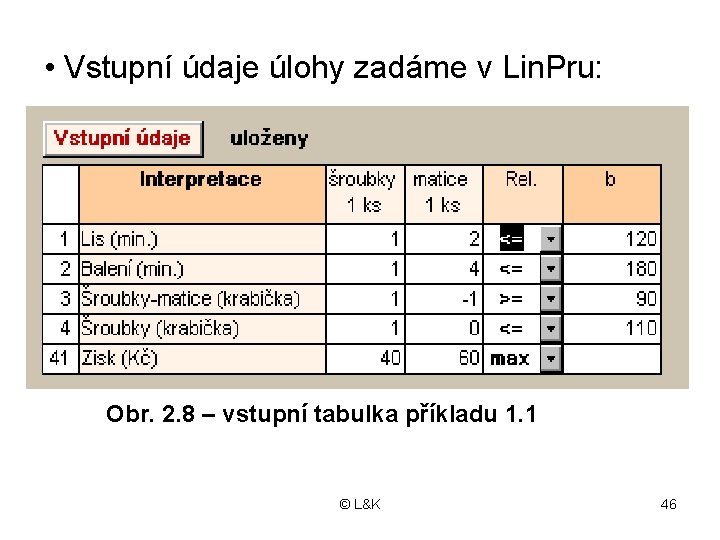
• Vstupní údaje úlohy zadáme v Lin. Pru: Obr. 2. 8 – vstupní tabulka příkladu 1. 1 © L&K 46

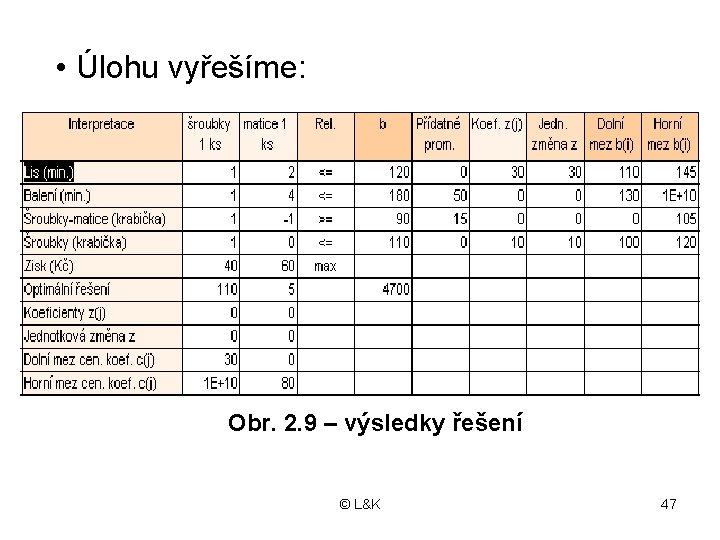
• Úlohu vyřešíme: Obr. 2. 9 – výsledky řešení © L&K 47

• Hodnoty strukturních proměnných : x 1 = 110, x 2 = 5, • Hodnoty přídatných proměnných: • x 3 = 0, x 4 = 50, x 5 = 15, x 6 = 0 • Stručněji: x = (110, 5, 0, 15, 0)T • Hodnota účelové funkce: z = 4700 © L&K 48

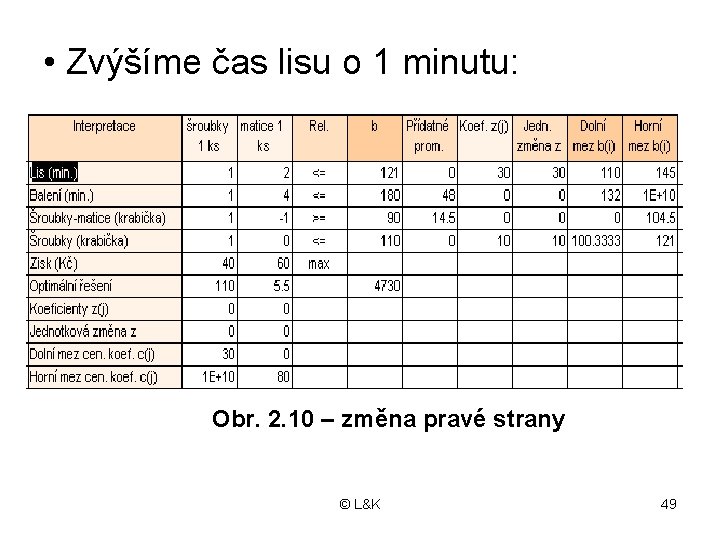
• Zvýšíme čas lisu o 1 minutu: Obr. 2. 10 – změna pravé strany © L&K 49

KONEC © L&K 50
 Linern
Linern Linern
Linern Quem acha um amigo encontra um tesouro
Quem acha um amigo encontra um tesouro Argentiho model
Argentiho model Modely oligopolu
Modely oligopolu Riadenie ľudských zdrojov
Riadenie ľudských zdrojov Plodolist
Plodolist Modely oligopolu
Modely oligopolu Poq model
Poq model Arima modely
Arima modely Socialni politika
Socialni politika Ceng 213
Ceng 213 Ceng 213
Ceng 213 Carnegie mellon
Carnegie mellon Schedule a hiring authority 5 cfr 213,3102(u)
Schedule a hiring authority 5 cfr 213,3102(u) Ct 213
Ct 213 Mis 213
Mis 213 132 213
132 213 Ek 213
Ek 213 Outline 213
Outline 213 15-213 introduction to computer systems
15-213 introduction to computer systems 5 state process model
5 state process model Cmu 213
Cmu 213 18-213 cmu
18-213 cmu Ct-213
Ct-213 Dr stephen daniels
Dr stephen daniels 15 213
15 213 Sbi 213
Sbi 213 15-213 cmu
15-213 cmu 15-213 cmu
15-213 cmu Rio_readinitb
Rio_readinitb Ct 213
Ct 213 213 table
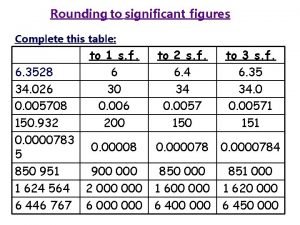
213 table What is 2 significant figures
What is 2 significant figures Cmu 15-213
Cmu 15-213 Ee 213
Ee 213 15 213
15 213 Cs 213 northwestern
Cs 213 northwestern 15-213 cmu
15-213 cmu Sigchild
Sigchild Ct 213
Ct 213 Outline 213
Outline 213 Poli 213
Poli 213 Zva-213-s+
Zva-213-s+ 18-213 cmu
18-213 cmu 15-213 introduction to computer systems
15-213 introduction to computer systems Ct 213
Ct 213 Q tér
Q tér Felix ter chian tan
Felix ter chian tan Participio presente
Participio presente No desenho abaixo a figura
No desenho abaixo a figura