Kapitola 4 ARIMA modely SAS Institute Bratislava 4

Kapitola 4 ARIMA modely SAS Institute, Bratislava

4. ARIMA modely 4. 1. Úvod 4. 2. Predbežná analýza 4. 3. Výber vhodných modelov 4. 4. Porovanie kvality modelov 4. 5. Výpočet prognózy SAS Institute, Bratislava 2

4. 1. Úvod p ARIMA modely o o o Auto. Regressive Integrated Moving-Average models sú konštruované iným spôsobom ako klasické modely princíp o hodnota časového radu je lineárna kombinácia o jej vlastných historických hodnôt o historických hodnôt reziduálnych odchýlok tzv. náhodných šokov Predkovia Počasie SAS Institute, Bratislava 3

4. 1. Úvod p ARIMA modely o o o vyžadujú náročnejšiu analýzu ako iné typy modelov pre väčšinu ekonomických veličín poskytujú lepšie výsledky proces analýzy má viacero fáz o o identifikácia modelu odhad modelu verifikácia modelu prognózovanie SAS Institute, Bratislava 4

4. 2. Predbežná analýza ČR p Predpoklad ARIMA modelov o o o ARIMA modely popisujú správanie časových radov s použitím minimálneho počtu parametrov takéto úsporné opatrenie, ale niečo stojí cenou za možnosti, ktoré poskytujú ARIMA modely je splnenie konkrétneho predpokladu stacionarity o štatistické vlastnosti časového radu sa v čase nemenia o hovoríme potom, že časový rad je stacionárny SAS Institute, Bratislava 5

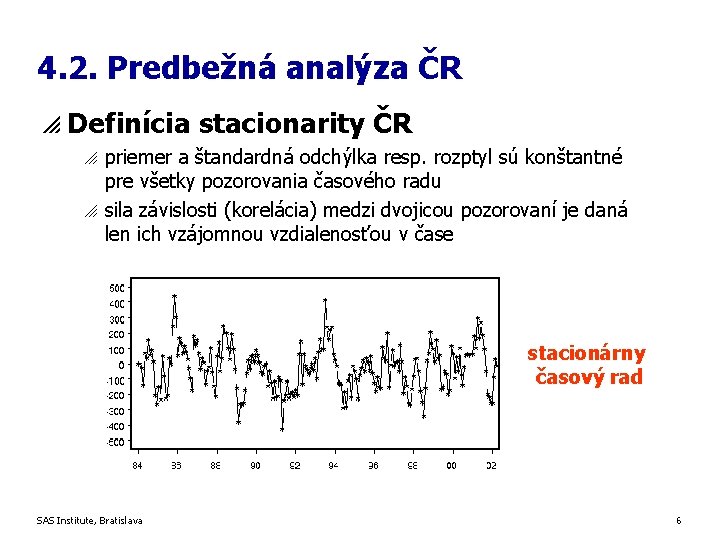
4. 2. Predbežná analýza ČR p Definícia stacionarity ČR o o priemer a štandardná odchýlka resp. rozptyl sú konštantné pre všetky pozorovania časového radu sila závislosti (korelácia) medzi dvojicou pozorovaní je daná len ich vzájomnou vzdialenosťou v čase stacionárny časový rad SAS Institute, Bratislava 6

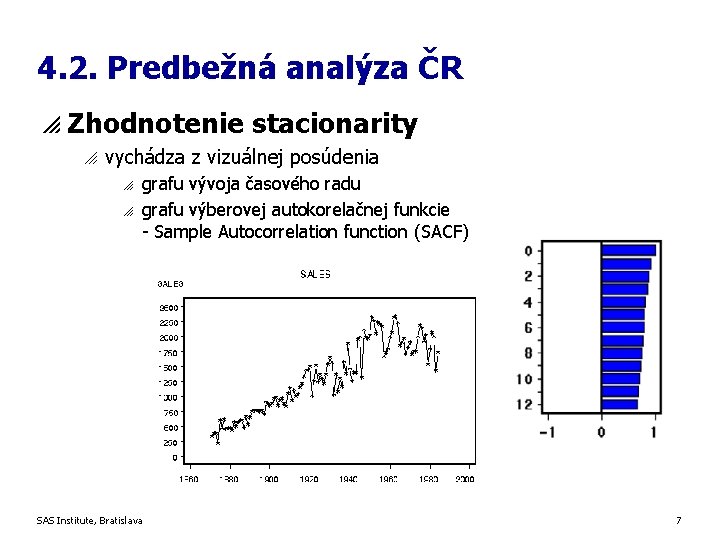
4. 2. Predbežná analýza ČR p Zhodnotenie stacionarity o vychádza z vizuálnej posúdenia o o grafu vývoja časového radu grafu výberovej autokorelačnej funkcie - Sample Autocorrelation function (SACF) SAS Institute, Bratislava 7

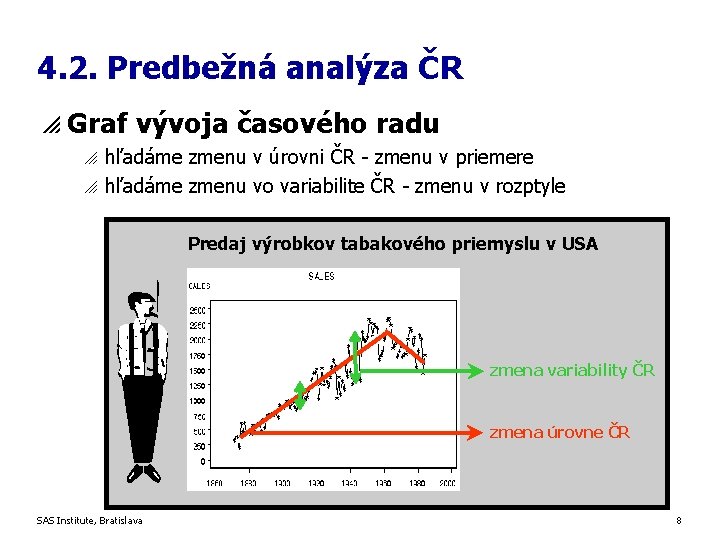
4. 2. Predbežná analýza ČR p Graf vývoja časového radu o o hľadáme zmenu v úrovni ČR - zmenu v priemere hľadáme zmenu vo variabilite ČR - zmenu v rozptyle Predaj výrobkov tabakového priemyslu v USA zmena variability ČR zmena úrovne ČR SAS Institute, Bratislava 8

4. 2. Predbežná analýza ČR p Graf výberovej autokorelačnej funkcie o autokorelácia ČR o o vzájomný lineárny vzťah - závislosť medzi pozorovaniami časového radu koeficient autokorelácie o meria silu autokorelácie medzi pozorovaniami časového radu, ktoré sú v čase od seba vzdialené o k okamihov k=0, 1, 2 …. o k je tzv. lag - oneskorenie určuje poradie koeficienta autokorelácie o o hodnoty z intervalu (-1 , 1) o o blízko 1 -1 +/0 silná pozitívna autokorelácia silná negatívna autokorelácia slabá lineárna autokorelácia neexistuje graf autokorelačnej funkcie o o o zobrazuje hodnoty koeficientov autokorelácie os x - poradie koeficienta autokorelácie os y - hodnota koeficienta autokorelácie SAS Institute, Bratislava 9

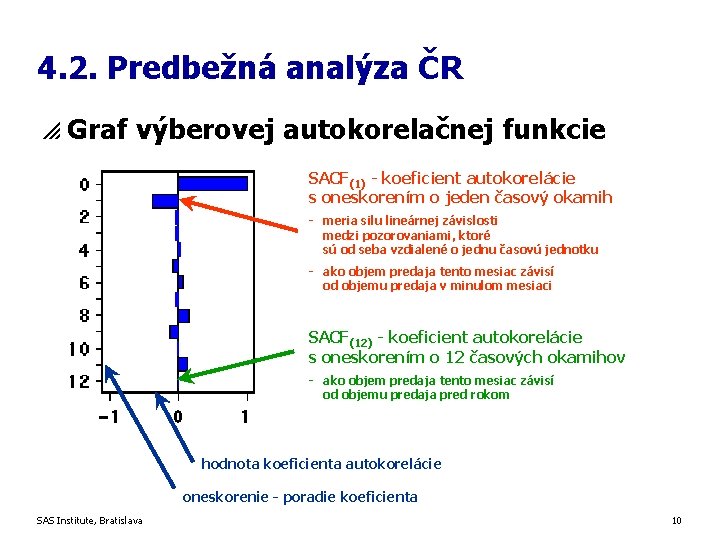
4. 2. Predbežná analýza ČR p Graf výberovej autokorelačnej funkcie SACF(1) - koeficient autokorelácie s oneskorením o jeden časový okamih - meria silu lineárnej závislosti medzi pozorovaniami, ktoré sú od seba vzdialené o jednu časovú jednotku - ako objem predaja tento mesiac závisí od objemu predaja v minulom mesiaci SACF(12) - koeficient autokorelácie s oneskorením o 12 časových okamihov - ako objem predaja tento mesiac závisí od objemu predaja pred rokom hodnota koeficienta autokorelácie oneskorenie - poradie koeficienta SAS Institute, Bratislava 10

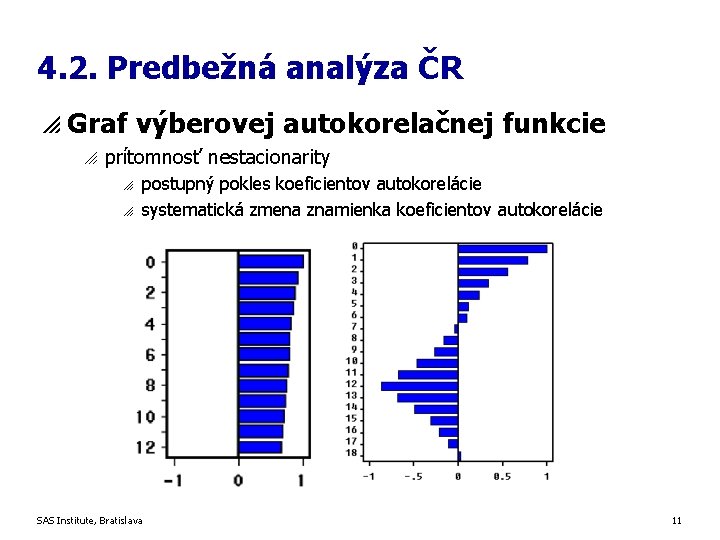
4. 2. Predbežná analýza ČR p Graf výberovej autokorelačnej funkcie o prítomnosť nestacionarity o o postupný pokles koeficientov autokorelácie systematická zmena znamienka koeficientov autokorelácie SAS Institute, Bratislava 11

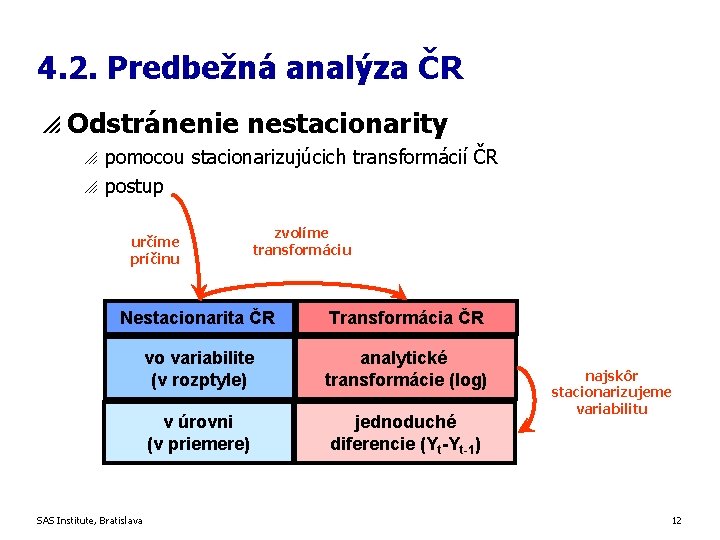
4. 2. Predbežná analýza ČR p Odstránenie nestacionarity o o pomocou stacionarizujúcich transformácií ČR postup určíme príčinu zvolíme transformáciu Nestacionarita ČR Transformácia ČR vo variabilite (v rozptyle) analytické transformácie (log) v úrovni (v priemere) jednoduché diferencie (Yt-Yt-1) SAS Institute, Bratislava najskôr stacionarizujeme variabilitu 12

4. 2. Predbežná analýza ČR p Stacionarizujúce transformácie o jednoduché diferencie o vypočítame nový časový rad o ako rozdiel hodnôt pôvodného časového radu o o môžu byť rôzneho rádu d= 1, 2, … jednoduché diferencie 1. rádu o Zt = Yt - Yt-1 o Zt = (1 - B ) Yt o B je operátor spätného chodu (backshift operátor) o definuje sa ako BYt = Yt-1 o jednoduché diferencie 2. rádu o o o SAS Institute, Bratislava Wt = Zt - Zt-1 Wt = (Yt - Yt-1) - (Yt-1 - Yt-2) Wt = Yt - 2 Yt-1 + Yt-2 Wt = Yt - 2 B Yt + B 2 Yt Wt = (1 - B )2 Yt dôležitý zápis v teórii ARIMA modelov 13

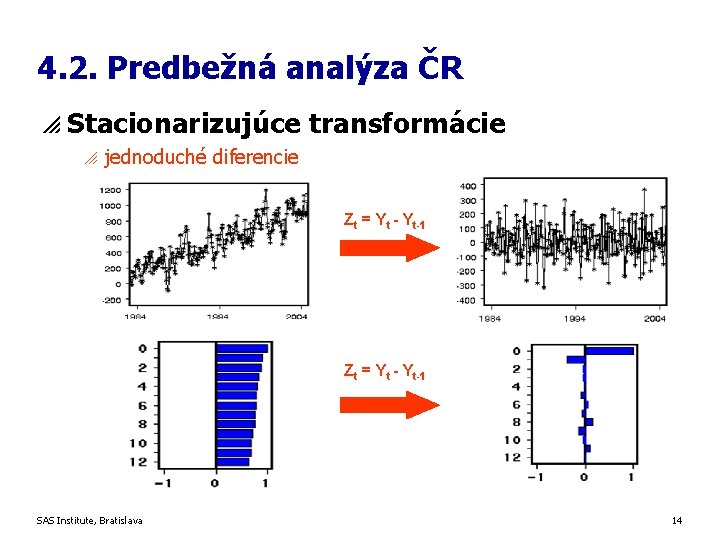
4. 2. Predbežná analýza ČR p Stacionarizujúce transformácie o jednoduché diferencie Zt = Yt - Yt-1 SAS Institute, Bratislava 14

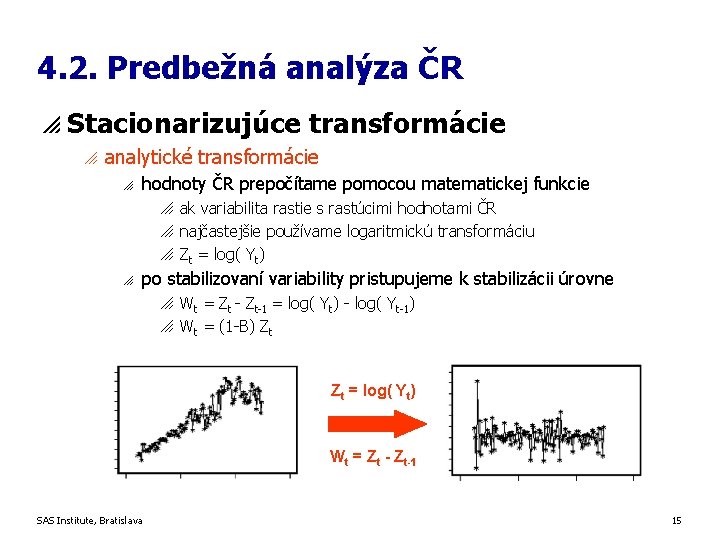
4. 2. Predbežná analýza ČR p Stacionarizujúce transformácie o analytické transformácie o hodnoty ČR prepočítame pomocou matematickej funkcie o ak variabilita rastie s rastúcimi hodnotami ČR o najčastejšie používame logaritmickú transformáciu o Zt = log( Yt) o po stabilizovaní variability pristupujeme k stabilizácii úrovne o Wt = Zt - Zt-1 = log( Yt) - log( Yt-1) o Wt = (1 -B) Zt Zt = log( Yt) Wt = Zt - Zt-1 SAS Institute, Bratislava 15

4. 2. Predbežná analýza ČR p Sezónnosť o všeobecne o o hodnota ČR závisí od konkrétnej sezóny - mesiaca, štvrťroka, v ktorom bola zaznamenaná ARIMA modely o hodnota ČR závisí od hodnoty v predchádzajúcich sezónach o od hodnoty ČR pred rokom a pod. o koeficienty autokorelácie pre k=dĺžka sezónny sú významne vysoké o sezónny ČR rad musí byť stacionárny aj zo sezónneho hľadiska o sezónna úroveň sa nemení o ak je stacionárna celková úroveň, sezónna úroveň nemusí byť stacionárna o sezónna variabilita sa nemení o ak je stacionárna celková variabilita, je stacionárna aj sezónna variabilita SAS Institute, Bratislava 16

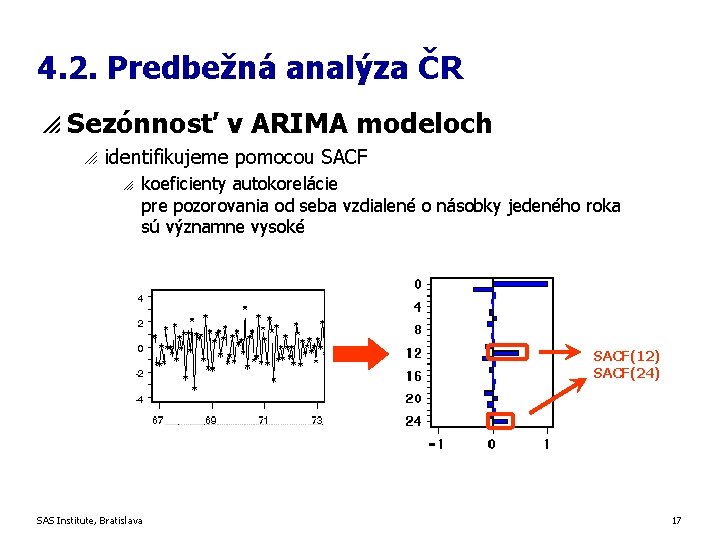
4. 2. Predbežná analýza ČR p Sezónnosť v ARIMA modeloch o identifikujeme pomocou SACF o koeficienty autokorelácie pre pozorovania od seba vzdialené o násobky jedeného roka sú významne vysoké SACF(12) SACF(24) SAS Institute, Bratislava 17

4. 2. Predbežná analýza ČR p Sezónnosť a stacionarita o o ak je ČR stacionárny v celkovej variabilite, je stacionárny aj v sezónnej variabilite o stacionarite v úrovni to neplatí o prítomnosť nestacionarity v sezónnej úrovni o sa prejaví v SACF o koeficienty autokorelácie so sezónnym oneskorením postupne klesajú Sezónna nestacionarita v úrovni ČR SAS Institute, Bratislava 18

4. 2. Predbežná analýza ČR p Odstránenie sezónnej nestacionarity o o použijeme sezónne stacionarizujúce transformácie koriguje sezónnu nestacionaritu úrovne ČR o o pri úprave jednoduchej nestacionarite v úrovni ČR sme použili jednoduché diferencie pri sezónnej nestacionarite úrovne použijeme sezónne diferencie SAS Institute, Bratislava 19

4. 2. Predbežná analýza ČR p Sezónne stacionarizujúce transformácie o sezónne diferencie o vypočítame nový časový rad o ako rozdiel hodnôt pôvodného časového radu, ktoré sú od seba vzdialené o jednu periódu (rok) o jednoduché diferencie 1. rádu sú väčšinou postačujúce o Zt = Yt - Yt-P o Zt = (1 - BP ) Yt o P je dĺžka periódy o B je operátor spätného chodu (backshift operátor) o definuje sa ako BYt = Yt-P Zt = Yt - Yt-P SAS Institute, Bratislava 20

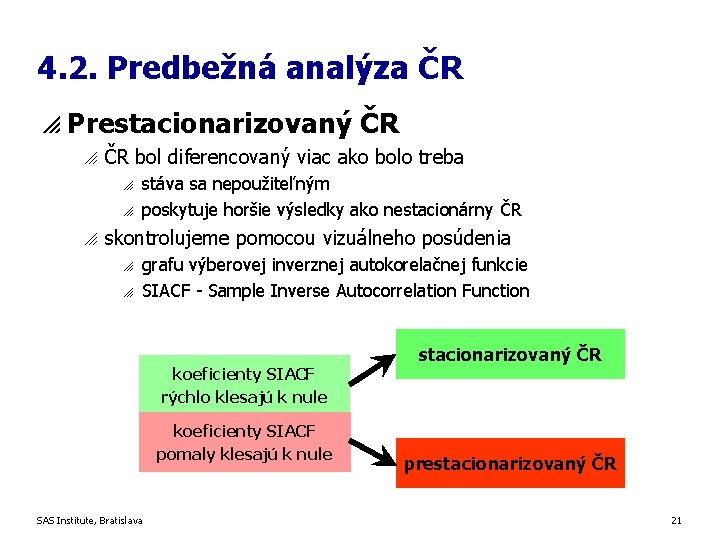
4. 2. Predbežná analýza ČR p Prestacionarizovaný ČR o ČR bol diferencovaný viac ako bolo treba o o o stáva sa nepoužiteľným poskytuje horšie výsledky ako nestacionárny ČR skontrolujeme pomocou vizuálneho posúdenia o o grafu výberovej inverznej autokorelačnej funkcie SIACF - Sample Inverse Autocorrelation Function koeficienty SIACF rýchlo klesajú k nule koeficienty SIACF pomaly klesajú k nule SAS Institute, Bratislava stacionarizovaný ČR prestacionarizovaný ČR 21

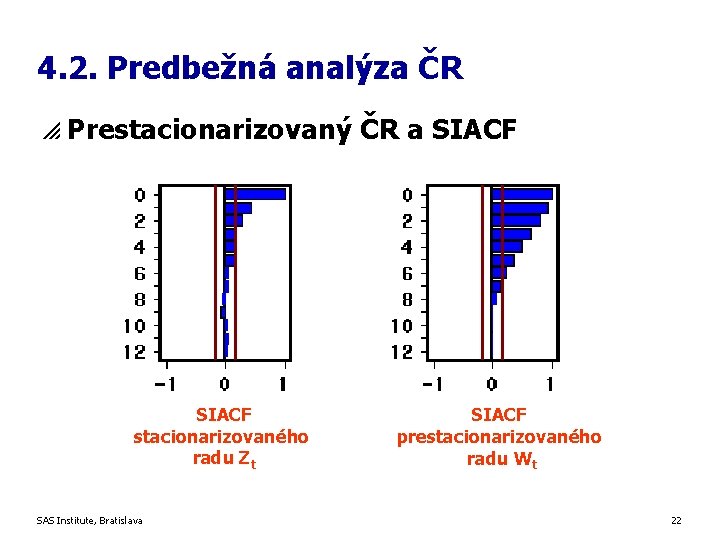
4. 2. Predbežná analýza ČR p Prestacionarizovaný ČR a SIACF stacionarizovaného radu Zt SAS Institute, Bratislava SIACF prestacionarizovaného radu Wt 22

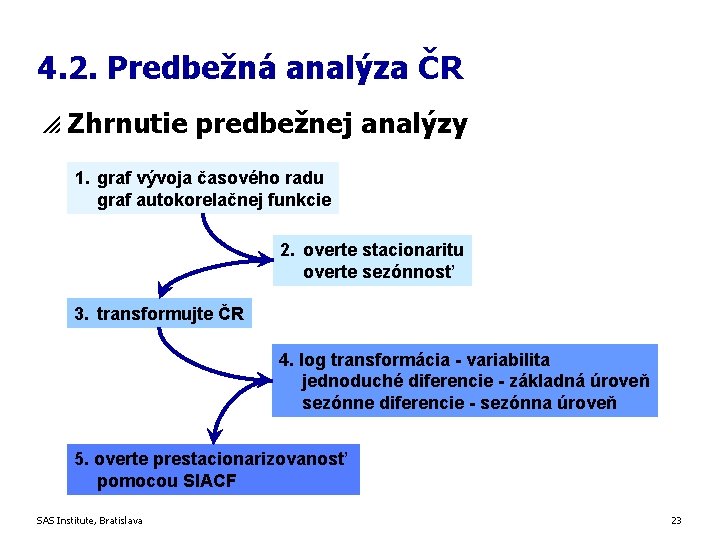
4. 2. Predbežná analýza ČR p Zhrnutie predbežnej analýzy 1. graf vývoja časového radu graf autokorelačnej funkcie 2. overte stacionaritu overte sezónnosť 3. transformujte ČR 4. log transformácia - variabilita jednoduché diferencie - základná úroveň sezónne diferencie - sezónna úroveň 5. overte prestacionarizovanosť pomocou SIACF SAS Institute, Bratislava 23

Ukážka Predbežná analýza ČR SAS Institute, Bratislava