Modely asovch radov s dlhou pamou ARFIMA modely

Modely časových radov s dlhou pamäťou – ARFIMA modely 1

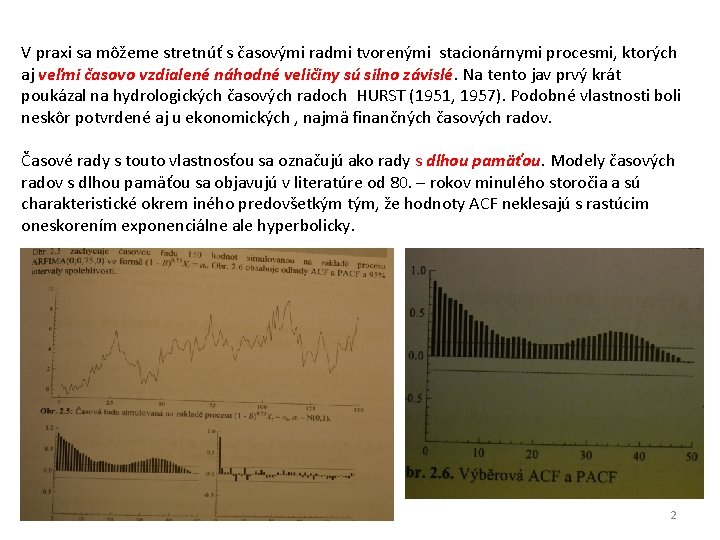
V praxi sa môžeme stretnúť s časovými radmi tvorenými stacionárnymi procesmi, ktorých aj veľmi časovo vzdialené náhodné veličiny sú silno závislé. Na tento jav prvý krát poukázal na hydrologických časových radoch HURST (1951, 1957). Podobné vlastnosti boli neskôr potvrdené aj u ekonomických , najmä finančných časových radov. Časové rady s touto vlastnosťou sa označujú ako rady s dlhou pamäťou. Modely časových radov s dlhou pamäťou sa objavujú v literatúre od 80. – rokov minulého storočia a sú charakteristické okrem iného predovšetkým tým, že hodnoty ACF neklesajú s rastúcim oneskorením exponenciálne ale hyperbolicky. 2

Časové rady s touto vlastnosťou nazývame rady s dlhou pamäťou (generujú ich stochastické procesy, procesy ktoré nazývame procesy s dlhou pamäťou). pamäťou Ich charakteristickou vlastnosťou je, že hodnoty ACF neklesajú s rastúcim oneskorením exponenciálne, ale hyperbolicky. Frakcionálne integrované procesy rádu „d“ definovali a jeho vlastnosti odvodili GRANGER (1980), GRANGER JOYEX(1980) a HOSKING (1981), má formu (1. ) kde at je proces bieleho šumu a d nemusí byť celé číslo, označuje sa ako frakcionálny parameter a symbol potom vyjadruje frakcionálnu diferenciu. Modely s neceločíselným d sa nazývajú frakcionálne integrované procesy rádu d autoregresná reprezentácia nekonečného radu frakcionálne integrovaného procesu má tvar (2. ) (3. ) 3

(4. ) kde Γ(z) je gama funkcia: (5. ) Vzhľadom k tomu, že pre gama funkciu platí: (k – d) = ((k – d – 1) (k – d – 2) …, (2 – d) (1 – d) (-d)) (– d) (6. ) Je možné autoregresný koeficient vyjadriť takto: (7. ) 4

Frakcionálne integrovaný proces je možné vyjadriť vo forme reprezentácie kĺzavých priemerov nekonečného rádu: (8. ) Kde parametre sú získané z rovnice rozvoja: (9. ) Pretože (10. ) môžeme písať: (11. ) 5

(12. ) Parciálna autokorelačná funkcia frakcionálne integrovaného procesu rádu d: (13. ) Zaujímavé sú asymptotické aproximácie uvedených parametrov procesov s použitím STIRLINGOVEJ aproximácie pre vysoké k vo forme: (14. ) Potom môžeme odvodiť parametre (15. ) 6

(16. ) 7

Uvažujme proces ARIMA(0, d, 0). Pre | d | < 0, 5 platí: • 1. {Yt} je proces stacionárny a invertibilný • 2. ACF má tvar (17. ) t. j. pre k , takže pre 0 < d < 0, 5 je (k) > 0 a s rastúcim posunutím k klesá ACF monotónne a hyperbolicky k 0 (tento pokles je omnoho pomalší ako pre d = 0). 3. PACF je daná vzťahom , (18. ) k = 1, 2, . . Jej pokles je určený číslom k-1, ktoré nezávisí od d. 8

Proces ARIMA(0, d, 0) je pre: 0 < d < 0. 5 proces s dlhou pamäťou ( | (k)| ) -0. 5 < d < 0 proces so strednou pamäťou ( | (k)| konšt. ) d 0. 5 nestacionárny proces d -0. 5 neinvertibilný proces d < 0. 5 stacionárny proces d > -0. 5 invertibilný proces Kombináciou frakcionálneho diferencovania a procesu ARMA(p, q) sa získa trieda procesov ARFIMA(p, d, q). Dôležitou vlastnosťou týchto procesov je, že vplyv parametra d na vzdialené premenné s rastúcim oneskorením klesá hyperbolicky, hyperbolicky ale vplyv AR a MA parametrov klesá exponenciálne; exponenciálne d teda charakterizuje korelačnú štruktúru pre veľké oneskorenia, oneskorenia ostatné parametre charakterizujú korelačnú štruktúru v malých oneskoreniach Aj keď je ARFIMA(p, d, q) pre 0. 5 < d < 1 nestacionárny proces, vygenerované časové rady sú priťahované k strednej hodnote procesu. 9

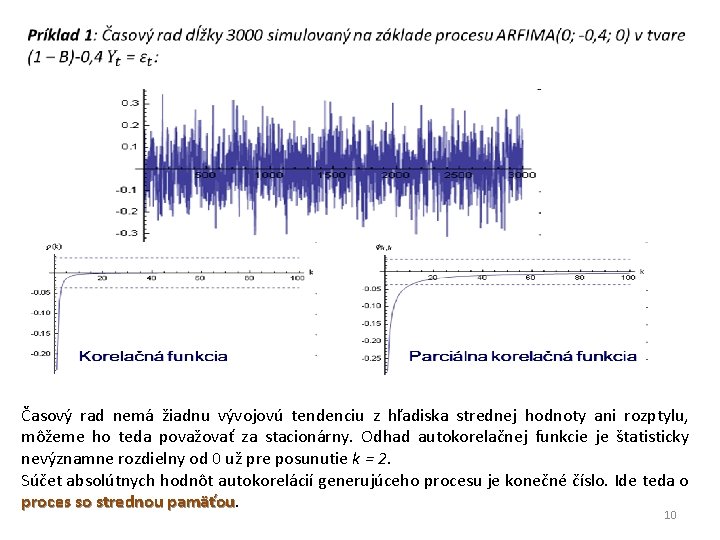
Časový rad nemá žiadnu vývojovú tendenciu z hľadiska strednej hodnoty ani rozptylu, môžeme ho teda považovať za stacionárny. Odhad autokorelačnej funkcie je štatisticky nevýznamne rozdielny od 0 už pre posunutie k = 2. Súčet absolútnych hodnôt autokorelácií generujúceho procesu je konečné číslo. Ide teda o proces so strednou pamäťou 10

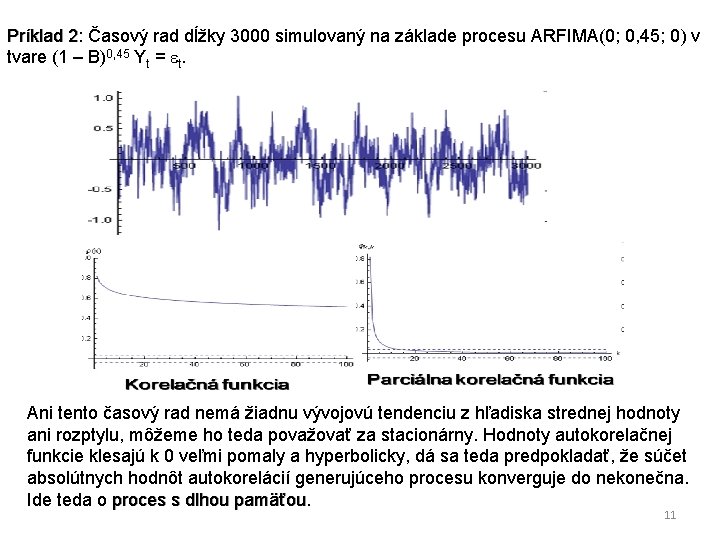
Príklad 2: 2 Časový rad dĺžky 3000 simulovaný na základe procesu ARFIMA(0; 0, 45; 0) v tvare (1 – B)0, 45 Yt = t. Ani tento časový rad nemá žiadnu vývojovú tendenciu z hľadiska strednej hodnoty ani rozptylu, môžeme ho teda považovať za stacionárny. Hodnoty autokorelačnej funkcie klesajú k 0 veľmi pomaly a hyperbolicky, dá sa teda predpokladať, že súčet absolútnych hodnôt autokorelácií generujúceho procesu konverguje do nekonečna. Ide teda o proces s dlhou pamäťou 11

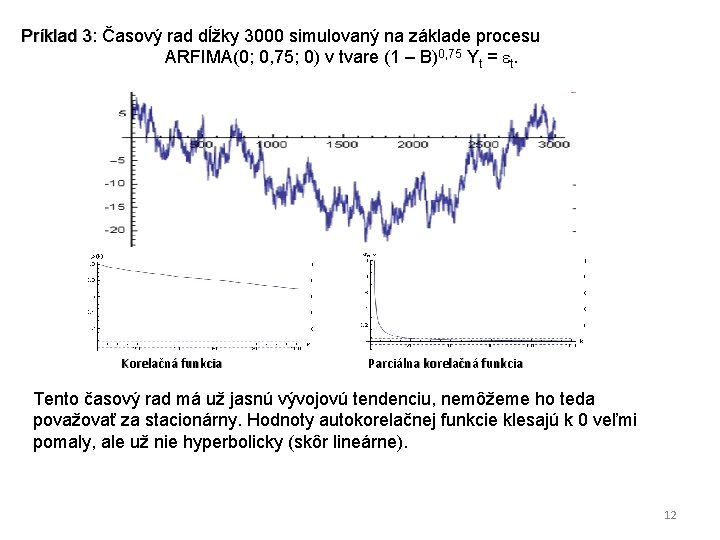
Príklad 3: 3 Časový rad dĺžky 3000 simulovaný na základe procesu ARFIMA(0; 0, 75; 0) v tvare (1 – B)0, 75 Yt = t. Korelačná funkcia Parciálna korelačná funkcia Tento časový rad má už jasnú vývojovú tendenciu, nemôžeme ho teda považovať za stacionárny. Hodnoty autokorelačnej funkcie klesajú k 0 veľmi pomaly, ale už nie hyperbolicky (skôr lineárne). 12

Testovanie hypotézy pre modely s dlhou pamäťou Uvažujme proces Yt = + t, kde t = 1, …, n je ľubovoľný parameter t je stochastický proces s nulovou strednou hodnotou. 13

Používajú sa dve testovacie štatistiky. Pri prvej sa najprv vypočíta výraz: (19. ) Potom sa vypočíta testovacia štatistika Vm: (20. ) Ak vypočítaná hodnota testovacej štatistiky patrí do intervalu (0. 809; 1. 862), na hladine významnosti = 0, 05 nemôžeme zamietnuť nulovú hypotézu, že proces má len krátku pamäť. Ak je však hodnota mimo tohto intervalu, neznamená to ešte jednoznačne, že proces má dlhú pamäť. Potvrdíme (alebo vyvrátime) tento predpoklad použitím ďalšej testovacej štatistiky. 14

Najprv vypočítame výraz (odporúčané hodnoty q pre n > 125 sú n/10 a n/5) : (21. ) Opäť vypočítame hodnotu normovanej testovacej štatistiky číslo dva: (22. ) Ak je vypočítaná hodnota testovacej štatistiky mimo intervalu (0, 809; 1, 862), na hladine významnosti α = 0, 05 zamietame nulovú hypotézu, že proces má len krátku pamäť. 15

Príklad 1: 1 Časový rad dĺžky 3000 simulovaný na základe procesu ARFIMA(0; -0, 4; 0) v tvare (1 – B)-0, 4 Yt = t. Prvá testovacia štatistika: Hodnota testovacej štatistiky je mimo (0, 809; 1, 862). Vypočítame preto aj druhú testovaciu štatistiku. Vypočítané hodnoty testovacej štatistiky sú (až na jednu) mimo (0. 809; 1. 862). Na hladine významnosti α = 0. 05 zamietame nulovú hypotézu, že proces má len krátku pamäť. 16

Príklad 2: 2 Časový rad dĺžky 3000 simulovaný na základe procesu ARFIMA(0; 0, 45; 0) v tvare (1 – B)0, 45 Yt = t. Prvá testovacia štatistika: Hodnota testovacej štatistiky je mimo (0. 809; 1. 862). Vypočítame preto aj druhú testovaciu štatistiku. Vypočítané hodnoty testovacej štatistiky sú mimo (0. 809; 1. 862). Na hladine významnosti = 0. 05 zamietame nulovú hypotézu, že proces má len krátku pamäť. 17

Príklad 3: 3 Časový rad dĺžky 3000 simulovaný na základe procesu ARFIMA(0; 0, 75; 0) v tvare (1 – B)0, 75 Yt = t. Prvá testovacia štatistika: Vypočítaná hodnota testovacej štatistiky je mimo (0. 809; 1. 862). Neznamená to jednoznačne, že proces má dlhú pamäť. Potvrdíme (alebo vyvrátime) tento predpoklad použitím druhej testovacej štatistiky. Dve hodnoty testovacej štatistiky sú mimo a dve v (0. 809; 1. 862). Na hladine významnosti = 0. 05 nevieme rozhodnúť, či má proces len krátku pamäť. 18

Odhad parametrov modelov ARFIMA Odhad parametrov pri modeloch ARFIMA je podstatne komplikovanejší ako pri modeloch ARMA. Neceločíselný parameter d má v porovnaní s ostatnými parametrami špecifický význam, pretože podľa jeho hodnoty je možné určiť, či ide o proces s dlhou alebo krátkou pamäťou, stacionárny alebo nestacionárny. Existujú dve skupiny metód na odhad parametrov modelov ARFIMA. Prvú skupinu tvoria dvojkrokové metódy: najprv sa odhadne parameter d a potom sa odhadnú parametre modelu ARMA pre transformovaný časový rad (filtrovaný frakcionálnym diferencovaním pre vypočítaný parameter d). Tieto metódy sú použiteľné len pre dostatočne dlhé časové rady. Druhú skupinu tvoria jednokrokové metódy, v ktorých sa súčasne odhadnú všetky parametre modelu ARFIMA. Väčšina z nich je založená na rôznych variantoch metódy maximálnej vierohodnosti či už v časovej alebo vo frekvenčnej oblasti. Hlavným nedostatkom týchto metód je ich výpočtová zložitosť, nutnosť poznať počiatočné hodnoty pre jednotlivé parametre a možná existencia lokálneho extrému funkcie vierohodnosti. 19

1. Dvojkrokové metódy 1. 1 Hurstov koeficient. Najprv musíme rozdeliť časový rad do m spojitých úsekov dĺžky N, pričom m x N = n (celková dĺžka časového radu). Pre každý tento j-ty úsek (j = 1, …, m): 1. Vypočítame aritmetický priemer (označíme ho Ej) a smerodajnú odchýlku Sj 2. Centrujeme dáta odčítaním aritmetického priemeru Xi, j = Yi, j - Ej pre i = 1, …, N (23. ) 3. Vytvoríme kumulatívny časový rad postupným sčítaním po sebe idúcich centrovaných premenných: (24. ) 4. Určíme rozsah kumulatívneho časového radu odčítaním minimálnej hodnoty od maximálnej, čím získame štatistiku Rj: Rj = max (Z 1, j, …, ZN, j) - min (Z 1, j, …, ZN, j) 5. Vydelíme rozsah Rj smerodajnou odchýlkou Sj (reškálovaný rozsah) 6. Vypočítame priemer reškálovaných rozsahov pre všetky úseky dĺžky N: (25. ) 20

7. Dĺžku úseku N zväčšíme na najbližšie číslo, pre ktoré existuje také celé číslo m, že m x N = n. Kroky 1 - 7 opakujeme, pokiaľ N n/2. 8. Hurstov koeficient H, pre ktorý platí H = d + 0. 5 odhadneme ako regresný parameter v lineárnej regresii, kde závisle premenná je a nezávisle premenná je ln(N): Aby sme dostali korektný odhad Hurstovho koeficientu H, musí byť v regresii minimálne 10 bodov. 21

1. 2 Semiparametrický odhad d Táto metóda je založená na odhade parametra d vo frekvenčnej oblasti. Vychádza z teórie lineárnych filtrov, ktorá umožní vyjadriť proces (1 - B)d Yt = t v tvare fy( ) = | 1 - e-i | -2 d f ( ), kde fy( ) a f ( ) sú spektrálne hustoty procesov Yt a t. Po úprave môžeme písať (v spojitom tvare): (26. ) v diskrétnom tvare: (27. ) Odhad parametra d sa získa z lineárnej regresie vychádzajúcej z predchádzajúcej rovnice pre rôzne frekvencie 1, 2, …, N: (28. ) Predpokladá sa, že uj sú nezávislé rovnako rozdelené náhodné premenné s nulovou strednou hodnotou a rozptylom 2/6. Ak je {uj} proces bieleho šumu, regresiou sa získa dobrý odhad parametra d. Ak sú náhodné premenné autokorelované, platí vzťah regresie len pre frekvencie blízke 0 len v tomto prípade je odhad d konzistentný. Základnou otázkou v prípade korelovaných uj je teda určenie čísla N(napr. N , resp. sa volí také N, aby bol reziduálny rozptyl regresie rovný približne 2/6). 22

Na testovanie parametra d sa používa štandardný t-test. Napriek tomu, že semiparametrický odhad parametra d je veľmi jednoduchý, nejasnosti spojené s určením čísla N pri silnej autokorelácii procesu {uj} znižujú jeho atraktívnosť. Pri nevhodnej voľbe N môžeme totiž získať veľmi vychýlený odhad. Preto sa stále častejšie v praxi používajú jednokrokové metódy. 23

2. Jednokrokové metódy 2. 1 Metóda maximálnej vierohodnosti Táto metóda je určená k odhadu parametrov modelu ARFIMA v tvare: p(B) (1 - B)d Yt = q(B) t za predpokladu, že t sú nezávislé náhodné premenné s rovnakým normálnym rozdelením pravdepodobnosti. Potom logaritmus presnej vierohodnostnej funkcie má po uprave tvar: (29. ) kde je vektor parametrov modelu AR, je vektor parametrov modelu MA, Y je stĺpcový vektor náhodných premenných typu n x 1. Maximalizáciou tejto funkcie získame maximálne vierohodné odhady parametrov d, , . Hlavným problémom pri tejto metóde je výpočet autokorelačnej matice Pn a jej invertovanie. Boli vyvinuté mnohé iteračné metódy, ktoré okrem odhadov počítajú aj ich smerodajné chyby, potrebné k t-testom. 24