11 Trigonometry Trigonometry is derived from Greek words



























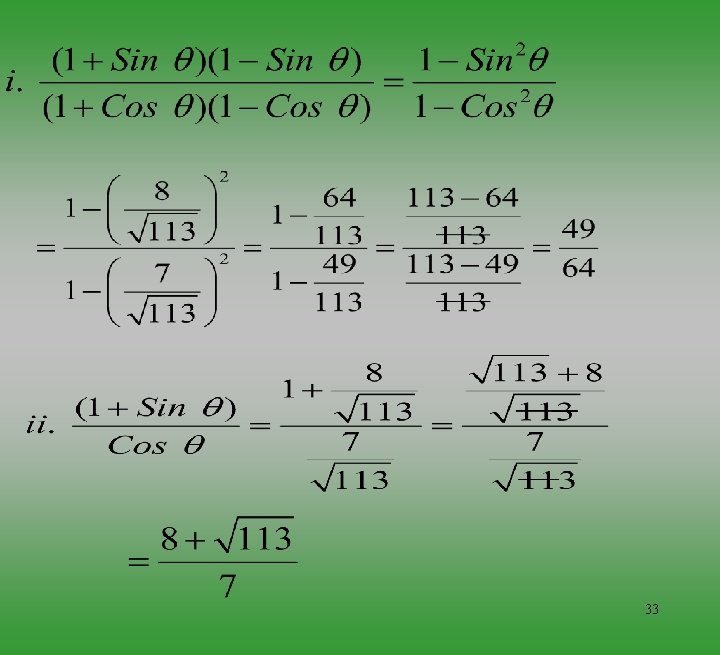























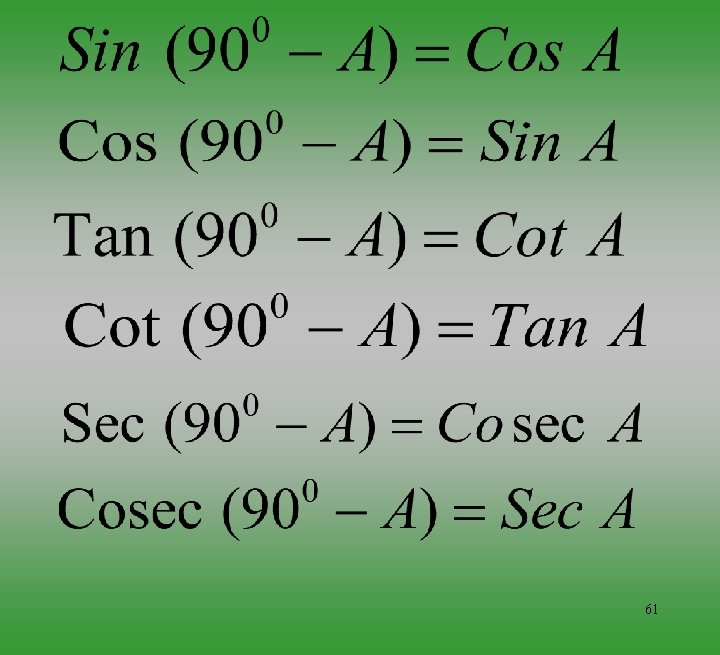





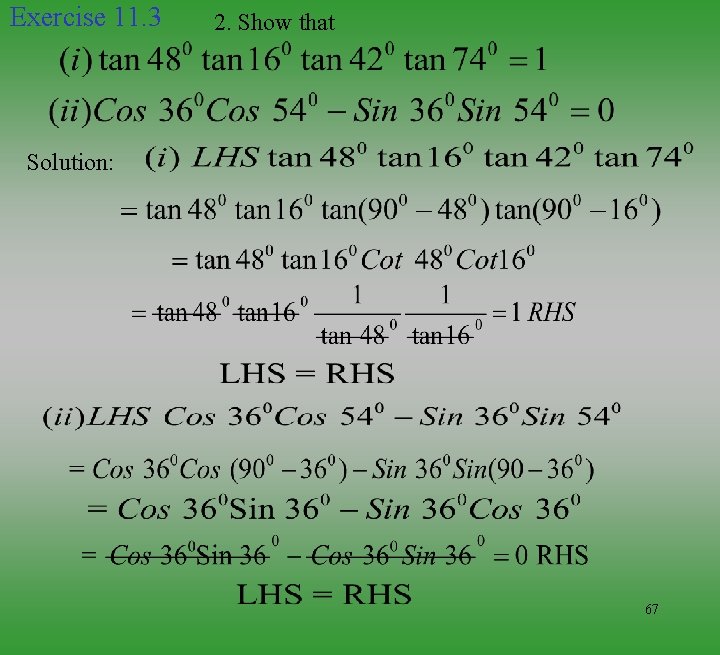







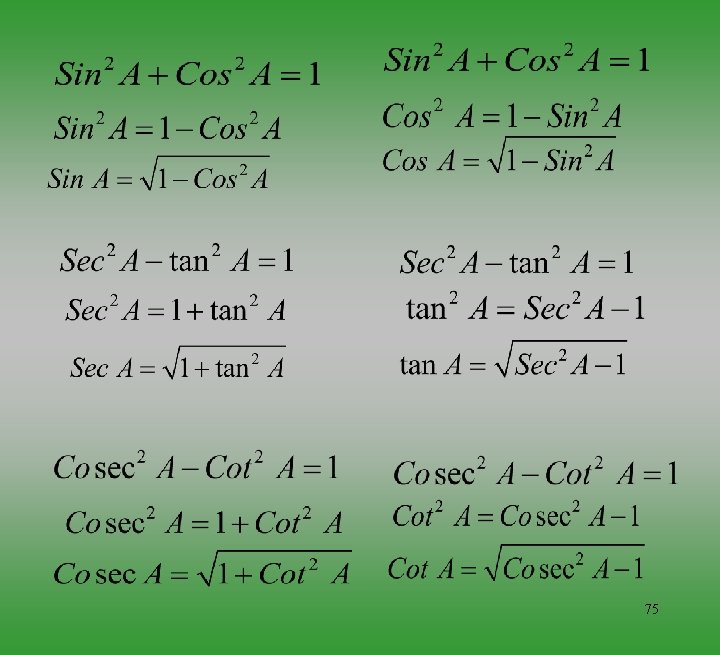





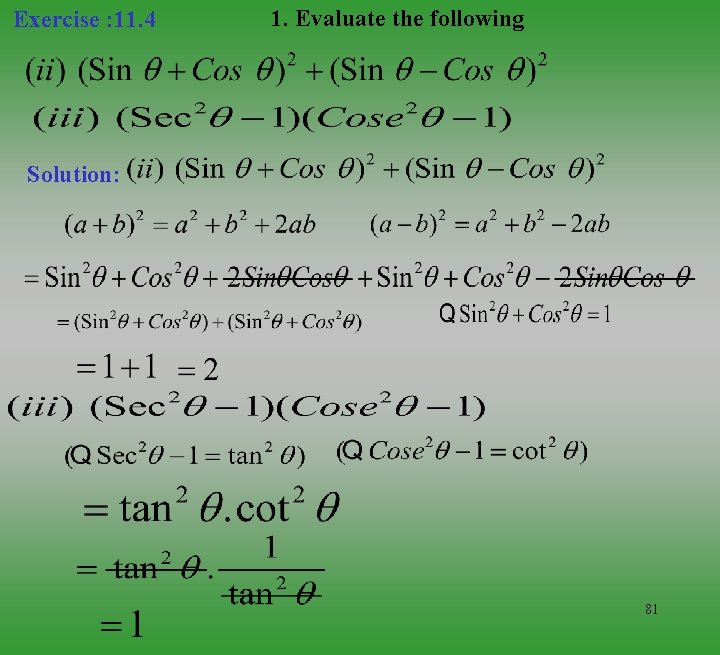
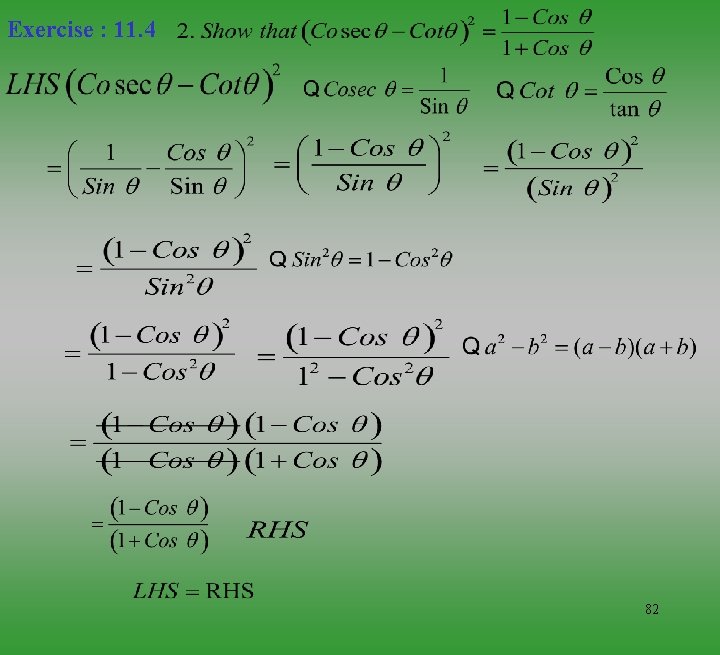




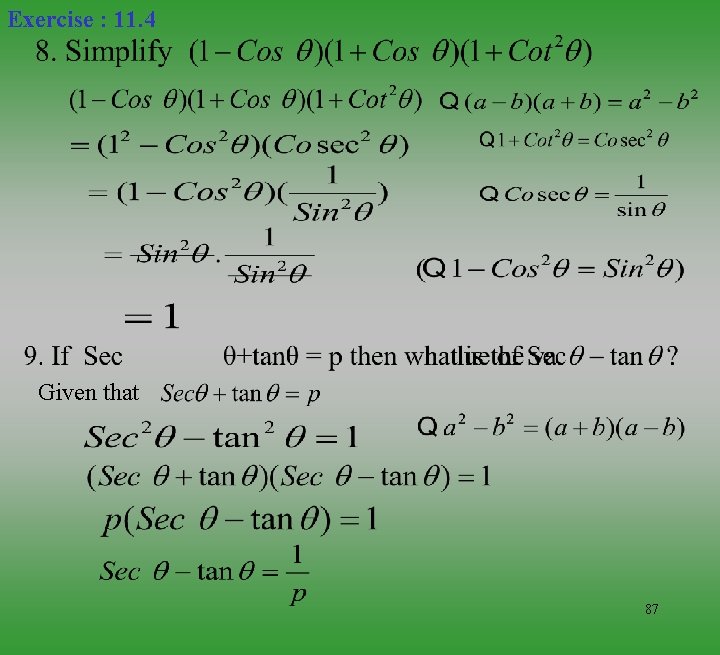






- Slides: 95

( 11. Trigonometry ) Trigonometry is derived from Greek words tri ( three) gonon (angles) and metron ( measure). Trigonometry means the measure of three angles in a right triangle. Trigonometry specifically deals with the relationships between the sides and the angles of triangles, that is, on the trigonometric functions, and with calculations based on these functions. 1

If an angle of a triangle contains 900 , then that triangle said to be right angle triangle. 900 An angle which contains then that angle is said to be right angle. e s nu te o p hy Opposite side Relations between sides and angles of a right triangle Adjecent Side The side which is opposite to right angle is called hypotenuse. It denote by AB or c. The side opposite to an angle is called opposite side to and it is denoted by BC or a. The side adjacent to an angle is called adjacent side to and it is denoted by AC or b. 2

Ratioes of a right triangle. Opposite side to A / hypotenuse e us n te o p hy Opposite side The ratio of opposite side and hypotenuse is called Sine A. Shortly it is written as Sin A and read as Sine A. Adjacent side The ratio of adjacent side and hypotenuse is called Cosine A. Shortly it is written as Cos A and read as Cos A adjacent side to A / hypotenuse 3

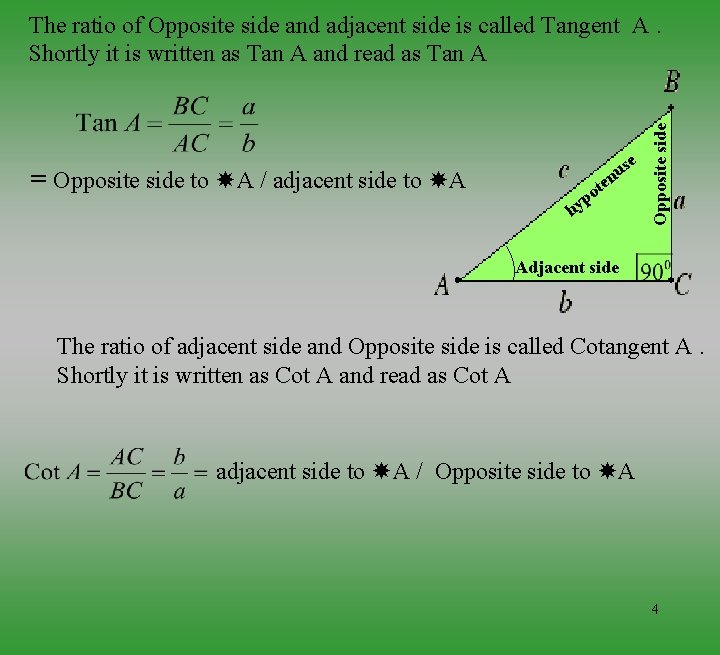
= Opposite side to A / adjacent side to A s nu e e t po hy Opposite side The ratio of Opposite side and adjacent side is called Tangent A. Shortly it is written as Tan A and read as Tan A Adjacent side The ratio of adjacent side and Opposite side is called Cotangent A. Shortly it is written as Cot A and read as Cot A adjacent side to A / Opposite side to A 4

= hypotenuse / adjacent side to A se u ten o p hy Opposite Side The ratio of hypotenuse and adjacent side is called Secant A. Shortly it is written as Sec A and read as Sec A Adjacent Side The ratio of hypotenuse and Opposite side is called Secant A. Shortly it is written as Cosec A or csc A and read as Cosec A = hypotenuse / Opposite side to A 5

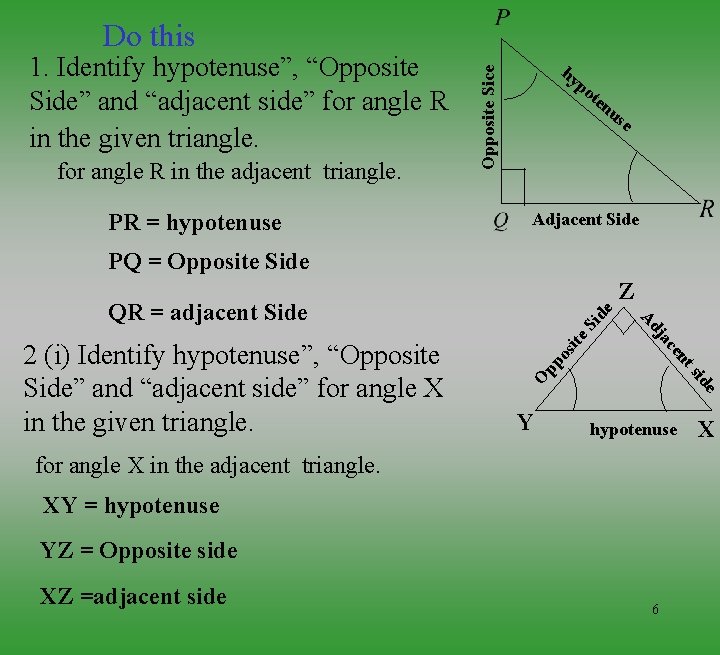
Do this for angle R in the adjacent triangle. PR = hypotenuse hy p Opposite Sice 1. Identify hypotenuse”, “Opposite Side” and “adjacent side” for angle R in the given triangle. ot e nu se Adjacent Side PQ = Opposite Side Z Si de ite os Y e sid O pp nt 2 (i) Identify hypotenuse”, “Opposite Side” and “adjacent side” for angle X in the given triangle. ce ja Ad QR = adjacent Side hypotenuse for angle X in the adjacent triangle. XY = hypotenuse YZ = Opposite side XZ =adjacent side 6 X

Do this e sid nt ce ja Ad e for angle Y in the adjacent triangle. Z it os pp OO e sid 2 (i) Identify hypotenuse”, “Opposite Side” and “adjacent side” for angle Y in the given triangle. Y X hypotenuse XY = hypotenuse XZ = Opposite Side YZ = adjecent Side 7

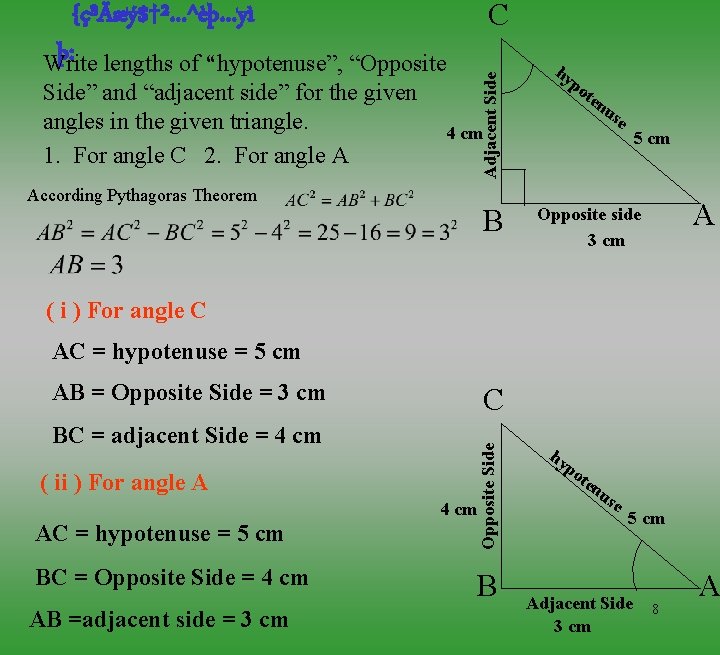
C Side” and “adjacent side” for the given angles in the given triangle. 1. For angle C 2. For angle A Adjacent Side {ç³Äæý$†²…^èþ…yì þ: lengths of “hypotenuse”, “Opposite Write hy po ten us 4 cm According Pythagoras Theorem B e 5 cm A Opposite side 3 cm ( i ) For angle C AC = hypotenuse = 5 cm AB = Opposite Side = 3 cm BC = adjacent Side = 4 cm ( ii ) For angle A 4 cm AC = hypotenuse = 5 cm BC = Opposite Side = 4 cm AB =adjacent side = 3 cm Opposite Side C B hy po ten us e 5 cm Adjacent Side 3 cm 8 A

Do This 13 c m 5 cm 1. Find (i) Sin C (ii) Cos C and (iii) tan C in the adjacent triangle. In the adjacent Δ ABC , B = 900 According Pythagoras Theorem 12 cm cm 9

In triangle XYZ , Y is right angle. XZ= 17 cm and YZ=15 cm then find (i) sin X (ii) Cos Z (iii ) tan X. In triangle XYZ , Y is right angle. According Pythagoras Theorem X 17 8 cm Do this Y cm Z 15 cm XY = 8 cm 10

In triangle PQR with right angle at Q , the value of P is x , PQ = 7 cm and QR = 24 cm, then find Sin x and Cos x. In triangle PQR with right angle at Q According Pythagoras Theorem P 25 cm 7 cm Do This Q R 24 cm PR = 25 cm 11

A In a right angle triangle ABC , right angle is at C. BC+CA= 23 cm and BC – CA = 7 cm, then find Sin A and Tan B. In a right angle triangle ABC , right angle is at C. 17 cm 8 cm Try This C B 15 cm In ΔABC , C = 900 According Pythagoras Theorem AB = 17 cm 12

Think - Discuss (i) deos exists for some value of angle x ? Sin value exists always less than 1. Value is more than 1. So it does not exists for some value of angle x. (ii) The Value of Sin A and Cos A is always less than 1. Why? Origin is the centre of the circle and radius is 1 unit. P(a, b) is the point on the circle. The point is making an angle with A. Y Coordinate X Coordinate 13

P is making an angle 3600 at centre to rotate one complete revolution. In adjacent figure AOB is the one fourth part of revolution and making an angle of 900. AOC is the half part of revolution which makes an angle of 1800 at centre of the circle. AOD is the three fourth part of revolution which makes 2700 at the centre. A, B, C, D points are the ordered pairs which are (1, 0), ((0, 1), (-1, 0), (0, -1) respectively. According to the Ordered Pairs Sin 00 = 0 Sin 900 = 1 Sin 1800 = 0 Cos 00 = 1 Cos 900 = 0 Cos 1800 = – 1 Sin 2700 = – 1 Cos 2700 = 0 Sin 3600 = 0 Cos 3600 = 1 Like this Sine and Cosine Values are always exists less than 1. (iii) Tan A is the product of tan and A. Tan A means Value of the Tangent of an angle A. But not the product of tan and A. 14

Multiplicative Inverses of Trigonometrical Ratioes Opposite Side Opposite side of A / hypotenuse e = hypotenuse / Opposite side of A us n te o p hy Adjacent Side So Sine and Cosec are called multiplicative inverse trigonometrical ratioes of each other. 15

Multiplicative Inverses of Trigonometrical Ratioes = hypotenuse / Adjacent side of A e us n te o p hy Adjacent Side Opposite Side Adjacent side of A / hypotenuse So Cosine (Cos) and Secant (Sec) are called multiplicative inverse trigonometrical ratioes of each other. 16

Multiplicative Inverses of Trigonometrical Ratioes se u ten adjacent side of A / Opposite side of A o p hy Opposite Side = Opposite side of A / adjacent side of A Adjacent Side So Tangent ( Tan ) and Cotangent ( Cot ) are called multiplicative inverse trigonometrical ratioes of each other. 17

e us n te o p hy Opposite side Ratioes of trigonometrical Ratioes. Adjacent Side = Opposite side of A / adjacent side of A 18

e us n te o p hy Adjacent Side Opposite Side Ratioes of trigonometrical Ratioes. adjacent side of A / Opposite side of A 19

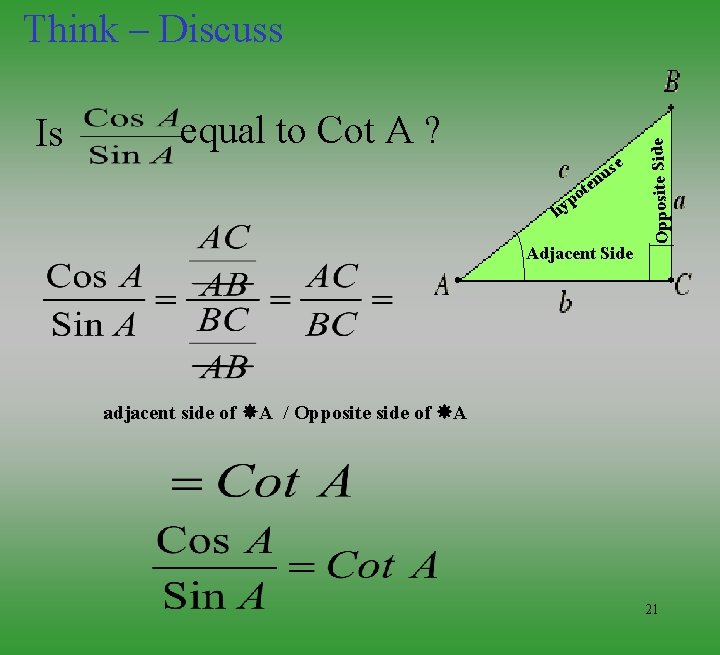
e us n te o p hy Adjacent Side Opposite Side Is Think – Discuss equal to Tan A ? = Opposite side of A / adjacent side of A 20

Is equal to Cot A ? se u ten o p hy Adjacent Side Opposite Side Think – Discuss adjacent side of A / Opposite side of A 21

Example: 1 then find the other trigonometric ratio of angle A. = Opposite side of A / adjacent side of A Opposite side : adjacent side = 3: 4 Opposite Side of A = BC = 3 k ( where k is any positive number ) A adjacent side of A = AB = 4 k C us n k 5 pote hy e Adjacent Side 4 k Opposite Side If 3 k B According to Pythagoras theorem in Δ ABC AC 2 = AB 2+BC 2 AC 2 = (3 k)2+(4 k)2 = 9 k 2+16 k 2 = 25 k 2 = (5 k)2 AC = 5 k 22

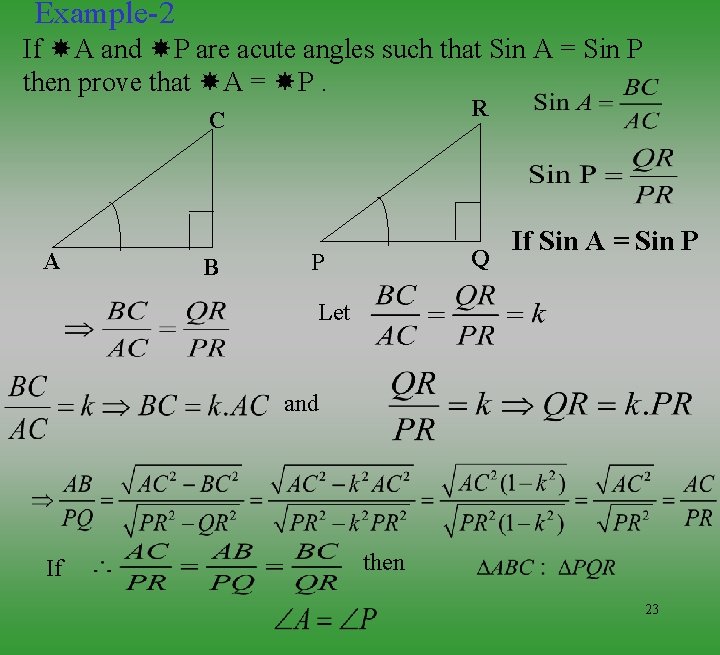
Example-2 If A and P are acute angles such that Sin A = Sin P then prove that A = P. R C A B Q P If Sin A = Sin P Let and If then 23

Another Method of Example-2 If A and P are acute angles such that Sin A = Sin P then prove that A = P. P In ΔACP , Given that Sin A = Sin P þ For angle A in ΔACP For angle P in ΔACP A C 24

PR = 20 Q ts 29 i un 20 units 21 units Example : 3 Consider a triangle PQR , right angled at P in which PQ = 29 units , QR= 21 units and PQR = then find the value of and According to Pythagoras theorem in P Δ PQR PR 2 = PQ 2 - QR 2 R units 25

Exercise – 11. 1 C m c 7 15 cm 1. In a right angle triangle ABC, 8 cm , 15 cm and 2. 17 cm are the lengths of AB, BC and CA 3. respectively. Then find out Sin A , Cos A 4. Given and A =. 8 cm ; BC = 15 cm ; thattan , AB CA = 17 Cm in a right angle triangle ABC. A 1 8 cm B CA is the longest side of a right angle triangle ABC. Hence CA is the hypotenuse of a ΔABC. For angle A Sin A = Opposite side to A/ hypotenuse = Cos A = Adjacent side to A/ hypotenuse = tan A = Opposite side to A / Adjacent side to A = 26

Solution : Given that in ΔPQR , Q = 900 , PQ = 7 cm , PR = 25 cm. 24 cm Exercise – 11. 1 2. The sides of a right angle triangle PQR are PQ = 7 cm , QR = 25 R cm and Q = 900 respectively. Then Find tan Q – tan R. m c 5 2 P 7 cm Q According to Pythagoras theorem in ΔPQR QR 2 = PR 2 - PQ 2 = 252 - 72 =625 -49 = 576=242 QR = 24 cm For angle P ; tan P = Opposite side to P / Adjacent side to P = For angle R ; tan R = Opposite side to P / Adjacent side to P = 27

Exercise – 11. 1 3. In a right angle triangle ABC with right angle at B, in which a = 24 units , b = 25 units and BAC = . Then find cos and tan . C s a = 24 units b= nit u 5 2 A 7 units B Solution : Given that , in ΔABC B = 900 a = BC= 24 units , b = AC = 25 units and BAC = . According to Pythagoras theorem in ΔABC AB 2 = AC 2 - BC 2 = 252 - 242 =625 -576 = 49=72 AB = 7 units Cos = Adjacent side to / hypotenuse = tan = Opposite side to / Adjacent side to = 28

Exercise – 11. 1 Solution : Let in triangle ΔABC , B = Cos A = 12/13 900 A Cos A = 12/13 = Adjacent side to A/ hypotenuse Adjacent side : hypotenuse = 12: 13 5 k C k 13 12 k B Adjacent side to A = AB =12 k ( where k is any positive number ) hypotenuse = AC =13 k According to Pythagoras theorem in ΔABC BC 2 = AC 2 - AB 2 = (13 k)2 – (12 k)2 =169 k 2 -144 k 2 = 25 k 2 =(5 k)2 BC = 5 k Sin A = Opposite side to A / hypotenuse = tan A = Opposite side to A / adjacent side to A = 29

Exercise – 11. 1 5. If 3 tan A = 4 then find Sin A and Cos A. C tan A = 4 / 3 = Opposite side to A / adjacent side to A 4 k Solution : Given that , 3 tan A = 4 5 k Opposite side : adjacent side = 4: 3 B 3 k A Opposite side to A = BC =4 k ( where k be any positive number ) Adjacent side to A = AB =3 k According to Pythagoras theorem in ΔABC AC 2 = AB 2 + BC 2 = (3 k)2 + (4 k)2 =9 k 2 + 16 k 2 = 25 k 2 =(5 k)2 AC = 5 k Sin A = Opposite side to A / hypotenuse = Cos A = adjacent side to A / hypotenuse = 30

Exercise – 11. 1 6. If A and X are acute angles such that Cos A = Cos X then show that A = X. X Given that , in triangle ΔACX Cos A = Cos X. For angle A in ΔACX A C For angle X in ΔACX 31

Exercise – 11. 1 8 k C Given that Cot = 7 / 8 = Adjacent side to / Opposite side to A Adjacent side : Opposite side = 7: 8 7 k B Adjacent side to = AB = 7 k ( Where k be any positive number) Opposite side to = BC =8 k According to Pythagoras theorem in ΔABC AC 2 = AB 2 + BC 2 = (7 k)2 + (8 k)2 = 49 k 2 + 64 k 2 = 113 k 2 = Sin = Opposite side to / hypotenuse = Cos = Adjacent side to / hypotenuse = 32
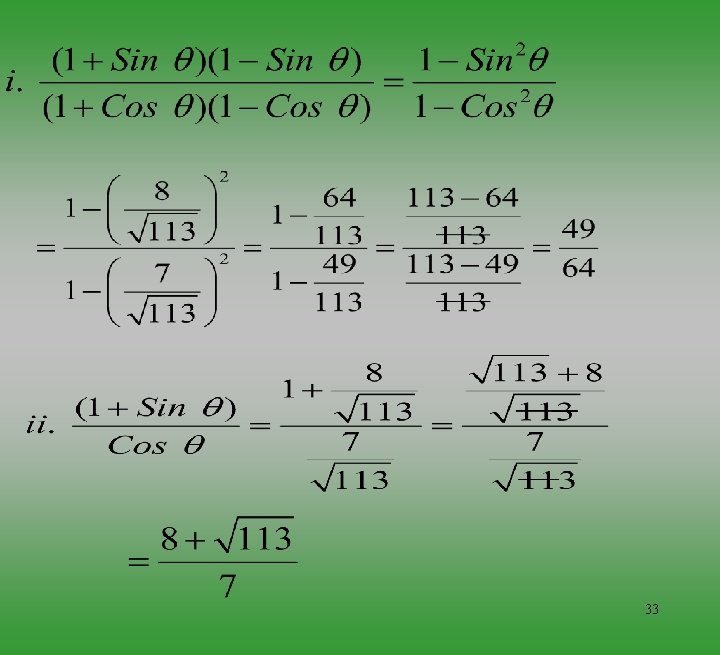
33

Exercise – 11. 1 8. In a right angle triangle ABC , right angle at B , if then find the values of i) Sin A Cos C+ Cos C Sin A ii) Cos A Cos C – Sin A Sin C Solution : Given that , in a right angle A triangle ABC , right angle at B and C k B = Opposite side to A / hypotenuse Opposite side : adjacent side = Opposite side to A = BC = ( where k be any positive number ) Adjacent side to A = AB =1 k = k According to Pythagoras theorem in ΔABC AC 2 = AB 2 + BC 2 = Sin A= Opposite side to A / hypotenuse = Sin C = Opposite side to C / hypotenuse = 34

Cos A= Adjacent side to A / hypotenuse = C Cos C= Adjacent side to C / hypotenuse = i) Sin A Cos C+ Cos C Sin A A k B ii) Cos A Cos C – Sin A Sin C 35

11. 3 Trigonometric Ratioes of Some Specific Angles C 11. 3. 1 Trigonometric Ratio of 450 In isosceles right angle triangle ABC , right angle at B A= C=450 and Let BC=AB = a By Pythagoras theorem in Δ ABC AC 2 = AB 2 + BC 2 = A B Sin 450 = Opposite side to 450 / hypotenuse = Cos 450 = Adjacent side to 450 / hypotenuse = Tan 450 = Opposite side to 450 / Adjacent side to 450 = Cot 450 = Adjacent side to 450 / Opposite side to 450 = Sec 450 = hypotenuse / Adjacent side to 450 = Cosec 450 = hypotenuse / Opposite side to 450 = 36

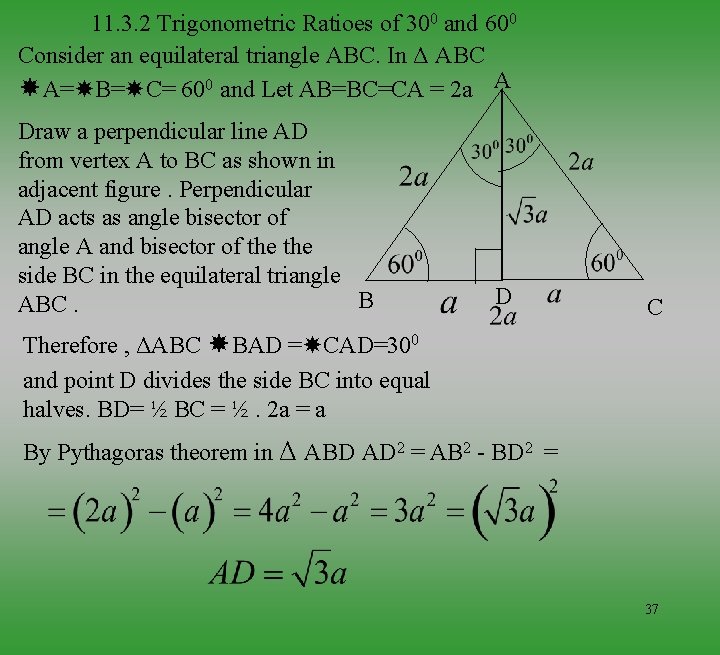
11. 3. 2 Trigonometric Ratioes of 300 and 600 Consider an equilateral triangle ABC. In Δ ABC A= B= C= 600 and Let AB=BC=CA = 2 a A Draw a perpendicular line AD from vertex A to BC as shown in adjacent figure. Perpendicular AD acts as angle bisector of angle A and bisector of the side BC in the equilateral triangle B ABC. D C Therefore , ΔABC BAD = CAD=300 and point D divides the side BC into equal halves. BD= ½ BC = ½. 2 a = a By Pythagoras theorem in Δ ABD AD 2 = AB 2 - BD 2 = 37

Sin 300 = Opposite side to 300 /hypotenuse Cos 300 = Adjacent side to 300 /hypotenuse A Tan 300 = Opposite side to 300 /Adjacent side to 300 B Cot 300 = Adjacent side to 300/ Opposite side to 300 D Sec 300 = hypotenuse / Adjacent side to 300 Cosec 300 = hypotenuse / opposite side to 300 38

Sin 600 = Opposite side to 600 / hypotenuse Cos 600 = Adjacent side to 600 A / hypotenuse Tan 600 = Opposite side to 600/ Adjacent side to 600 B D Cot 600 = Adjacent side to 600 / Opposite side to 600 Sec 600 = hypotenuse / Adjacent side to 600 Cosec 600 = hypotenuse / opposite side to 600 39

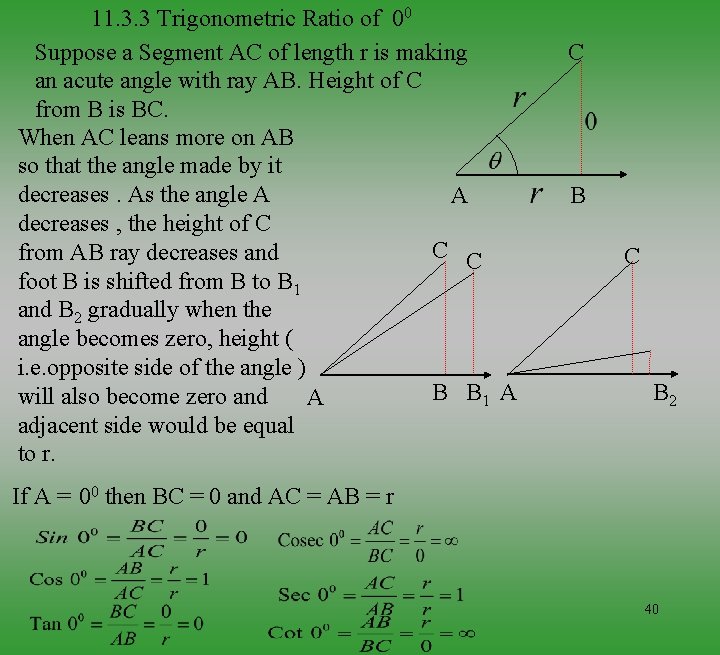
11. 3. 3 Trigonometric Ratio of 00 Suppose a Segment AC of length r is making an acute angle with ray AB. Height of C from B is BC. When AC leans more on AB so that the angle made by it decreases. As the angle A A decreases , the height of C C C from AB ray decreases and foot B is shifted from B to B 1 and B 2 gradually when the angle becomes zero, height ( i. e. opposite side of the angle ) B B 1 A will also become zero and A adjacent side would be equal to r. C B 2 If A = 00 then BC = 0 and AC = AB = r 40

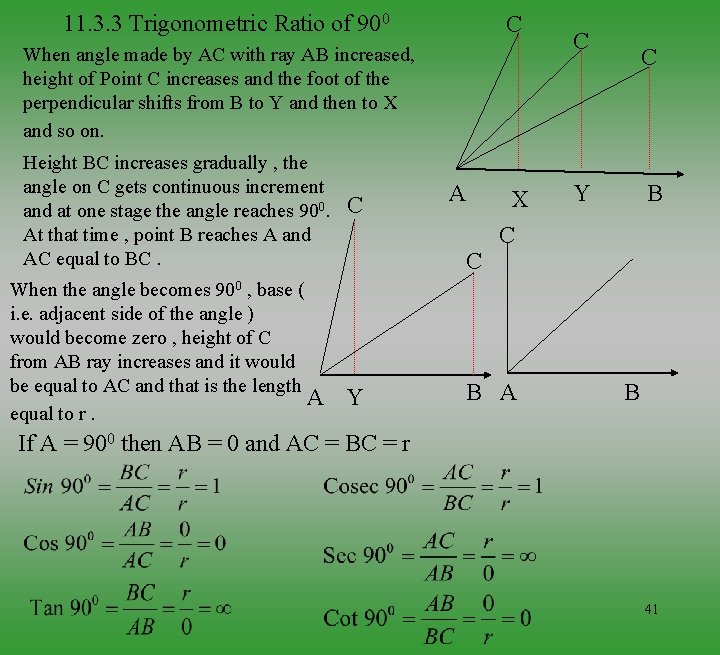
11. 3. 3 Trigonometric Ratio of 900 C When angle made by AC with ray AB increased, height of Point C increases and the foot of the perpendicular shifts from B to Y and then to X and so on. Height BC increases gradually , the angle on C gets continuous increment and at one stage the angle reaches 900. At that time , point B reaches A and AC equal to BC. When the angle becomes 900 , base ( i. e. adjacent side of the angle ) would become zero , height of C from AB ray increases and it would be equal to AC and that is the length A equal to r. C A C Y X C B A C C Y B B If A = 900 then AB = 0 and AC = BC = r 41

Do this Find Cosec 600 , Sec 600 and Cot 600. 42

Think – Discuss 1. What can you say about ? Is it defind ? Why? Reason : Division by zero is not Possible So it is not defined. 2. What can you say about ? Is it defind ? Why? Reason : Division by zero is not Possible So it is not defined. ? Why? 43

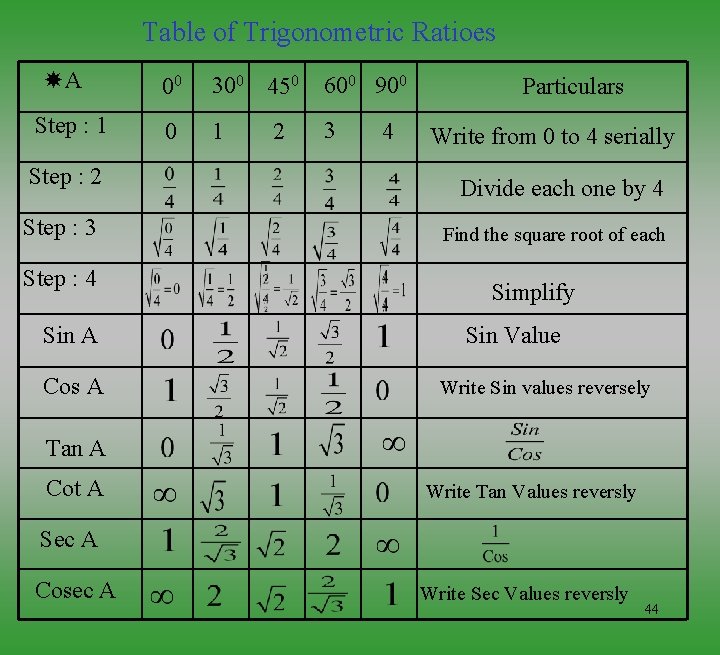
Table of Trigonometric Ratioes A Step : 1 Step : 2 Step : 3 Step : 4 Sin A Cos A 00 300 450 600 900 0 1 3 2 4 Particulars Write from 0 to 4 serially Divide each one by 4 Find the square root of each Simplify Sin Value Write Sin values reversely Tan A Cot A Write Tan Values reversly Sec A Cosec A Write Sec Values reversly 44

Think – Discuss What can you say about the value of Sin A and Cos A , as the value of angle A increases from 00 to 900? ( Observe the above table ) The Following table gives the evidence to say the given statement is true. If angle A increases then its sine values are also increases. A 00 300 450 600 900 Sin A Given statement is False. Because if value of angle A increases then its cos values are decreases. A 00 300 450 600 900 Cos A 45

Example - 4 Adjacent side to 300 = BC 5 cm In ΔABC, right angle is at B , AB= 5 cm and ACB=300 , Determine the lengths of the sides BC and AC. Solution: Given that in ΔABC, right angle at A B , AB = 5 cm and ACB=300 Opposite side to 300 = AB = 5 cm B C cm By using Pythagoras theorem in Δ ABC , AC 2 = AB 2 + BC 2 cm 46

Example- 5 Length of the chord AB = 2 BC=2(3)=6 cm Ü…. Ò$. 6ò . . Ò$ A Ü… COB= COA= 300 Length of the chord AB = 2 AC=2 BC 6ò A Chord of a circle of radius 6 cm is making an angle 600 at the centre. Find the length of the chord? Solution : Given that radius of the circle OA=OB=6 cm AOB = 600 OC is height from O upon AB and it is 0 angle bisector C B 47

Example: 6 In Δ PRQ, right angle is at Q , PQ = 3 cm and PR = 6 cm. Determine QPR and PRQ. P Q m 6 c 3 cm Solution : Given PQ = 3 cm and PR = 6 cm For the angle of R in ΔPQR R 48

Example : 7 A > B , Find A and B. 49

Exercise 11. 2 1. Evaluate the following 50

Exercise 11. 2 51

Exercise 11. 2 2. Choose the right option and justify your choice. ( (a) Sin 600 (b) Cos 600 (c) tan 300 c ) (d) Sin 300 52

Exercise 11. 2 2. Choose the right option and justify your choice. d ( (a) tan 900 (b) 1 (c) Sin 450 ( (a) Cos 600 (b) Sin 600 ) c (d) 0 ) (c) tan 600 (d) Sin 300 53

Exercise 11. 2 3. Evaluate Sin 600 cos 300 + cos 600 Sin 300. What is the value of Sin ( 600 + 300 ). What can you conclude ? Solution : Sin 600 cos 300 + Cos 600 Sin 300 …………. 1 Sin ( 600 + 300 ) = Sin 900 =1 …………. 2 From 1 and 2 Sin ( 600 + 300 ) = Sin 600 cos 300 + Cos 600 Sin 300 Sin ( A + B ) = Sin A cos B + Cos A Sin 300 54

Exercise 11. 2 4. Is it right to say Cos(600 + 300 ) = cos 600 Cos 300 – Sin 600 Sin 300 Solution : Cos 600 cos 300 – Sin 600 Sin 300 …………. 1 Cos ( 600 + 300 ) = Cos 900 = 0 …………. 2 From 1 and 2 0 0 Cos ( 600 + 300 ) = Cos 60 cos 30 – Sin 60 Sin 30 Therefore it is right to say Cos(600 + 300 ) = cos 600 Cos 300 – Sin 600 Sin 300 55

Exercise 11. 2 5. In a right angle triangle ΔPQR, right angle is at Q and PQ = 6 cm , RPQ = 600. Determine the lengths of QR and PR. P Q cm cm cm 6 cm 12 Solution : Given that right angle at Q in ΔPQR and PQ = 6 cm , RPQ = 600 For angle P in ΔPQR cm R 56

Exercise 11. 2 6. In ΔXYZ, right angle is at Y , YZ = x and XY = 2 x then determine YXZ and YZX Solution : In ΔXYZ , right angle is at Y , XZ = 2 x , XY = x X 4 x 2 = x 2 + YZ 2 = 4 x 2 – x 2 YZ 2 = 3 x 2 x (2 x)2 = (x)2 + YZ 2 2 x By using Pythagoras theorem XZ 2 = XY 2 + YZ 2 Y Z For angle Z in ΔXYZ For angle X in ΔXYZ 57

Exercise 11. 2 7. Is it right to say that Sin (A+B) = Sin A + Sin B ? Justify your answer Solution : Let A = 600 and B = 300 LHS Sin (A+B) = Sin (600 + 300 ) = Sin 900 = 1 RHS Sin A + Sin B = Sin 600 + Sin 300 = It is not right to say that Sin (A+B) = Sin A + Sin B 58

Think – Discuss For which value of acute angle For which value of Is true ? , above equation is not defined? Solution : For = 600 the given statement is true. 59

Trigonometric Ratioes of complementary Angles Two angles are said to be complementary , if their sum is equal to 900 A x Adjacent side to x Let Opposite side to x Adjacent side to 900 - x 90 0 - hy po ten us e x C B Opposite side to 900 - x 60
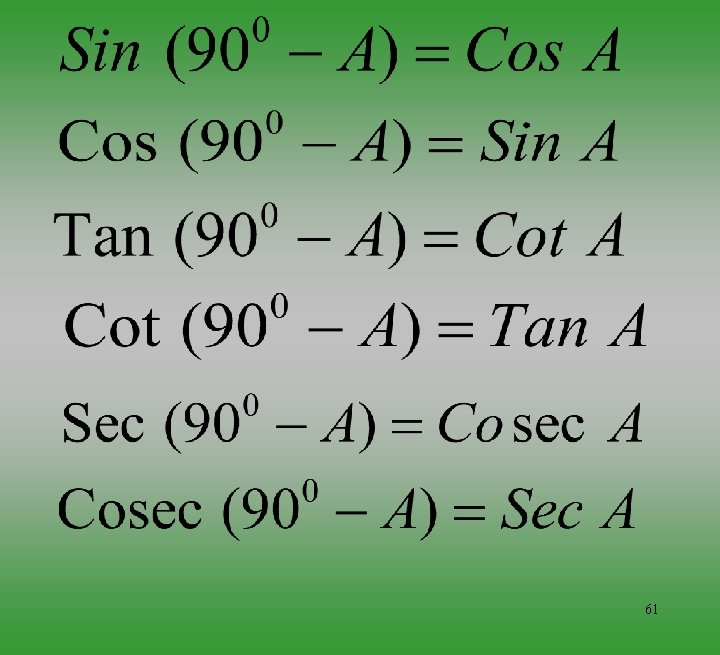
61

Example: 8 Evaluate Solution: 62

Example : 9 Where 7 A is an acute angle, Find the value of A. Solution : Given Since 7 A is an actute angle, ( 900 – 7 A ) and ( A – 60 ) are also actute 63

Example : 10 Solution : Example : 11 If Sin A = Cos B , then Prove that A + B = 900. Given that Sin A = Cos B Express Sin 810 + Tan 810 in terms of trigonometric ratioes of angle between 00 and 450 64

Example : 11 If A, B and C are interior angles of right angle triangle ABC then Show that Solution : Given A, B and C are interior angles of right triangle ABC then On taking Sin ration on both sides 65

Exercise 11. 3 1. Evaluate Solution : 66
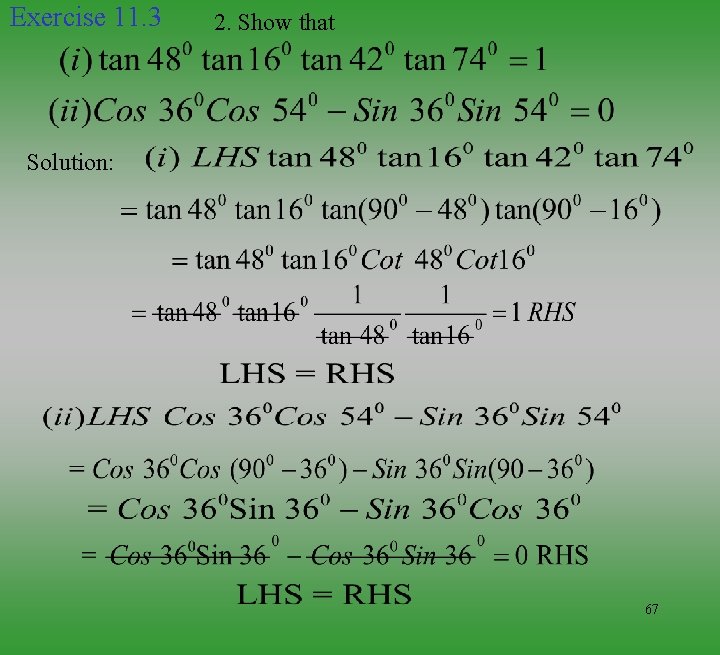
Exercise 11. 3 2. Show that Solution: 67

Exercise 11. 3 Another Method of Solution: 3. If Tan 2 A = Cot (A – 180), where 2 A is an acute anlgle. Find the value of A. Solution : Tan 2 A = Cot (A – 180) Cot ( 900 – 2 A) = Cot (A – 180) ( 900 – 2 A) = (A – 180) Cot A = Cot B AÆÿ$$¯èþ A=B 900 +180 = A + 2 A 3 A = 1080 68

Exercise 11. 3 4. If Tan A = Cot B where A and B are actute angles , Prove that A+B=900 Solution : Given that Tan A = Cot B 69

Exercise 11. 3 5. If A, B and C are interior angles of a triangle ABC, then show that Solution : Given that A, B and C are interior angles of a triangle ABC By taking tan ratio on both sides 70

Exercise 11. 3 6. Express Sin 750 + cos 650 in terms trigonometric ratioes of angles between 00 and 450 71

11. 5 Trigonometric Identities Consider a right angle triangle ABC with right angle at B. From Pythagoras theorem AC 2 + AB 2 = AC 2 C Dividing each term by AC 2 B A required trigonometric identity. 72

11. 5 Trigonometric Identities Consider a right angle triangle ABC with right angle at B. From Pythagoras theorem AC 2 + AB 2 = AC 2 C Dividing each term by AB 2 B A required trigonometric identity 73

11. 5 Trigonometric Identities Consider a right angle triangle ABC with right angle at B. From Pythagoras theorem AC 2 + AB 2 = AC 2 C Dividing each term by BC 2 B A required trigonometric identity 74
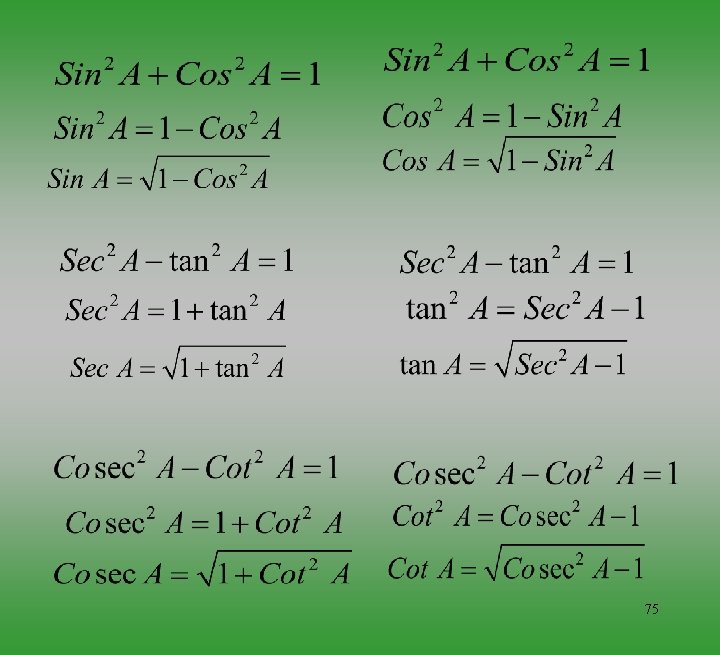
75

Do this then finc Cos A then find Sec x then find cot 76

Try This Evaluate the following and Justify your answer. 77

Example : 13 Show that Cot + tan = Sec Cosec Example : 14 Show that tan 2 + tan 4 = Sec 4 – sec 2 78

Example : 15 Show that 79

Exercise : 11. 4 1. Evaluate the following Solution: 80
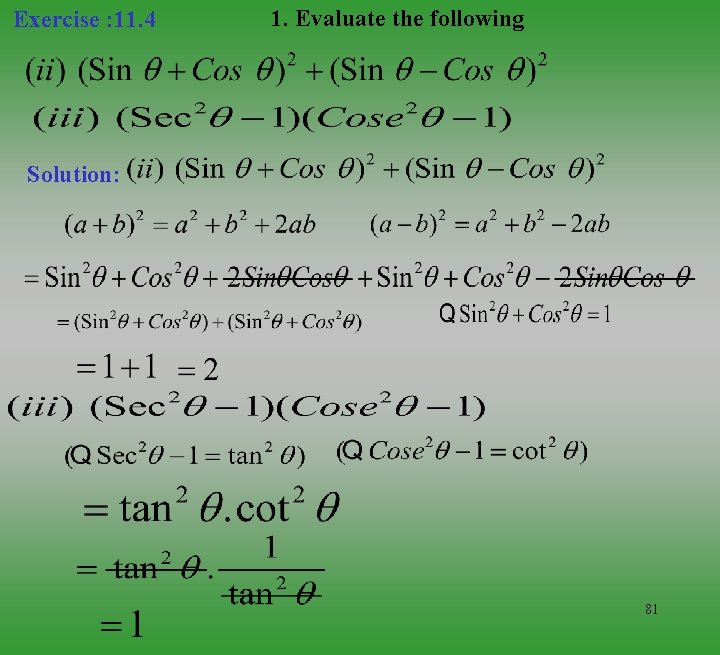
Exercise : 11. 4 1. Evaluate the following Solution: 81
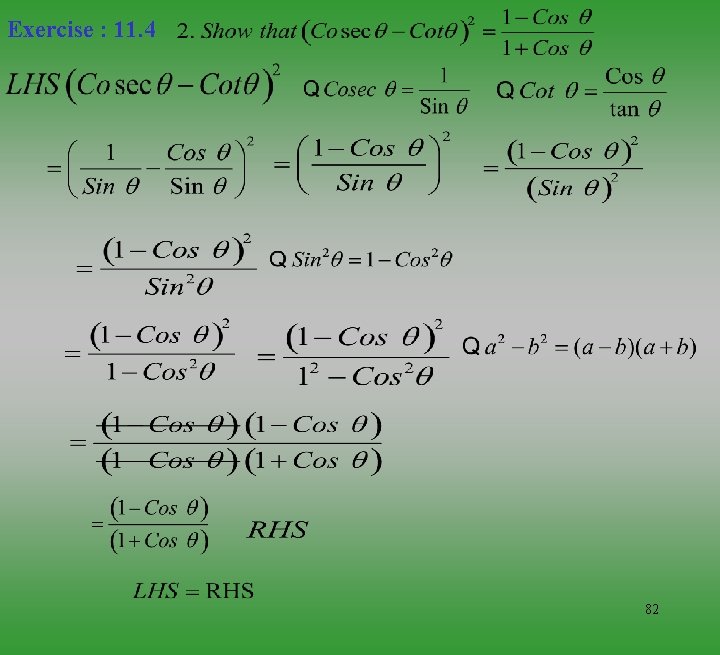
Exercise : 11. 4 82

Exercise : 11. 4 83

Exercise : 11. 4 Another Method 84

Exercise : 11. 4 85

Exercise : 11. 4 86
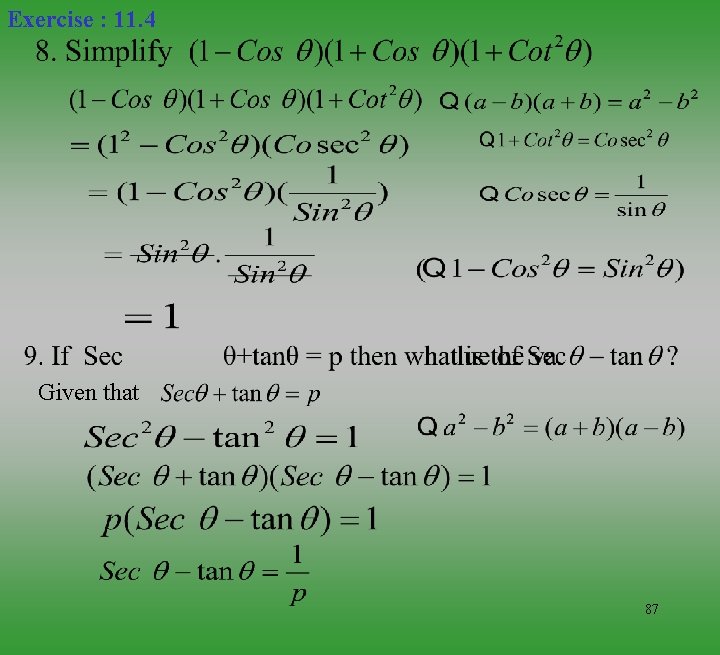
Exercise : 11. 4 Given that 87

Exercise : 11. 4 Dividing Adding by and Subtracting from 88

Exercise : 11. 4 Another method Given that 89

Optional Exercise 90

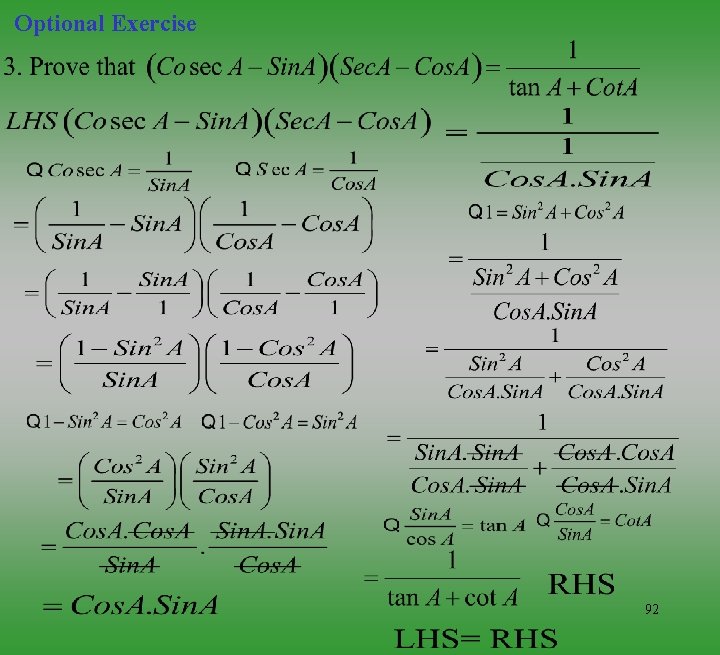
Optional Exercise Dividing Numeratior and Denominator by Cos 91

Optional Exercise 92

Optional Exercise 93

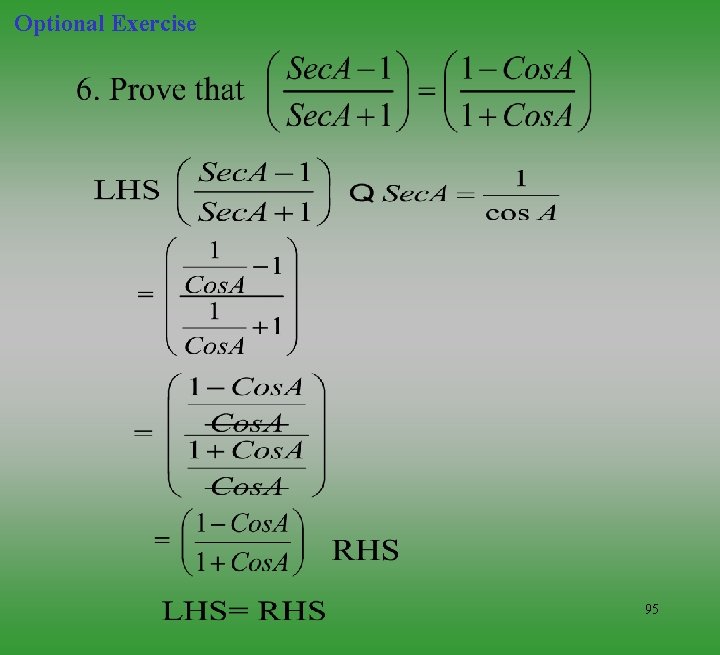
Optional Exercise 94

Optional Exercise 95
 Trigonometry is derived from greek words
Trigonometry is derived from greek words A polygon comes from two greek words poly which means
A polygon comes from two greek words poly which means Greek word photography
Greek word photography The two greek words of the word geometry are geo and metro
The two greek words of the word geometry are geo and metro Greek words used in physics
Greek words used in physics Educational technology is derived from a greek word
Educational technology is derived from a greek word What is the greek miracle in greek mythology
What is the greek miracle in greek mythology Stoicheion elements
Stoicheion elements Capital virtue
Capital virtue Greek root light
Greek root light Meter root word
Meter root word Peto root words
Peto root words Greek words for love
Greek words for love Root word anthrop
Root word anthrop Climate in greece
Climate in greece Greek or latin root/affix for cruc
Greek or latin root/affix for cruc Words with the root liter
Words with the root liter The word photography comes from the greek words
The word photography comes from the greek words The word photography comes from the greek words
The word photography comes from the greek words Words with the root crac
Words with the root crac Is latin and greek same
Is latin and greek same Greek words for death
Greek words for death Arts of economics
Arts of economics Greek root therm
Greek root therm Latin and greek roots prefixes and suffixes
Latin and greek roots prefixes and suffixes Root that means foot
Root that means foot Cyno root word
Cyno root word It comes from the 2 latin words photos and graphos
It comes from the 2 latin words photos and graphos The word photography comes from the greek words
The word photography comes from the greek words Words with dyna meaning power
Words with dyna meaning power Kinds of love
Kinds of love What are these people saying?
What are these people saying? The term audit originated from the latin word audit
The term audit originated from the latin word audit Derived adjectives examples
Derived adjectives examples Si derived unit of pressure scientist
Si derived unit of pressure scientist Satellite derived winds
Satellite derived winds What is a derived requirement
What is a derived requirement The word precis is derived from french word which means
The word precis is derived from french word which means Essentially derived variety
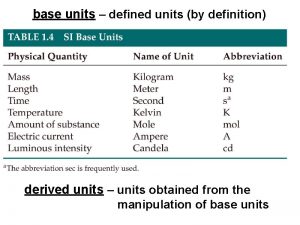
Essentially derived variety Base and derived quantities
Base and derived quantities Derived quantities
Derived quantities Derived adjectives examples
Derived adjectives examples Where does the word bank come from
Where does the word bank come from Satellite derived winds
Satellite derived winds The word report is derived from
The word report is derived from Analogous structures
Analogous structures Non separately derived system grounding diagram
Non separately derived system grounding diagram Non separately derived system grounding diagram
Non separately derived system grounding diagram Derived position definition
Derived position definition Forensic is derived from the latin word
Forensic is derived from the latin word Development of respiratory system
Development of respiratory system Structures derived from pharyngeal arches
Structures derived from pharyngeal arches What is a derived variable
What is a derived variable Kneel sitting is a derived position of
Kneel sitting is a derived position of Derived demand in shipping
Derived demand in shipping Structures derived from pharyngeal arches
Structures derived from pharyngeal arches Derived relations in sql
Derived relations in sql Physical quantities and units
Physical quantities and units Derived data structure
Derived data structure Engineering science chapter 1
Engineering science chapter 1 Derived unit definition
Derived unit definition The word authority is derived from
The word authority is derived from Alkaloids derived from tyrosine
Alkaloids derived from tyrosine Green band
Green band Attributive adjective
Attributive adjective Explain why density is a derived unit
Explain why density is a derived unit Difference between fundamental and derived unit
Difference between fundamental and derived unit Ppst domain 5 assessment and reporting
Ppst domain 5 assessment and reporting What is nc bts
What is nc bts Mosby items and derived items
Mosby items and derived items Peomus
Peomus Mosby items and derived items
Mosby items and derived items Latin word for purple
Latin word for purple Pengertian turunan fungsi aljabar
Pengertian turunan fungsi aljabar The word lens is derived from the latin word
The word lens is derived from the latin word Kamasutra standing positions
Kamasutra standing positions Meaning of
Meaning of Kalimat turunan
Kalimat turunan Briefing products of multimedia
Briefing products of multimedia Latin word literature
Latin word literature Introduction to horticulture
Introduction to horticulture Secondary immunodeficiency diseases
Secondary immunodeficiency diseases Gymnastics history
Gymnastics history Acuity charting forms
Acuity charting forms Functions of monosaccharides
Functions of monosaccharides Lliver
Lliver Mosby
Mosby Science is latin word
Science is latin word Environment derived from which word
Environment derived from which word Ejemplos de adverbios y adjetivos
Ejemplos de adverbios y adjetivos Reproductive system
Reproductive system Mosby items and derived items
Mosby items and derived items Meaning of society in education
Meaning of society in education Derived grade exams
Derived grade exams Asal kata magnet berasal dari kata
Asal kata magnet berasal dari kata Lecture is derived from
Lecture is derived from