PHYSICS QUANTITIES AND UNITS Key Word Base Quantities

PHYSICS QUANTITIES AND UNITS Key Word : Base Quantities, Derived Quantities, Scientific notation, Significant digit, Dimension, SI

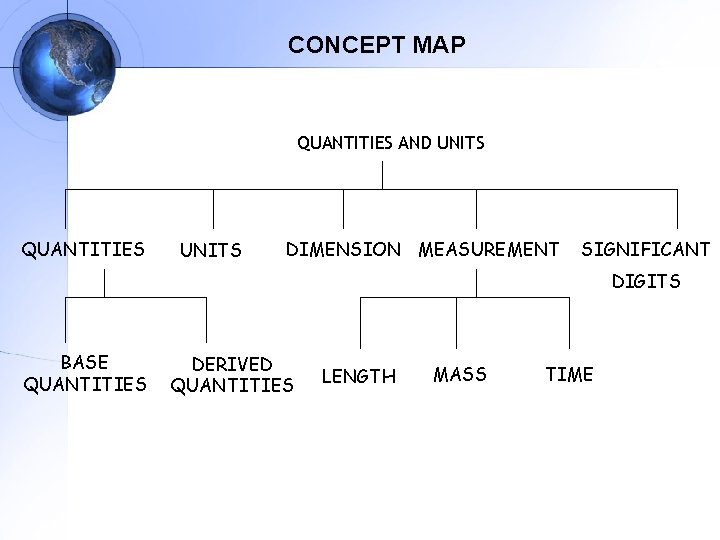
CONCEPT MAP QUANTITIES AND UNITS QUANTITIES UNITS DIMENSION MEASUREMENT SIGNIFICANT DIGITS BASE QUANTITIES DERIVED QUANTITIES LENGTH MASS TIME

objective • To analysis quantities and units in physics. • To differ between base quantities and derived quantities. • To determine SI from base quantities and derived quantities.

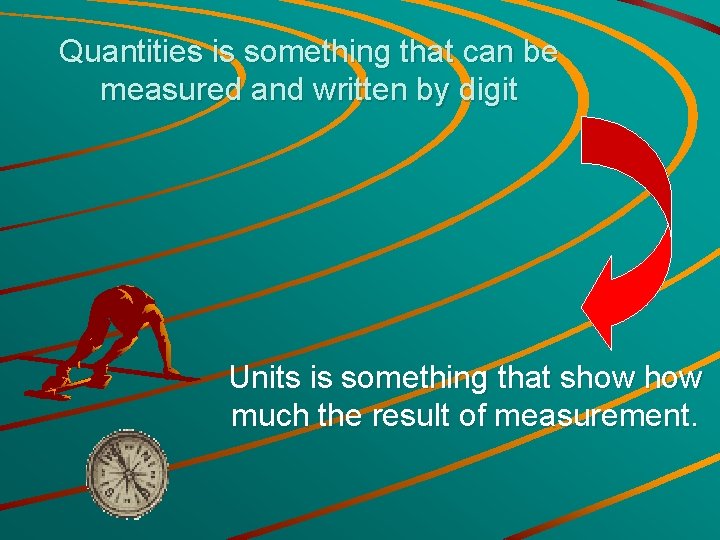
Quantities is something that can be measured and written by digit Units is something that show much the result of measurement.

Base Quantities. The unit in which these quantities are measured

Derived quantities is combination from more than one quantities Example : Velocity, acceleration, volume, force, density, work

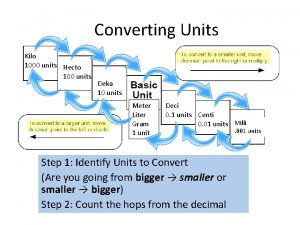
Prefixes are used to change SI units by power of 10

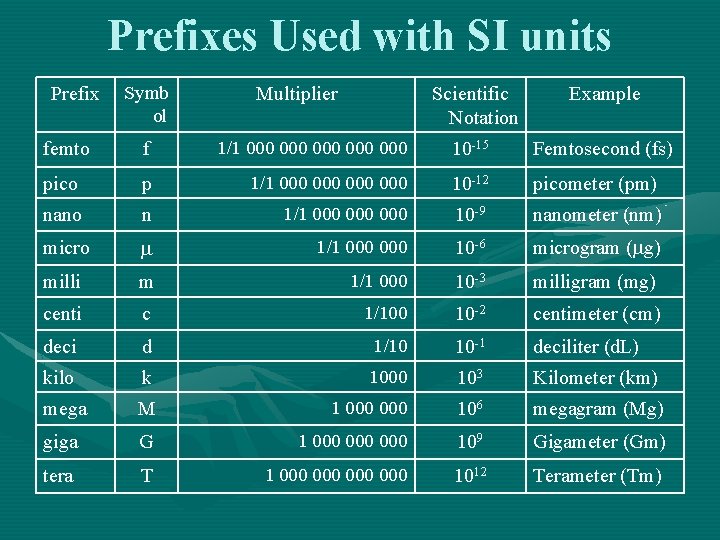
Prefixes Used with SI units Prefix Symb ol Multiplier Scientific Notation Example femto f 1/1 000 000 000 10 -15 Femtosecond (fs) pico p 1/1 000 000 10 -12 picometer (pm) nano n 1/1 000 000 10 -9 nanometer (nm) micro 1/1 000 10 -6 microgram ( g) milli m 1/1 000 10 -3 milligram (mg) centi c 1/100 10 -2 centimeter (cm) deci d 1/10 10 -1 deciliter (d. L) kilo k 1000 103 Kilometer (km) mega M 1 000 106 megagram (Mg) giga G 1 000 000 109 Gigameter (Gm) tera T 1 000 000 1012 Terameter (Tm)

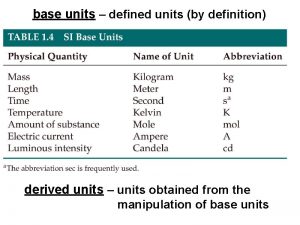
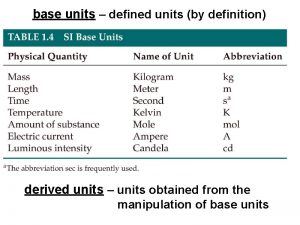
SI Base Quantities Length Mass Time Temperature Amount of Substance Electric Current Luminous Intensity Base Unit meter kilogram second Kelvin mole ampere candela Symbol m kg s K mol A cd

Derived units are combinations of the base unit Example : m/s, used to measure speed The joule, kg m 2/s 2, used to measure energy

Objectives u To define the SI standards of measurement • To use common metric prefixes. To distinguish between accuracy and prescision To indicate the precision of measured quantities with significant digit To perform arytmatic operations with significan digits • • •

Measurement is a comparison between an unknown quantities and a Standard

Scientific Notation express decimal places as power of 10 Mx n 10

Significant Digits The valid digits in a measurement are called the significant digits. The rules how to determine the number of significant digits: – – – Nonzero digits are always significant. All final zeros after the decimal point are significant Zeros used solely as placeholders are not significant The number of significant digits in measurement is an indication of the precision with which the measurement was taken.

Precision describes the degree of exactness of a measurement. Precision depends on the instrument used to make the measurement

Accuracy describes how well the results of an experiment agree with the standard value.

Expressing quantiites in scientific notation 5800 m § 5800 m = 5. 8 x 103 m 0. 000 508 kg § 0. 000 508 kg = 5. 08 10 -4 kg

Addition and subtraction using Scientific Notation 4 x 108 m + 3 x 108 m n Strategy : If the numbers have the same exponent, n, add or subtract the values of M and keep the same n n 4 x 108 m + 3 x 108 m = (4+3) x 108 m = 7 x 108 m

4. 1 x 10 -6 kg - 3. 0 x 10 -7 kg Strategy : If the exponent are not the same, move the decimal to the left or right until they are the same. Then add or subtract M 4. 1 x 10 -6 kg - 3. 0 x 10 -7 kg= 4. 1 x 10 -6 kg – 0. 30 x 10 -6 kg = (4. 1 – 0. 30) x 10 -6 kg = 3. 8 x 10 -6 kg

4. 02 x 106 m + 1. 89 x 102 m Strategy : if the magnitude of one number is quite small when compared to the other number, its effect on larger number is significant. The smaller number can be treated as zero. 4. 02 x 106 m + 1. 89 x 102 m = 40 200 x 102 m + 1. 89 x 102 m = (40 200 + 1. 89) x 102 m = 40 201. 89 x 102 m = 4. 02 x 106 m

Multipication and Division Using Scientific Notation (4 x 103 kg)(5 x 1011 m) n Strategy : multiply the values of M and add the exponents, n. Muliply the unit (4 x 103 kg)(5 x 1011 m) = (4 x 5) x 103+11 kg. m = 20 x 1014 kg. m = 2 x 1015 kg. m

Strategy : divide the values of M and substract the exponent of the divisor from the exponent of th dividend.

Determine significant digits n n 186 km has three significant digits 186 000 m has six significant digits 1. 86 x 105 m has three significant digits 1. 86000 x 105 m has six significant digits

Significant digits in additon and substraction Add 24. 686 m + 2. 343 m + 3. 21 m Ú Strategy : Note that 3. 21 m has the least number of decimal places. Round off the result to the nearest hundredth of meter. Ú Calculations: 24. 686 m 2. 343 m + 3. 21 m 30. 239 m The correct answer is 30. 24 m

Significant digits in multiplication and division Multiply 3. 22 cm by 2. 1 cm. n Strategy : The factor 2. 1 cm, contains two significant digits. State the product in two significant digits. n Calculations: 3. 22 m x 2. 1 m 6. 762 m n The correct answer is 6. 8 cm 2

Divide 36. 5 m by 3. 414 s n Strategy : The less precise factor contains three significant digits. State the answer in three significant digits. n Calculations: n The correct answer is 10. 7 m/s