Relations of Angular Linear Quantities From Ch 5



















- Slides: 20


Relations of Angular & Linear Quantities From Ch. 5 (circular motion): A mass moving in a circle has a linear velocity v & a linear acceleration a. We’ve just seen that it also has an angular velocity & an angular acceleration. There MUST be relationships between the linear & the angular quantities!

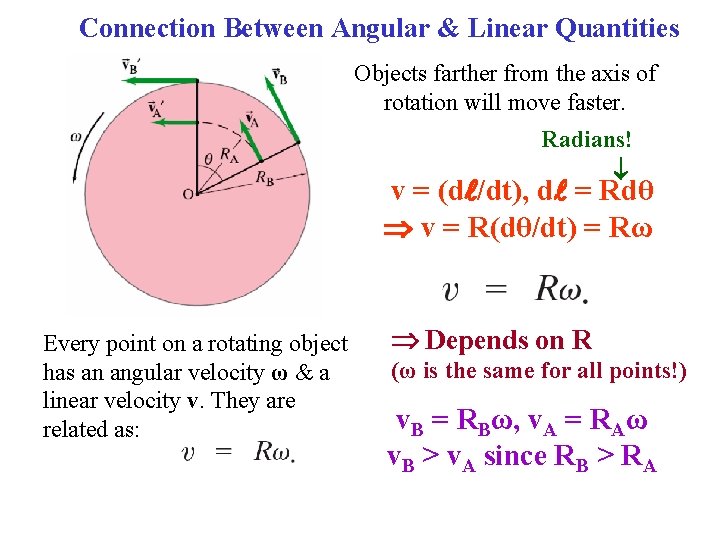
Connection Between Angular & Linear Quantities Objects farther from the axis of rotation will move faster. Radians! v = (d /dt), d = Rdθ v = R(dθ/dt) = Rω Every point on a rotating object has an angular velocity ω & a linear velocity v. They are related as: Depends on R (ω is the same for all points!) v. B = RBω, v. A = RAω v. B > v. A since RB > RA

Relations Between Angular & Linear Velocity v = (d /dt), d = Rdθ v = R(dθ/dt) = Rω v depends on R ω is the same for all points v. B = RBω v. A = RAω v. B > v. A

Conceptual Example 10 -2 Is the lion faster than the horse? On a rotating carousel or merry-go-round, one child sits on a horse near the outer edge & another child sits on a lion halfway out from the center. a. Which child has the greater linear velocity v? b. Which child has the greater angular velocity ω?

Relation Between Angular & Linear Acceleration If the angular velocity ω of a rotating object changes, it has a tangential acceleration (in the direction of the motion). dv = Rdω atan = rα atan depends on r α is the same for all points

Angular & Linear Acceleration Even if the angular velocity ω is constant, each point on the object has a radial or centripetal acceleration. From Ch. 5 discussion, this is to the motion direction. a. R depends on r ω is the same for all points in the object

Total Acceleration Two VECTOR components of acceleration • Tangential: atan= rα • Radial: a. R= rω2 • Total acceleration = Vector Sum: a = a. R+ atan a ---

Angular Velocity & Rotation Frequency Rotation frequency: f = # revolutions/second (rev/s) 1 rev = 2π rad ω = 2π f = Angular Frequency 1 rev/s 1 Hz (Hertz) Period: Time for one revolution. = (2π/ω)

Translational-Rotational Analogues & Connections ANALOGUES Translation Rotation Displacement x θ Velocity v ω Acceleration a α CONNECTIONS d = rθ, v = rω atan= r α a. R = (v 2/r) = ω2 r

Correspondence between Linear & Rotational quantities

Example 10 -3: Angular & Linear Velocities & Accelerations A carousel is initially at rest (ω0 = 0). At t = 0 it is given a constant angular acceleration α = 0. 06 rad/s 2. At t = 8 s, calculate the following: a. The angular velocity ω of the carousel. b. The linear velocity v of a child located r = 2. 5 m from the center. c. The tangential (linear) acceleration atan of that child. d. The centripetal acceleration a. R of the child. e. The total linear acceleration a of the child.

Example 10 -4: Hard Drive The platter of the hard drive of a computer rotates at frequency f = 7200 rpm (rpm = revolutions per minute = rev/min) a. Calculate the angular velocity ω (rad/s) of the platter. b. The reading head of the drive r = 3 cm (= 0. 03 m) from the rotation axis. Calculate the linear speed v of the point on the platter just below it. c. If a single bit requires 0. 5 μm of length along the direction of motion, how many bits per second can the writing head write when it is r = 3 cm from the axis?

Example 10 -5: Given ω as function of time A disk of radius R = 3 m rotates at an angular velocity ω = (1. 6 + 1. 2 t) rad/s where t is in seconds. At t = 2 s, calculate: a. The angular acceleration. b. The speed v & the components atan & a. R of the acceleration a of a point on the edge of the disk.

Section 10 -2: Vector Nature of Angular Quantities The angular velocity vector points along the axis of rotation, with the direction given by the righthand rule. If the direction of the rotation axis does not change, the angular acceleration vector points along it as well.

Sect. 10. 3: Kinematic Equations • Recall: 1 dimensional kinematic equations for uniform (constant) acceleration (Ch. 2). • We’ve just seen analogies between linear & angular quantities: Displacement & Angular Displacement: x θ Velocity & Angular Velocity: v ω Acceleration & Angular Acceleration: a α • For α = constant, we can use the same kinematic equations from Ch. 2 with these replacements!

The equations of motion for constant angular acceleration are the same as those for linear motion, with the substitution of the angular quantities for the linear ones.

Example 10 -6: Centrifuge Acceleration A centrifuge rotor is accelerated from rest to frequency f = 20, 000 rpm in 30 s. a. Calculate its average angular acceleration. b. Through how many revolutions has the centrifuge rotor turned during its acceleration period, assuming constant angular acceleration?

Example: Rotating Wheel • A wheel rotates with constant angular acceleration α = 3. 5 rad/s 2. It’s angular speed at time t = 0 is ω0 = 2. 0 rad/s. (A) Calculate the angular displacement Δθ it makes after t = 2 s. Use: Δθ = ω0 t + (½)αt 2 = (2)(2) + (½)(3)(2)2 = 11. 0 rad (630º) (B) Calculate the number of revolutions it makes in this time. Convert Δθ from radians to revolutions: A full circle = 360º = 2π radians = 1 revolution 11. 0 rad = 630º = 1. 75 rev (C) Find the angular speed ω after t = 2 s. Use: ω = ω0 + αt = 2 + (3. 5)(2) = 9 rad/s

Example: CD Player • Consider a CD player playing a CD. For the player to read a CD, the angular speed ω must vary to keep the (v = ωr). A CD has inner radius ri = 23 mm = 2. 3 10 -2 m & outer radius ro = 58 mm = 5. 8 10 -2 m. The tangential speed at the outer radius is v = 1. 3 m/s. (A) Find angular speed in rev/min at the inner & outer radii: ωi = (v/ri) = (1. 3)/(2. 3 10 -2) = 57 rad/s = 5. 4 102 rev/min ωo = (v/ro) = (1. 3)/(5. 8 10 -2) = 22 rad/s = 2. 1 102 rev/min tangential speed constant • (B) Standard playing time for a CD is 74 min, 33 s (= 4, 473 s). How many revolutions does the disk make in that time? θ = (½)(ωi + ωf)t = (½)(57 + 22)(4, 473 s) = 1. 8 105 radians = 2. 8 104 revolutions
 Angular acceleration and linear acceleration
Angular acceleration and linear acceleration Kinematics equations
Kinematics equations Angular vs linear momentum
Angular vs linear momentum Theorem of angular momentum
Theorem of angular momentum Employee relations in public relations
Employee relations in public relations Linear and angular kinematics
Linear and angular kinematics Vmax=aw
Vmax=aw Angular acceleration and linear acceleration
Angular acceleration and linear acceleration Conservation of linear momentum
Conservation of linear momentum Moment of inertia for a hoop
Moment of inertia for a hoop Velocidade linear formula
Velocidade linear formula Aceleração angular para linear
Aceleração angular para linear Movimentos circulares
Movimentos circulares Characteristics of relations and functions
Characteristics of relations and functions 2-2 practice linearity and symmetry answers
2-2 practice linearity and symmetry answers Linear relations and functions
Linear relations and functions Solving linear homogeneous recurrence relations
Solving linear homogeneous recurrence relations How to tell if a table is linear
How to tell if a table is linear Cara penggal lereng
Cara penggal lereng Linear pipeline processors
Linear pipeline processors Simultaneous equations linear and non linear
Simultaneous equations linear and non linear