Rotational Kinematics and Energy Rotational Motion Up until












































































- Slides: 101

Rotational Kinematics and Energy

Rotational Motion Up until now we have been looking at the kinematics and dynamics of translational motion – that is, motion without rotation. Now we will widen our view of the natural world to include objects that both rotate and translate. We will develop descriptions (equations) that describe rotational motion Now we can look at motion of bicycle wheels, roundabouts and divers.

I. Rotational variables - Angular position, displacement, velocity, acceleration II. Rotation with constant angular acceleration III. Relation between linear and angular variables - Position, speed, acceleration IV. Kinetic energy of rotation V. Rotational inertia VI. Torque VII. Newton’s second law for rotation VIII. Work and rotational kinetic energy

Rotational kinematics • In the kinematics of rotation we encounter new kinematic quantities – Angular displacement q – Angular speed w – Angular acceleration a – Rotational Inertia I – Torque t • All these quantities are defined relative to an axis of rotation

Angular displacement • Measured in radians or degrees • There is no dimension Dq = qf - qi qi Dq Axis of rotation qf

Angular displacement and arc length • Arc length depends on the distance it is measured away from the axis of rotation r P qi Q sp sq Axis of rotation qf

Angular Speed • Angular speed is the rate of change of angular position • We can also define the instantaneous angular speed

Average angular velocity and tangential speed • Recall that speed is distance divided by time elapsed • Tangential speed is arc length divided by time elapsed • And because we can write

Average Angular Acceleration • Rate of change of angular velocity • Instantaneous angular acceleration

Angular acceleration and tangential acceleration • We can find a link between tangential acceleration at and angular acceleration α • So

Centripetal acceleration • We have that • But we also know that • So we can also say

Example: Rotation • A dryer rotates at 120 rpm. What distance do your clothes travel during one half hour of drying time in a 70 cm diameter dryer? What angle is swept out?

Example: Rotation • A dryer rotates at 120 rpm. What distance do your clothes travel during one half hour of drying time in a 70 cm diameter dryer? What angle is swept out? • Angle: Dq = w Dt = 120 r/min x 0. 5 x 60 min = 120 x 2 p (rad) /min x 60 min/h x 0. 5 h = 2. 3 x 104 r – Distance: s = Dq r and w = Dq/Dt so s = w. Dtr – s = 120 x 2 p(rad)/min x 60 min/h x 0. 5 h x 0. 35 m = 1. 3 km

Rotational motion with constant angular acceleration • We will consider cases where a is constant • Definitions of rotational and translational quantities look similar • The kinematic equations describing rotational motion also look similar • Each of the translational kinematic equations has a rotational analogue

Rotational and Translational Kinematic Equations

Constant a motion What is the angular acceleration of a car’s wheels (radius 25 cm) when a car accelerates from 2 m/s to 5 m/s in 8 seconds?

Constant a motion What is the angular acceleration of a car’s wheels (radius 25 cm) when a car accelerates from 2 m/s to 5 m/s in 8 seconds?

A rotating wheel requires 3. 00 s to rotate through 37. 0 revolutions. Its angular speed at the end of the 3. 00 -s interval is 98. 0 rad/s. What is the constant angular acceleration of the wheel?

A rotating wheel requires 3. 00 s to rotate through 37. 0 revolutions. Its angular speed at the end of the 3. 00 -s interval is 98. 0 rad/s. What is the constant angular acceleration of the wheel?

Example: Centripetal Acceleration • A 1000 kg car goes around a bend that has a radius of 100 m, travelling at 50 km/h. What is the centripetal force? What keeps the car on the bend? [What keeps the skater in the arc? ]

Example: Centripetal Acceleration • A 1000 kg car goes around a bend that has a radius of 100 m, travelling at 50 km/h. What is the centripetal force? What keeps the car on the bend? [What keeps the skater in the arc? ] Friction keeps the car and skater on the bend

Car rounding a bend Frictional force of road on tires supplies centripetal force If ms between road and tires is lowered then frictional force may not be enough to provide centripetal force…car will skid Locking wheels makes things worse as mk < ms Banking of roads at corners reduces the risk of skidding…

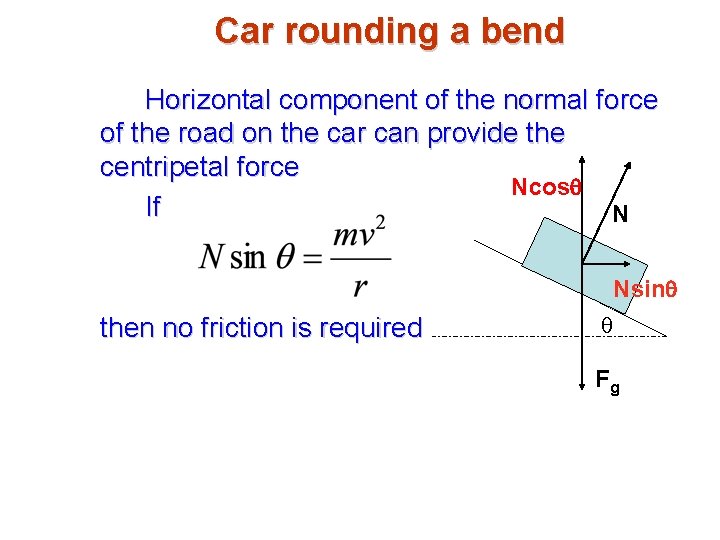
Car rounding a bend Horizontal component of the normal force of the road on the car can provide the centripetal force Ncosq If N Nsinq then no friction is required q Fg

An automobile makes a turn whose radius is 150 m. The road is banked at an angle of 18°, and the coefficient of friction between the wheels and road is 0. 3. Find the maximum speed for the car to stay on the road without skidding the banked road.

An automobile makes a turn whose radius is 150 m. The road is banked at an angle of 18°, and the coefficient of friction between the wheels and road is 0. 3. Find the maximum speed for the car to stay on the road without skidding the banked road. x-component: FN sin q + fs cos q = ma = mv 2/R; y-component: FN cos q – fs sin q – mg = 0. FN cos q – ms. FN sin q = mg, FN = mg/(cos q – ms sin q).

An automobile makes a turn whose radius is 150 m. The road is banked at an angle of 18°, and the coefficient of friction between the wheels and road is 0. 3. Find the maximum speed for the car to stay on the road without skidding the banked road. From the x-equation we get:

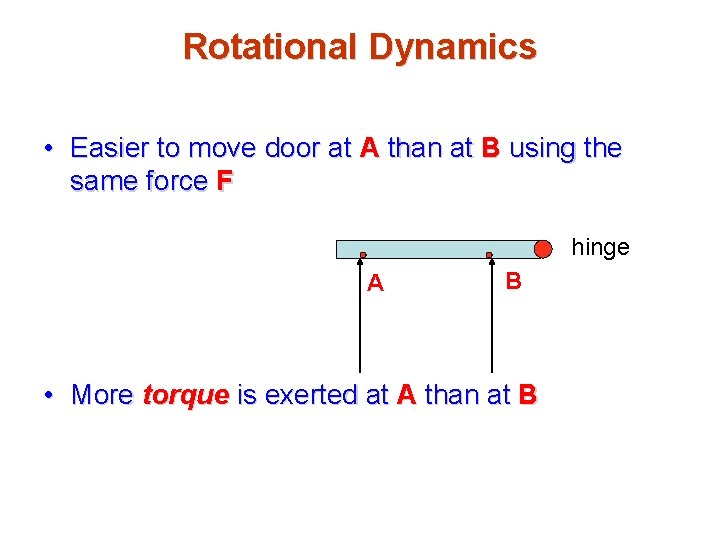
Rotational Dynamics • Easier to move door at A than at B using the same force F hinge A B • More torque is exerted at A than at B

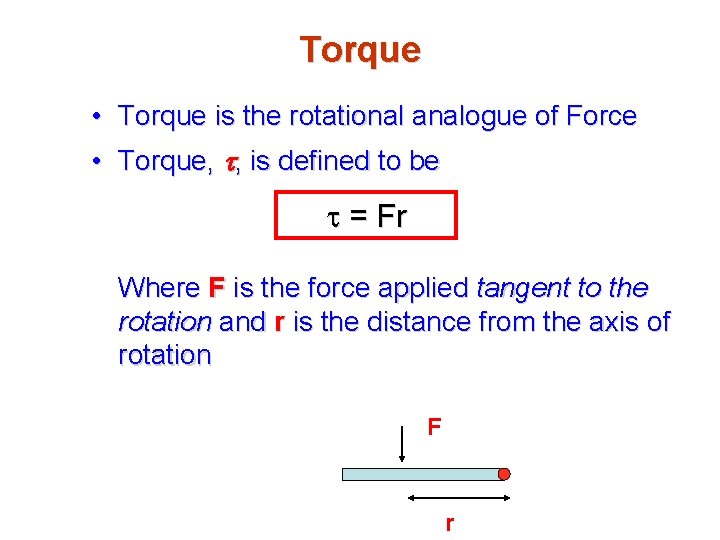
Torque • Torque is the rotational analogue of Force • Torque, t, is defined to be t = Fr Where F is the force applied tangent to the rotation and r is the distance from the axis of rotation F r

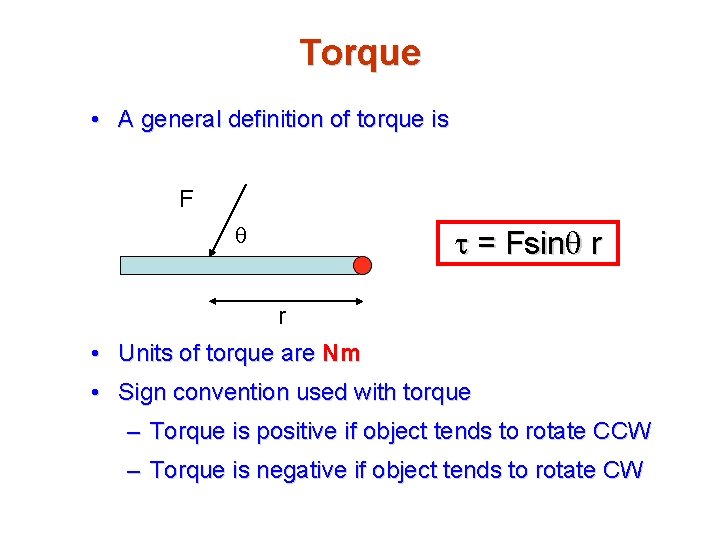
Torque • A general definition of torque is F q t = Fsinq r r • Units of torque are Nm • Sign convention used with torque – Torque is positive if object tends to rotate CCW – Torque is negative if object tends to rotate CW

Condition for Equilibrium • We know that if an object is in (translational) equilibrium then it does not accelerate. We can say that SF = 0 • An object in rotational equilibrium does not change its rotational speed. In this case we can say that there is no net torque or in other words that: St = 0

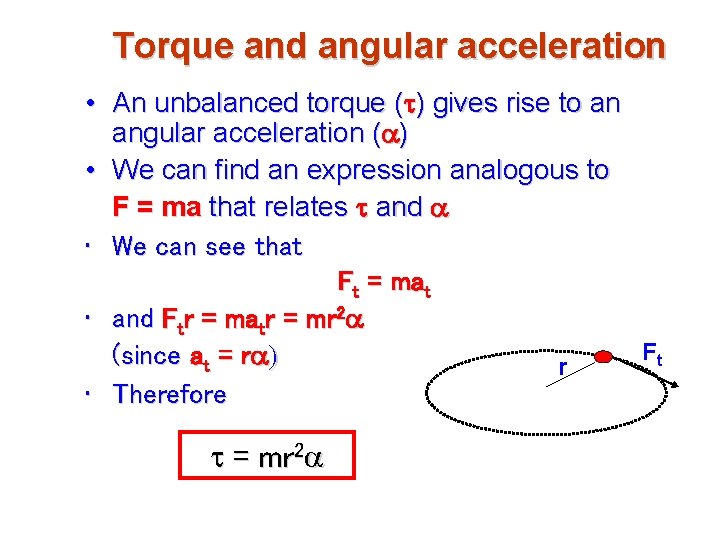
Torque and angular acceleration • An unbalanced torque (t) gives rise to an angular acceleration (a) • We can find an expression analogous to F = ma that relates t and a • We can see that Ft = mat • and Ftr = matr = mr 2 a Ft m (since at = ra) r • Therefore t = mr 2 a

Torque and Angular Acceleration t = mr 2 a Angular acceleration is directly proportional to the net torque, but the constant of proportionality has to do with both the mass of the object and the distance of the object from the axis of rotation – in this case the constant is mr 2 This constant is called the moment of inertia. Its symbol is I, and its units are kgm 2 I depends on the arrangement of the rotating system. It might be different when the same mass is rotating about a different axis

Newton’s Second Law for Rotation • We now have that t = Ia • Where I is a constant related to the distribution of mass in the rotating system • This is a new version of Newton’s second law that applies to rotation

A fish takes a line and pulls it with a tension of 15 N for 20 seconds. The spool has a radius of 7. 5 cm. If the moment of inertia of the reel is 10 kgm 2, through how many rotations does the reel spin? (Assume there is no friction)

A fish takes a line and pulls it with a tension of 15 N for 20 seconds. The spool has a radius of 7. 5 cm. If the moment of inertia of the reel is 10 kgm 2, through how many rotations does the reel spin? (Assume there is no friction) The torque and corresponding angular acceleration are Using rotational kinematics, the angle through which the spool spins is If we assume the spool starts from rest (ωi= 0) then which is 3. 5 rotations (divide 22. 5 by 2π rotation)

Angular Acceleration and I The angular acceleration reached by a rotating object depends on M, r, (their distribution) and T T When objects are rolling under the influence of gravity, only the mass distribution and the radius are important

Moments of Inertia for Rotating Objects I for a small mass m rotating about a point a distance r away is mr 2 What is the moment of inertia for an object that is rotating –such as a rolling object? Disc? Sphere? Hoop? Cylinder?

Moments of Inertia for Rotating Objects The total torque on a rotating system is the sum of the torques acting on all particles of the system about the axis of rotation – and since a is the same for all particles: I Smr 2 = m 1 r 12+ m 2 r 22+ m 3 r 32+… Axis of rotation

Continuous Objects To calculate the moment of inertia for continuous objects, we imagine the object to consist of a continuum of very small mass elements dm. Thus the finite sum Σmi r 2 i becomes the integral

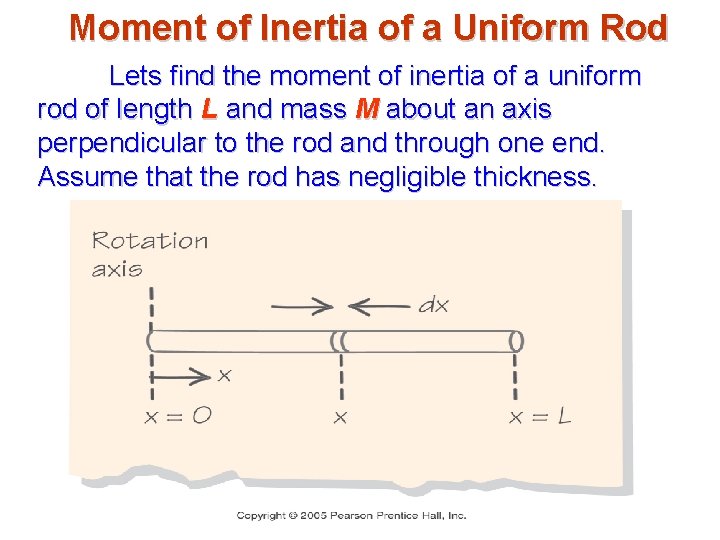
Moment of Inertia of a Uniform Rod Lets find the moment of inertia of a uniform rod of length L and mass M about an axis perpendicular to the rod and through one end. Assume that the rod has negligible thickness. L

Moment of Inertia of a Uniform Rod We choose a mass element dm at a distance x from the axes. The mass per unit length (linear mass density) is λ = M / L

Moment of Inertia of a Uniform Rod dm = λ dx

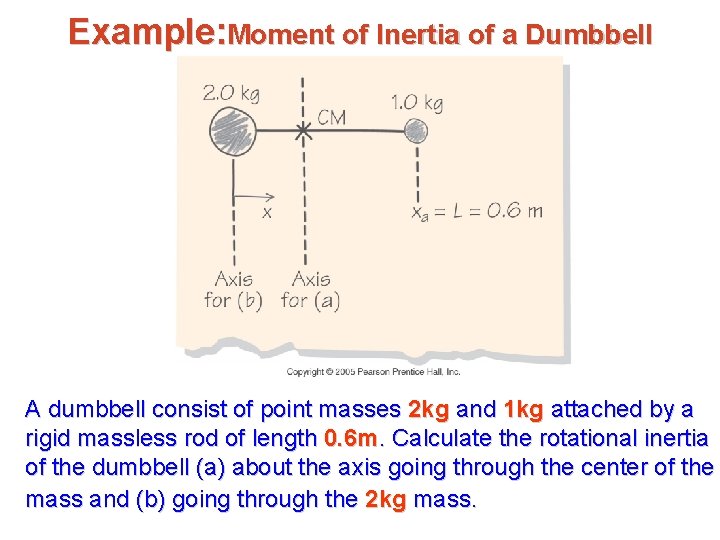
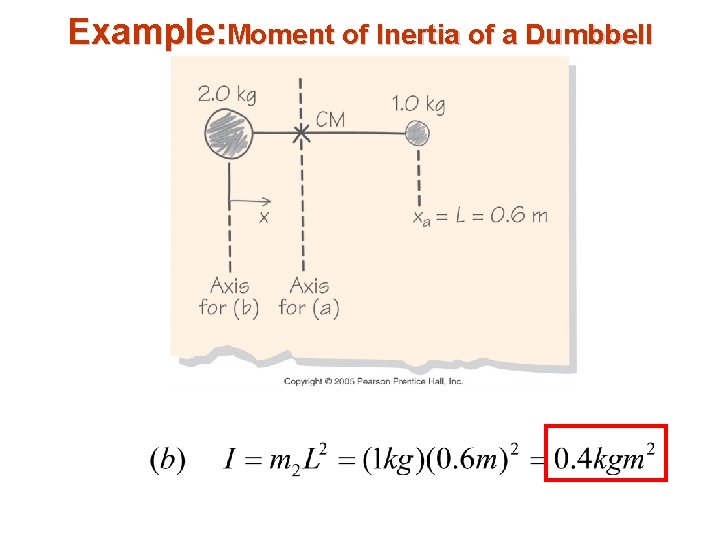
Example: Moment of Inertia of a Dumbbell A dumbbell consist of point masses 2 kg and 1 kg attached by a rigid massless rod of length 0. 6 m. Calculate the rotational inertia of the dumbbell (a) about the axis going through the center of the mass and (b) going through the 2 kg mass.

Example: Moment of Inertia of a Dumbbell

Example: Moment of Inertia of a Dumbbell

Moment of Inertia of a Uniform Hoop dm All mass of the hoop M is at distance r = R from the axis R

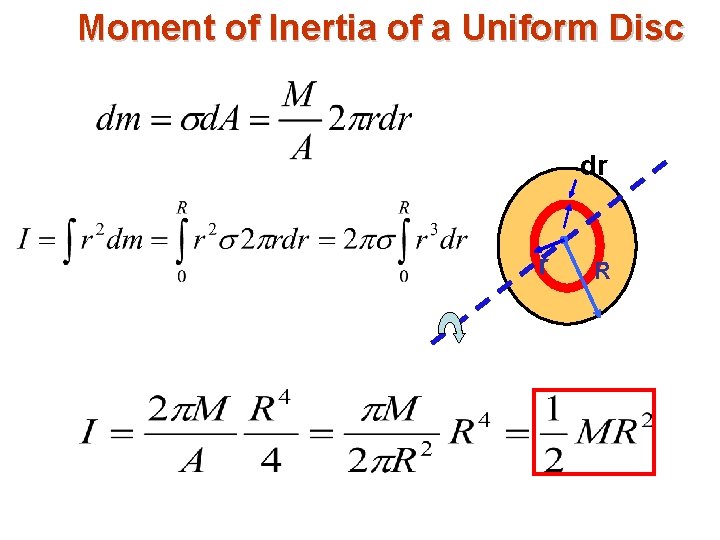
Moment of Inertia of a Uniform Disc We expect that I will be smaller than MR 2 since the mass is uniformly distributed from r = 0 to r = R rather than being concentrated at r = R as it is in the hoop. dr r R Each mass element is a hoop of radius r and thickness dr. Mass per unit area σ = M / A = M /πR 2

Moment of Inertia of a Uniform Disc dr r R

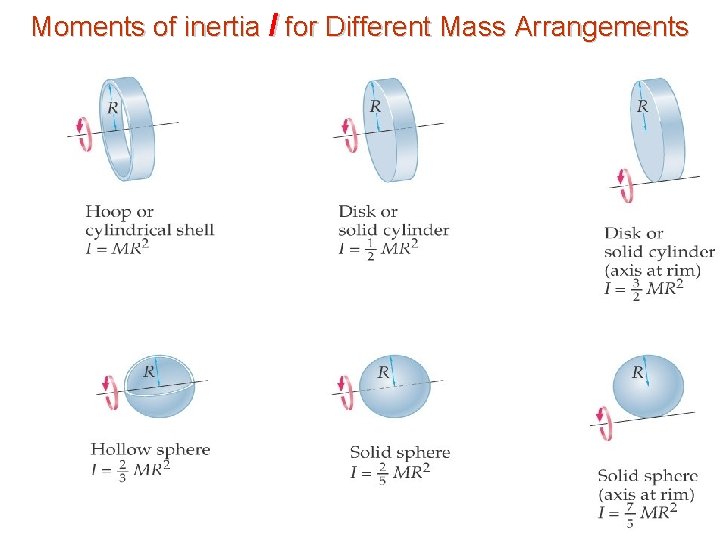
Moments of inertia I for Different Mass Arrangements

Moments of inertia I for Different Mass Arrangements

Which one will win? A hoop, disc and sphere all rolled down an inclined plane. Which one will win?

Which one will win? A hoop, disc and sphere all rolled down an inclined plane. Which one will win? 1. Hoop I = MR 2 2. Disc I = ½MR 2 3. Sphere I = 2/5 MR 2 a =t/I 1. a 1 = t / MR 2 2. α 2= 2(t / MR 2) 3. a 3 = 2. 5(t / MR 2)

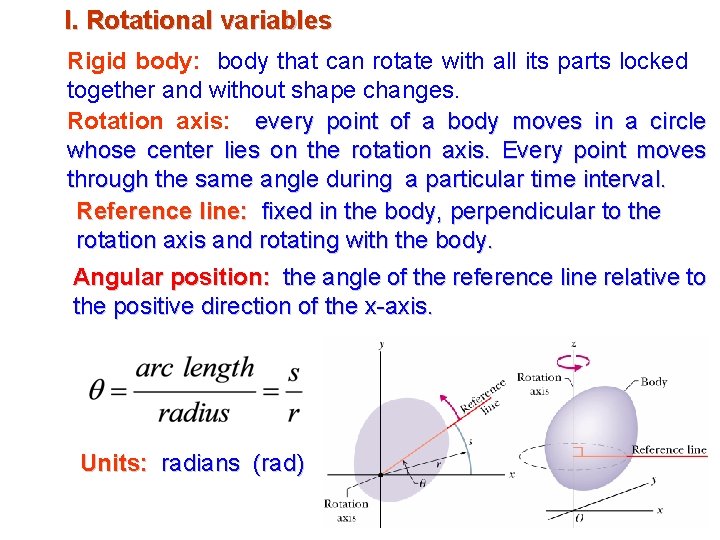
I. Rotational variables Rigid body: body that can rotate with all its parts locked together and without shape changes. Rotation axis: every point of a body moves in a circle whose center lies on the rotation axis. Every point moves through the same angle during a particular time interval. Reference line: fixed in the body, perpendicular to the rotation axis and rotating with the body. Angular position: the angle of the reference line relative to the positive direction of the x-axis. Units: radians (rad)

Note: we do not reset θ to zero with each complete rotation of the reference line about the rotation axis. 2 turns θ =4π Translation: body’s movement described by x(t). Rotation: body’s movement given by θ(t) = angular position of the body’s reference line as function of time. Angular displacement: body’s rotation about its axis changing the angular position from θ 1 to θ 2. Clockwise rotation negative Counterclockwise rotation positive

Angular velocity: Average: Instantaneous: Units: rad/s or rev/s

These equations hold not only for the rotating rigid body as a whole but also for every particle of that body because they are all locked together. Angular speed (ω): magnitude of the angular velocity. Angular acceleration: Average: Instantaneous:

Angular quantities are “normally” vector quantities right hand rule. Examples: angular velocity, angular acceleration Exception: angular displacements Object rotates around the direction of the vector a vector defines an axis of rotation not the direction in which something is moving.

II. Rotation with constant angular acceleration Linear equations Angular equations

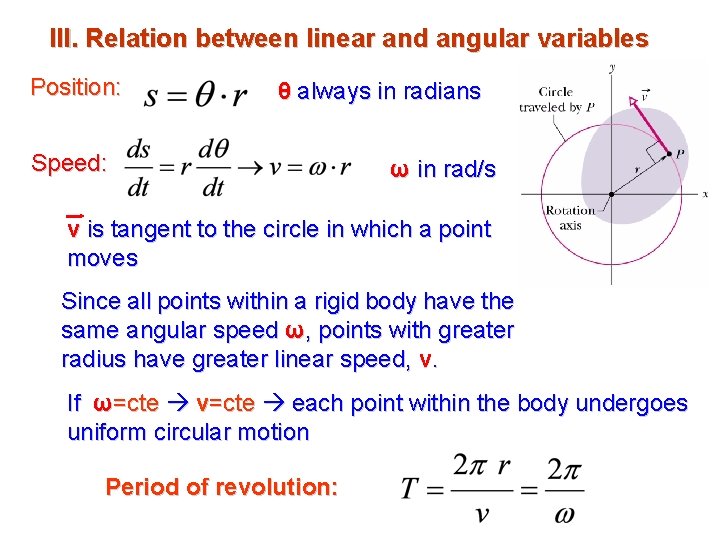
III. Relation between linear and angular variables Position: θ always in radians Speed: ω in rad/s v is tangent to the circle in which a point moves Since all points within a rigid body have the same angular speed ω, points with greater radius have greater linear speed, v. If ω=cte v=cte each point within the body undergoes uniform circular motion Period of revolution:

Acceleration: Tangential component of linear acceleration Radial component of linear acceleration: Units: m/s 2 Responsible for changes in the direction of the linear velocity vector v

Kinetic energy of rotation Reminder: Angular velocity, ω is the same for all particles within the rotating body. Linear velocity, v of a particle within the rigid body depends on the particle’s distance to the rotation axis (r). Moment of Inertia

Kinetic energy of a body in pure rotation Kinetic energy of a body in pure translation

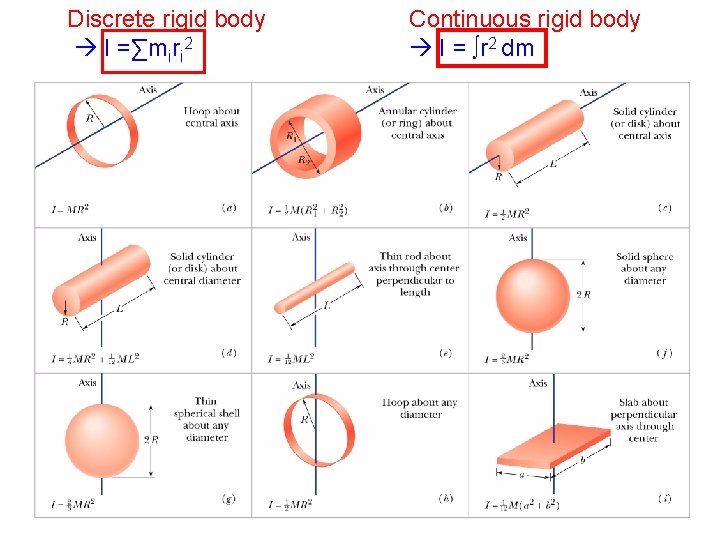
Discrete rigid body I =∑miri 2 Continuous rigid body I = ∫r 2 dm

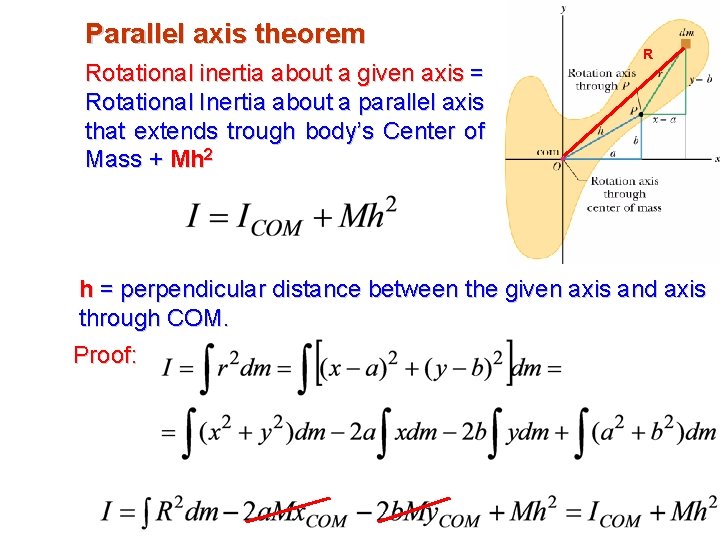
Parallel axis theorem Rotational inertia about a given axis = Rotational Inertia about a parallel axis that extends trough body’s Center of Mass + Mh 2 R h = perpendicular distance between the given axis and axis through COM. Proof:

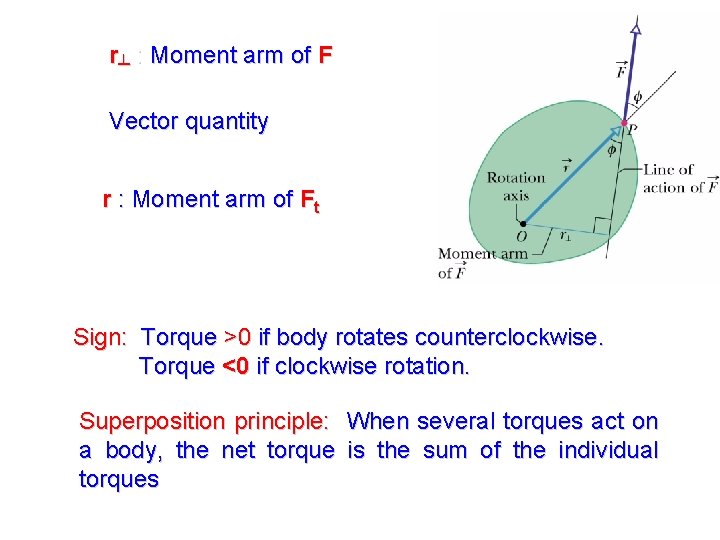
Torque: Twist “Turning action of force F ”. Units: Nm Radial component, Fr : does not cause rotation pulling a door parallel to door’s plane. Tangential component, Ft: does cause rotation pulling a door perpendicular to its plane. Ft= F sinφ

r┴ : Moment arm of F Vector quantity r : Moment arm of Ft Sign: Torque >0 if body rotates counterclockwise. Torque <0 if clockwise rotation. Superposition principle: When several torques act on a body, the net torque is the sum of the individual torques

Newton’s second law for rotation Proof: Particle can move only along the circular path only the tangential component of the force Ft (tangent to the circular path) can accelerate the particle along the path.

VII. Work and Rotational kinetic energy Translation Rot Work-kinetic energy Theorem Work, rotation about fixed axis Work, constant torque Power, rotation about fixed axis Proof:

Rotational Kinetic Energy We must rewrite our statements of conservation of mechanical energy to include KEr Must now allow that (in general): ½ mv 2+mgh+ ½ Iw 2 = constant Could also add in e. g. spring PE

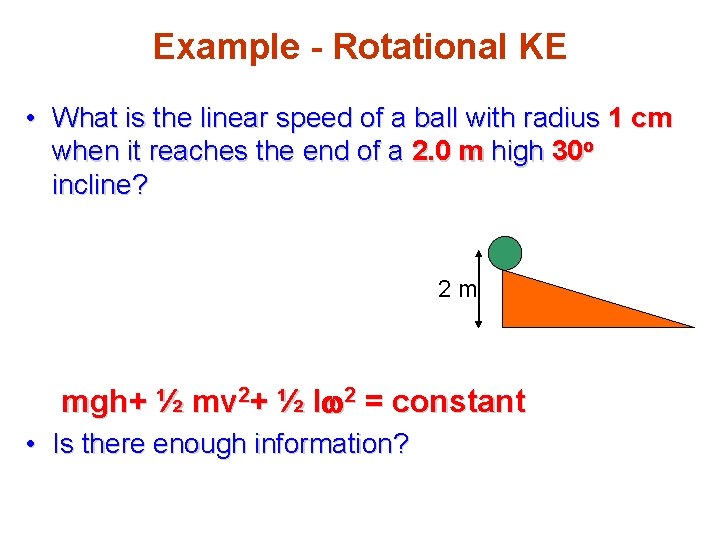
Example - Rotational KE • What is the linear speed of a ball with radius 1 cm when it reaches the end of a 2. 0 m high 30 o incline? 2 m mgh+ ½ mv 2+ ½ Iw 2 = constant • Is there enough information?

Example - Rotational KE mgh+ ½ mv 2+ ½ Iω2 = constant So we have that: The velocity of the centre of mass and the tangential speed of the sphere are the same, so we can say that: Rearranging for vf:

Example: Conservation of KEr A boy of mass 30 kg is flung off the edge of a roundabout (m = 400 kg, r = 1 m) that is travelling at 2 rpm. What is the speed of the roundabout after he falls off?

Example: Conservation of KEr A boy of mass 30 kg is flung off the edge of a roundabout (m = 400 kg, r = 1 m) that is travelling at 2 rpm. What is the speed of the roundabout after he falls off? Roundabout is a disk: Boy has

During a certain period of time, the angular position of a swinging door is described by θ= 5. 00 + 10. 0 t + 2. 00 t 2 where θ is in radians and t is in seconds. Determine the angular position, angular speed, and angular acceleration of the door (a) at t = 0 and (b) at t = 3. 00 s.

During a certain period of time, the angular position of a swinging door is described by θ= 5. 00 + 10. 0 t + 2. 00 t 2 where θ is in radians and t is in seconds. Determine the angular position, angular speed, and angular acceleration of the door (a) at t = 0 and (b) at t = 3. 00 s. Solution: (a)

During a certain period of time, the angular position of a swinging door is described by θ= 5. 00 + 10. 0 t + 2. 00 t 2 where θ is in radians and t is in seconds. Determine the angular position, angular speed, and angular acceleration of the door (a) at t = 0 and (b) at t = 3. 00 s. Solution: (b)

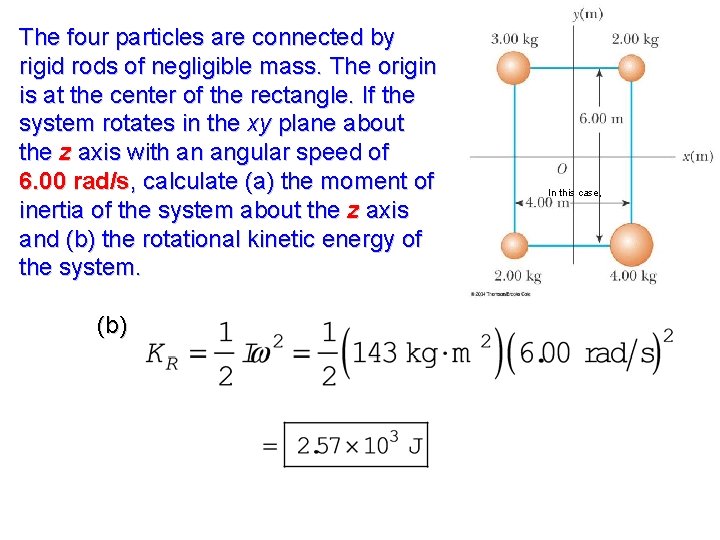
The four particles are connected by rigid rods of negligible mass. The origin is at the center of the rectangle. If the system rotates in the xy plane about the z axis with an angular speed of 6. 00 rad/s, calculate (a) the moment of inertia of the system about the z axis and (b) the rotational kinetic energy of the system.

The four particles are connected by rigid rods of negligible mass. The origin is at the center of the rectangle. If the system rotates in the xy plane about the z axis with an angular speed of 6. 00 rad/s, calculate (a) the moment of inertia of the system about the z axis and (b) the rotational kinetic energy of the system. (a)

The four particles are connected by rigid rods of negligible mass. The origin is at the center of the rectangle. If the system rotates in the xy plane about the z axis with an angular speed of 6. 00 rad/s, calculate (a) the moment of inertia of the system about the z axis and (b) the rotational kinetic energy of the system. (b) In this case,

Many machines employ cams for various purposes, such as opening and closing valves. In Figure, the cam is a circular disk rotating on a shaft that does not pass through the center of the disk. In the manufacture of the cam, a uniform solid cylinder of radius R is first machined. Then an off-center hole of radius R/2 is drilled, parallel to the axis of the cylinder, and centered at a point a distance R/2 from the center of the cylinder. The cam, of mass M, is then slipped onto the circular shaft and welded into place. What is the kinetic energy of the cam when it is rotating with angular speed ω about the axis of the shaft?

We consider the cam as the superposition of the original solid disk and a disk of negative mass cut from it. With half the radius, the cut-away part has one-quarter the face area and one-quarter the volume and one-quarter the mass of the original solid cylinder: By the parallel-axis theorem, the original cylinder had moment of inertia The negative mass portion has : The whole cam has: and

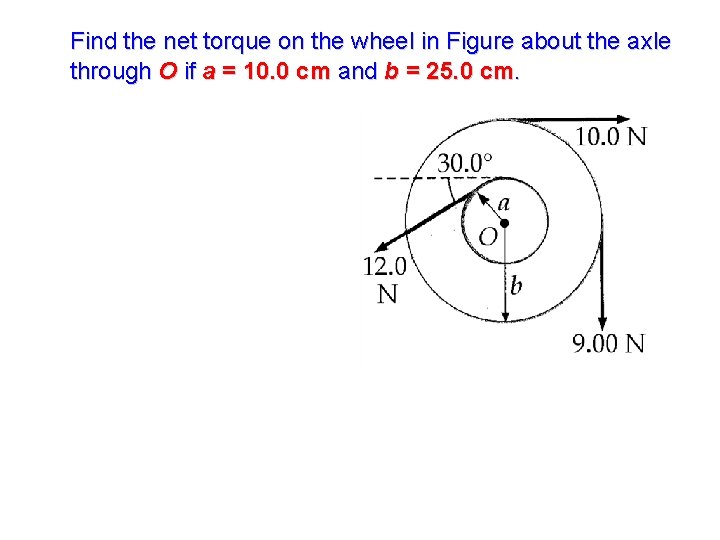
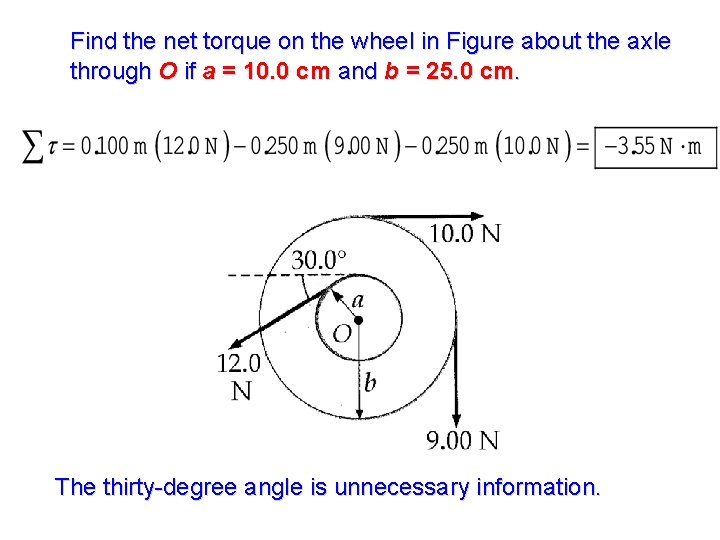
Find the net torque on the wheel in Figure about the axle through O if a = 10. 0 cm and b = 25. 0 cm.

Find the net torque on the wheel in Figure about the axle through O if a = 10. 0 cm and b = 25. 0 cm. The thirty-degree angle is unnecessary information.

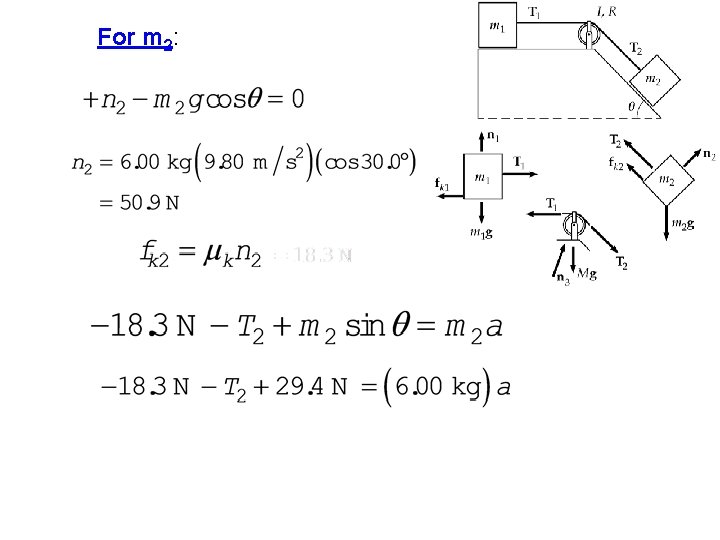
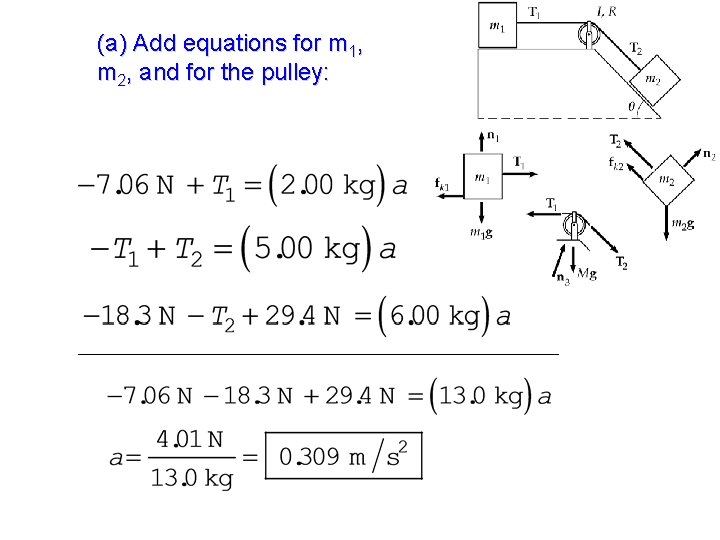
A block of mass m 1 = 2. 00 kg and a block of mass m 2 = 6. 00 kg are connected by a massless string over a pulley in the shape of a solid disk having radius R = 0. 250 m and mass M = 10. 0 kg. These blocks are allowed to move on a fixed block-wedge of angle = 30. 0 as in Figure. The coefficient of kinetic friction is 0. 360 for both blocks. Draw free-body diagrams of both blocks and of the pulley. Determine (a) the acceleration of the two blocks, and (b) the tensions in the string on both sides of the pulley.

For m 1: For pulley,

For m 2:

(a) Add equations for m 1, m 2, and for the pulley:


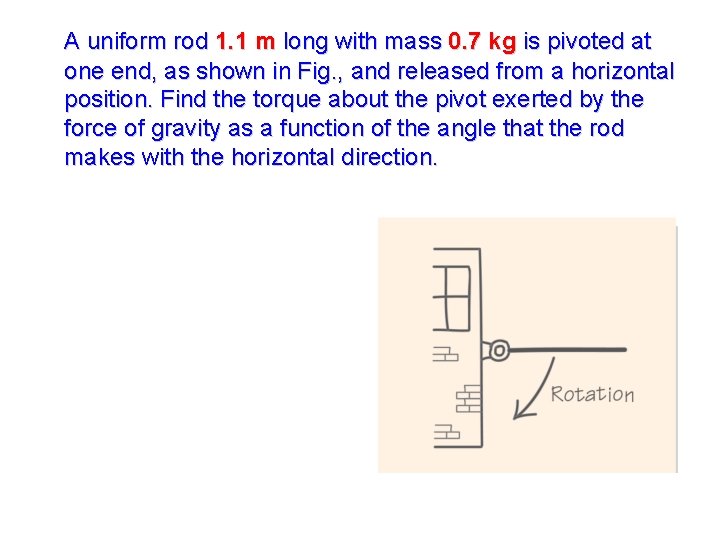
A uniform rod 1. 1 m long with mass 0. 7 kg is pivoted at one end, as shown in Fig. , and released from a horizontal position. Find the torque about the pivot exerted by the force of gravity as a function of the angle that the rod makes with the horizontal direction.

A uniform rod 1. 1 m long with mass 0. 7 kg is pivoted at one end, as shown in Fig. , and released from a horizontal position. Find the torque about the pivot exerted by the force of gravity as a function of the angle that the rod makes with the horizontal direction. From the diagram we see that the moment arm of the force of gravity is Thus θ mg

A seesaw pivots as shown in Fig. (a) What is the net torque about the pivot point? (b) Give an example for which the application of three different forces and their points of application will balance the seesaw. Two of the forces must point down and the other one up.

A seesaw pivots as shown in Fig. (a) What is the net torque about the pivot point? (b) Give an example for which the application of three different forces and their points of application will balance the seesaw. Two of the forces must point down and the other one up. (a) We choose the clockwise direction as positive. (b) We see that changing the 7 -N force to ~5. 4 N will make the torque zero. An upward force of 8. 4 N at the pivot will make the resultant force equal to zero.

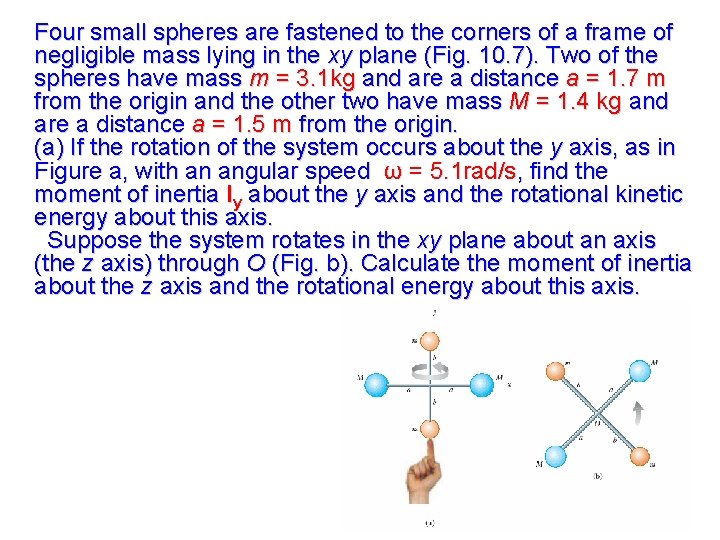
Four small spheres are fastened to the corners of a frame of negligible mass lying in the xy plane (Fig. 10. 7). Two of the spheres have mass m = 3. 1 kg and are a distance a = 1. 7 m from the origin and the other two have mass M = 1. 4 kg and are a distance a = 1. 5 m from the origin. (a) If the rotation of the system occurs about the y axis, as in Figure a, with an angular speed ω = 5. 1 rad/s, find the moment of inertia Iy about the y axis and the rotational kinetic energy about this axis. Suppose the system rotates in the xy plane about an axis (the z axis) through O (Fig. b). Calculate the moment of inertia about the z axis and the rotational energy about this axis.

Four small spheres are fastened to the corners of a frame of negligible mass lying in the xy plane (Figure). Two of the spheres have mass m = 3. 1 kg and are a distance a = 1. 7 m from the origin and the other two have mass M = 1. 4 kg and are a distance a = 1. 5 m from the origin. (a) If the rotation of the system occurs about the y axis, as in Figure a, with an angular speed ω = 5. 1 rad/s, find the moment of inertia Iy about the y axis and the rotational kinetic energy about this axis. Suppose the system rotates in the xy plane about an axis (the z axis) through O (Fig. b). Calculate the moment of inertia about the z axis and the rotational energy about this axis. (a)

Four small spheres are fastened to the corners of a frame of negligible mass lying in the xy plane (Fig. 10. 7). Two of the spheres have mass m = 3. 1 kg and are a distance a = 1. 7 m from the origin and the other two have mass M = 1. 4 kg and are a distance a = 1. 5 m from the origin. (a) If the rotation of the system occurs about the y axis, as in Figure a, with an angular speed ω = 5. 1 rad/s, find the moment of inertia Iy about the y axis and the rotational kinetic energy about this axis. Suppose the system rotates in the xy plane about an axis (the z axis) through O (Fig. b). Calculate the moment of inertia about the z axis and the rotational energy about this axis. (b)

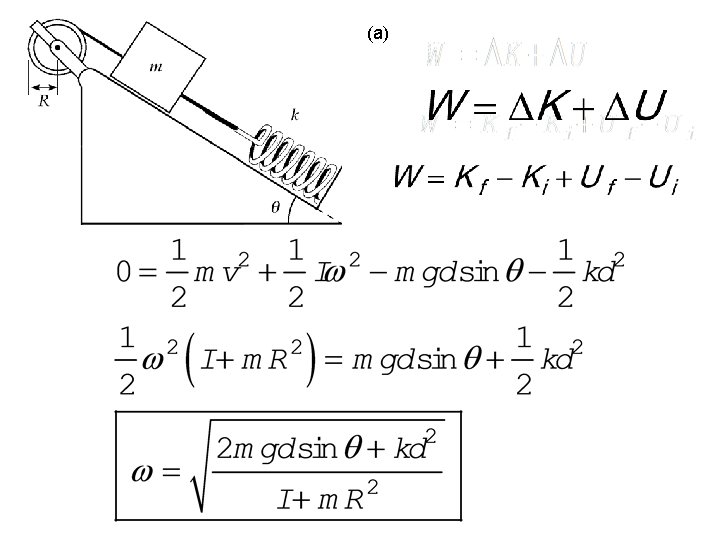
The reel shown in Figure has radius R and moment of inertia I. One end of the block of mass m is connected to a spring of force constant k, and the other end is fastened to a cord wrapped around the reel. The reel axle and the incline are frictionless. The reel is wound counterclockwise so that the spring stretches a distance d from its unstretched position and is then released from rest. (a) Find the angular speed of the reel when the spring is again unstretched. (b) Evaluate the angular speed numerically at this point if I = 1. 00 kg·m 2, R = 0. 300 m, k = 50. 0 N/m, m = 0. 500 kg, d = 0. 200 m, and θ= 37. 0°.



A tennis ball is a hollow sphere with a thin wall. It is set rolling without slipping at 4. 03 m/s on a horizontal section of a track, as shown in Figure. It rolls around the inside of a vertical circular loop 90. 0 cm in diameter, and finally leaves the track at a point 20. 0 cm below the horizontal section. (a) Find the speed of the ball at the top of the loop. Demonstrate that it will not fall from the track. (b) Find its speed as it leaves the track. (c) Suppose that static friction between ball and track were negligible, so that the ball slid instead of rolling. Would its speed then be higher, lower, or the same at the top of the loop? Explain.

A tennis ball is a hollow sphere with a thin wall. It is set rolling without slipping at 4. 03 m/s on a horizontal section of a track, as shown in Figure. It rolls around the inside of a vertical circular loop 90. 0 cm in diameter, and finally leaves the track at a point 20. 0 cm below the horizontal section. (a) Find the speed of the ball at the top of the loop. Demonstrate that it will not fall from the track. (b) Find its speed as it leaves the track. (c) Suppose that static friction between ball and track were negligible, so that the ball slid instead of rolling. Would its speed then be higher, lower, or the same at the top of the loop? Explain. (a) Energy conservation for the system of the ball and the Earth between the horizontal section and top of loop:

A tennis ball is a hollow sphere with a thin wall. It is set rolling without slipping at 4. 03 m/s on a horizontal section of a track, as shown in Figure. It rolls around the inside of a vertical circular loop 90. 0 cm in diameter, and finally leaves the track at a point 20. 0 cm below the horizontal section. (a) Find the speed of the ball at the top of the loop. Demonstrate that it will not fall from the track. (b) Find its speed as it leaves the track. (c) Suppose that static friction between ball and track were negligible, so that the ball slid instead of rolling. Would its speed then be higher, lower, or the same at the top of the loop? Explain. (a) Energy conservation for the system of the ball and the Earth between the horizontal section and top of loop:
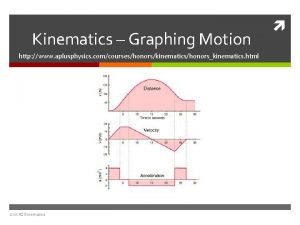
 Aplusphysics kinematics-horizontal kinematics
Aplusphysics kinematics-horizontal kinematics Rotational kinematics
Rotational kinematics Angular kinematic quantities
Angular kinematic quantities Rotational kinematics
Rotational kinematics Rotational inertia unit
Rotational inertia unit Rotational kinematics equations
Rotational kinematics equations Torque right hand rule
Torque right hand rule Rotational equilibrium and rotational dynamics
Rotational equilibrium and rotational dynamics Rectilinear kinematics
Rectilinear kinematics What is continuous motion in dynamics
What is continuous motion in dynamics What is negative velocity on a graph
What is negative velocity on a graph Galileo trick kinematics
Galileo trick kinematics Rectilinear kinematics continuous motion
Rectilinear kinematics continuous motion Kinematic equations for uniformly accelerated motion
Kinematic equations for uniformly accelerated motion Kinematics of simple harmonic motion
Kinematics of simple harmonic motion Kinematics defining motion
Kinematics defining motion Kinematics: motion along a straight line
Kinematics: motion along a straight line Motion along a straight line definition
Motion along a straight line definition Describing motion kinematics in one dimension
Describing motion kinematics in one dimension Describing motion kinematics in one dimension
Describing motion kinematics in one dimension Projectile motion equation
Projectile motion equation Uniformly accelerated motion formula
Uniformly accelerated motion formula Torque and moment of inertia
Torque and moment of inertia Angular velocity to tangential velocity
Angular velocity to tangential velocity Rotational and linear motion analogies
Rotational and linear motion analogies Physics equations quiz
Physics equations quiz Rotational vs irrotational flow
Rotational vs irrotational flow Energy energy transfer and general energy analysis
Energy energy transfer and general energy analysis Energy energy transfer and general energy analysis
Energy energy transfer and general energy analysis Ap physics rotational motion
Ap physics rotational motion Ap physics rotational motion
Ap physics rotational motion Circular motion formula
Circular motion formula The blade of a lawn mower is rotating at an angular
The blade of a lawn mower is rotating at an angular Ap physics 1 unit 7
Ap physics 1 unit 7 Translational vs rotational motion
Translational vs rotational motion Chapter 8 rotational motion study guide answer key
Chapter 8 rotational motion study guide answer key Static equilibrium rotational motion
Static equilibrium rotational motion Microwave spectroscopy
Microwave spectroscopy Rotational motion lab
Rotational motion lab Rotational motion
Rotational motion An old phonograph record revolves at 45 rpm
An old phonograph record revolves at 45 rpm Rotational motion
Rotational motion Torque rotational motion
Torque rotational motion Rigid body rotation formula
Rigid body rotation formula Moment of inertia of a dumbbell
Moment of inertia of a dumbbell Rotational motion chemistry
Rotational motion chemistry Chapter 8 rotational motion
Chapter 8 rotational motion Motion and types of motion
Motion and types of motion Moment of inertia chart
Moment of inertia chart Kinetic rotational energy formula
Kinetic rotational energy formula Rotational kinetic energy
Rotational kinetic energy Rotational kinetic energy units
Rotational kinetic energy units Rotational kinetic energy
Rotational kinetic energy Planar kinematics of a rigid body
Planar kinematics of a rigid body Kinematics
Kinematics Okc ckc
Okc ckc Kinematics and dynamics of machines
Kinematics and dynamics of machines Equation of shm
Equation of shm An object in motion stays in motion
An object in motion stays in motion Chapter 2 motion section 1 describing motion answer key
Chapter 2 motion section 1 describing motion answer key What is acceleration
What is acceleration Section 1 describing motion answer key
Section 1 describing motion answer key Chapter 1 lesson 2 describing motion answer key
Chapter 1 lesson 2 describing motion answer key Motion section 1 describing motion
Motion section 1 describing motion Chapter 9 motion and energy answer key
Chapter 9 motion and energy answer key Motion forces and energy
Motion forces and energy Energy from motion and position
Energy from motion and position Non centroidal rotation
Non centroidal rotation Energy is defined as the ability to
Energy is defined as the ability to Section 1 describing motion
Section 1 describing motion Motion and energy
Motion and energy Ppt
Ppt Sheep become lions
Sheep become lions Forms and shores must not be removed until
Forms and shores must not be removed until Rise again and again until lambs
Rise again and again until lambs Second star to the right and straight on until morning
Second star to the right and straight on until morning It's all fun and games until someone loses an i
It's all fun and games until someone loses an i A union b example
A union b example Tricycle kinematics
Tricycle kinematics What is kinematics
What is kinematics Kinematics 2d formulas
Kinematics 2d formulas Iczv
Iczv Holonomic drive
Holonomic drive Laws of kinematics
Laws of kinematics Dr frost further kinematics
Dr frost further kinematics Dynamics vs kinematics
Dynamics vs kinematics Kinematics of a particle moving in a straight line answers
Kinematics of a particle moving in a straight line answers What are the 4 kinematic equations
What are the 4 kinematic equations Instantaneous velocity formula
Instantaneous velocity formula Transport theorem kinematics
Transport theorem kinematics Closed form solutions
Closed form solutions Find jacobian matrix
Find jacobian matrix Kinematics ppt free download
Kinematics ppt free download Fluid kinematics definition
Fluid kinematics definition Kinematics ppt
Kinematics ppt Absolute acceleration
Absolute acceleration Fluid kinematics - ppt
Fluid kinematics - ppt Forward kinematics
Forward kinematics Erratic motion examples
Erratic motion examples Plane movement
Plane movement Nmt.ee
Nmt.ee Inverse kinematics
Inverse kinematics