Angular motion 1 Angular Motion o Linear Motion

Angular motion 1

Angular Motion o Linear Motion n n Location = Location + velocity Velocity = velocity + acceleration o Angular Motion n n Angle = angle + angular velocity = angular velocity + angular acceleration o Linear vel, acc are vectors and angular vel and acc are scalars o Let’s make a rotating baton 2

Let’s make a rotating baton float angle = 0; float a. Velocity = 0; float a. Acceleration = 0. 0001; void draw() { background(255); fill(127); stroke(0); void setup() { size(800, 200); smooth(); } translate(width/2, height/2); rect. Mode(CENTER); rotate(angle); stroke(0); stroke. Weight(2); fill(127); line(-60, 0, 60, 0); ellipse(60, 0, 16); ellipse(-60, 0, 16); } angle += a. Velocity; a. Velocity += a. Acceleration; 3

Exercise 1 : Let’s make a spinning box Change the wind force example • • Combining angular acc + linear acc Ball -> Box should be rotating through changing its angular acc. For just testing, let assume that angular acc = linear vel. x/20 4

Combining linear & angular acc. class Mover { void update() { velocity. add(acceleration); location. add(velocity); PVector location; PVector velocity; PVector acceleration; float mass; //This is a piece of hack!!!! -> Not correct!! a. Acceleration = acceleration. x / 20. 0; float angle = 0; float a. Velocity = 0; float a. Acceleration = 0; a. Velocity += a. Acceleration; a. Velocity = constrain(a. Velocity, -0. 1, 0. 1); angle += a. Velocity; Mover(float m, float x, float y) { mass = m; location = new PVector(x, y); velocity = new PVector(random(-1, 1), random(-1, 1)); acceleration = new PVector(0, 0); } acceleration. mult(0); void apply. Force(PVector force) { PVector f = PVector. div(force, mass); acceleration. add(f); } } void display() { stroke(0); fill(175, 200); rect. Mode(CENTER); push. Matrix(); translate(location. x, location. y); rotate(angle); rect(0, 0, mass*16); pop. Matrix(); } 5

In the old example o We control the box with mouse n n n Set the direction vector of linear acc (mouse position - ball position) Normalize Set the magnitude of acc o However, it dose not change the orientation because the ball does not have orientation o Let’s do the same example with Box (Box has orientation) 6

Pointing in the Direction of Movement o When we change the orientation of object, we need to “rotate according to the velocity vector” o First calculate the velocity, and then use the velocity. heading() to get its orientation n Note that heading() for Ver 2. 0 (old version is heading 2 D() 7

Revise the old example : Ball -> Box void display() { float theta = velocity. heading(); } stroke(0); stroke. Weight(2); fill(127); push. Matrix(); rect. Mode(CENTER); translate(location. x, location. y); rotate(theta); rect(0, 0, 30, 10); pop. Matrix(); void update() { PVector mouse = new PVector(mouse. X, mouse. Y); PVector dir = PVector. sub(mouse, location); dir. normalize(); dir. mult(0. 5); acceleration = dir; } velocity. add(acceleration); velocity. limit(topspeed); location. add(velocity); Use mouse position to change acc, and And then use vel to calculate orientation 8

Pendulum 9

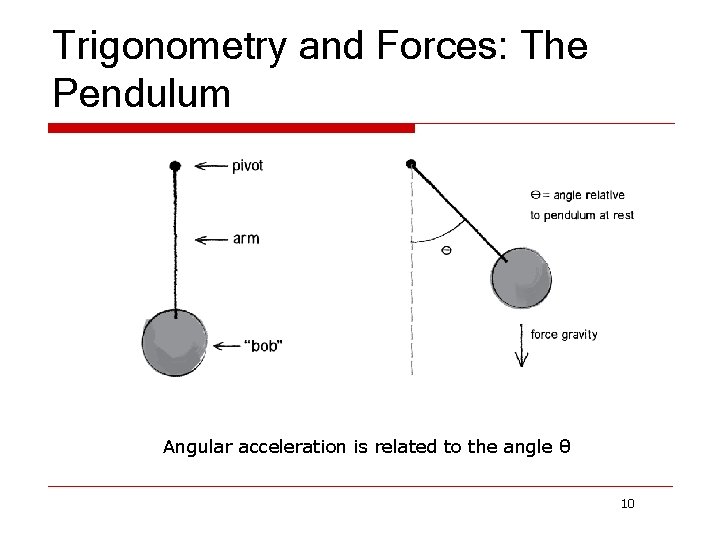
Trigonometry and Forces: The Pendulum Angular acceleration is related to the angle θ 10

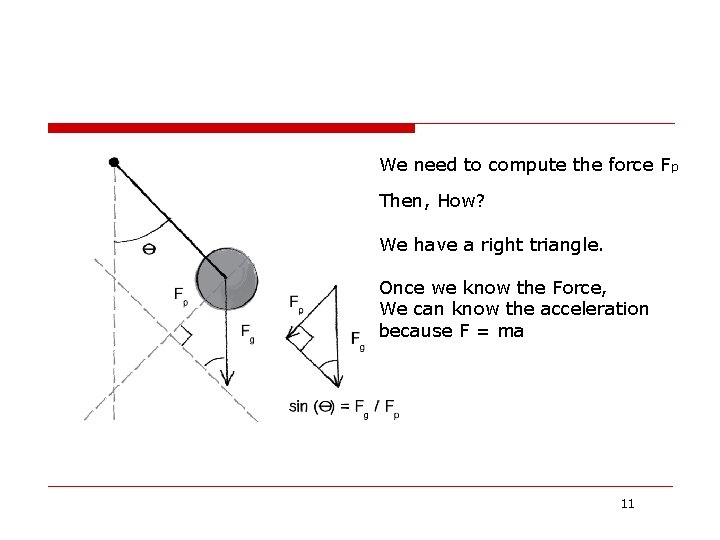
We need to compute the force Fp Then, How? We have a right triangle. Once we know the Force, We can know the acceleration because F = ma 11

Let’s compute the Force o Fp = Fg * sine(θ) o angular velocity = angular velocity + angular acceleration o angle = angle + angular velocity F = ma a=F/ m o pendulum angular acceleration = (acceleration due to gravity * sine (θ))/m o Bob should stop at a point -> Friction effect o How can we simulate Friction? n Simplest way is to put the damping on the angular velocity void update() { float gravity = 0. 4; a. Acceleration = ((-1 * gravity / r) * sin(angle))/mass; a. Velocity += a. Acceleration; a. Velocity *= damping; //damping = 0. 995 angle += a. Velocity; } 12

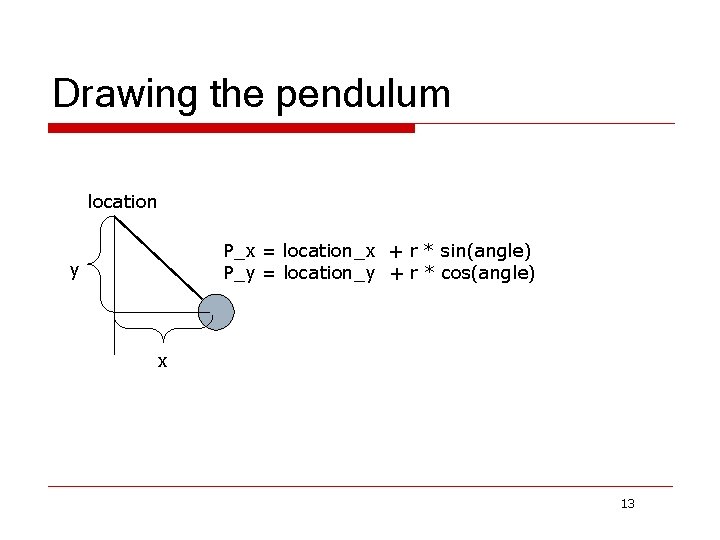
Drawing the pendulum location P_x = location_x + r * sin(angle) P_y = location_y + r * cos(angle) y x 13

Exercise : Let’s make a pendulum – Class design! Pendulum p; void setup() { size(800, 200); smooth(); //position and length PVector position = new PVector(width/2, 0); p = new Pendulum(position, 175); float ballr; float damping; } void draw() { } class Pendulum { float mass; PVector location; // Location of pendulum ball PVector origin; // Location of arm origin float r; // Length of arm float angle; // Pendulum arm angle float a. Velocity; // Angle velocity float a. Acceleration; // Angle acceleration background(255); p. go(); // Ball radius // Arbitary damping amount Pendulum(PVector origin_, float r_) { //initialize the member variables //set the initial angle = PI/4; } void go() { update(); display(); } void update() { //compute the a. Acceleration, a. Velocity, angle } void display() { } } 14

Some hints for the initial values o angle = PI/4; o o o a. Velocity = 0. 0; a. Acceleration = 0. 0; damping = 0. 995; // Arbitrary damping ballr = 48. 0; mass = 1. 0; 15

Exercise : Let’s make a interactive pendulum – Member functions Pendulum p; void setup() { size(800, 200); smooth(); PVector position = new PVector(width/2, 0); p = new Pendulum(position, 175); } void draw() { } background(255); p. go(); void mouse. Pressed() { //pick up the “Bob” p. pick. Up(mouse. X, mouse. Y); } void mouse. Released() { //Unpick the “Bob” p. un. Pick(); } class Pendulum { …… boolean dragging = false; void go() { update(); drag(); //for user interaction display(); } void pick. Up(int mx, int my) { //compute the dist between the bob and mx, my //make dragging = true if it is picked, // otherwise set it to false } void drag() { if (dragging) { //compute the angle based on the mouse position } } void unpick. Up() { dragging = false; } 16

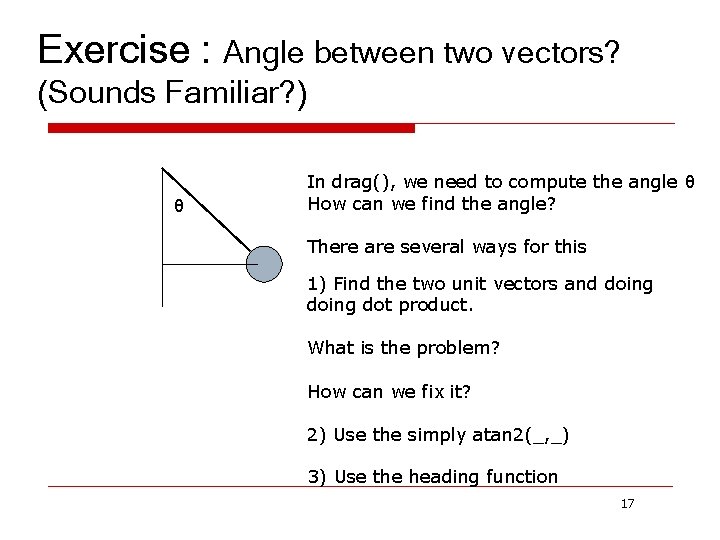
Exercise : Angle between two vectors? (Sounds Familiar? ) θ In drag(), we need to compute the angle θ How can we find the angle? There are several ways for this 1) Find the two unit vectors and doing dot product. What is the problem? How can we fix it? 2) Use the simply atan 2(_, _) 3) Use the heading function 17

Springs 18

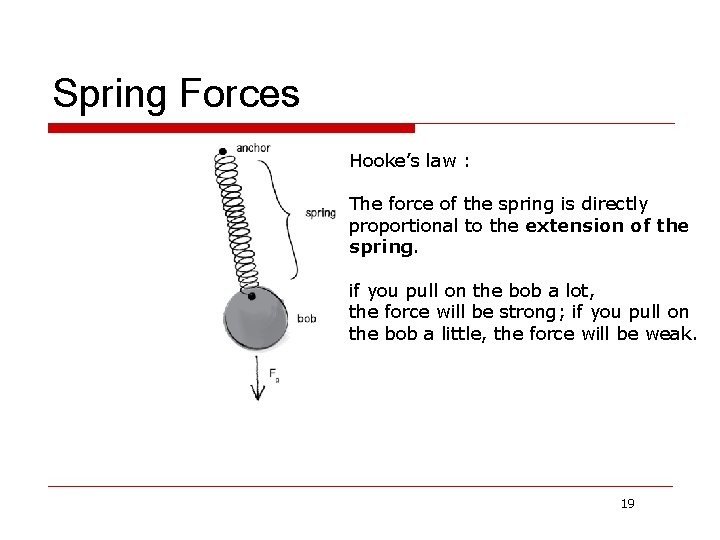
Spring Forces Hooke’s law : The force of the spring is directly proportional to the extension of the spring. if you pull on the bob a lot, the force will be strong; if you pull on the bob a little, the force will be weak. 19

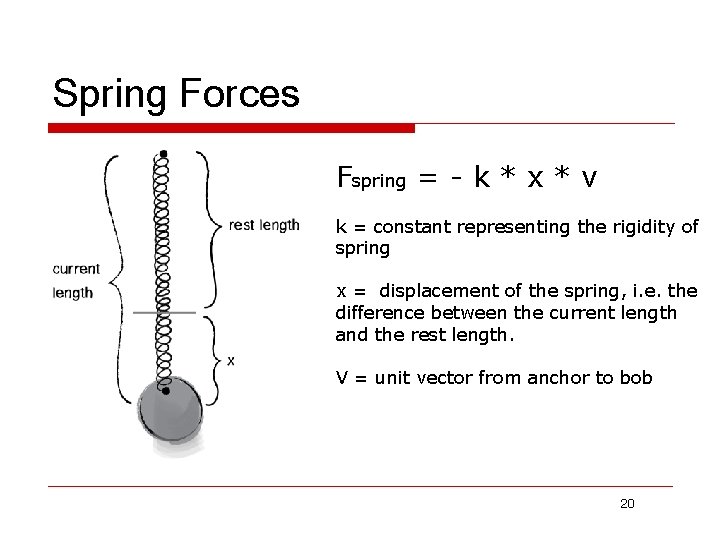
Spring Forces Fspring = - k * x * v k = constant representing the rigidity of spring x = displacement of the spring, i. e. the difference between the current length and the rest length. V = unit vector from anchor to bob 20

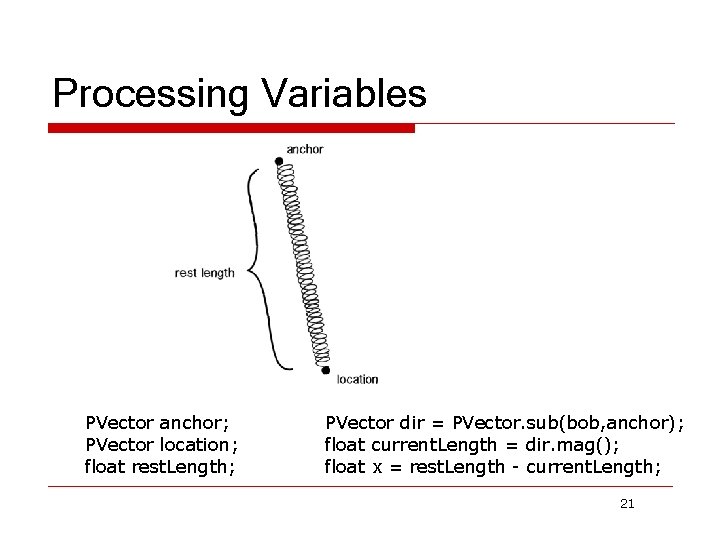
Processing Variables PVector anchor; PVector location; float rest. Length; PVector dir = PVector. sub(bob, anchor); float current. Length = dir. mag(); float x = rest. Length - current. Length; 21

Coding time! o Three classes n Spring n Bob n Spring. Example : Set up window and create instances spring Bob 22

Spring class Spring { // Location PVector anchor; // Rest length and spring constant float len; float k = 0. 2; // Constructor Spring(float x, float y, int l) { anchor = new PVector(x, y); len = l; } // Calculate spring force void connect(Bob b) { //compute the force given b // get the direction vector from the anchor to bob // get the length of direction vector // get the size difference between the length and rest length // calculate the force b. apply. Force(force); } void display() { } } 23

Bob class Bob { PVector location; PVector velocity; PVector acceleration; float mass = 24; float damping = 0. 98; // For mouse interaction boolean dragging = false; // Constructor Bob(float x, float y) { //initialize the member variables } // Standard Euler integration void update() { //update velocity // apply damping on velocity //update location // set acceleration = 0; } void pick. Up(int mx, int my) { float d = dist(mx, my, location. x, location. y); if (d < mass) { dragging = true; } } void stop. Dragging() { dragging = false; } } void drag(int mx, int my) { if (dragging) { location. x = mx; location. y = my; } } // Newton's law: F = M * A void apply. Force(PVector force) { //same code here } // Draw the bob void display() { } 24

Spring Example Class Bob bob; Spring spring; void setup() { spring = new Spring(width/2, 100); bob = new Bob(width/2, 100); } void draw() { PVector gravity = new PVector(0, 1); bob. apply. Force(gravity); spring. connect(bob); bob. update(); bob. drag(mouse. X, mouse. Y); bob. display(); spring. display(); } void mouse. Pressed() { bob. pick. Up(mouse. X, mouse. Y); } void mouse. Released() { bob. un. Pick(); 25